
א. תארו כיצד בנוי פרח השושן בעל שבעה עלי כותרת. כמה מיתרים בשושן זה? (מיתר- קטע שקצותיו על הקף המעגל)

ב. שגיא ניסה לחשב כמה קווים יהיו בשושן בעל 10 עלי כותרת (10 נקודות על המעגל), וטען שמכל נקודה יוצאים 9 מיתרים לכן יהיו ![]() מיתרים בסה"כ. הילה לא הסכימה עמו. היא חישבה
מיתרים בסה"כ. הילה לא הסכימה עמו. היא חישבה ![]() .
.
הסבירו כיצד לדעתכם כל אחד מהם ספר? מי לדעתכם צודק?
ג. כמה מיתרים יש בשושן בעל 100 עלי כותרת?
ד. לפרח השושן המסתורי יש 4851 מיתרים. כמה עלי כותרת יש לו? (כמה נקודות על הקף המעגל?) האם יתכנו פרחים בהם 6214 מיתרים? 3655? 7626? 8656?
מקור:Nrich, Mystic Rose

3. מספרים משולשים
כבר ביוון העתיקה התעניין פיתגורס בקשר בין צורות גיאומטריות ומספרים. פיתגורס סידר אבנים במבנה של משולשים וקרא למספר האבנים מספרים משולשים. (הוא חשב גם על מספרים מרובעים, מחומשים וכדומה).

א. כמה אבנים יהיו במבנה המשולש הבא? כלומר, מהו המספר המשולש החמישי?
ב. הילה ניסתה לחשב כמה אבנים יהיו במשולש ה- 10 וטענה שבכדי לבנות את המשולש העשירי יש להוסיף למשולש התשיעי 10 אבנים. וכך הלאה. ולכן חישבה: ![]()
שגיא מצא שיטה אחרת. הוא טען שאם יכפיל את מספר האבנים יוכל ליצור מבנה מלבני בו יהיה לו קל יותר לחשב. לכן חשב ומצא שבמשולש העשירי יהיו ![]() אבנים בסה"כ.התבוננו ביישום הבא Picturing Triangle Numbers:
אבנים בסה"כ.התבוננו ביישום הבא Picturing Triangle Numbers:
Inline Frames
הסבירו כיצד לדעתכם כל אחד מהם ספר? מי לדעתכם צודק?
ג. כמה אבנים יש במשולש ה- 100?
ד. אחד העוזרים של פיתגורס בנה משולש ובו 4851 אבנים, אך התבלבל בספירה. התוכלו לדעת איזה משולש בנה?
האם יתכנו משולשים בהם 6214 אבנים? 3655? 7626? 8656?
מקור: Nrich, Picturing Triangle Numbers
מספרים פירמידליים, שמואל אביטל, גליונות לחשבון מס 43.קצת על הסתברות, קומבינטוריקה ומספרים משולשים - דוד רץ, על"ה 32.שיבוץ מספרים לפי תכונות - משחק מאת מרכז המורים למתמטיקה ביסודי.לא רק גאוס יכול - בעיית החודש מס 23.לחשוב באופן אלגברי, מעבר לתוכנית הלימודים של ביה"ס היסודי - קאפוט, בלנטון וסוארס - מאמר מתורגם.אותה הגברת בשינוי אדרת - הרצאה של דן עמיר.סדרות, אינדוקציה ונוסחאות נסיגה, הזדמנות לקישוריות בין התחומים במתמטיקה - ד"ר חמוטל דוד, על"ה 32.




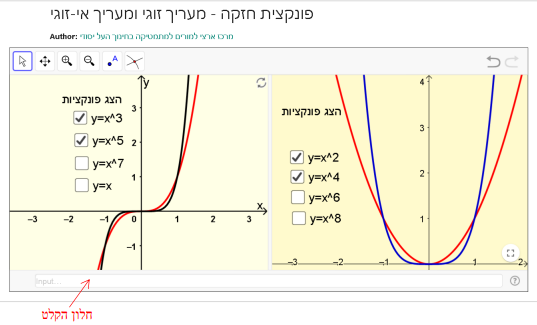
 1. הגרף של פונקציה זוגית
1. הגרף של פונקציה זוגית  1. השטח הצבוע הוא:
1. השטח הצבוע הוא: 


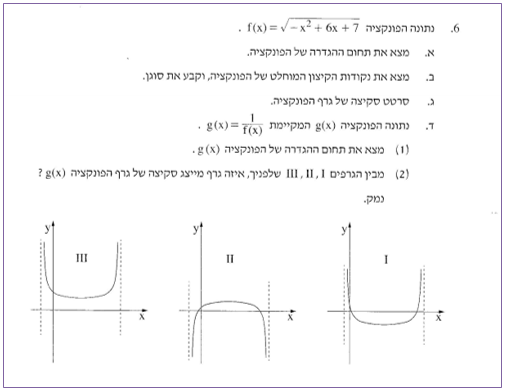
 א. נתון גרף הפונקציה (f(x
א. נתון גרף הפונקציה (f(x







 המרובע
המרובע 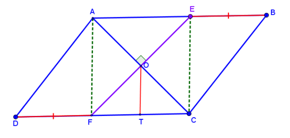 4. נתון גם:
4. נתון גם: 







 נתון משולש ישר זווית
נתון משולש ישר זווית  ב. באותה עת, נצבע משולש ישר זווית חופף '
ב. באותה עת, נצבע משולש ישר זווית חופף '



 (1)
(1)  3. סרטטו מלבן שאחד מקדקודיו הוא ראשית הצירים וקדקוד נגדי לו הוא
3. סרטטו מלבן שאחד מקדקודיו הוא ראשית הצירים וקדקוד נגדי לו הוא 
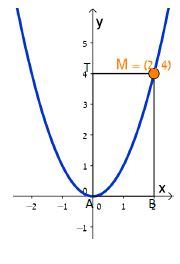
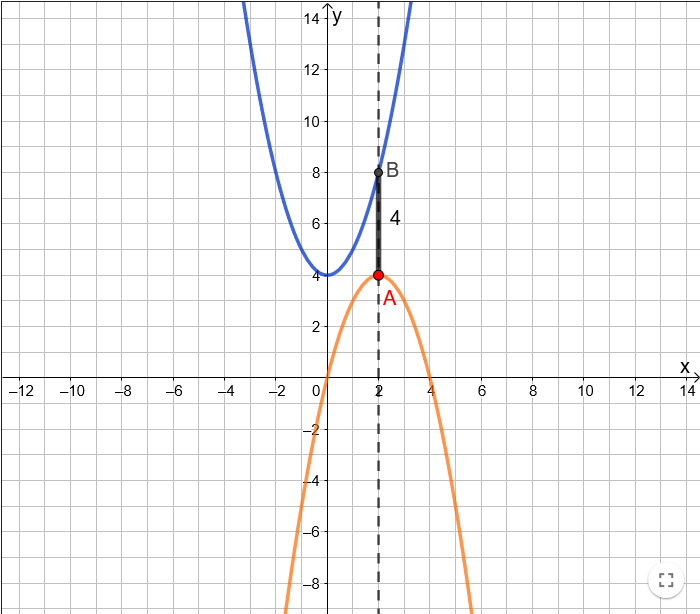
 6. עופר ואלון בנו מלבן שקדקוד אחד שלו על הפרבולה
6. עופר ואלון בנו מלבן שקדקוד אחד שלו על הפרבולה  7. גם יעל בנתה מלבן עבור הפרבולה המוזזת
7. גם יעל בנתה מלבן עבור הפרבולה המוזזת 



 חלק א
חלק א
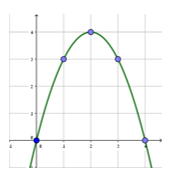

 2. הסבירו מדוע אין אפשרות לקבל ביישומון את צירוף הגרפים הבא:
2. הסבירו מדוע אין אפשרות לקבל ביישומון את צירוף הגרפים הבא: נתון משולש
נתון משולש 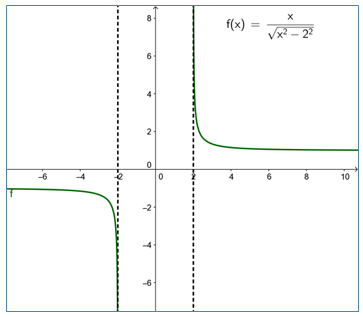 ד. לפניכם אחת הפונקציות מהמשפחה
ד. לפניכם אחת הפונקציות מהמשפחה 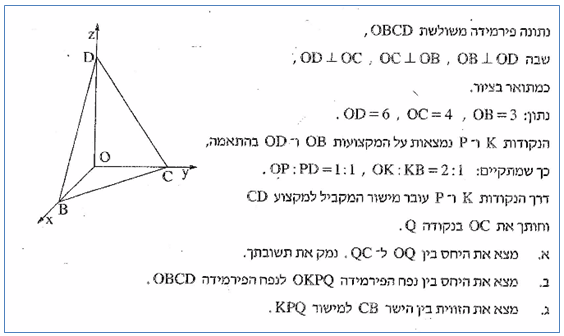






 תקציר
תקציר נעלה בחזקה זוגית או אי זוגית
נעלה בחזקה זוגית או אי זוגית הנקודה
הנקודה  ג. הוסיפו, באמצעות תיבת הבחירה, קטע
ג. הוסיפו, באמצעות תיבת הבחירה, קטע  ד. הוסיפו באמצעות תיבת הבחירה את התיכון
ד. הוסיפו באמצעות תיבת הבחירה את התיכון  ה. דנה המשיכה ושיחקה ביישומון שלנו, וקיבלה את האיור הבא:
ה. דנה המשיכה ושיחקה ביישומון שלנו, וקיבלה את האיור הבא: הפאי הוא מספר מסתורי, המהלך קסם על מתמטיקאים, מדענים וחובבים רבים, ערכו המקורב - 3.14159. ברחבי העולם נוהגים לחגוג לכבודו את יום הפאי ב-14 למרץ (אותו מקובל לרשום כ- 3.14) החל מהשעה 1:59...
הפאי הוא מספר מסתורי, המהלך קסם על מתמטיקאים, מדענים וחובבים רבים, ערכו המקורב - 3.14159. ברחבי העולם נוהגים לחגוג לכבודו את יום הפאי ב-14 למרץ (אותו מקובל לרשום כ- 3.14) החל מהשעה 1:59... פיצוחים בנושא הפאי ויישומו
פיצוחים בנושא הפאי ויישומו  חגיגות יום הפאי
חגיגות יום הפאי 
 ב. עליכם ליצור שני ריבועים, כך שסכום שטחי שני הריבועים יהיה הקטן ביותר.
ב. עליכם ליצור שני ריבועים, כך שסכום שטחי שני הריבועים יהיה הקטן ביותר.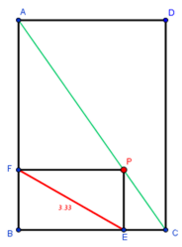 2. השער הקטון
2. השער הקטון 3. שאבתם מים
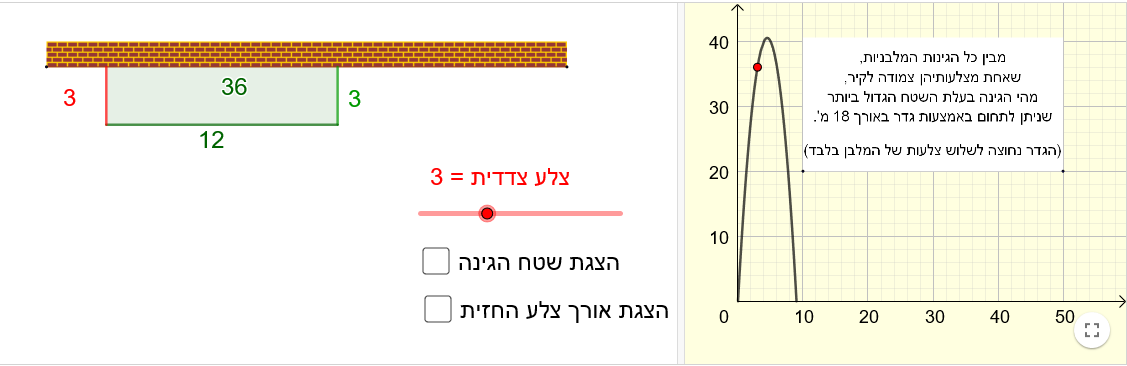
3. שאבתם מים 4. השטח הכי גדול
4. השטח הכי גדול בבית ספרנו חוגגים את יום הפאי במרוץ מסורתי.
בבית ספרנו חוגגים את יום הפאי במרוץ מסורתי. 
 א. אורך המסלול החיצוני הוא 400 מטר.
א. אורך המסלול החיצוני הוא 400 מטר. 














 בשתי דרכים: בחישוב אינטגרל מסוים ובשימוש הנוסחה המהפכנית.
בשתי דרכים: בחישוב אינטגרל מסוים ובשימוש הנוסחה המהפכנית.

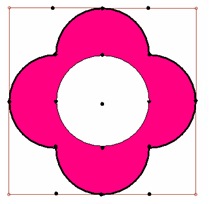


 פרח החיים הוא אחת הצורות בגיאומטריה המקודשת שחוצה תרבויות ויבשות, אולי הפרח טומן בחובו סוד, בנוסף להיותו צורה גיאומטרית יפה ומושלמת.
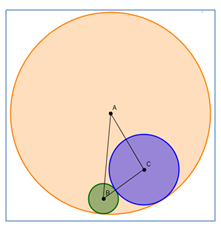
פרח החיים הוא אחת הצורות בגיאומטריה המקודשת שחוצה תרבויות ויבשות, אולי הפרח טומן בחובו סוד, בנוסף להיותו צורה גיאומטרית יפה ומושלמת. בתיבה מלבנית שלושה מטבעות זהב הנוגעים זה בזה, בדומה לאיור (המטבע הגדול נוגע בשלוש צלעותיו של המלבן, הבינוני בשתי צלעותיו והקטן בצלע אחת).
בתיבה מלבנית שלושה מטבעות זהב הנוגעים זה בזה, בדומה לאיור (המטבע הגדול נוגע בשלוש צלעותיו של המלבן, הבינוני בשתי צלעותיו והקטן בצלע אחת). בגליל שקוטרו 2 ס"מ מונחים שלושה מטבעות בדומה לאיור. שני מטבעות ארד בקוטר 1 ס"מ המשיקים זה לזה ומטבע נוסף, מטבע זהב.
בגליל שקוטרו 2 ס"מ מונחים שלושה מטבעות בדומה לאיור. שני מטבעות ארד בקוטר 1 ס"מ המשיקים זה לזה ומטבע נוסף, מטבע זהב.






 שלב 1:
שלב 1: שלב 2:
שלב 2: שלב 3:
שלב 3: שלב 4:
שלב 4:
 טבעת מביוס- עבודת תחריט עץ של האמן אשר
טבעת מביוס- עבודת תחריט עץ של האמן אשר  ראשית, נזכר כיצד בונים את טבעת מביוס. צפו בסרט הוידאו:
ראשית, נזכר כיצד בונים את טבעת מביוס. צפו בסרט הוידאו:
 השנייה...
השנייה... א. מצאו בעזרת האיור את הסכום 1+2+3+4+5+6
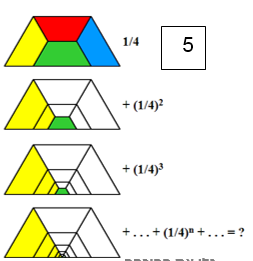
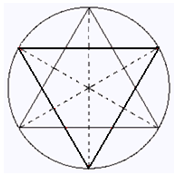
א. מצאו בעזרת האיור את הסכום 1+2+3+4+5+6 א. מהו היחס בין השטח של המשולש הכתום הגדול והמשולש כולו?
א. מהו היחס בין השטח של המשולש הכתום הגדול והמשולש כולו?




 קרול לואיס (מחבר עליסה בארץ הפלאות ) הוכיח שכל המשולשים
קרול לואיס (מחבר עליסה בארץ הפלאות ) הוכיח שכל המשולשים


 1. חשוב "ממוצע אחר"
1. חשוב "ממוצע אחר"
 ב. תארו במילים ובאלגברה את השיטה לחשוב "ממוצע אחר" והוכיחו אותו:
ב. תארו במילים ובאלגברה את השיטה לחשוב "ממוצע אחר" והוכיחו אותו: 2. אי שוויונות בתמונות
2. אי שוויונות בתמונות 
 3. מי גדול ממי?
3. מי גדול ממי?


















 2. הסרט קונטקט ( 1997,Contact)
2. הסרט קונטקט ( 1997,Contact)  א. מחקו את המספר 1 (כי אינו ראשוני)
א. מחקו את המספר 1 (כי אינו ראשוני)


 d= המרחק בין סיינה לאלכסנדריה
d= המרחק בין סיינה לאלכסנדריה
 Eratosthene Sagan
Eratosthene Sagan


 1. מהו רדיוס כדור הארץ?
1. מהו רדיוס כדור הארץ?





 בצעו זאת גם על רביעיות נוספות של מספרים עוקבים.
בצעו זאת גם על רביעיות נוספות של מספרים עוקבים.








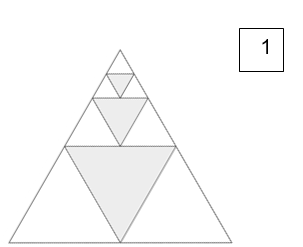
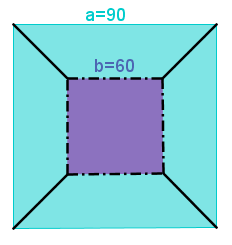
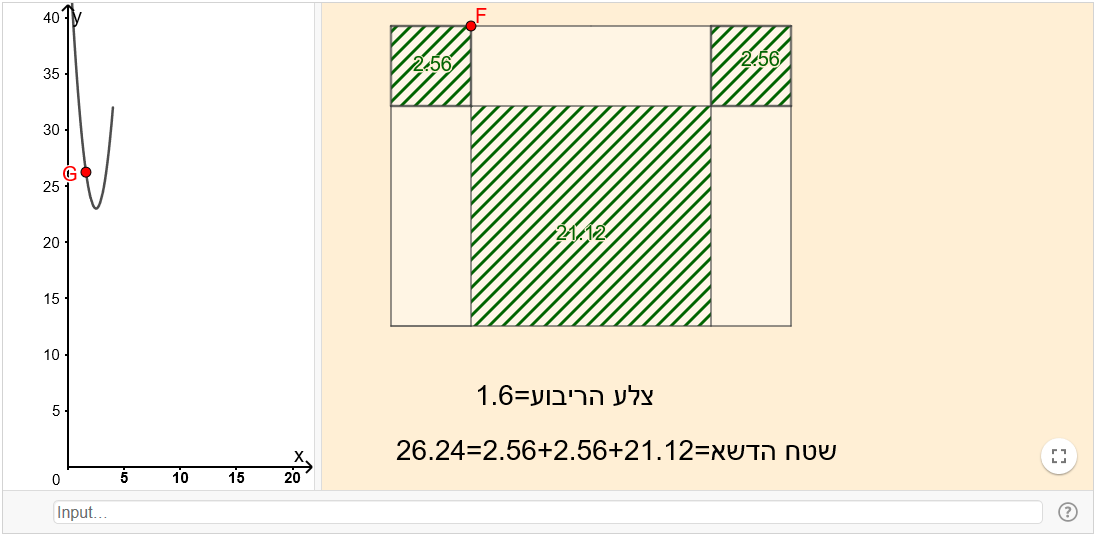
 כיצד ישתנה יחס השטחים כאשר אורך צלע הריבוע הצהוב הוא באורך כלשהו, לאו דווקא שליש צלע הריבוע החיצוני ?
כיצד ישתנה יחס השטחים כאשר אורך צלע הריבוע הצהוב הוא באורך כלשהו, לאו דווקא שליש צלע הריבוע החיצוני ? 3. לקינוח- שוקולד גיאומטרי
3. לקינוח- שוקולד גיאומטרי ג. שאלה למחשבה-
ג. שאלה למחשבה- 1. סביבון מתמטי - סוב סוב סוב !
1. סביבון מתמטי - סוב סוב סוב !

 2. סופגניות חמות ומתוקות
2. סופגניות חמות ומתוקות 3. הנרות הללו
3. הנרות הללו  1. משחק הסופגניות
1. משחק הסופגניות 2. משחק הסביבונים
2. משחק הסביבונים 3. דמי חנוכה
3. דמי חנוכה 1. ללא מילים
1. ללא מילים
 2. הזבוב הטורדן
2. הזבוב הטורדן 3. האיור המתכנס
3. האיור המתכנס 4. לוח מטרה גיאומטרי
4. לוח מטרה גיאומטרי ארכימדס (287- 212 לפנה"ס) היה מדען יווני שהגיע לתוצאות מרשימות במתמטיקה, הנדסה ופיסיקה.
ארכימדס (287- 212 לפנה"ס) היה מדען יווני שהגיע לתוצאות מרשימות במתמטיקה, הנדסה ופיסיקה. 1. שרשרת הזהב של המלך
1. שרשרת הזהב של המלך 2. סכין הסנדלרים
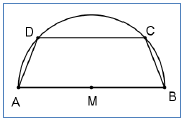
2. סכין הסנדלרים ג. משיק לשני חצאי המעגלים חותך את חצי המעגל הגדול בנקודה D.
ג. משיק לשני חצאי המעגלים חותך את חצי המעגל הגדול בנקודה D.  למתעניינים - התנסו בפרויקט "
למתעניינים - התנסו בפרויקט "








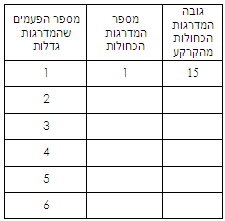
 מגרש בית הספר בנוי ממלבן עליו בנויים שני חצאי מעגלים. המגרש מכיל ששה מסלולי ריצה כל מסלול ברוחב של מטר אחד.
מגרש בית הספר בנוי ממלבן עליו בנויים שני חצאי מעגלים. המגרש מכיל ששה מסלולי ריצה כל מסלול ברוחב של מטר אחד.















 1. האוצר
1. האוצר

 2. במגרש הכדורסל
2. במגרש הכדורסל  עליכם לתכנן תפריט לארוחת בקר בריאה שתכיל לכל היותר 500 קלוריות, ע"פ הטבלה הבאה:
עליכם לתכנן תפריט לארוחת בקר בריאה שתכיל לכל היותר 500 קלוריות, ע"פ הטבלה הבאה:

















 2. עבודה בחופשת הקיץ
2. עבודה בחופשת הקיץ  4. אימון כושר ושריפת קלוריות
4. אימון כושר ושריפת קלוריות 1. גינת השושנים
1. גינת השושנים 





 חידה 1
חידה 1 חידה 2
חידה 2





























































 1. זהויות טריגונומטריות לסכום זוויות
1. זהויות טריגונומטריות לסכום זוויות 2. זהויות טריגונומטריות לזווית כפולה
2. זהויות טריגונומטריות לזווית כפולה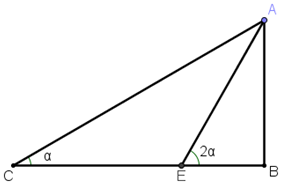 3. עוד זהויות טריגונומטריות לזווית כפולה
3. עוד זהויות טריגונומטריות לזווית כפולה 
















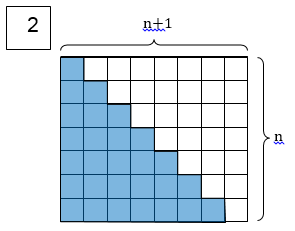
 א. הסבירו ע"פ האיור, או בדרך אחרת, מדוע עבור כל n טבעי n2)-n) מתחלק ב- 2.
א. הסבירו ע"פ האיור, או בדרך אחרת, מדוע עבור כל n טבעי n2)-n) מתחלק ב- 2.


























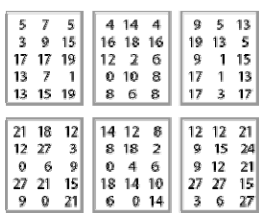
 1. גלו את המספר שבמשבצת הריקה
1. גלו את המספר שבמשבצת הריקה 2. האם יש רמזים עודפים?
2. האם יש רמזים עודפים? 3. בדרך שלהם
3. בדרך שלהם 4. האם הרמזים מספיקים?
4. האם הרמזים מספיקים? 5. הפינה לשיפוטיכם
5. הפינה לשיפוטיכם ב. לכל אחת מן המשוואות הבאות קבעו את מספר הפתרונות.
ב. לכל אחת מן המשוואות הבאות קבעו את מספר הפתרונות. 7. שומרי משקל
7. שומרי משקל
 שירה: אריק איינשטיין
שירה: אריק איינשטיין
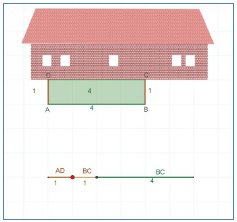
 ח. הגמד הגדיל את ביתו פי 2, אך החליט לשנות את הצלעות של הגג האדום בבית הענקים כך שהשוקיים של משולש הגג החדש יהיו באותו גודל של בסיס המשולש. (ראו ציור) האם עדיין המבנה, הגג והדלת יהיו דומים זה לזה?
ח. הגמד הגדיל את ביתו פי 2, אך החליט לשנות את הצלעות של הגג האדום בבית הענקים כך שהשוקיים של משולש הגג החדש יהיו באותו גודל של בסיס המשולש. (ראו ציור) האם עדיין המבנה, הגג והדלת יהיו דומים זה לזה? זוכרים את
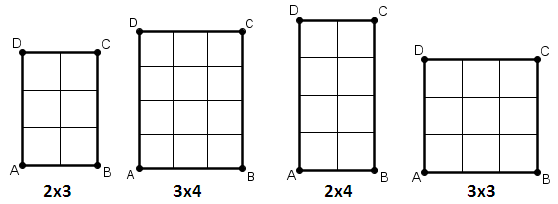
זוכרים את  א. כמה מלבנים יש לדעתכם בציור?
א. כמה מלבנים יש לדעתכם בציור? 










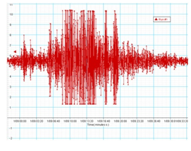
 אחד התחומים שעניינו במיוחד את נאפייר היתה האסטרונומיה, אך המחשבה על החישובים האינסופיים הנדרשים מאסטרונומים גרמה לו לאנחות. לאחר 20 שנות לימוד וניסויים, הציג נאפייר את השימוש בלוגריתמים - פריצת דרך שלא תאמן בפישוט החישוב. תגלית זו התקבלה בכל רחבי העולם בתרועה ובהסכמה, לא רק על ידי אסטרונומים, אלא גם על ידי אנשים שחישובים מגושמים הכבידו עליהם. לוגריתמים, העיקרון שעליו מבוסס סרגל החישוב, ביטלו למעשה את הצורך בכפל וחילוק ואפשרו להסתפק בחיבור וחיסור.
אחד התחומים שעניינו במיוחד את נאפייר היתה האסטרונומיה, אך המחשבה על החישובים האינסופיים הנדרשים מאסטרונומים גרמה לו לאנחות. לאחר 20 שנות לימוד וניסויים, הציג נאפייר את השימוש בלוגריתמים - פריצת דרך שלא תאמן בפישוט החישוב. תגלית זו התקבלה בכל רחבי העולם בתרועה ובהסכמה, לא רק על ידי אסטרונומים, אלא גם על ידי אנשים שחישובים מגושמים הכבידו עליהם. לוגריתמים, העיקרון שעליו מבוסס סרגל החישוב, ביטלו למעשה את הצורך בכפל וחילוק ואפשרו להסתפק בחיבור וחיסור.






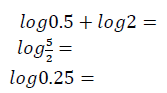










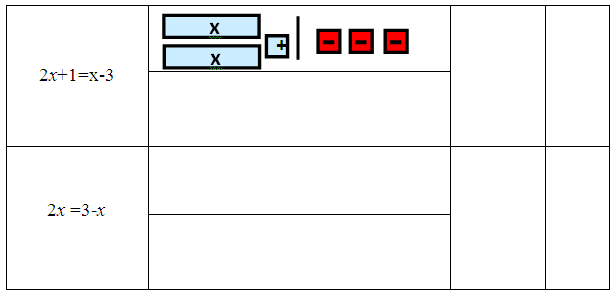
 בארץ יצורי הפרא המתמטיים חיים יחדיו שני סוגי יצורים:
בארץ יצורי הפרא המתמטיים חיים יחדיו שני סוגי יצורים: יצורי הפרא הזמינו לארצם שני יצורים נוספים, יצורי x, אשר יסייעו להם לפתור משוואות.
יצורי הפרא הזמינו לארצם שני יצורים נוספים, יצורי x, אשר יסייעו להם לפתור משוואות. 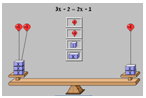























 א. המשחק "השלימו לריבוע"
א. המשחק "השלימו לריבוע"




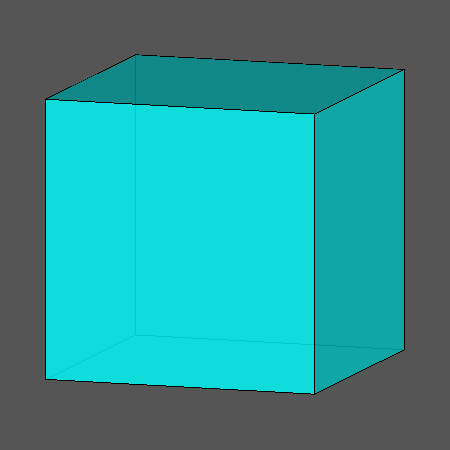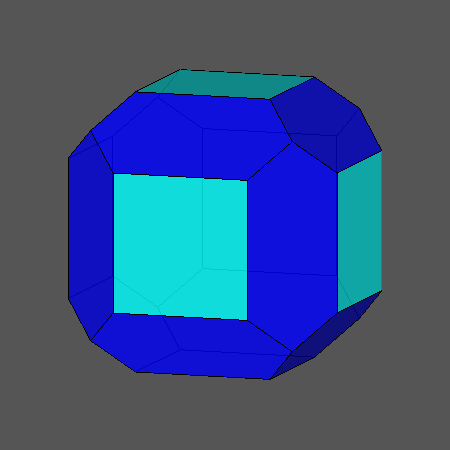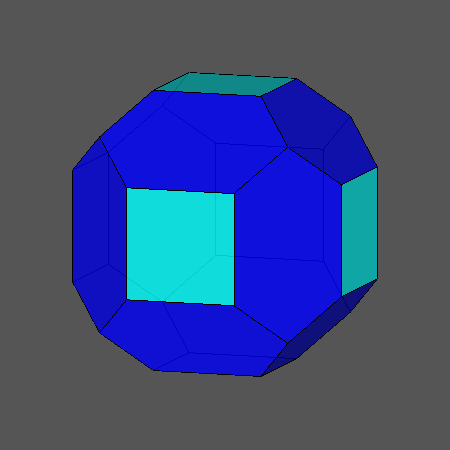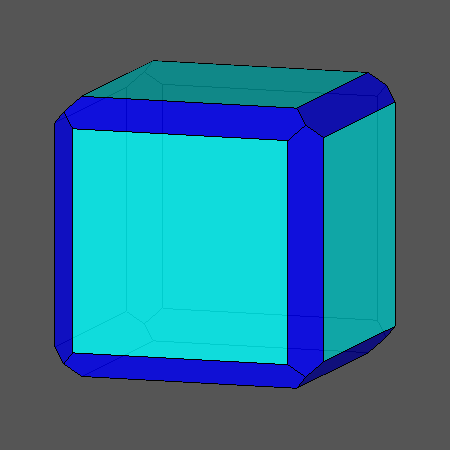

 המפורסם שבהם הוא העשרימון הקטום, הוא הכדורגל. קראו מאמר באלף אפס בנושא,
המפורסם שבהם הוא העשרימון הקטום, הוא הכדורגל. קראו מאמר באלף אפס בנושא, 



 על פני קופסת מתנה בצורת קוביה שאורך מקצועה 10 ס"מ,
על פני קופסת מתנה בצורת קוביה שאורך מקצועה 10 ס"מ,  מהפינה של קוביית חימר (או פלסטלינה) שאורך מקצועה 10 ס"מ, נחתך חתך מישורי בצורת משולש שווה צלעות. (ראו איור)
מהפינה של קוביית חימר (או פלסטלינה) שאורך מקצועה 10 ס"מ, נחתך חתך מישורי בצורת משולש שווה צלעות. (ראו איור) צרו קובייה מחימר או פלסטלינה. בעזרת חוט ניילון חתכו את הקובייה לשניים.
צרו קובייה מחימר או פלסטלינה. בעזרת חוט ניילון חתכו את הקובייה לשניים.  אריזת מתנה בצורת תיבה נעטפה בנייר אריזה, כך ששטח הפאות של התיבה הוא: 3 סמ"ר, 12 סמ"ר ו-25 ס"מר.
אריזת מתנה בצורת תיבה נעטפה בנייר אריזה, כך ששטח הפאות של התיבה הוא: 3 סמ"ר, 12 סמ"ר ו-25 ס"מר. כדור טניס בקוטר 10 ס"מ נארז בקובייה התגלגל לפינה.
כדור טניס בקוטר 10 ס"מ נארז בקובייה התגלגל לפינה. נמלה עמלנית יצאה לטייל על פני חרוט, שמידותיו מתוארות בציור, במטרה להגיע מנקודה A לנקודה B.
נמלה עמלנית יצאה לטייל על פני חרוט, שמידותיו מתוארות בציור, במטרה להגיע מנקודה A לנקודה B. 4. הקובייה שבפנים
4. הקובייה שבפנים הריבוע האדום מסתובב סביב מרכז הריבוע הכחול, כך שאחד מקודקודי הריבוע האדום מונח במרכזו של הריבוע הכחול. ראו את
הריבוע האדום מסתובב סביב מרכז הריבוע הכחול, כך שאחד מקודקודי הריבוע האדום מונח במרכזו של הריבוע הכחול. ראו את 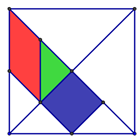 במשחק טנגרם
במשחק טנגרם
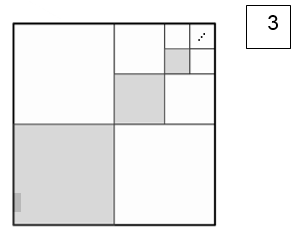
 א. על כל אחת מצלעות ריבוע שאורך צלעו יחידה, הקצו נקודת אמצע, ויצרו ריבוע פנימי. (ראו איור)
א. על כל אחת מצלעות ריבוע שאורך צלעו יחידה, הקצו נקודת אמצע, ויצרו ריבוע פנימי. (ראו איור) ג. שנו את האיור
ג. שנו את האיור 
 4. שטחים בריבוע
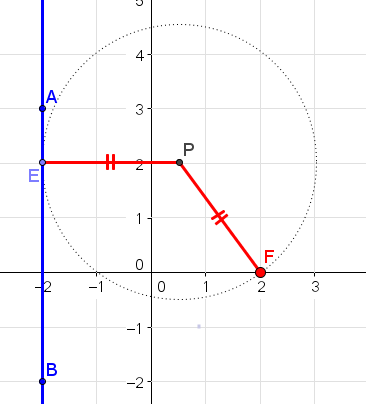
4. שטחים בריבוע א. היכן לדעתכם יש למקם את הנקודה P כך שהחלוקה תהיה הוגנת? מדוע?
א. היכן לדעתכם יש למקם את הנקודה P כך שהחלוקה תהיה הוגנת? מדוע? נתונה תיבה מלבנית ובתוכה נלכד עכביש בנקודה P שהיא מרכז התיבה. העכביש מתח חוטים לפינות התיבה כך שיצר פירמידות אשר קודקוד הראש שלהן הנקודה P ובסיסן פאות
נתונה תיבה מלבנית ובתוכה נלכד עכביש בנקודה P שהיא מרכז התיבה. העכביש מתח חוטים לפינות התיבה כך שיצר פירמידות אשר קודקוד הראש שלהן הנקודה P ובסיסן פאות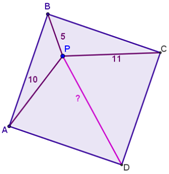
 ב. כיצד ישתנה המרחק PD כאשר המגרש יהיה מלבני?
ב. כיצד ישתנה המרחק PD כאשר המגרש יהיה מלבני? ג. מה יהיה המרחק PD אם השחקן יהיה מחוץ למגרש?
ג. מה יהיה המרחק PD אם השחקן יהיה מחוץ למגרש? ד. מה יהיה המרחק PD אם נתון כי: PB=a ,PA=c ,PC=b?
ד. מה יהיה המרחק PD אם נתון כי: PB=a ,PA=c ,PC=b? נתונה תיבה ובתוכה נלכד עכביש בנקודה P. העכביש מתח חוטים לפינות התיבה כך ש:
נתונה תיבה ובתוכה נלכד עכביש בנקודה P. העכביש מתח חוטים לפינות התיבה כך ש: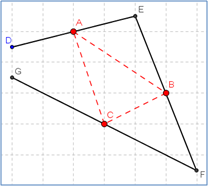 - האם תמיד ניתן לבנות את המשולש על פי אמצעי צלעותיו?
- האם תמיד ניתן לבנות את המשולש על פי אמצעי צלעותיו? - האם תמיד ניתן לבנות את המרובע על פי אמצעי צלעותיו? אם כן, באיזה תנאי?
- האם תמיד ניתן לבנות את המרובע על פי אמצעי צלעותיו? אם כן, באיזה תנאי? בפיצוח זה נשרטט ונתבונן בעין מתמטית בפרחים המרהיבים הללו, בעלי שישה עלי כותרת.
בפיצוח זה נשרטט ונתבונן בעין מתמטית בפרחים המרהיבים הללו, בעלי שישה עלי כותרת. ב. שני משושים בפרח
ב. שני משושים בפרח
 ברדיאנים:
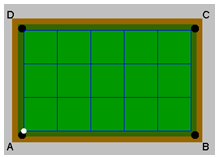
ברדיאנים:  א. בשכונת "על כנפי הדמיון" הוקם גן משחקים חדש ובו מתקני ספורט ואתגרים. הגן בנוי מרצף של שלשה מתחמים ריבועיים. המרחק בין שתי הפינות המנוגדות של הגן הוא 100 מטר (ראו בשרטוט AD). אדריכל הגן תכנן לשתול ארבעה עצים שיפרשו צל בגן בנקודות: A, B, C ו-D (ראו איור).
א. בשכונת "על כנפי הדמיון" הוקם גן משחקים חדש ובו מתקני ספורט ואתגרים. הגן בנוי מרצף של שלשה מתחמים ריבועיים. המרחק בין שתי הפינות המנוגדות של הגן הוא 100 מטר (ראו בשרטוט AD). אדריכל הגן תכנן לשתול ארבעה עצים שיפרשו צל בגן בנקודות: A, B, C ו-D (ראו איור). ב. בשלב ב של הקמת הגן, הורחב המגרש לשישה מתחמים ריבועיים. אדריכל הגן תכנן להוסיף ולשתול ארבעה עצים שיפרשו צל בגן בנקודות: E, F, G ו-H (ראו איור).
ב. בשלב ב של הקמת הגן, הורחב המגרש לשישה מתחמים ריבועיים. אדריכל הגן תכנן להוסיף ולשתול ארבעה עצים שיפרשו צל בגן בנקודות: E, F, G ו-H (ראו איור). ג. עץ נוסף נשתל בנקודה K (ראו איור).
ג. עץ נוסף נשתל בנקודה K (ראו איור). ד. הגנן פרש חבלים במתחם הגן על פי הוראות האדריכל. הוא היה מעוניין לחשב את הזווית שנוצרה בקודקוד B. מצאו את הזווית.
ד. הגנן פרש חבלים במתחם הגן על פי הוראות האדריכל. הוא היה מעוניין לחשב את הזווית שנוצרה בקודקוד B. מצאו את הזווית.









 1. סידור המטבעות
1. סידור המטבעות 2. עיגולים על עיגולים
2. עיגולים על עיגולים 3. סבך הנחשים הצבעוניים
3. סבך הנחשים הצבעוניים תלמיד א: נצרף למשולש שלנו משולש נוסף, צירוף הזויות של שני המשולשים נותן זויות של מרובע לכן סכומן 3600, לכן לכל משולש 1800.
תלמיד א: נצרף למשולש שלנו משולש נוסף, צירוף הזויות של שני המשולשים נותן זויות של מרובע לכן סכומן 3600, לכן לכל משולש 1800. תלמיד ב: ההוכחה אינה טובה. מה מבטיח לנו ש- 360 המעלות מתחלקות בשווה בין שני המשולשים?
תלמיד ב: ההוכחה אינה טובה. מה מבטיח לנו ש- 360 המעלות מתחלקות בשווה בין שני המשולשים?  תלמיד ג: יש לי משהו יותר פשוט. נהפוך את המשולש למרובע על-ידי הוספת קדקוד על אחת הצלעות. בקדקוד זה 180o לכן בשאר הקדקודים יחד יש 180o .
תלמיד ג: יש לי משהו יותר פשוט. נהפוך את המשולש למרובע על-ידי הוספת קדקוד על אחת הצלעות. בקדקוד זה 180o לכן בשאר הקדקודים יחד יש 180o . א. לפניכם פירמידה בה הוכנסו בשורה הראשונה המספרים: 2, 1, 4, 6
א. לפניכם פירמידה בה הוכנסו בשורה הראשונה המספרים: 2, 1, 4, 6 ה. לפירמידה הבאה הוכנסו לשורה הראשונה המספרים: -5, 2, 3, 4. באיזה סדר הוכנסו המספרים כך שבפיסגה יתקבל המספר אפס?
ה. לפירמידה הבאה הוכנסו לשורה הראשונה המספרים: -5, 2, 3, 4. באיזה סדר הוכנסו המספרים כך שבפיסגה יתקבל המספר אפס? ו. לפירמידה הבאה הוכנסו בשורה הראשונה המספרים: 2 ו-15 ועוד שני מספרים כלשהם. בראש הפירמידה התקבל המספר 48. מצאו את הקשר בין x ו-y . כמה פירמידות ניתן לקבל?
ו. לפירמידה הבאה הוכנסו בשורה הראשונה המספרים: 2 ו-15 ועוד שני מספרים כלשהם. בראש הפירמידה התקבל המספר 48. מצאו את הקשר בין x ו-y . כמה פירמידות ניתן לקבל? רשמו מספר שלם כלשהו בפינה השמאלית של השורה התחתונה של הפירמידה.
רשמו מספר שלם כלשהו בפינה השמאלית של השורה התחתונה של הפירמידה. א. כל אחת מהצורות A-H הבאות מורכבות מחמישה ריבועים ושני מלבנים. רק מחלקן ניתן לקפל לפי הקווים המקווקווים, ולבנות קובייה 1x1x1, ואילו מחלק מהצורות לא ניתן לבנות קובייה. התוכלו לזהות את הקוביות?
א. כל אחת מהצורות A-H הבאות מורכבות מחמישה ריבועים ושני מלבנים. רק מחלקן ניתן לקפל לפי הקווים המקווקווים, ולבנות קובייה 1x1x1, ואילו מחלק מהצורות לא ניתן לבנות קובייה. התוכלו לזהות את הקוביות? ב. כל אחת מהצורות A-H הבאות מורכבות מחמישה ריבועים ושני משולשים. רק מחלק ן ניתן לקפל לפי הקווים המקווקווים, ולבנות קובייה 1x1x1, ואילו מחלק מהצורות לא ניתן לבנות קובייה. התוכלו לזהות את הקוביות?
ב. כל אחת מהצורות A-H הבאות מורכבות מחמישה ריבועים ושני משולשים. רק מחלק ן ניתן לקפל לפי הקווים המקווקווים, ולבנות קובייה 1x1x1, ואילו מחלק מהצורות לא ניתן לבנות קובייה. התוכלו לזהות את הקוביות?







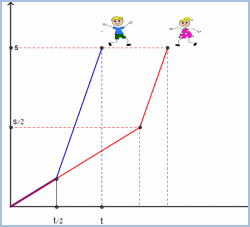
 1. שני חברים יצאו לדרך, בים בם בום....
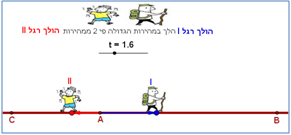
1. שני חברים יצאו לדרך, בים בם בום....  2. ארבעה כלי רכב יצאו לדרך
2. ארבעה כלי רכב יצאו לדרך  3. חידת הנזיר
3. חידת הנזיר  האגדה מספרת שפיתגורס, המתמטיקאי היווני הנודע מימי יוון הקדומה ( 500 לפנה"ס), עבר פעם ליד חרש ברזל והתאהב בצלילי דפיקות הפטיש שהיו נעימים לאוזנו. הוא בדק ומצא, כי משקלי הפטישים היו 6, 8, 9, ו-12 ק"ג. היחסים בין משקלי הפטישים הפיקו צלילים הרמוניים.
האגדה מספרת שפיתגורס, המתמטיקאי היווני הנודע מימי יוון הקדומה ( 500 לפנה"ס), עבר פעם ליד חרש ברזל והתאהב בצלילי דפיקות הפטיש שהיו נעימים לאוזנו. הוא בדק ומצא, כי משקלי הפטישים היו 6, 8, 9, ו-12 ק"ג. היחסים בין משקלי הפטישים הפיקו צלילים הרמוניים.





 ב. הסבירו על פי האיור הבא מדוע הממוצע החשבוני גדול מן הממוצע הגיאומטרי.
ב. הסבירו על פי האיור הבא מדוע הממוצע החשבוני גדול מן הממוצע הגיאומטרי. ג. הסבירו על פי
ג. הסבירו על פי 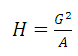
 ה. הוכיחו באיור כי:
ה. הוכיחו באיור כי: 
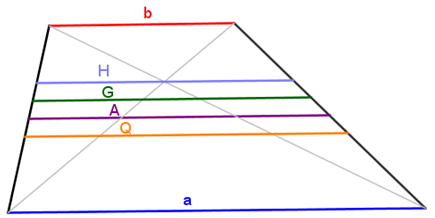 4. ארבעה ממוצעים בטרפז
4. ארבעה ממוצעים בטרפז קפלו דף מלבני לאורכו ולרוחבו כך שיתקבלו בפתיחת הדף ארבעה מלבנים חופפים (ראו איור) כעת סמנו על כל קטע מארבעת הקטעים שהתקבלו (הקיפולים) נקודה כלשהי, וחברו את הנקודות כך שיתקבל מרובע.
קפלו דף מלבני לאורכו ולרוחבו כך שיתקבלו בפתיחת הדף ארבעה מלבנים חופפים (ראו איור) כעת סמנו על כל קטע מארבעת הקטעים שהתקבלו (הקיפולים) נקודה כלשהי, וחברו את הנקודות כך שיתקבל מרובע. 2. נמצא את שטח המרובע שאלכסוניו מאונכים בעזרת קיפולי נייר.
2. נמצא את שטח המרובע שאלכסוניו מאונכים בעזרת קיפולי נייר. 

 1. הזיזו את נקודות Q ו-P
1. הזיזו את נקודות Q ו-P  3. ברשותכם נייר מדפסת A4 (אשר יחס צלעות המלבן שלו הן
3. ברשותכם נייר מדפסת A4 (אשר יחס צלעות המלבן שלו הן  )
) .
.




 ?
?
 .
. ? כמה פתרונות ממשיים שונים?
? כמה פתרונות ממשיים שונים? 
 .
. ?
?  .
. . מה ניתן לומר על שני השורשים המרוכבים ועל מיקומם ביחס לציר הסימטריה?
. מה ניתן לומר על שני השורשים המרוכבים ועל מיקומם ביחס לציר הסימטריה?  .
. .
.  . הוכיחו אלגברית.
. הוכיחו אלגברית. . הוכיחו אלגברית.
. הוכיחו אלגברית.

 .
. ואת שורשי משוואת הפרבולה האחות, בעזרת a,k,p. הוכיחו באופן אלגברי את הקשר בין השורשים.
ואת שורשי משוואת הפרבולה האחות, בעזרת a,k,p. הוכיחו באופן אלגברי את הקשר בין השורשים. הידעתם?
הידעתם?

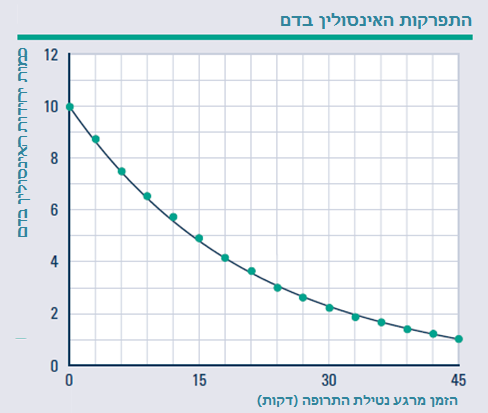
 התפלגות נורמלית, הנקראת גם התפלגות גאוס או עקומת הפעמון, הנה בלי ספק צורת ההתפלגות השימושית ביותר בכל תחומי המדע, החל מסטטיסטיקה, דרך ביולוגיה ועד מדעי החברה. בהתפלגות זו ניתן להשתמש לתיאור הפילוג של תוצאות ניסוי, התפלגות ממוצע ציונים בכיתה, התפלגות מנת המשכל במדגם אוכלוסייה, התפלגות מחיר של מניה ועוד ועוד . קראו על עקומת הפעמון ב
התפלגות נורמלית, הנקראת גם התפלגות גאוס או עקומת הפעמון, הנה בלי ספק צורת ההתפלגות השימושית ביותר בכל תחומי המדע, החל מסטטיסטיקה, דרך ביולוגיה ועד מדעי החברה. בהתפלגות זו ניתן להשתמש לתיאור הפילוג של תוצאות ניסוי, התפלגות ממוצע ציונים בכיתה, התפלגות מנת המשכל במדגם אוכלוסייה, התפלגות מחיר של מניה ועוד ועוד . קראו על עקומת הפעמון ב א. נתבונן בלוח גלטון מוקטן , בעל שתי שורות בלבד. ברור שלכדור הנופל יש שתי אפשרויות בלבד בדרכו, שמאלה (L) או ימינה (R). מהי ההסתברות שיגיע לתא השמאלי?
א. נתבונן בלוח גלטון מוקטן , בעל שתי שורות בלבד. ברור שלכדור הנופל יש שתי אפשרויות בלבד בדרכו, שמאלה (L) או ימינה (R). מהי ההסתברות שיגיע לתא השמאלי? ב. נוסיף שורה ללוח גלטון.
ב. נוסיף שורה ללוח גלטון.




 3. כובע ליצן
3. כובע ליצן

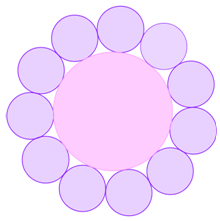 לפניכם פרח עם 12 עלי כותרת. חשבו את היחס בין הרדיוס של המעגל הפנימי לבין רדיוס המעגל החיצוני.
לפניכם פרח עם 12 עלי כותרת. חשבו את היחס בין הרדיוס של המעגל הפנימי לבין רדיוס המעגל החיצוני.
 יישומים דינאמיים - משפטים ובעיות בנושא
יישומים דינאמיים - משפטים ובעיות בנושא  חידת סנגקו בגאוגברה
חידת סנגקו בגאוגברה


 1. במרכז שדה ריבועי 5x5 מ"ר, קשורה בחבל עז רעבתנית, האוכלת כל עשב הנקרה בדרכה.
1. במרכז שדה ריבועי 5x5 מ"ר, קשורה בחבל עז רעבתנית, האוכלת כל עשב הנקרה בדרכה. 2. בתוך שדה רחב נמצא שטח מרוצף ריבועי שאורך צלעו 2 מטר. אל קצות השטח קשורה עז בלולאה בחבל באורך 1 מטר.
2. בתוך שדה רחב נמצא שטח מרוצף ריבועי שאורך צלעו 2 מטר. אל קצות השטח קשורה עז בלולאה בחבל באורך 1 מטר.  3. במרכז שדה נמצא שטח מגודר מלבני ומרוצף בגודל 4x6 מ"ר. עז רעבתנית קשורה האחת הנקודות על הצלע CD.
3. במרכז שדה נמצא שטח מגודר מלבני ומרוצף בגודל 4x6 מ"ר. עז רעבתנית קשורה האחת הנקודות על הצלע CD. 


 א. הנקודה E היא נקודה כלשהי על אלכסון המלבן ABCD. מעבירים מהנקודה E קטעים המקבילים לצלעות המלבן.
א. הנקודה E היא נקודה כלשהי על אלכסון המלבן ABCD. מעבירים מהנקודה E קטעים המקבילים לצלעות המלבן. ד. פתחו את עקרון "משני הצדדים" גם עבור מקבילית.
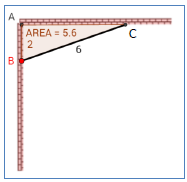
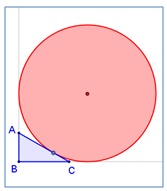
ד. פתחו את עקרון "משני הצדדים" גם עבור מקבילית.  כיצד נמדוד את גובהו של צוק הררי בלב ים ?
כיצד נמדוד את גובהו של צוק הררי בלב ים ?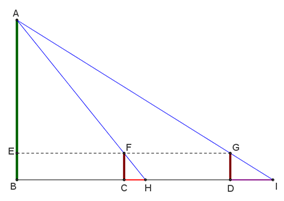 א. השלימו את משולש AHI למקבילית. העבירו מהנקודה G שעל אלכסון המקבילית, מקבילים לצלעות. סמנו את המשולשים הדומים שהתקבלו.
א. השלימו את משולש AHI למקבילית. העבירו מהנקודה G שעל אלכסון המקבילית, מקבילים לצלעות. סמנו את המשולשים הדומים שהתקבלו.
 1. קופסת דגנים של 500 גרם עולה 25 ש"ח.
1. קופסת דגנים של 500 גרם עולה 25 ש"ח. 2. קופסת מיץ תפוזים של 250 מ"ל עולה 5 ₪.
2. קופסת מיץ תפוזים של 250 מ"ל עולה 5 ₪. 3. חפיסת שוקולד של 100 גרם עולה 10 ש"ח.
3. חפיסת שוקולד של 100 גרם עולה 10 ש"ח.


 2. העפיפון
2. העפיפון










 שחר וטל הקימו דוכן כדי למכור לימונדה מפירות הגינה שלהם.
שחר וטל הקימו דוכן כדי למכור לימונדה מפירות הגינה שלהם.  3. ללא כל צל של ספק או רשת
3. ללא כל צל של ספק או רשת



































.jpg)
 .
.











 1. החלטה גורלית
1. החלטה גורלית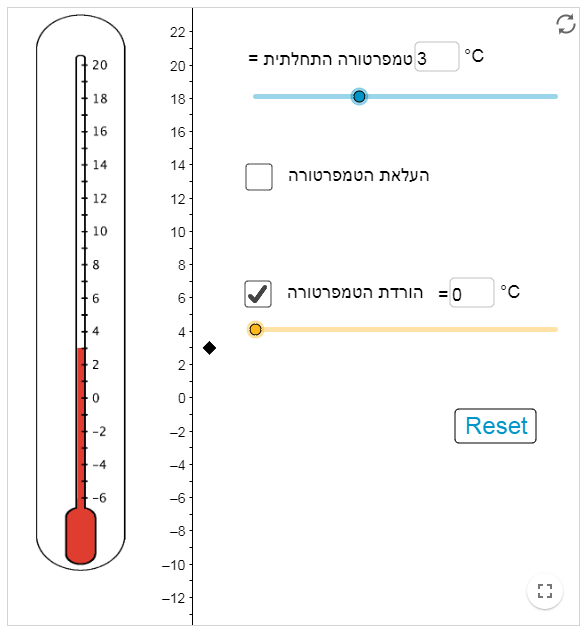 נושא: מספרים שליליים
נושא: מספרים שליליים



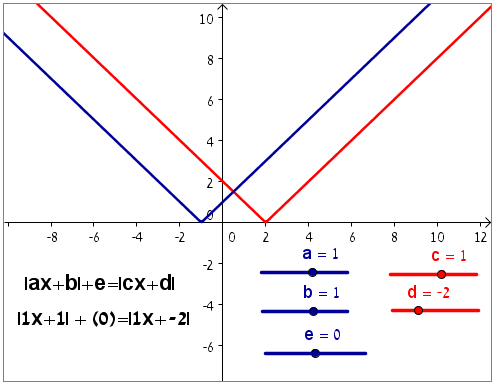























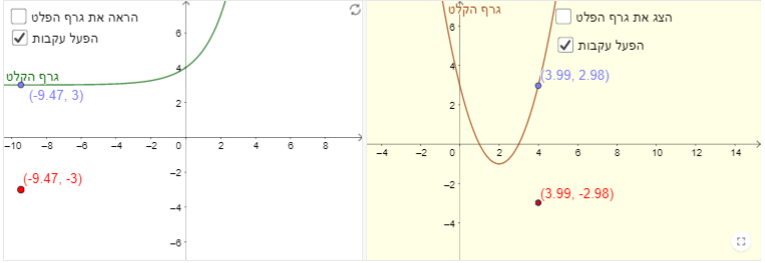

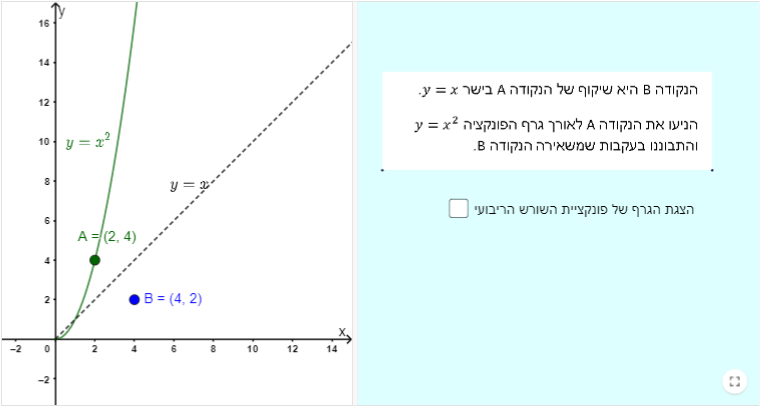
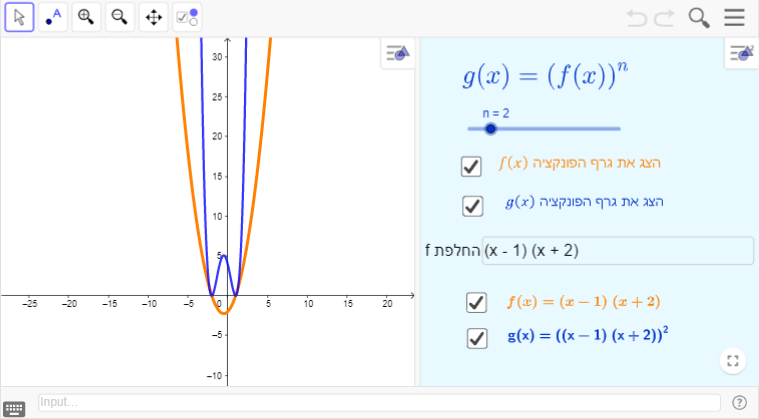






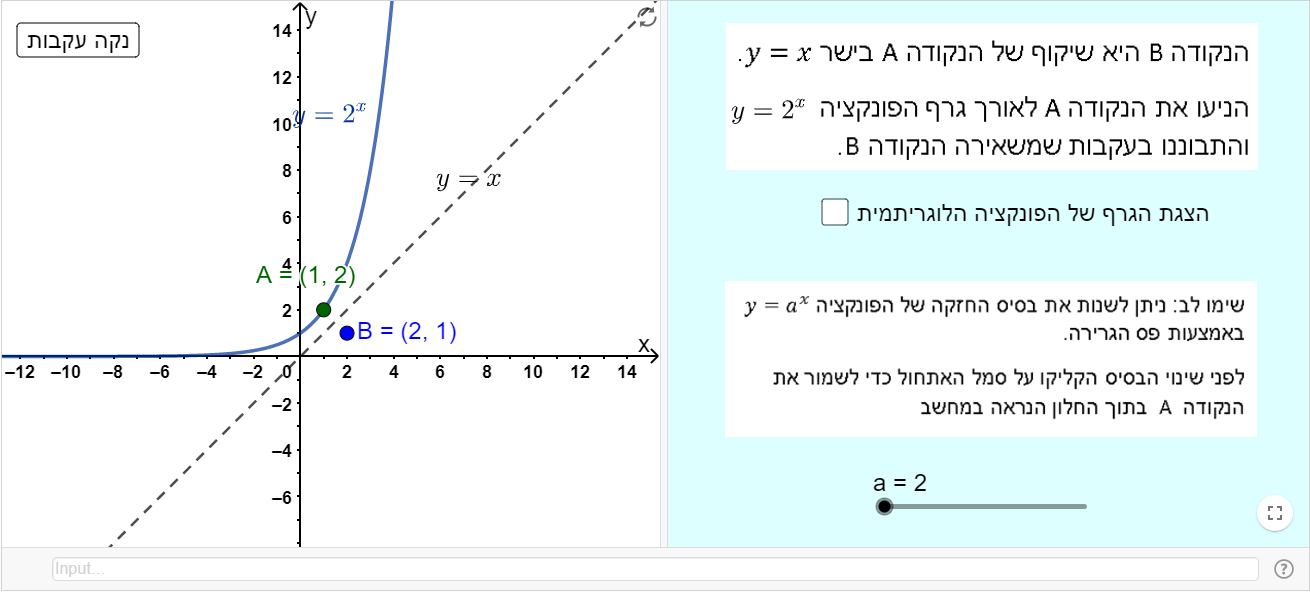
 נושא: הפונקציה - קדם אנליזה
נושא: הפונקציה - קדם אנליזה 












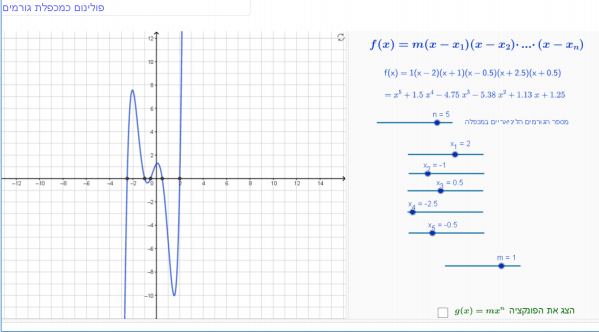
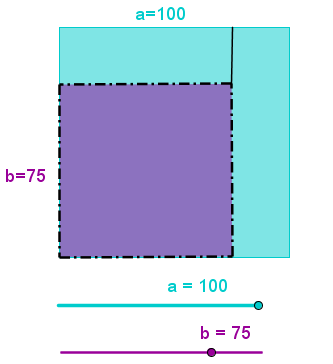
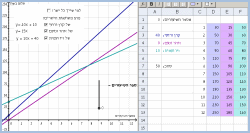
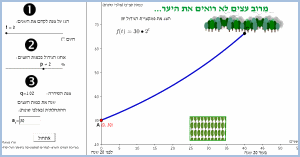
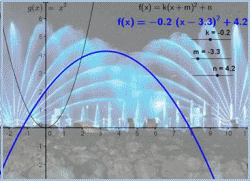
 נושא: פונקציה פולינומיאלית
נושא: פונקציה פולינומיאלית
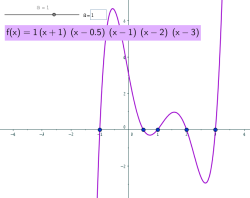
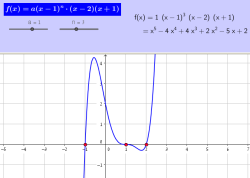



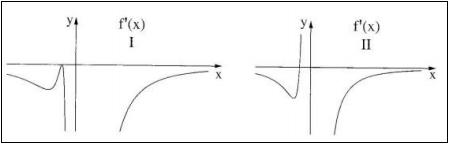















 תיאור:
תיאור: 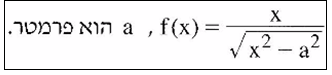 אל הפונקציה צעד אחר צעד
אל הפונקציה צעד אחר צעד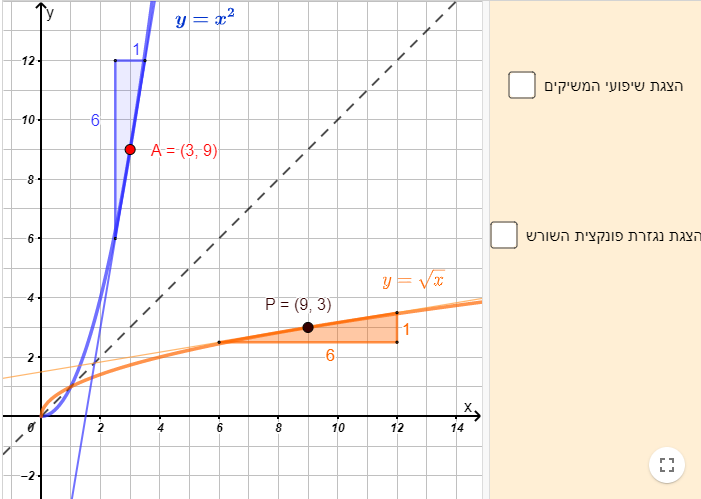
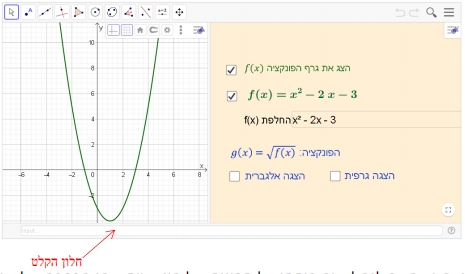



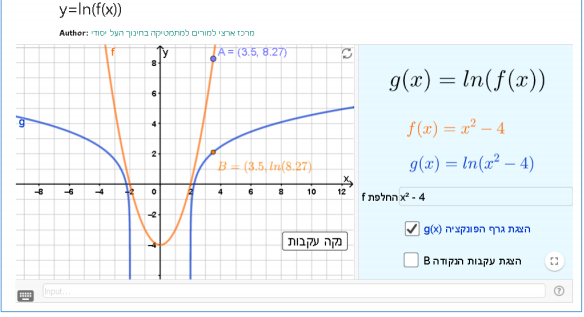 תיאור:
תיאור: 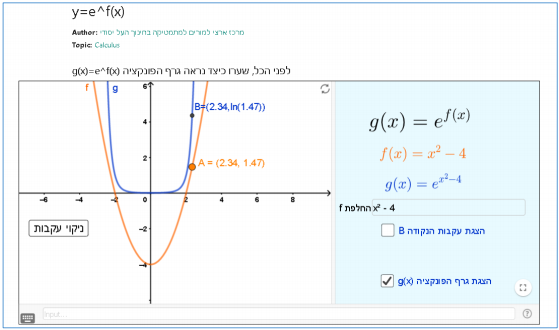 תיאור:
תיאור:  תיאור:
תיאור: 
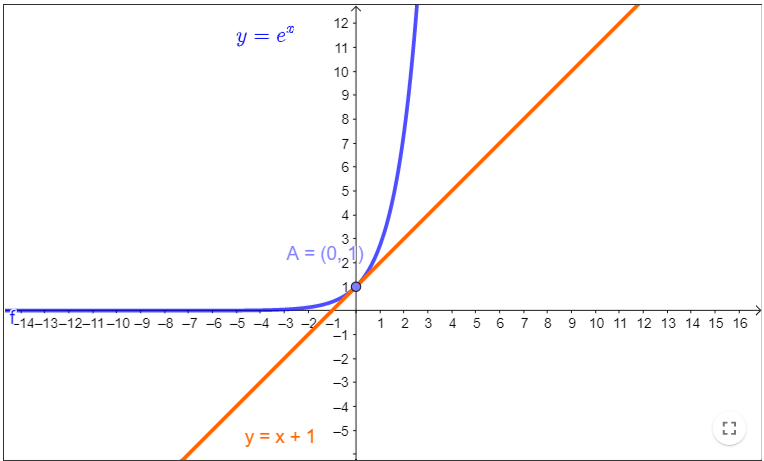





 נושא: שטחים, אינטגרלים.
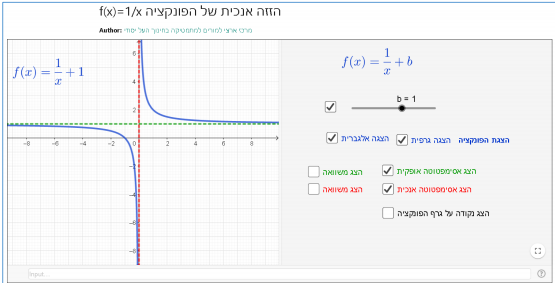
נושא: שטחים, אינטגרלים. נושא: אינטגרלים.
נושא: אינטגרלים.







 תיאור:
תיאור:  תיאור:
תיאור:  תיאור:
תיאור: 



