- עמוד הבית
- פונקציות וחדו"א
מאגר יישומים דינאמיים
פונקציות וחדו"א
נושא: הפונקציה - קדם אנליזה
כיתה: ט - י
תיאור: היישומון מופיע בפעילות: פונקציות מבעד למראה – שיקופים ביחס לצירים. היישומון מאפשר התבוננות בגרף של פונקציה המתקבל מגרף אחר באמצעות שיקוף בציר X. ההתבוננות יכולה להיות נקודתית (עקבות) או כללית. היישומון מצורף לפעילות שמפגישה את התלמידים, באמצעות שתי "מכונות", עם שתי טרנספורמציות פשוטות: האחת מבצעת שיקוף ביחס לציר ה-X. האחרת מבצעת שיקוף ביחס לציר ה- Y.
נושא: הפונקציה - קדם אנליזה
כיתה: ט - י
תיאור: היישומון מופיע בפעילות: פונקציות מבעד למראה – שיקופים ביחס לצירים. היישומון מאפשר התבוננות בגרף של פונקציה המתקבל מגרף אחר באמצעות שיקוף בציר Y. ההתבוננות יכולה להיות נקודתית (עקבות) או כללית. היישומון מצורף לפעילות שמפגישה את התלמידים, באמצעות שתי "מכונות", עם שתי טרנספורמציות פשוטות: האחת מבצעת שיקוף ביחס לציר ה-X. האחרת מבצעת שיקוף ביחס לציר ה- Y.
נושא: הפונקציה - קדם אנליזה
כיתה: י' או י"א
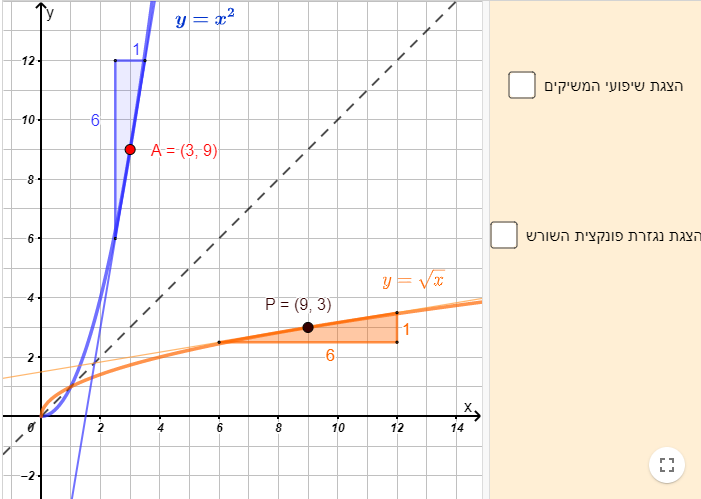
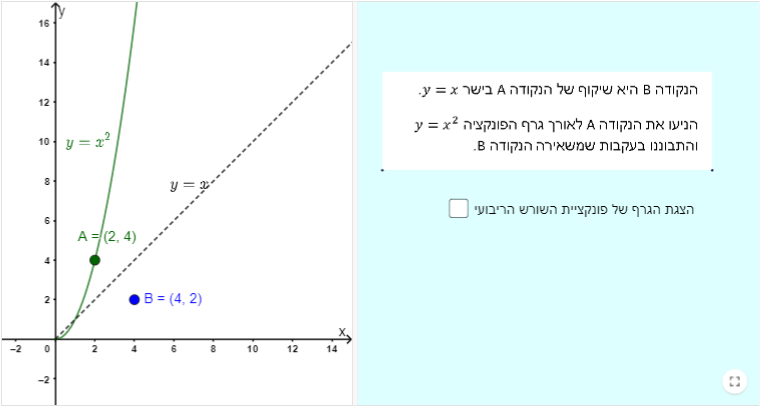
תיאור: היישומון מופיע בפעילות: אל הגרף של פונקציית השורש הריבועי, בה פונקציית השורש הריבועי והגרף שלה מוצגים באמצעות הקשר ביניהם לבין הענף החיובי של הפונקציה .y=x^2 ההיכרות עם הקשרים בין שתי הפונקציות האלה זורעת זרעים לקראת פעילות המשך, העוסקת בין הנגזרות של שתי הפונקציות האלה. ביישומון הדינמי גוררים נקודה על גרף הפונקציה y = x^2 ורואים את שיעורי הנקודה המתקבלת ממנה באמצעות שיקוף בישר y=x.
נושא: הפונקציה - קדם אנליזה
כיתה: י - י"א
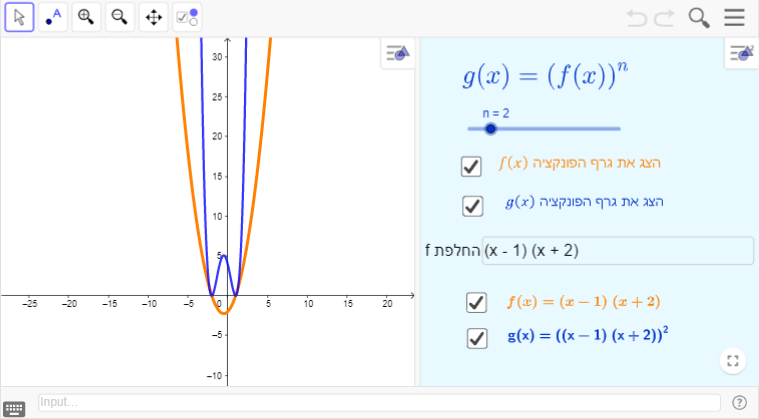
תיאור: יישומון זה מאפשר לנהל שיח כיתתי על תכונות של פונקציות שהן הרכבה של פונקציות חזקה עם מעריך טבעי (x^n) על פונקציה אחרת, כלומר פונקציות מהצורה: (f(x)^n), n מספר טבעי, ועל הקשר בין פונקציות אלה לבין הפונקציות הפנימיות שלהן. היישומון מאפשר, באמצעות סרגל גרירה לשנות את המעריך ולדון בתכונות שמאפיינות גרפים המתקבלים ממעריכים זוגיים לעומת תכונות של גרפים שמתקבלים ממעריכים אי-זוגיים.
נושא: הפונקציה - קדם אנליזה
כיתה: ט - י
תיאור: היישומון מאפשר לנהל שיח כיתתי שיעסוק בתכונות משפחת פונקציות זו, על שני חלקיה. ניתן גם לחבר עבור התלמידים משימות שבהן משולב היישומון. דוגמאות למשימות המבוססות על יישומון זה אפשר למצוא בפעילות "משפחת הפונקציות y=1/x^n מעריך טבעי".
נושא: הפונקציה - קדם אנליזה
כיתה: ט – י
תיאור: בעזרת היישומון ניתן לנהל שיח כיתתי שיעסוק בחקר הקשר בין תכונות הגרפים של פונקציות לבין הגרפים של הפונקציות המתקבלות מהכפלת ערכי הפונקציה בקבוע חיובי. לחילופין ניתן לחבר פעילויות לתלמידים שמנחות חקר כנ"ל ולשלב בהן את היישומון (ראו דוגמה בפעילות "מתיחה אנכית וכיווץ אנכי של גרף של פונקציה").
נושא: הפונקציה - קדם אנליזה
כיתה: י – י"ב
תיאור: יישומון זה מאפשר לנהל שיח כיתתי על תכונות של פונקציות שהן הרכבה של ערך מוחלט על פונקציה אחרת ועל הקשר בין פונקציות אלה לבין הפונקציות הפנימיות שלהן. ניתן גם לחבר עבור התלמידים משימות שבהן משולב היישומון.
נושא: הפונקציה - קדם אנליזה
כיתה: ט – י
תיאור: בעזרת יישומון זה ניתן לסרטט גרף של פונקציה נתונה וגרף של הפונקציה הופכית לה. אפשר לשנות את הפונקציה הנתונה לכל פונקציה אחרת (פולינומית, רציונאלית, שורש, טריגונומטרית ועוד) .בעזרת היישומון ניתן לנהל שיח כיתתי שיעסוק בחקר הקשר בין תכונות הגרפים של פונקציות לבין הגרפים של הפונקציות ההופכיות להן. לחילופין ניתן לחבר פעילויות לתלמידים שמנחות חקר כנ"ל ולשלב בהן את היישומון (ראו דוגמה בפעילות "פונקציה הופכית לפונקציה פולינומית“).
נושא: הפונקציה - קדם אנליזה
כיתה: ט – יא
תיאור: בעזרת יישומון זה ניתן לשקף גרף של פונקציה (f(x (פונקציית הקלט) ביחס לציר ה- x ולראות את הגרף המתקבל (g(x (פונקציית הפלט).
נושא: הפונקציה - קדם אנליזה
כיתה: ט – י
תיאור: בעזרת יישומון זה ניתן לשקף גרף של פונקציה (f(x (פונקציית הקלט) ביחס לציר ה- Y ולראות את הגרף המתקבל (g(x) (פונקציית הפלט).
נושא: הפונקציה - קדם אנליזה
כיתה: ט – י"א
תיאור: פעילות לכיתה בדסמוס לתרגול טרנפורציות של הזזות, מתיחות ושיקופים. ניתן להוסיף ולהעשיר את הפעילות.
מחבר: צוות דסמוס
נושא: הפונקציה.
כיתה: י, יא
תיאור: בעליה להר תבור היכן המטפס נמצא במקום התלול ביותר? דף עבודה ויישום דינאמי לחקירה של תכונת הקעירות כלפי מעלה וכלפי מטה. מעקב אחר שיפוע המשיק ומיקומו מעל ומתחת לגרף תרמוז לנו על נקודת הפיתול. כאן המקום לדון בקשר בין גרף הפונקציה לגרף הנגזרת הראשונה וכן גם הנגזרת השנייה.
נושא: הפונקציה.
כיתה: י-יב
תיאור: דף עבודה אינטראקטיבי ויישום דינאמי לחקירת השאלה כיצד משתנה גרף הפונקציה (הרציונאלית) כאשר מרכבים עליה את פונקצית הישר. האם וכיצד משתנות נקודות הקיצון? האם וכיצד משתנות האסימפטוטות. ניתן לבצע חקירה דומה על כל פונקציה אחרת.
מצורף גם דף עבודה שנכתב על ידי רבקה קלטוביץ על פי תרגילים מהספר (יואל גבע)
נושא: הפונקציה.
כיתה:
תיאור: יישום דינאמי בו ניתן להקליד פונקציה ולחקות את תהליך החקירה שלה. ניתן לצפות שלב אחר שלב באיפיוני הפונקציה כגון נקודות אפס, נקודות קיצון, אסימפטוטות מקבילות לצירים ורק אז ליצור את הגרף. ניתן גם להגדיר תחום סגור לפונקציה. היישום נוצר על ידי רותם ינקלוביץ במסגרת קורס גאוגברה תשע"ג.
נושא: הפונקציה
תיאור: יישום דינאמי לחקירת הקשר בין תכונת הזוגיות של הפונקציה לזוגיות הנגזרת. ניתן לבדוק את שיפועי המשיקים בנקודות סימטריות של הפונקציה.
נושא: הפונקציה
תיאור: דף עבודה אינטרקאטיבי ויישום דינאמי לחקירה של הקשר בין הנגזרות של פונקציות הפוכות. הנגזרת של פונקציה הפוכה שווה להופכי של נגזרת הפונקציה עצמה. הנחיה להוכחה אלגברית וכן להוכחה ויזואלית.
f(x ) = af(bx+c)+d
נושא: טרנספורמציות של פונקציות
כיתה: י'- יב'
תיאור: ניתן לחקור בעזרת היישום הדינאמי כיצד משפיע כל פרמטר בטרנספורמציה הלינארית על גרף הפונקציה. הכרות עם הזזות אנכיות ואופקיות וכן גם מתיחות אנכיות ואופקיות. ניתן לבצע את הטרנספורמציה על פונקציה ריבועית, פולינום ממעלה שלישית, טריגונומטרית או כל פונקציה אחרת.
נושא: הפונקציה.
כיתה: ט-י"ב
תיאור: מחשבון פונקציות המאפשר שינוי פרמטרים במשפחות של פונקציות (לינארית, ריבועית וערך מוחלט). מאפשר חקירת הזזות ומתיחות. וכמו כן מאפשר לבצע פעולות בין שתי הפונקציות: חיבור, חיסור, כפל וחילוק וכן הרכבה.
היישום הדינאמי נכתב על ידי פרופ' יהודה שוורץ, תורגם ונערך על ידי מרכז המורים
נושא: הפונקציה.
כיתה: ט'- י"ב
תיאור: בעזרת היישום הדינאמי ניתן לבדוק עבור אילו ערכי x הפונקציה עולה? מתי הפונקציה יורדת? ביישום הדינאמי ניתן לעקוב גם אחר הגרף, ערכי הנקודה שעל הגרף וטבלת ערכים. כמו כן ניתן לעקוב אחר משיקים בנקודות השונות שעל הפונקציה ואחר השתנות שיפוע המשיקים.
לעסוק בשאלה של הקשר בין עליה וירידה של הפונקציה ושיפועי המשיקים.
נושא: תכונות הפונקציה
כיתה: ט'- יב'
תיאור: בעזרת היישום הדינאמי ניתן לבדוק עבור אילו ערכי x ערכי הפונקציה חיוביים?
מתי הפונקציה שלילית?
נושא: הפונקציה.
כיתה: י-י"ב
תיאור: ישום דינאמי לחקירה של תכונות פונקציות הפוכות, התנאי לקיום פונקציה הפוכה והסימטריה לישר y=x.
נושא: הפונקציה.
כיתה: י-י"ב
תיאור: יישום דינאמי המאפשר לבדוק עבור פונקציות שונות האם הן זוגיות , אי זוגיות, או לא זה ולא זה.
פונקציה זוגית כאשר לכל נקודה יש על הפונקציה נקודה סימטרית ביחס לציר ה-y.
פונקציה אי זוגית כאשר לכל נקודה יש נקודה סימטרית ביחס לראשית.
מה הקשר בין שיעורי הנקודות הסימטריות?
נושא: הפונקציה.
כיתה: י-י"ב
תיאור: יישום דינאמי, פעילות ודף עבודה אינטראקטיבי לחקירת תכונות הפונקציה כגון עליה וירידה, קעירות כלפי מעלה וכלפי מטה לגרפים של פונקצית הנגזרת. וכן כיצד מושפעת הנגזרת מפעולות הזזה של הפונקציה? תורגם ונערך על פי האתר: GeogebraCalculus
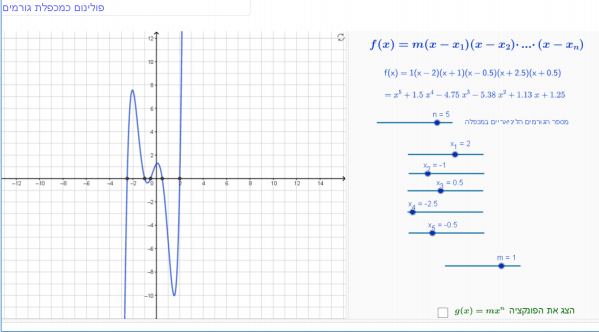
תיאור: יישומון זה מאפשר לנהל שיח כיתתי על התנהגות של פונקציות פולינום המוצגת כמכפלת גורמים ליניאריים. נציין, שכל פולינום ניתן להצגה כמכפלה של גורמים לינאריים ו/או גורמים ריבועיים אי-פריקים. יישומון זה מתייחס רק לפונקציות שניתנות להצגה כמכפלה של גורמים לינאריים בלבד.
נושא: פונקציה פולינומיאלית
תיאור: דף עבודה אינטראקטיבי ויישומון לחקירה של פונקציה ממעלה שלישית ותכונותיה המתקבלת על ידי מכפלה של ישר בפרבולה. פעילות זו יכולה להיות המשך לפעילות של פונקציה ריבועית כמכפלת פונקציות קוויות
נושא: פונקציה פולינומיאלית
כיתה: יא'- יב'
מבוסס על בחינת בגרות: שאלון 003, חורף תשע"א, שאלה 4.
תיאור: דף עבודה ויישום דינאמי המבוססים על שאלה מבחינת בגרות.
נושא: פונקציה פולינומיאלית
כיתה:
מבוסס על בחינת בגרות:
תיאור: דף עבודה אינטראקטיבי ויישום דינאמי לחקירת הגרפים של פולינומים המיוצגים כמכפלת גורמים לינאריים והשפעת ריבוי השורש על הגרף.
נושא: פונקציה פולינומיאלית
כיתה:
מבוסס על בחינת בגרות:
תיאור: דף עבודה אינטראקטיבי ויישום דינאמי בו ניתן לחקור כיצד משפיע ריבוי השורש (חזקת הגורם) על התנהגות גרף הפולינום.
נושא: פונקציה פולינומיאלית
כיתה: יא'-יב'
מבוסס על בחינת בגרות: שאלון 804, קיץ תש"ע, מועד ב', שאלה 9.
תיאור: דף עבודה ויישום דינאמי המבוססים על שאלה מבחינת בגרות.
נושא: פונקציה פולינומיאלית
כיתה: י'
תיאור: דף עבודה אינטראקטיבי ויישום דינאמי החוקרים את משפחת פונקציות החזקה בצורה המוזזת מהצורה f(x)=a(x-p)n+k . ראשית יש חלוקה לפונקצית חזקה זוגית ואי זוגית,. לאחר מכן חוקרים הזזות ומתיחות של פונקציות החזקה. פעילות זו היא הרחבה להכרות עם הפונקציה הריבועית בצורה הקודקודית.
נושא: פונקציה פולינומיאלית
כיתה: ז'- יב'
תיאור: יישום דינאמי לבניית מדרגה למדידת שיפוע דרך שתי נקודות שעל הפונקציה. ניתן לבנות מדרגות מספר, ומדרגות שונות על כל פונקציה.
נושא: פונקציה פולינומיאלית
כיתה: י - י"א
תיאור: יישומון זה מאפשר לנהל שיח כיתתי על תכונות של פונקציות שהן הרכבה של פונקציות חזקה עם מעריך טבעי (x^n) על פונקציה אחרת, כלומר פונקציות מהצורה: (f(x)^n), n מספר טבעי, ועל הקשר בין פונקציות אלה לבין הפונקציות הפנימיות שלהן. היישומון מאפשר, באמצעות סרגל גרירה לשנות את המעריך ולדון בתכונות שמאפיינות גרפים המתקבלים ממעריכים זוגיים לעומת תכונות של גרפים שמתקבלים ממעריכים אי-זוגיים.
נושא: אנליזה, הרכבת פונקציות, הקשר בין הגרף לנגזרת
כיתה: י' - יב'
שאלון: מבחן בגרות שאלון ראשון ברמת 5 יח"ל, 806- קיץ תשע"ו, מועד א'
תיאור:השאלה מתוך , מהווה בסיס לפעילות חקר והתנסות בעזרת יישומון בגאוגברה (להורדה).
בפעילות התלמיד מתבקש לחקור את הפונקציה באופן איכותני, כפונקציית חזקה מורכבת , ולהבחין בין חזקות זוגיות ואי זוגיות.
בפעילות גם הזמנה לתלמידים מתקדמים להמשיך ולבנות ולחקור.
נושא: תכונות הפונקציה- אנליזה
כיתה: מכיתה י והלאה
תיאור: יישומון זה מאפשר לקבוע אם פונקציה היא זוגית, אי-זוגית או שאינה זוגית ואינה אי-זוגית. היישומון נועד לשמש ככלי בשיח כיתתי העוסק במושגים: זוגיות של פונקציה ואי-זוגיות של פונקציה, ובמושגים נלווים כמו שיקוף בישר וסימטריה ביחס לנקודה. היישומון ניתן לשילוב גם בתוך פעילויות שמורים מחברים עבור כיתותיהם. דוגמה לשילוב היישומון בפעילות לתלמידים ניתן לראות בפעילויות פונקציה זוגית ואי- זוגית חלק א, חלק ב.
נושא: תכונות הפונקציה- אנליזה
כיתה: י – י"ב
תיאור: יישומון זה מאפשר לנהל שיח כיתתי על תכונות של פונקציות שהן הרכבה של ערך מוחלט על פונקציה אחרת ועל הקשר בין פונקציות אלה לבין הפונקציות הפנימיות שלהן. ניתן גם לחבר עבור התלמידים משימות שבהן משולב היישומון.
נושא: תכונות הפונקציה- אנליזה
כיתה: ט – י
תיאור: בעזרת יישומון זה ניתן לסרטט גרף של פונקציה נתונה וגרף של הפונקציה הופכית לה. אפשר לשנות את הפונקציה הנתונה לכל פונקציה אחרת (פולינומית, רציונאלית, שורש, טריגונומטרית ועוד) .בעזרת היישומון ניתן לנהל שיח כיתתי שיעסוק בחקר הקשר בין תכונות הגרפים של פונקציות לבין הגרפים של הפונקציות ההופכיות להן. לחילופין ניתן לחבר פעילויות לתלמידים שמנחות חקר כנ"ל ולשלב בהן את היישומון (ראו דוגמה בפעילות "פונקציה הופכית לפונקציה פולינומית“).
נושא: תכונות הפונקציה- אנליזה
כיתה: ט – י
תיאור: יישומון זה מציג גרפים של פונקציות מהמשפחה: y=x^n עם מעריך טבעי. הגרפים מוצגים בשני חלונות נפרדים, חלון לפונקציות עם מעריך זוגי וחלון לפונקציות עם מעריך אי-זוגי. היישומון מאפשר לנהל שיח כיתתי שיעסוק בתכונות משפחת פונקציות החזקה עם מעריך טבעי, על שני חלקיה. ניתן גם לחבר עבור התלמידים משימות שבהן משולב היישומון. דוגמאות למשימות המבוססות על יישומון זה אפשר למצוא בפעילות "פונקציית חזקה ממעלה זוגית וממעלה אי-זוגית".
נושא: תכונות הפונקציה- אנליזה
כיתה: י - י"ב
תיאור: בעליה להר תבור היכן המטפס נמצא במקום התלול ביותר?
דף עבודה ויישום דינאמי לחקירה של תכונת הקעירות כלפי מעלה וכלפי מטה.
מעקב אחר שיפוע המשיק ומיקומו מעל ומתחת לגרף תרמוז לנו על נקודת הפיתול.
כאן המקום לדון בקשר בין גרף הפונקציה לגרף הנגזרת הראשונה וכן גם הנגזרת השנייה.
נושא: תכונות הפונקציה- אנליזה
כיתה: י-י"ב
תיאור: יישום דינאמי בו ניתן להקליד פונקציה ולחקות את תהליך החקירה שלה.
ניתן לצפות שלב אחר שלב באיפיוני הפונקציה כגון נקודות אפס, נקודות קיצון, אסימפטוטות מקבילות לצירים ורק אז ליצור את הגרף.
ניתן גם להגדיר תחום סגור לפונקציה.
היישום נוצר על ידי רותם ינקלוביץ במסגרת קורס גאוגברה תשע"ג.
נושא: קשר בין גרף הפונקציה לגרף הנגזרת
כיתה: י"ב
תיאור: היישומון מופיע בפעילות: אל הנגזרת של הפונקציה y=lnx. היישומון מספק הסבר ויזואלי דינמי לביטוי האלגברי הפשוט של נגזרת הפונקציה y=lnx.
נושא: הפונקציה.
כיתה: י, יא
תיאור: בעליה להר תבור היכן המטפס נמצא במקום התלול ביותר? דף עבודה ויישום דינאמי לחקירה של תכונת הקעירות כלפי מעלה וכלפי מטה. מעקב אחר שיפוע המשיק ומיקומו מעל ומתחת לגרף תרמוז לנו על נקודת הפיתול. כאן המקום לדון בקשר בין גרף הפונקציה לגרף הנגזרת הראשונה וכן גם הנגזרת השנייה.
נושא: הקשר בין גרף הפונקציה לגרף הנגזרת שלה. 
כיתה: י'-יב' (3-4-5 יח"ל)
תיאור: ביישום הדינאמי ניתן לחקור את אופן השתנות הפונקציה מבחינת תחומי עליה וירידה, נקודות שיא ושפל (מקסימום ומינימום), נקודות פיתול והתנהגות המשיק לפונקציה בכל נקודה.
כל זאת תוך תנועת הדמות המצוירת. כמו כן ניתן לעקוב אחר השתנות השיפוע ותוך כדי לבנות את גרף הנגזרת.
ביישום מוצגת פונקצית הסינוס, אך ניתן לשנותה על ידי הקלדה של פונקציה חדשה
בחלון הקלט, למשל: f(x)=x3-3x.
נושא: הפונקציה.
כיתה: ט'- י"ב
תיאור: בעזרת היישום הדינאמי ניתן לבדוק עבור אילו ערכי x הפונקציה עולה? מתי הפונקציה יורדת? ביישום הדינאמי ניתן לעקוב גם אחר הגרף, ערכי הנקודה שעל הגרף וטבלת ערכים. כמו כן ניתן לעקוב אחר משיקים בנקודות השונות שעל הפונקציה ואחר השתנות שיפוע המשיקים.
לעסוק בשאלה של הקשר בין עליה וירידה של הפונקציה ושיפועי המשיקים.
נושא: הפונקציה.
כיתה: י-י"ב
תיאור: יישום דינאמי, פעילות ודף עבודה אינטראקטיבי לחקירת תכונות הפונקציה כגון עליה וירידה, קעירות כלפי מעלה וכלפי מטה לגרפים של פונקצית הנגזרת. וכן כיצד מושפעת הנגזרת מפעולות הזזה של הפונקציה? תורגם ונערך על פי האתר: GeogebraCalculus
נושא: הישר.
כיתה: ז- ח
תיאור: יישום דינאמי לחקירת עליה וירידה של הישר. ביישום סימולציה של שני שטחים מלבניים, האחד מתמלא בצבע באופן קבוע והשני מתרוקן מצבע באופן קבוע. ניתן לעקוב אחר השתנות גובה הצבע בטבלאות המספריות, ובנקודות המתארות את גובה הצבע כפונקציה של הזמן. תוך האנימציה ניתן לראות בבירור את תהליך העליה והירידה ולחקור את הקשר לייצוג האלגברי.
נושא: הישר.
כיתה: ח'- יב'
תיאור: דף עבודה אינטראקטיבי ויישום דינאמי לחקירת השפעת הפרמטרים על משוואת הישר y=ax+b. כמו כן יש אפשרות לשרטט מדרגות שונות על פי שתי נקודות על הישר.
נושא: הישר
כיתה: ז'- י'
תיאור: בעיה מילולית מתוך הפיצוח ערכים ומתמטיקה ובה חקירת פתרון שתי משוואות לינאריות, או חיתוך בין שני ישרים. הבעיה מלווה ביישום דינאמי לחקירה ולהמחשה ויזואלית של פתרון הבעיה. ביישום ניתן לחקור את הקשר בין הייצוג הטבלאי, הגרפי והאלגברי של הישרים ומציאת נקודת החיתוך ביניהם.
נושא: פונקציה ריבועית.
כיתה: ט
תיאור: הישומון מופיע בפעילות: למצוא את הפתרון הטוב ביותר – חלק א העוסקת בבעיות ערך קיצון, אותן ניתן לפתור באמצעות מציאת קודקוד של פרבולה. בישומון ניתן לעקוב אחר השינוי בשטח הרצפה בצמוד לשינוי בגרף הפונקציה המתארת אותו.
נושא: פונקציה ריבועית.
כיתה: ט
תיאור: היישומון מופיע בפעילות: למצוא את הפתרון הטוב ביותר – חלק א העוסקת בבעיות ערך קיצון, אותן ניתן לפתור באמצעות מציאת קודקוד של פרבולה. הישומון מתאים לבעיה העוסקת בשטח של גינה. ניתן לעקוב אחר שינוי בשטח הגינה בצמוד לשינוי בגרף הפונקציה המתארת אותו.
נושא: פונקציה ריבועית.
כיתה: ט
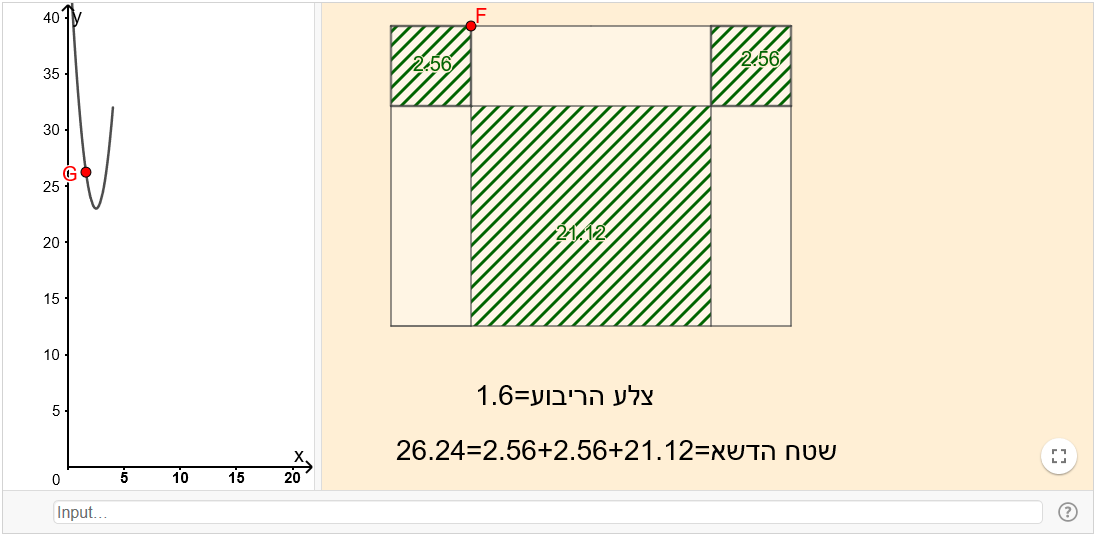
תיאור: היישומון מופיע בפעילות: למצוא את הפתרון הטוב ביתר – חלק ב. פעילות זו עוסקת במציאת מלבן בעל שטח גדול ביותר. היישומון מאפשר לעקוב אחר השתנות שטח הגינה כאשר משנים את צלעותיה.
נושא: פונקציה ריבועית.
כיתה: ט
תיאור: היישומון מופיע בפעילות: למצוא את הפתרון הטוב ביותר – חלק ג. פעילות זו עוסקת בבעיות ערך קיצון, אותן ניתן לפתור באמצעות מציאת קודקוד של פרבולה. היישומון מראה את השתנות אורך קטע בין שתי נקודות על שתי פרבולות, כאשר גוררים את אחת הנקודות.
נושא: פונקציה ריבועית.
כיתה: ט-י
תיאור: דף עבודה ויישום דינאמילחקירת גרף הפונקציה הריבועית המוצגת בצורה המוזזת (נקראת גם הצורה הקודקודית).
נושא: פונקציה ריבועית
תיאור:יישום דינאמי לתרגול הכרת הפונקציה הריבועית בצורה המוזזת או בצורה הקודקודית.
היישום נכתב על ידי מירטה לוין, ונערך על ידי מרכז המורים
נושא: פונקציה ריבועית
תיאור: יישום דינאמי לחקירת גרף הפונקציה הריבועית המוצגת בצורתו המוזזת. כיצד נמצא את ציר הסימטריה והקודקוד? אילו פרמטרים וכיצד משפיעים על מיקום הקודקוד? ניתן לבדוק ביישום נקודות סימטריות על הפרבולה בעזרת חיתוך עם ישר המקביל לציר x.
ניתן לשלב יחד עם דף העבודה והיישום לבעיה.
נלקח ממאגר 802.
נושא: פונקציה ריבועית
כיתה: ט-י
תיאור: יישום דינאמי לחקירת גרף הפונקציה הריבועית המוצגת בצורתו הסטנדרטית. כיצד נמצא את ציר הסימטריה והקודקוד? אילו פרמטרים וכיצד משפיעים על מיקום הקודקוד? ניתן לבדוק ביישום נקודות סימטריות על הפרבולה בעזרת חיתוך עם ישר המקביל לציר x.
ניתן לשלב יחד עם דף העבודה והיישום לבעיה.
נלקח ממאגר 802.
נושא: פונקציה ריבועית.
כיתה: ט-י
תיאור: יישום דינאמי לחקירת גרף הפונקציה הריבועית המוצגת בצורת המכפלה. כיצד נמצא את נקודות החיתוך עם ציר x? כיצד נמצא את ציר הסימטריה והקודקוד? ניתן לבדוק ביישום נקודות סימטריות על הפרבולה בעזרת חיתוך עם ישר המקביל לציר x.
ניתן לשלב יחד עם דף העבודה והיישום לבעיה.
נלקח ממאגר 802.
נושא: פונקציה ריבועית
כיתה: י-יא
תיאור: דף עבודה ויישום דינאמי לחקירת הקשר בין פונקציה ריבועית בצורה המוזזת וההופכית לה. בעזרת היישום התלמידים בונים את גרף הפונקציה הרציונאלית על פי תכונות הפונקציה הריבועית המוכרת להם. חוקרים את התכונות של פונקציה רציונאלית, תחומי ההגדרה אסימפטוטות, נקודות קיצון וכדומה. חקירה של משפחות ותת משפחות והשפעת הפרמטרים על הגרפים.
נושא: פונקציה ריבועית.
כיתה:
מבוסס על בחינת בגרות: המאגר החדש, שאלון 802-פונקציות, שאלה 5.
תיאור: דף עבודה ויישום דינאמי המבוססים על שאלה מבחינת בגרות.
נושא: פונקציה ריבועית.
כיתה:
מבוסס על בחינת בגרות: המאגר החדש, שאלון 802-פונקציות, שאלה 14.
תיאור: דף עבודה ויישום דינאמי המבוססים על שאלה מבחינת בגרות.
נושא: הפונקציה הריבועית
כיתה: ט'- יב'
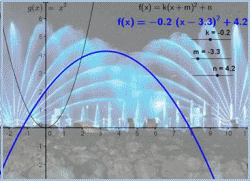
תיאור: ביישום הדינאמי ניתן לבצע טרנספורמציות של פרבולה בהצגה הקודקודית של פונקציה ריבועית.
שינוי הפרמטרים בתבנית f(x)=k(x+m)2+n.
הזזות ומתיחות של גרף הפרבולה והקשר להצגה האלגברית של הפונקציה הריבועית. בפעילות יש להתאים פונקציה ריבועית לתמונה נתונה של פרבולות (כמזרקה), על ידי שינוי הפרמטרים בהצגה הקודקודית.
תיאור: יישומון זה מאפשר לנהל שיח כיתתי על תכונות של פונקציות שהן הרכבה של שורש ריבועי על פונקציה אחרת ועל הקשר בין פונקציות אלה לבין הפונקציות הפנימיות שלהן. ניתן גם לחבר עבור התלמידים משימות שבהן משולב היישומון.
אל הפונקציה צעד אחר צעדנושא: אנליזה, חקירת פונקציות מנה עם שורש, אינטגרל
כיתה: יא'
שאלון: שאלון ראשון ב5 יח"ל- 806 - חרף תשעז- שאלה 7
תיאור: בפעילות נתבונן בפונקציה נתונה מתוך שאלת הבגרות. בפעילות שני חלקים:
בראשון הנחיה לחקור משפחה של פונקציות, פונקצית מנה עם שורש , באופן איכותני, ללא נגזרת.נסתכל על בניית פונקציה, צעד אחר צעד בעזרת פעולות על פונקציה כגון: הרכבה של פונקצית שורש, מציאת פונקציה הופכית , וכפל פונקציות. בפעילות התייחסות לתכונות של הפונקציה הנחקרת, וכן למקרים פרטיים במשפחה (a=0).
בחלק השני, התבוננות באינטגרלים והקשר שלהם לשטחים ולתכונות הפונקציה.
מומלץ להיעזר בחקירת הפונקציות בתוכנה גרפית כגון גאוגברה או desmos.
נושא: פונקציית השורש
כיתה: י' או י"א
תיאור: היישומון מופיע בפעילות: אל הגרף של פונקציית השורש הריבועי, בה פונקציית השורש הריבועי והגרף שלה מוצגים באמצעות הקשר ביניהם לבין הענף החיובי של הפונקציה .y=x^2 ההיכרות עם הקשרים בין שתי הפונקציות האלה זורעת זרעים לקראת פעילות המשך, העוסקת בין הנגזרות של שתי הפונקציות האלה. ביישומון הדינמי גוררים נקודה על גרף הפונקציה y = x^2 ורואים את שיעורי הנקודה המתקבלת ממנה באמצעות שיקוף בישר y=x.
נושא: פונקציית השורש
כיתה: י' או י"א
תיאור: היישומון מופיע בפעילות: אל הנגזרת של פונקציית השורש הריבועי. ביישומון מוצג הקשר בין שיפועי המשיקים של פונקציית השורש הריבועי לשיפועי המשיקים של הענף החיובי של הפונקציה y=x^2.
נושא: פונקציית השורש
כיתה: י - י"א
תיאור: יישומון זה מאפשר לנהל שיח כיתתי על תכונות של פונקציות שהן הרכבה של שורש ריבועי על פונקציה אחרת ועל הקשר בין פונקציות אלה לבין הפונקציות הפנימיות שלהן. ניתן גם לחבר עבור התלמידים משימות שבהן משולב היישומון. נשים לב שהתפריט להציג או להסתיר את הגרפים ואת התצוגה האלגברית, בהתאם למטרת השיעור.
נושא: פונקציית השורש.
כיתה: יא'-יב'
תיאור: דף עבודה ויישום דינאמי המבוססים על שאלה מבחינת בגרות.
מבוסס על בחינת בגרות:שאלון 804, קיץ תש"ע, מועד ב', שאלה 9.
נושא: פונקציית השורש 
כיתה: י-י"ב
תיאור: דף עבודה ויישום דינאמי לחקירה של הרכבת פונקצית השורש על פונקצית הישר ועל פונקציה ריבועית.
נושא: פונקציית השורש
כיתה: י-י"ב
תיאור: דף עבודה ויישום דינאמי לחקירה של פונקציות שונות עם שורש.
ביישום שתי פונקציות שורש של פונקציה לינארית.
נשאלת השאלה האם וכיצד משתנה תחום ההגדרה בפעולות סכום ומכפלת הפונקציות.
בדף העבודה משימות המאירות נקודות בעייתיות במציאת תחום ההגדרה.
נושא: פונקציית השורש
כיתה: י-י"ב
תיאור: דף עבודה (המכיל סרטוני הדגמה) ויישום דינאמי לחקירה של הרכבת פונקצית השורש על פונקציה לינארית, פונקציה ריבועית וערך מוחלט.
חקר סביב השאלה "האם ריבוע של שורש שווה לשורש של ריבוע".
דף העבודה מלווה בסרטוני הנחייה לחקר.
היישומון מתבסס על היישומון של פרופ' יהודה שוורץ מתוך האתר mathMINDShabits
נושא: פונקציית השורש 
כיתה: י-י"א
תיאור: יישום דינאמי
מבוסס על בחינת בגרות: שאלון 804, מועד ב' 2006, שאלה 7.
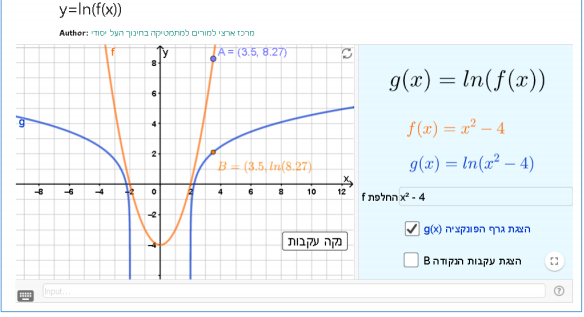תיאור: יישומון זה מאפשר לנהל שיח כיתתי על תכונות של פונקציות המתקבלות כאשר מרכיבים את הפונקציה y=lnx על פונקציה אחרת, כלומר על פונקציות מהצורה: (y=lnf(x
הדיון מעמיק בקשרים בין התכונות של פונקציה מורכבת לבין תכונות הפונקציות המרכיבות אותה.
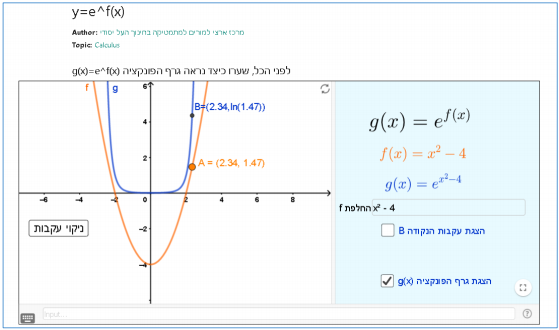תיאור: יישומון זה מאפשר לנהל שיח כיתתי על תכונות של פונקציות המתקבלות כאשר מרכיבים את הפונקציה y=e^x על פונקציה אחרת, כלומר על פונקציות מהצורה: (y=e^f(x
הדיון מעמיק בקשרים בין התכונות של פונקציה מורכבת לבין תכונות הפונקציות המרכיבות אותה.
תיאור: פעילות לכיתה בדסמוס לתרגול התכונות של פונקציות מעריכיות. ניתן להוסיף ולהעשיר את הפעילות.
הפעילות מתאימה לכיתות י"ב בנושא: פונקציות מעריכיות.
מחבר: צוות דסמוס
נושא: פונקציה מעריכית ולוגריתמית
כיתה:
מבוסס על בחינת בגרות: 2006, שאלון 007, מועד ב'.
תיאור: יישום דינאמי
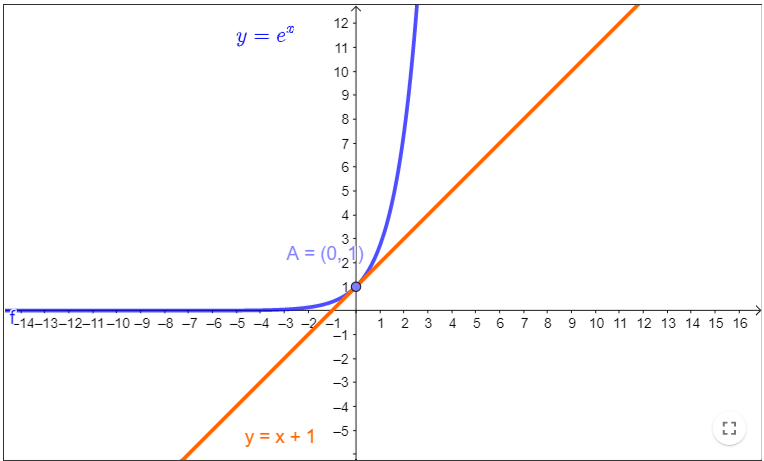נושא: פונקציה מעריכית ולוגריתמית
כיתה: י"ב
תיאור: היישומון מופיע בפעילות: אל הנגזרת של הפונקציה y=lnx. היישומון מספק הסבר ויזואלי דינמי לביטוי האלגברי הפשוט של נגזרת הפונקציה y=lnx.
נושא: אל נגזרת הפונקציה y=ln(x)
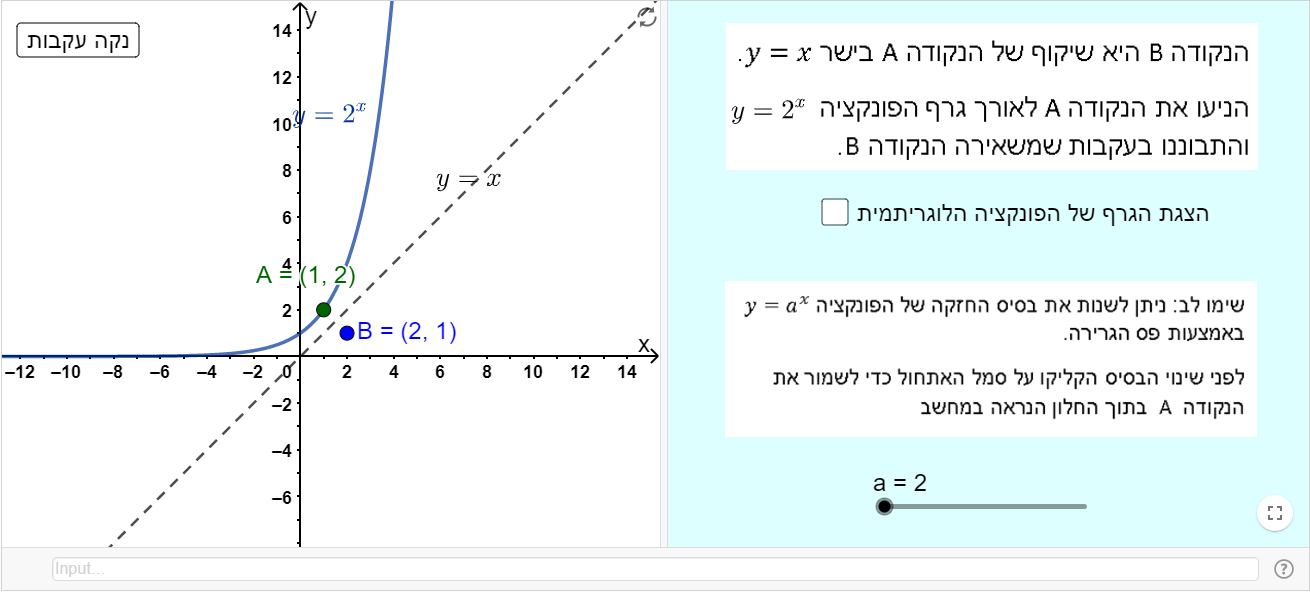
כיתה: י"ב
תיאור: היישומון מופיע בפעילות: אל הנגזרת של הפונקציה y=lnx. היישומון מספק הסבר ויזואלי דינמי לביטוי האלגברי הפשוט של נגזרת הפונקציה y=lnx.
נושא: פונקציה מעריכית ולוגריתמית
כיתה: י"ב
תיאור: היישומון מופיע בפעילות: אל הגרפים של הפונקציות הלוגריתמיות- חלק א+חלק ב. היישומון מאפשר לחקור את הקשרים בין הפונקציות הלוגריתמיות לבין הפונקציות המעריכיות המתאימות להן. בחלק א של הפעילות עוסקים בפונקציות y=logax a>1, ובחלק ב של הפעילות עוסקים בפונקציות y=logax, 0<a<1.
נושא: אורך קטע בין פונקציות לוגריתמיות.
כיתה: י"א- י"ב
תיאור: דף עבודה ויישום דינאמי המבוססים על שאלה מבחינת בגרות.
מבוסס על בחינת בגרות:שאלון 004, חורף תשס"ח, שאלה 5.
נושא: פונקציה מעריכית ולוגריתמית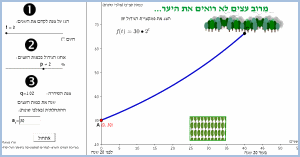
כיתה: י"א-י"ב
תיאור: דף עבודה ויישום דינאמי המבוססים על שאלה ממאגר 802 העוסקת בגדילה מעריכית של עצים ביער.
היישום מתאים כמובן גם ללומדים לשאלון 805 או 807.
ביישום ניתן לחקור כיצד משפיעים הפרמטרים השונים של פונקצית הגדילה על הגרף הן בייצוג הגרפי, הטבלאי והויזואלי.
מבוסס על בחינת בגרות: המאגר החדש, שאלון 802, שאלה 2.
נושא: פונקציה מעריכית ולוגריתמית
כיתה: י"א-י"ב
תיאור: דף עבודה ויישום דינאמי המבוססים על שאלה ממאגר 802 העוסקת בדעיכה מעריכית של חומר רדיואקטיבי.
היישום מתאים כמובן גם ללומדים לשאלון 805 או 807.
ביישום ניתן לחקור כיצד משפיעים הפרמטרים השונים של פונקצית הדעיכה על הגרף הן בייצוג הגרפי, הטבלאי והויזואלי.
כמו כן ניתן לעקוב אחר ערכים של הפונקציה. וכן להתרשם מקצב הדעיכה באנימציה של המיכל המתרוקן.
מבוסס על בחינת בגרות: המאגר החדש, שאלון 802, שאלה 8-9.
נושא: פונקציה מעריכית ולוגריתמית 
כיתה: י"א-י"ב
תיאור: דף עבודה ויישום דינאמי המבוססים על שאלה ממאגר 802.
הפעילות עוסקת בהשוואה בין עליה של המחירים של שתי דירות בגידול מעריכי.
ביישום ניתן להשוות ולקשר בין הייצוג הגרפי, הטבלאי והאלגברי.
ניתן לעקוב אחר ערכים וניתן גם לשנות את קבועי פונקצית הגידול.
מבוסס על בחינת בגרות: המאגר החדש, שאלון 802, שאלה 26.
נושא: הפונקציה מעריכית ולוגריתמית. 
כיתה: יב' (5 יח"ל)
תיאור: יישום דינאמי לחקירת הקשר בין הפונקציות ההפוכות המעריכית והלוגריתמית והסימטריה לישר y=x .
מתוך המצגת של ההרצאה "חדו"א של הפונקציות המעריכיות והלוגריתמיות" ובעיה מתוך הפיצוח "הפוך על הפוך".
נושא: הרכבה של פונקציות לוגריתמיות ((g(x)=ln(f(x
כיתה: יב' (4-5 יח"ל)
תיאור: דף עבודה אינטראקטיבי ויישום דינאמי לחקירה של הרכבת פונקציות מסוגים שונים על פונקציית ln .
ניתן לחקור בעזרת היישום הדינאמי כיצד משפיעה ההרכבה על תחומי העליה והירידה על נקודות הקיצון האסימפטוטות ועל גבולות הפונקציה באינסוף.
כמו כן נשאלת השאלה מתי נוצרת נקודת אי רציפות סינגולארית ("חור").
ניתן להכניס לחלון הקלט פונקציות שונות להרכבה.
הרחבה לפעילות בפיצוח עד קצה הגבול.
נושא: הרכבה של פונקציות על פונקציה מעריכית ((g(x)=e^(f(x
כיתה: יב' (4-5 יח"ל)
תיאור: דף עבודה אינטראקטיבי ויישום דינאמי לחקירה של הרכבת פונקציות מסוגים שונים על פונקצייה מעריכית.
ניתן לחקור בעזרת היישום הדינאמי כיצד משפיעה ההרכבה על תחומי העליה והירידה על נקודות הקיצון האסימפטוטות ועל גבולות הפונקציה באינסוף.
כמו כן נשאלת השאלה מתי נוצרת נקודת אי רציפות סינגולארית ("חור").
ניתן להכניס לחלון הקלט פונקציות שונות להרכבה.
הפעילות בהרחבה בפיצוח עד קצה הגבול
נושא: פונקציה מעריכית ולוגריתמית
כיתה: יא'- יב'
תיאור: דף עבודה ויישום דינאמי המבוססים על שאלה מבחינת בגרות.
מבוסס על בחינת בגרות:שאלון 004, חורף תשס"ט, שאלה 4.
נושא: שטחים, אינטגרלים.
כיתה: ז'-יב'
תיאור: הדגמה דינאמית, בעזרת יישום, של ההוכחה כי השטח באיור של שני העקומים החסומים בין מקבילים ואשר ה"רוחב" של כל אחד מהם זהה, שווה. ניתן לשנות את העקום על ידי גרירת הנקודות.
מתוך המאמר: ידע אינטואיטיבי וידע לוגי כמרכיבים של הפעילות המתמטית, אפרים פישביין, דינה תירוש ואביבה ברש, על"ה 22.
נושא: אינטגרלים.
כיתה: יא-יב.
תיאור: יישומון דינאמי בו ניתן להדגים סיבוב שטח בין גרף של פונקציה לבין ציר ה-x. מלווה במצגת בה סרטונים קצרים להדגמה.
נושא: אנליזה, אינטגרל
כיתה: יא' - יב'
שאלון: בעקבות שאלה 4-ג, בחינת הבגרות – 35807 – קיץ תשע"ו, מועד א.
תיאור: הפעילות עוסקת בקשר שבין פונקציה, אינטגרל מסויים, ופונקציה שמוגדרת באמצעותו – פונקציית ההצטברות שנקרא לה כאן פונקצית האינטגרל. הפעילות היא פעילות חקר מלווה ביישומון בגאוגברה.
נושא: אינטגרלים.
כיתה: י'-י"ב
תיאור: יישום דינאמי לחקירה של יחס השטחים של פונקצית חזקה.
גרף פונקצית החזקה מחלק ריבוע באורך יחידה לשני שטחים.
מצאו מהו יחס השטחים והאם הוא תלוי במעלת החזקה?
נושא: אינטגרלים.
כיתה: י-י"ב
תיאור: דף עבודה ויישום דינאמי המבוססים על שאלה מבחינת בגרות.
מבוסס על בחינת בגרות: שאלון 806, קיץ תשע"א, מועד ב', שאלה 9.
נושא: אינטגרלים.
כיתה: יא'-יב'
תיאור: דף עבודה ויישום דינאמי המבוססים על שאלה מבחינת בגרות.
מבוסס על בחינת בגרות:שאלון 004, חורף תש"ע, שאלה 4.
נושא: אינטגרלים.
כיתה: י, יא, יב
תיאור: יישום דינמי לחקירה והמחשה של חישוב השטח הכלוא מתחת לגרף הפונקציה בעזרת סכומי רימן.
ביישום ניתן לקבוע את גבולות השטח הכלוא וכן את מספר המלבנים המחלקים את השטח.
נושא: הגדרת הנגזרת
כיתה: י"ב
תיאור: היישומון מופיע בפעילות: אל הנגזרת של הפונקציה y=lnx. היישומון מספק הסבר ויזואלי דינמי לביטוי האלגברי הפשוט של נגזרת הפונקציה y=lnx.
נושא: הגדרת הנגזרת.
כיתה: י'- יב'
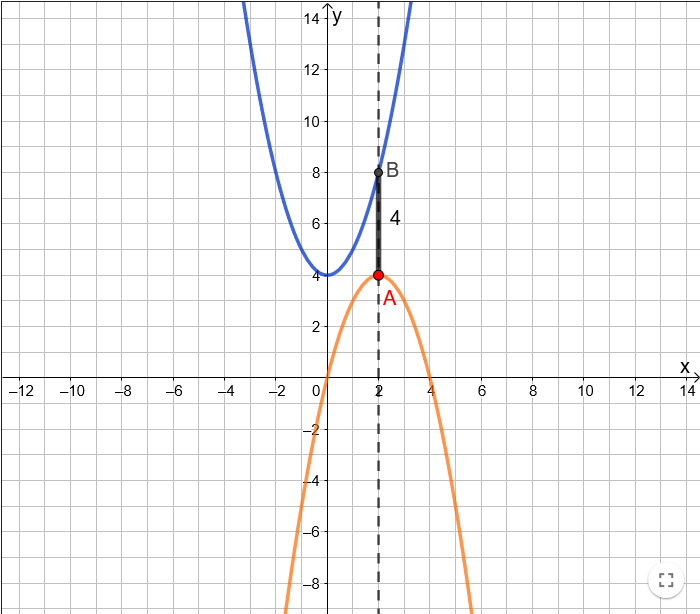
תיאור: יישום דינאמי להמחשת הגדרת הנגזרת כשיפוע המשיק שהוא גבול שיפוע החותכים.
ביישום מוצג המשיק לפונקציה y=x2 בנקודה A בה x=1 וישר חותך AB, בין שתי נקודות שעל הפונקציה.
ניתן להזיז את נקודה B, ולעקוב אחר שינוי שיפוע החותך ואופן חישוב שיפוע החותך.
ככל שהנקודה B מתקרבת לנקודה A, שיפוע החותך קרוב (מבחינה ויזואלית ומבחינה חישובית) לשיפוע המשיק.
ניתן לבצע תהליך זה גם עבור נקודות אחרות על הפונקציה. ניתן להקליד בחלון הקלט פונקציה אחרת. לדוגמא: f(x)=x3.
נושא: הגדרת הנגזרת. 
כיתה: י'-יא' (3-4-5 יח"ל)
תיאור: ביישום הדינאמי ניתן לחקור ולגלות את הכלל לנגזרת של פונקצית חזקה. בעזרת סרגל הגרירה משתנה החזקה של הפונקציה.
אפשר לעקוב בכל פונקצית חזקה מסויימת אחר השתנות שיפוע המשיקים בנקודות השונות (מומלץ לאסוף את הנתונים בטבלה) ומאידך אפשר לחקור את שינוי שיפוע המשיק עבור x מסוים לפונקציות חזקה שונות.
כמו כן, ניתן לעקוב אחר שרטוט השתנות המשיקים של כל פונקציה (הנגזרת).
נושא: פונקציות
כיתה: י-י"ב
תיאור: יישום דינאמי לחקירת הקשר בין תכונת הזוגיות של הפונקציה לזוגיות הנגזרת.
ניתן לבדוק את שיפועי המשיקים בנקודות סימטריות של הפונקציה ולשער מה הקשר בין הנגזרות של פונקציות הפוכות.
מומלץ להמשיך ולחקור בעזרת היישומון הנגזרת של פונקציה הפוכה.
נושא: פונקציות
כיתה: י-י"ב
תיאור: דף עבודה אינטרקאטיבי ויישום דינאמי לחקירה של הקשר בין הנגזרות של פונקציות הפוכות.
הנגזרת של פונקציה הפוכה שווה להופכי של נגזרת הפונקציה עצמה. הנחיה להוכחה אלגברית וכן להוכחה ויזואלית.
תיאור: היישומון מאפשר הכרות עם משפחת הפונקציות f(x)=(1/(x-a))+b. במיוחד מתאים להתייחס למשפחה זו כהזזה אופקית, אנכית או משולבת של גרף הפונקציה f(x)=1/x ולדון בהשפעה של ההזזה על האסימפטוטות של הפונקציה.
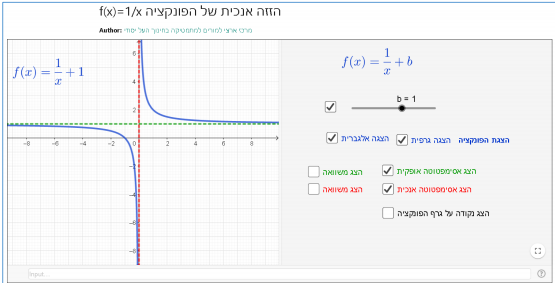תיאור: היישומון מאפשר הכרות עם משפחת הפונקציות f(x)=(1/x)+b. במיוחד מתאים להתייחס למשפחה זו כהזזה אנכית של גרף הפונקציה f(x)=1/x ולדון בהשפעה של ההזזה על האסימפטוטות של הפונקציה.
תיאור: יישומון מאפשר הכרות עם משפחת הפונקציות f(x)=1/(x-a) במיוחד מתאים להתייחס למשפחה זו כהזזה אופקית של גרף הפונקציה f(x)=1/x ולדון בהשפעה של ההזזה על האסימפטוטות של הפונקציה.
תיאור: יישומון זה מאפשר לנהל שיח כיתתי על הזזה אנכית של פונקציה, על הזזה אופקית של פונקציה ועל שילוב של שתי ההזזות. בפרט, היישומון מאפשר לדון בקשר בין הייצוג הגרפי לייצוג האלגברי של פונקציה המתקבלת מפונקציה אחרת באמצעות הזזה. ניתן גם לחבר עבור התלמידים משימות שבהן משולב היישומון.
נושא: פונקציה רציונאלית
כיתה: ט - י
תיאור: היישומון מאפשר לנהל שיח כיתתי שיעסוק בתכונות משפחת פונקציות זו, על שני חלקיה. ניתן גם לחבר עבור התלמידים משימות שבהן משולב היישומון. דוגמאות למשימות המבוססות על יישומון זה אפשר למצוא בפעילות "משפחת הפונקציות y=1/x^n מעריך טבעי".
נושא: פונקציה רציונאלית.
כיתה: י'- יב'
תיאור: דף עבודה אינטראקטיבי לחקירה של טרנספורמציות של היפרבולה. ניתן לחקור בעזרת היישום הדינאמי כיצד משפיעים הפרמטרים על גרף הפונקציה ועל מיקום האסימפטוטות האנכיות והאופקיות.
כמו כן ניתן לחקור את המעבר בין שני ייצוגים שקולים להיפרבולה.
הערה: ניתן להקדים את חקירת הנושא עוד לפני לימוד הנגזרות, כבר בכיתה י'.
נושא: פונקציה רציונאלית.
כיתה: יא'-יב'
תיאור: דף עבודה ויישום דינאמי המבוססים על שאלה מבחינת בגרות לחקירה של משפחת פונרציות רציונליות. חקירה כיצד משפיע הפרמטר על התנהגות גרף הפונקציה מבחינת נקודות חיתוך על הצירים, נקודות קיצון והאסימפטוטות האנכיות.
מבוסס על בחינת בגרות:שאלון 035004, קיץ תש"ע,מועד ב', שאלה 3.
נושא: פונקציה רציונאלית
כיתה: י-י"ב
תיאור: דף עבודה ויישום דינאמי. לחקירה ולתרגול של משפחת פונקציות מנה, כאשר במכנה החזקה משתנה. חקירה של הפרמטרים המשפיעים על הזזות ומתיחות של הגרף, על זוגיות הפונקציה, על האסימפטוטות ועוד.
דף העבודה מוביל להכללה ולתרגול הנושא. מתאים החל מרמת 3 יח"ל וכמובן גם לרמת 4-5 יח"ל.
נושא: פונקציה רציונאלית
כיתה: יא'- יב'
תיאור: דף עבודה ויישום דינאמי המבוססים על שאלה מבחינת בגרות.
מבוסס על בחינת בגרות: שאלון 004, מועד ב' תשס"ט, שאלה 3.
נושא: פונקציה רציונאלית
כיתה: י-יא
תיאור: דף עבודה ויישום דינאמי לחקירת הקשר בין פונקציה ריבועית בצורה המוזזת וההופכית לה.
בעזרת היישום התלמידים בונים את גרף הפונקציה הרציונאלית על פי תכונות הפונקציה הריבועית המוכרת להם.
חוקרים את התכונות של פונקציה רציונאלית, תחומי ההגדרה אסימפטוטות, נקודות קיצון וכדומה.
חקירה של משפחות ותת משפחות והשפעת הפרמטרים על הגרפים.
נושא: פונקציה רציונאלית.
כיתה: י-יב
תיאור: דף עבודה אינטראקטיבי ויישום דינאמי לחקירת השאלה כיצד משתנה גרף הפונקציה (הרציונאלית) כאשר מרכבים עליה את פונקצית הישר g(x)=ax+b.
האם וכיצד משתנות נקודות הקיצון?
האם וכיצד משתנות האסימפטוטות?
ניתן לבצע חקירה דומה על כל פונקציה אחרת.
מצורף גם דף עבודה שנכתב על ידי רבקה קלטוביץ על פי תרגילים מהספר (יואל גבע)
נושא: פונקציה רציונאלית 
כיתה: י-י"ב
תיאור: דף עבודה אינטראקטיבי ויישום דינאמי
מבוסס על בחינת בגרות: קיץ תשע"א, שאלון 805, שאלה 2.
נושא: פונקציה רציונלית 
כיתה: י-י"ב
תיאור: דף עבודה ויישום דינאמי לחקירה של התנהגות הפונקציה סביב נקודות אי הגדרה. ההבחנה בין נקודת אי רציפות סליקה ("חור") לבין אסימפטוטה. ובחינת השפעת ריבוי השורש על התנהגות הפונקציה סביב האסימפטוטה.
נושא: פונקציה רציונאלית
כיתה: י-י"ב
תיאור: דף עבודה ויישום דינאמי לחקירה של אי רציפות של פונקציה רציונאלית.
נושא: משפחות של פונקציית חזקה.
כיתה: י'
תיאור: דף עבודה ויישום דינאמי החוקרים את משפחת פונקציות החזקה בצורה המוזזת מהצורה f(x)=a(x-p)n+k .
ראשית יש חלוקה לפונקצית חזקה זוגית ואי זוגית.
לאחר מכן חוקרים הזזות ומתיחות של פונקציות החזקה.
פעילות זו היא הרחבה להכרות עם הפונקציה הריבועית בצורה הקודקודית.
נושא: פונקציה פולינומיאלית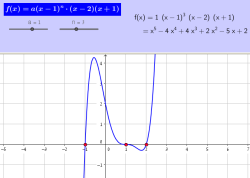
כיתה: י-י"א
תיאור: דף עבודה אינטראקטיבי ויישום דינאמי בו ניתן לחקור כיצד משפיע
ריבוי השורש (חזקת הגורם) על התנהגות גרף הפולינום.
מבוסס על בחינת בגרות:
נושא: פונקציה פולינומיאלית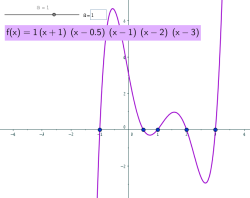
כיתה: י-י"א
תיאור: דף עבודה אינטראקטיבי ויישום דינאמי לחקירת הגרפים של פולינומים
המיוצגים כמכפלת גורמים לינאריים והשפעת ריבוי השורש על הגרף.
מבוסס על בחינת בגרות
נושא: קריאת גרפים
כיתה: ז - י
תיאור: דף עבודה אינטראקטיבי ויישום דינאמי לחקירת ההתאמה בין הפונקציה של שטחים בצורות שונות המתמלאים בצבע לפי הזמן, לבין הגרפים שלהם. ניתן לדון באופי השונה והדומה של קצב השתנות הפונקציות.
נושא: קריאת גרפים.
כיתה: ז'- ח'
תיאור: יישום דינאמי ובו מוצגים שני כלים מלבניים, האחד ריק ומתמלא בצבע עם הזמן, והשני מלא ומתרוקן עם הזמן. ניתן לעקוב בטבלת הערכים, בנקודות מתאימות על הגרף ולהתאים לכל אחד מהם את הפונקציה ואת הגרף המתאים. ביישום מומחשת מאד התופעה של עליה וירידה של פונקציה בייצוגיה השונים.
נושא: קריאת גרפים.
כיתה:
מבוסס על בחינת בגרות: המאגר החדש, שאלון 801, שאלה 21.
תיאור: דף עבודה ויישום דינאמי המבוססים על שאלה 21 בשאלון 801. ביישום מושם דגש על השיפועים השווים בגרף. יש אפשרות לשנות את השיפועים ולבדוק כיצד משתנה קצב גדילת השיער.
נושא: שאלות קיצון.
כיתה: י- יא'
תיאור: יישום הדינאמי לחקירת שאלת קיצון מתוך שאלון בגרות ראשון, חרף 2016.
נושא: שאלות קיצון.
כיתה: י- יא'
תיאור: יישום הדינאמי לחקירת שאלת קיצון מתוך שאלון בגרות ראשון, חרף 2017. היישום גם ממחיש את הקשר בין שטח המשולש ושטח האפור המשלים את הגזרה.
נושא: בעיות קיצון
כיתה: י' -יב'
שאלון: בחינת הבגרות במתמטיקה שאלון שני ב-3 יח"ל, 35803 , קיץ תשע"ו.:שאלה 6
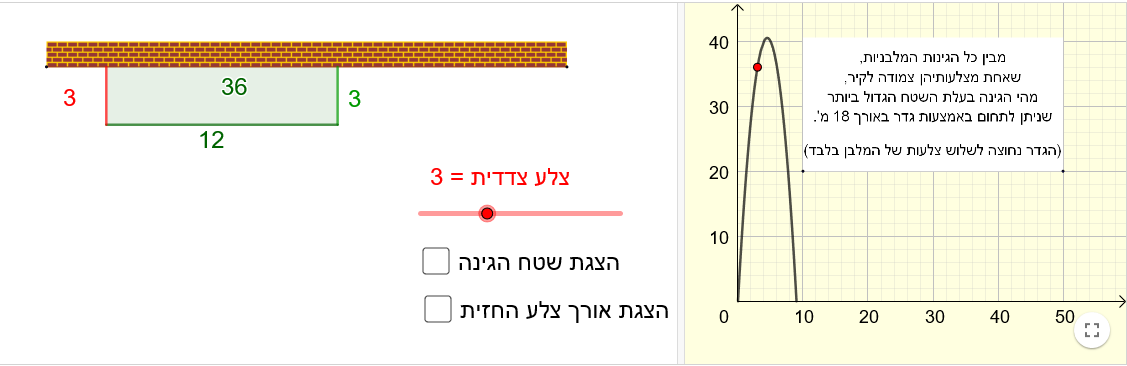
תיאור: המטרה העיקרית של הפעילות היא להדגיש שבבעיית ערך קיצון אנחנו מחפשים את הפתרון הטוב ביותר מבין כל הפתרונות האפשריים לבעיה.
הפעילות כוללת יישומון בגאוגברה, המאפשר לראות את מגוון האפשרויות לתכנן את הגינה, מציג את גרף הפונקציה המתאימה לארך צלע הריבוע את שטח הדשא, וממחיש את העובדה שהסרטוט הנתון בדף העבודה מתאר רק אפשרות אחת מתוך מגוון האפשרויות.
שני הסעיפים האחרונים הם הרחבה לשאלה. מתבוננים בפונקציה המתארת את סכום השטחים המיועדים לפרחים, ובודקים את הקשר בין שתי הפונקציות.
השאלה נבנתה עבור תלמידי 3 יח"ל אך בהחלט ניתן להתאימה לרמות גבוהות יותר בשלבים שונים של ההוראה.
נושא: בעיות קיצון.
כיתה:
תיאור: יישום דינאמי להמחשה ולחקר של בעיית קיצון. הבעיה מתאימה לשמש כשיעור פתיחה לנושא בעיות קיצון.
התלמידים מוזמנים לבנות תיבה על פי הדגם וליצור תיבה בעלת הנפח הגדול ביותר.
תיאור של שיעור פתיחה דומה הכי טוב שיש... - בעיות ערך קיצון מאת גילה רון.
היישום מתבסס על יישומון שכתב גיא הד.
נושא: בעיות קיצון.
כיתה: יא'- יב'
מבוסס על בחינת בגרות: שאלון 003, חורף תשס"ו, שאלה 5 - הכללה.
תיאור: יישום דינאמי - הכללה של השאלה על משולש הכלוא בפרבולה
נושא: בעיות קיצון.
תיאור: יישום דינאמי ודף עבודה אינטראקטיבי, לחקירה וסימולציה של בעית תנועה.
המרחק בין שני ישובים, A ו- B הוא 200 ק"מ. מכונית יצאה מהישוב A ליישוב B במהירות 60 קמ"ש. בו זמנית יצא רוכב אופנוע מהיישוב B ליישוב C במהירות 50 קמ"ש. כמה זמן אחרי שכלי הרכב יצאו לדרכם היה המרחק ביניהם מינימלי?
נושא: בעיות קיצון.
כיתה: ט
תיאור: הישומון מופיע בפעילות: למצוא את הפתרון הטוב ביותר – חלק א העוסקת בבעיות ערך קיצון, אותן ניתן לפתור באמצעות מציאת קודקוד של פרבולה. בישומון ניתן לעקוב אחר השינוי בשטח הרצפה בצמוד לשינוי בגרף הפונקציה המתארת אותו.
נושא: בעיות קיצון.
כיתה: ט
תיאור: היישומון מופיע בפעילות: למצוא את הפתרון הטוב ביותר – חלק א העוסקת בבעיות ערך קיצון, אותן ניתן לפתור באמצעות מציאת קודקוד של פרבולה. הישומון מתאים לבעיה העוסקת בשטח של גינה. ניתן לעקוב אחר שינוי בשטח הגינה בצמוד לשינוי בגרף הפונקציה המתארת אותו.
נושא: בעיות קיצון.
כיתה: ט
תיאור: היישומון מופיע בפעילות: למצוא את הפתרון הטוב ביתר – חלק ב. פעילות זו עוסקת במציאת מלבן בעל שטח גדול ביותר. היישומון מאפשר לעקוב אחר השתנות שטח הגינה כאשר משנים את צלעותיה.
נושא: בעיות קיצון.
כיתה: י"א- י"ב
תיאור: דף עבודה ויישום דינאמי המבוססים על שאלה מבחינת בגרות.
מבוסס על בחינת בגרות:שאלון 004, חורף תשס"ח, שאלה 5.
נושא: בעיות קיצון.
כיתה: י'-יא'
תיאור: ביישום הדינאמי מוצגת בעיה בה יש לחקור מהו הנפח (או שטח הפנים) המקסימלי של גליל החסום בחרוט נתון.
אפשר לשנות את רדיוס הגליל ולצפות באופן ויזואלי אחר השתנות הגליל עצמו ואחר השתנות ערכי הנפח שלו.
ניתן לשנות גם את מימדי החרוט.
נושא: בעיות קיצון.
כיתה: יא'-יב'
תיאור: דף עבודה ויישום דינאמי המבוססים על שאלה מבחינת בגרות.
מבוסס על בחינת בגרות: שאלון 035004, חורף תש"ע , שאלה 5.
נושא: בעיות קיצון.
כיתה: יא'- יב'
תיאור: דף עבודה ויישום דינאמי המבוססים על שאלה מבחינת בגרות.
מבוסס על בחינת בגרות:שאלון 006, מועד ב' תשס"ט, שאלה 5.
נושא: בעיות קיצון.
כיתה: יא'- יב'
תיאור: דף עבודה ויישום דינאמי המבוססים על שאלה מבחינת בגרות.
מבוסס על בחינת בגרות:שאלון 003, חורף תש"ע, שאלה 5.
נושא: בעיות קיצון. 
כיתה: י'-י"ב
תיאור: דף עבודה ויישום דינאמי לביצוע משימה בה שילוב של פונקצית הישר ופונקציה ריבועית.
מתוך משימות אוריינות לכיתה ט בנושא פונקציות
נושא: בעיות קיצון.
כיתה: י'- יב'
תיאור: דף עבודה ויישום דינאמי המבוססים על שאלה מבחינת בגרות.
מבוסס על בחינת בגרות:שאלון 003, קיץ תשס"ח, שאלה 5.
נושא: בעיות קיצון.
כיתה: יא'- יב'
תיאור: דף עבודה ויישום דינאמי המבוססים על שאלה מבחינת בגרות.
מבוסס על בחינת בגרות:שאלון 004, קיץ תשס"ט, מועד ב', שאלה 5.
נושא: בעיות קיצון.
כיתה: יא'- יב'
תיאור: דף עבודה ויישום דינאמי חדש המבוססים על שאלה מבחינת בגרות.
מבוסס על בחינת בגרות:שאלון 004, חורף תשע"א, שאלה 5.
נושא: בעיות קיצון.
כיתה: יא'- יב'
תיאור: דף עבודה ויישום דינאמי המבוססים על שאלה מבחינת בגרות.
מבוסס על בחינת בגרות:שאלון 003, קיץ תשס"ט, שאלה 5.
נושא: בעיות קיצון. 
כיתה: ט, י, יא
תיאור: יישום דינאמי לחקירת השאלה - מבין כל המלבנים בעלי היקף נתון ,
מהו המלבן בעל שטח מקסימלי?
נושא: בעיות קיצון.
כיתה: יא'- יב'
תיאור: דף עבודה ויישום דינאמי המבוססים על שאלה מבחינת בגרות.
מבוסס על בחינת בגרות:שאלון 004, קיץ תשס"ט, שאלה 5.
נושא: בעיות קיצון.
כיתה: יא'- יב'
תיאור: דף עבודה ויישום דינאמי המבוססים על שאלה מבחינת בגרות.
מבוסס על בחינת בגרות:שאלון 003, חורף תשס"ו, שאלה 5.
נושא: בעיות קיצון
כיתה: י"ב
תיאור: דף עבודה ויישום דינאמיהמבוססים על שאלה מבחינת בגרות.
מבוסס על בחינת בגרות: שאלון 807, קיץ תשע"ב, שאלה 4.
נושא: שטח הכלוא בפרבולה.
כיתה: י"א-י"ב
מבוסס על בחינת בגרות: שאלון 806, קיץ תשע"א, מועד ב', שאלה 9.
תיאור: דף עבודה ויישום דינאמי המבוססים על שאלה מבחינת בגרות.
נושא: מבעית קיצון בהנדסת המישור
כיתה: י-י"ב
תיאור: דף עבודה אינטרקטיבי ויישום דינאמי המבוססים על שאלה מבחינת בגרות.
נושא: בעיות קיצון. 
כיתה: י-י"ב
מבוסס על בחינת בגרות: שאלון 804 חרף תשע"ב
תיאור: מתבסס על בחינת בגרות, שאלון 804 חרף תשע"ב. דף עבודה ויישום דינאמי לחקירת בעית קיצון במשולש ישר זווית. בדף העבודה הנחיות לחקירה ולפתרון בדרכים שונות.
שימוש במשפט התיכון ליתר שווה למחציתו.
דף העבודה והיישום נוצרו על ידי עמרי נווה ובעריכת מרכז המורים.
נושא: בעיות קיצון 
תיאור: דף עבודה אינטראקטיבי ויישום דינאמי
להמחשה של בעית קיצון. בבעיה זו יש להתחשב במציאת המקסימום גם בתחום ההצבה של הפונקציה.
נושא: מספרים מרוכבים
תיאור: יישום דינאמי לחקירה והמחשה של מקומות גיאומטריים של מספרים מרוכבים במישור גאוס.
נושא: מספרים מרוכבים
כיתה:
תיאור: מתוך הפיצוח "לדמיין את המספרים המדומים" נמצא שורשים מדומים של משוואה ריבועית. חשבתם פעם האם ניתן לראות את השורשים המרוכבים של משוואה ריבועית בעזרת גרף הפרבולה? השורשים הממשיים של פונקציה ריבועית הם נקודות האפס של הפרבולה, אך היכן מסתתרים השורשים המרוכבים. נתבונן בפונקציות ריבועיות בהצגה הקודקודית (הצורה המוזזת), בעזרת יישום דינאמי בגאוגברה, ונגלה שיטה פשוטה לאתר את השורשים של הפרבולה במישור המרוכב.
נושא:שורשי היחידה של מספר מרוכב
כיתה:
תיאור: יישום דינאמי בו ניתן לראות באופן ויזואלי את שורשי היחידה ואת המצולע המשוכלל שהם יוצרים. כמו כן ניתן להציג את החזקות של שורשי היחידה.
תיאור: בעזרת יישומון זה ניתן להציג במערכת צירים אחת גרף של פונקציה f(x) וגרף של פונקציה g(x) המתקבלת ממנה על ידי הכפלתה בקבוע חיובי, כלומר g(x)=af(x). את ערכו של a אפשר לשנות באמצעות פס הגרירה. אפשר להחליף פונקציות ולראות את הייצוגים האלגבריים והגרפיים של הפונקציה המקורית ושל זו המתקבלת מהכפלתה בקבוע חיובי (a>0) בהתאם לערך של a תהיה זו מתיחה אנכית (a>1) או כיווץ אנכי (0<a<1). יש אפשרות להסתיר את הפונקציה המתקבלת מהמתיחה או מהכיווץ ולבקש מהתלמידים לשער כיצד ייראה הגרף שלה ואח"כ לבדוק בעזרת היישומון. אפשר לשנות את הפונקציה הנתונה לכל פונקציה אחרת (פולינומית, רציונאלית, שורש, טריגונומטרית ועוד). בעזרת היישומון ניתן לנהל שיח כיתתי שיעסוק בחקר הקשר בין תכונות הגרפים של פונקציות לבין הגרפים של הפונקציות המתקבלות מהכפלת ערכי הפונקציה בקבוע חיובי. לחילופין ניתן לחבר פעילויות לתלמידים שמנחות חקר כנ"ל ולשלב בהן את היישומון (ראו דוגמה בפעילות "מתיחה אנכית וכיווץ אנכי של גרף של פונקציה").
תיאור: בעזרת יישומון זה ניתן לסרטט גרף של פונקציה נתונה וגרף של הפונקציה הופכית לה. אפשר לשנות את הפונקציה הנתונה לכל פונקציה אחרת (פולינומית, רציונאלית, שורש, טריגונומטרית ועוד). בעזרת היישומון ניתן לנהל שיח כיתתי שיעסוק בחקר הקשר בין תכונות הגרפים של פונקציות לבין הגרפים של הפונקציות ההופכיות להן. לחילופין ניתן לחבר פעילויות לתלמידים שמנחות חקר כנ"ל ולשלב בהן את היישומון (ראו דוגמה בפעילות "פונקציה הופכית לפונקציה פולינומית").
נושא: פעולות על פונקציות
כיתה: ט - י
תיאור: היישומון מופיע בפעילות: פונקציות מבעד למראה – שיקופים ביחס לצירים. היישומון מאפשר התבוננות בגרף של פונקציה המתקבל מגרף אחר באמצעות שיקוף בציר x. ההתבוננות יכולה להיות נקודתית (עקבות) או כללית. היישומון מצורף לפעילות שמפגישה את התלמידים, באמצעות שתי "מכונות", עם שתי טרנספורמציות פשוטות: האחת מבצעת שיקוף ביחס לציר ה-X. האחרת מבצעת שיקוף ביחס לציר ה- Y.
נושא: פעולות על פונקציות
כיתה: ט - י
תיאור: היישומון מופיע בפעילות: פונקציות מבעד למראה – שיקופים ביחס לצירים. היישומון מאפשר התבוננות בגרף של פונקציה המתקבל מגרף אחר באמצעות שיקוף בציר Y. ההתבוננות יכולה להיות נקודתית (עקבות) או כללית. היישומון מצורף לפעילות שמפגישה את התלמידים, באמצעות שתי "מכונות", עם שתי טרנספורמציות פשוטות: האחת מבצעת שיקוף ביחס לציר ה-X. האחרת מבצעת שיקוף ביחס לציר ה- Y.
נושא: פעולות על פונקציות
כיתה: י - י"א
תיאור: יישומון זה מאפשר לנהל שיח כיתתי על תכונות של פונקציות שהן הרכבה של פונקציות חזקה עם מעריך טבעי (x^n) על פונקציה אחרת, כלומר פונקציות מהצורה: (f(x)^n), n מספר טבעי, ועל הקשר בין פונקציות אלה לבין הפונקציות הפנימיות שלהן. היישומון מאפשר, באמצעות סרגל גרירה לשנות את המעריך ולדון בתכונות שמאפיינות גרפים המתקבלים ממעריכים זוגיים לעומת תכונות של גרפים שמתקבלים ממעריכים אי-זוגיים.
נושא: פעולות על פונקציות
כיתה: ט – י
תיאור: בעזרת היישומון ניתן לנהל שיח כיתתי שיעסוק בחקר הקשר בין תכונות הגרפים של פונקציות לבין הגרפים של הפונקציות המתקבלות מהכפלת ערכי הפונקציה בקבוע חיובי. לחילופין ניתן לחבר פעילויות לתלמידים שמנחות חקר כנ"ל ולשלב בהן את היישומון (ראו דוגמה בפעילות "מתיחה אנכית וכיווץ אנכי של גרף של פונקציה").
נושא: פעולות על פונקציות
כיתה: י – י"ב
תיאור: יישומון זה מאפשר לנהל שיח כיתתי על תכונות של פונקציות שהן הרכבה של ערך מוחלט על פונקציה אחרת ועל הקשר בין פונקציות אלה לבין הפונקציות הפנימיות שלהן. ניתן גם לחבר עבור התלמידים משימות שבהן משולב היישומון.
נושא: פעולות על פונקציות
כיתה: ט – י
תיאור: בעזרת יישומון זה ניתן לסרטט גרף של פונקציה נתונה וגרף של הפונקציה הופכית לה. אפשר לשנות את הפונקציה הנתונה לכל פונקציה אחרת (פולינומית, רציונאלית, שורש, טריגונומטרית ועוד) .בעזרת היישומון ניתן לנהל שיח כיתתי שיעסוק בחקר הקשר בין תכונות הגרפים של פונקציות לבין הגרפים של הפונקציות ההופכיות להן. לחילופין ניתן לחבר פעילויות לתלמידים שמנחות חקר כנ"ל ולשלב בהן את היישומון (ראו דוגמה בפעילות "פונקציה הופכית לפונקציה פולינומית“).
נושא: פעולות על פונקציות
כיתה: ט – יא
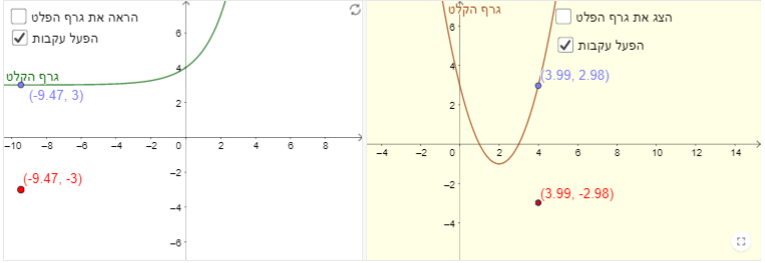
תיאור: בעזרת יישומון זה ניתן לשקף גרף של פונקציה f(x) (פונקציית הקלט) ביחס לציר ה- x ולראות את הגרף המתקבל g(x) )פונקציית הפלט(.
נושא: פעולות על פונקציות
כיתה: ט – י
תיאור: בעזרת יישומון זה ניתן לשקף גרף של פונקציה f(x) (פונקציית הקלט) ביחס לציר ה- Y ולראות את הגרף המתקבל g(x) )פונקציית הפלט(.
נושא: פעולות על פונקציות
כיתה: י - י"א
תיאור: יישומון זה מאפשר לנהל שיח כיתתי על תכונות של פונקציות שהן הרכבה של שורש ריבועי על פונקציה אחרת ועל הקשר בין פונקציות אלה לבין הפונקציות הפנימיות שלהן. ניתן גם לחבר עבור התלמידים משימות שבהן משולב היישומון. נשים לב שהתפריט להציג או להסתיר את הגרפים ואת התצוגה האלגברית, בהתאם למטרת השיעור.
