- עמוד הבית
- פונקציות וחדו"א
- תכונות הפונקציה (אנליזה)
מאגר יישומים דינאמיים
תכונות הפונקציה -אנליזה
נושא: תכונות הפונקציה- אנליזה
כיתה: ט – י
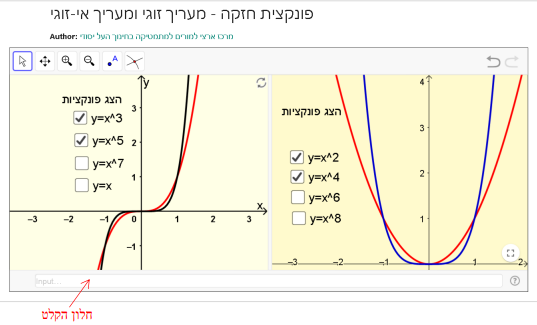
תיאור: יישומון זה מציג גרפים של פונקציות מהמשפחה: y=x^n עם מעריך טבעי. הגרפים מוצגים בשני חלונות נפרדים, חלון לפונקציות עם מעריך זוגי וחלון לפונקציות עם מעריך אי-זוגי. היישומון מאפשר לנהל שיח כיתתי שיעסוק בתכונות משפחת פונקציות החזקה עם מעריך טבעי, על שני חלקיה. ניתן גם לחבר עבור התלמידים משימות שבהן משולב היישומון. דוגמאות למשימות המבוססות על יישומון זה אפשר למצוא בפעילות "פונקציית חזקה ממעלה זוגית וממעלה אי-זוגית".
נושא: תכונות הפונקציה- אנליזה
כיתה: ט – י
תיאור: בעזרת יישומון זה ניתן לסרטט גרף של פונקציה נתונה וגרף של הפונקציה הופכית לה. אפשר לשנות את הפונקציה הנתונה לכל פונקציה אחרת (פולינומית, רציונאלית, שורש, טריגונומטרית ועוד) .בעזרת היישומון ניתן לנהל שיח כיתתי שיעסוק בחקר הקשר בין תכונות הגרפים של פונקציות לבין הגרפים של הפונקציות ההופכיות להן. לחילופין ניתן לחבר פעילויות לתלמידים שמנחות חקר כנ"ל ולשלב בהן את היישומון (ראו דוגמה בפעילות "פונקציה הופכית לפונקציה פולינומית“).
נושא: תכונות הפונקציה- אנליזה
כיתה: י – י"ב
תיאור: יישומון זה מאפשר לנהל שיח כיתתי על תכונות של פונקציות שהן הרכבה של ערך מוחלט על פונקציה אחרת ועל הקשר בין פונקציות אלה לבין הפונקציות הפנימיות שלהן. ניתן גם לחבר עבור התלמידים משימות שבהן משולב היישומון.
נושא: אנליזה, הרכבת פונקציות, הקשר בין הגרף לנגזרת
כיתה: י' - יב'
שאלון: מבחן בגרות שאלון ראשון ברמת 5 יח"ל, 806- קיץ תשע"ו, מועד א'
תיאור:השאלה מתוך , מהווה בסיס לפעילות חקר והתנסות בעזרת יישומון בגאוגברה (להורדה).
בפעילות התלמיד מתבקש לחקור את הפונקציה באופן איכותני, כפונקציית חזקה מורכבת , ולהבחין בין חזקות זוגיות ואי זוגיות.
בפעילות גם הזמנה לתלמידים מתקדמים להמשיך ולבנות ולחקור.
נושא: תכונות הפונקציה- אנליזה
כיתה: מכיתה י והלאה
תיאור: יישומון זה מאפשר לקבוע אם פונקציה היא זוגית, אי-זוגית או שאינה זוגית ואינה אי-זוגית. היישומון נועד לשמש ככלי בשיח כיתתי העוסק במושגים: זוגיות של פונקציה ואי-זוגיות של פונקציה, ובמושגים נלווים כמו שיקוף בישר וסימטריה ביחס לנקודה. היישומון ניתן לשילוב גם בתוך פעילויות שמורים מחברים עבור כיתותיהם. דוגמה לשילוב היישומון בפעילות לתלמידים ניתן לראות בפעילויות פונקציה זוגית ואי- זוגית חלק א, חלק ב.
נושא: תכונות הפונקציה- אנליזה 
כיתה: י - י"ב
תיאור: בעליה להר תבור היכן המטפס נמצא במקום התלול ביותר?
דף עבודה ויישום דינאמי לחקירה של תכונת הקעירות כלפי מעלה וכלפי מטה.
מעקב אחר שיפוע המשיק ומיקומו מעל ומתחת לגרף תרמוז לנו על נקודת הפיתול.
כאן המקום לדון בקשר בין גרף הפונקציה לגרף הנגזרת הראשונה וכן גם הנגזרת השנייה.
נושא: תכונות הפונקציה- אנליזה
כיתה: י-י"ב
תיאור: יישום דינאמי בו ניתן להקליד פונקציה ולחקות את תהליך החקירה שלה.
ניתן לצפות שלב אחר שלב באיפיוני הפונקציה כגון נקודות אפס, נקודות קיצון, אסימפטוטות מקבילות לצירים ורק אז ליצור את הגרף.
ניתן גם להגדיר תחום סגור לפונקציה.
היישום נוצר על ידי רותם ינקלוביץ במסגרת קורס גאוגברה תשע"ג.
