המרכז הארצי למורים למתמטיקה בחינוך העל יסודי

הצטרפות למברק מתמטי

מדורי המרכז

תקציר| pdf אופניים ואופנוע| pdf מדריך למורה

בעקבות מבחן מפמ"ר תשע"ז

bike and bicycle capture Q

א. באיזו מהירות רכב רוכב האופנוע?

ב. איזה מרחק עברו רוכב האופניים ורוכב האופנוע עד שנפגשו?

מה היחס בין המרחקים שעברו? האם אפשר היה לדעת זאת מראש?

ג. אופיר טוען שאפשר לחשב את המרחק שעבר רוכב האופניים בלי לדעת את המהירות, בלי להתייחס לכך שהרוכבים נפגשו כעבור 3 שעות, ובלי לפתור שום משוואה. כיצד לדעתכם עשה זאת?

ד. יובל אמר: הבנתי.

אם המרחק ביניהם היה 5 ק"מ. רוכב האופנוע היה רוכב 4 ק"מ ורוכב האופניים בדיוק קילומטר אחד עד לפגישה. האם יובל צודק? הסבירו.

ה. היישומון אופניים ואופנוע מציג את התנועה של רוכב האופניים ורוכב האופנוע כתלות בזמן. היישומון מאפשר לקבוע את מהירות הרכיבה של רוכב האופניים (מהירות הרכיבה של רוכב האופנוע נקבעת בהתאם), ומאפשר לקבוע את הזמן שחלף מתחילת הרכיבה.

הסבירו את דבריהם של אופיר ויובל באמצעות היישומון.

Q5 bike and bycicle

ו. הציעו שאלה נוספת הקשורה לנתונים שאפשר לענות עליה בלי לפתור משוואה.

תקציר| pdf מלבן ופרבולה| pdf מדריך למורה

בעקבות מבחן מפמ"ר תשע"ז

rectangle and parabula Q

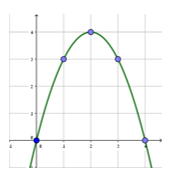
במערכת הצירים מסורטטים שני גרפים של פונקציות ריבועיות.
גרף אחד הוא של הפונקציה f(x) = x2 (מסומן ב-i ).

1. מי מבין הפונקציות הבאות לא יכולה להיות הפונקציה שהגרף שלה מסומן ב- ii? הסבירו. (יש יותר מאשר תשובה נכונה אחת)

rectangle and parabula capture (1) $g(x)=2x^2$

(2) $g(x)=x^2+4$

(3) $g(x)=3x^2$

(4) $g(x)=x^2-2$

(5) $g(x)=x^2+6$

(6) $g(x)=(x+2)^2$

2. נתון גם שהגרף המסומן ב- (ii) מתקבל מהגרף המסומן ב- (i) על ידי הזזה 4 יחידות למעלה.

א. מהם שיעורי נקודת הקדקוד של הפרבולה המסומנת ב- ii?

ב. כתבו את הביטוי האלגברי של הפרבולה המסומנת ((ii.

3. סרטטו מלבן שאחד מקדקודיו הוא ראשית הצירים וקדקוד נגדי לו הוא M(2,4). צלע אחת של המלבן על ציר ה- y (ראו סרטוט).

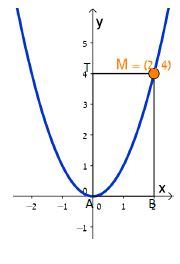
א. הסבירו מדוע נובע מהנתונים שלמלבן יש גם צלע המונחת על ציר ה- x.

ב. חשבו את שטח המלבן. הציגו דרך פתרון.

ג. איזו מבין המשוואות מתאימה לייצג את הישר
עליו מונח אחד מאלכסוני המלבן.

(1)y = 2x + 4 (2) y = –2x + 4
(3) y = x + 4 (4) y = –x + 4.

4. עדן בנתה (אפשר בעזרת היישומון) מלבנים נוספים ABMP, שאחד מקדקודיהם, M, נמצא על הפרבולה $y=x^2$ , ושני קדקודים שלהם על הצירים (ראו סרטוט).

bike and bicycle Q4

השלימו בטבלה מה שטח המלבן של כל אחד מהמלבנים שיצרה עדן.

		(3,__)	(2,4)	(1,1)	הנקודה M
			8 סמ"ר	1 סמ"ר	שטח המלבן

5. עדן שמה לב ששטח כל אחד מהם הוא $AB^3$ , כאשר $AB$ אורך הצלע המונחת על ציר ה- x. למשל: אם הקדקוד M הוא בנקודה (3,9), אורך הצלע $AB$ הוא 3 יחידות ושטח המלבן 27 יחידות. האם זה מקרי? הסבירו תוכלו להיעזר ביישומון.

6. עופר ואלון בנו מלבן שקדקוד אחד שלו על הפרבולה $y=x^2+4$ ,שתי צלעות שלו על הצירים ושתי צלעות מקבילות לצירים. הם סימנו ב- $x$ את הצלע המונחת על ציר ה- $x$ , וחיפשו ביטוי אלגברי לשטח המלבן כפונקציה של $x$ . עופר קיבל את הביטוי $x(x^2+4)$ , אלון קיבל את הביטוי $x^3+4x$ .

א. מי צודק? האם ייתכן ששניהם צודקים?

ב. כיצד חישב כל אחד מהם את שטח המלבן?

7. גם יעל בנתה מלבן עבור הפרבולה המוזזת $y=x^2+4$ , כאשר קדקוד אחד שלו על הפרבולה $y=x^2+4$ , שתי צלעות שלו על הצירים ושתי צלעות נוספות מקבילות לצירים. יעל חילקה אותו לשני מלבנים באופן שונה מאשר אלון.

סמנו ב- $x$ את הצלע המונחת על ציר ה- $x$ .

ניתן להיעזר ביישומון מלבן ופרבולה מוזזת.

א. הביעו בעזרת $x$ , את אורכי הצלעות של המלבן ABCD ואת שטחו.

ב. הביעו בעזרת $x$ , את אורכי הצלעות של המלבן PMCD ואת שטחו.

ג. הסבירו כיצד ניתן להביע את שטח המלבן של הפונקציה המוזזת ((ABCD כסכום שני מלבנים.

ד. האם קיים שוויון בין הביטויים שקיבלתם בסעיף א' לסעיף ג'? הסבירו שיקולכם.

תקציר|משולשים חסומים בפרבולה|מדריך למורה

triangle in parabola pic

פתחו את היישומון - משולשים החסומים בפרבולה, וענו על השאלות:

א. נתון גרף פונקציה ריבועית: $f(x)=-x^2+2x+8$

- מהן נקודות האפס של הפונקציה?

- מהו התחום בו הפונקציה אי שלילית?

- מהו ציר הסימטריה של הפרבולה?

ב. חוסמים משולש בפרבולה בתחום בו היא אי שלילית.

עקבו ביישומון אחר בניית המשולש החסום בפרבולה באמצעות סרגל הנווט, (צעדים 1-7).

הסבירו במילים שלכם את הבניה.

ג. הזיזו את הנקודה K ועקבו אחר משולשים שונים החסומים בפרבולה.

האם לדעתכם קיים משולש בעל שטח מינימלי? בעל שטח מקסימלי?

ד. נסמן את שיעור ה-x של הנקודה K ב-x.

בטאו באמצעות x את שיעורי הנקודות M, L ,K ובדקו ביישומון בסרגל הנווט, (צעדים 7-11).

ה. דן הציג את שטחי המשולשים באמצעות פונקציית המטרה $s(x)=\frac{1}{2}(x-1)(-x^2+2x+8)$

גרף הפונקציה של דן מוצג ביישומון בחלון השמאלי (צעד 12).

הסבירו את הביטויים האלגבריים בפונקציה של דן.

ו. הזיזו שוב את הנקודה K שעל הפרבולה.

בחלון הימני מופיעה נקודה כתומה P, המתאימה ל-x את שטח המשולש החסום בפרבולה. כאשר תזיזו את הנקודה K, תוכלו לעקוב אחר השתנות שטח המשולש. במה דומה הגרף שיצרו העקבות לגרף הפונקציה שבנה דן ובמה הוא שונה ממנה?

ז. יצד תגדירו את פונקצית המטרה למציאת השטח המקסימלי של המשולש MLK? חקרו את הפונקציה ומצאו לה שתי נקודות מקסימום. מהם המשולשים המתאימים?

ח. הסבירו באופן גאומטרי מדוע קיימים שני משולשים בעלי שטח מקסימלי.

תקציר| מדריך למורה

אוסף פעילויות זה מציג מספר בעיות קיצון מתפתחות. האוסף בנוי כמספר רצפי פעילויות, מלוות ישומונים לחקר והמחשה.

הפעילויות מיועדות לתלמידים ומבוססות על פעילויות מהספר "ללמוד וללמד אנליזה", שיצא לאור בשיתוף פעולה של המחלקה לחינוך למדע וטכנולוגיה בטכניון, מנהלת מל"מ ומשרד החינוך.

רצף הפעילויות	מקום בתוכנית הלימודים	הפעילות	נושאים
פינת חי מלבנית	כיתה י'	חצר מלבנית	חקירת פונקצית פולינום. מתאימה כפעילות פתיחה.
		חצר פינתית	חקירת פונקצית פולינום
		חצר מחולקת	חקירת פונקצית פולינום, חקירת פונקציה עם פרמטר. (מתאים להצמחת הצורך בשימוש בפרמטרים)
		עניין של מחיר	חקירת פונקצית פולינום, חקירת פונקציה עם פרמטר.
פינת חי משולשת	כיתות י - י"א	חצר משולשת	פונקצית שורש מורכבת.
פינת חי משולשת	כיתות י - י"א	משולש ישר זווית החסום במעגל	חקירת פונקציות טריגונומטריות. אפשר לעקוף בדרך גאומטרית את השימוש בחקירת פונקציות טריגונומטריות.
עם הפנים לנוף	כיתות י - י"א		חקירת פונקצית פולינום, חקירת פונקציה עם פרמטר. מגבלות התחום.
החופש בחירת המשתנה החופשי	כיתות י - י"א		חקירת פונקציות שונות, חקירת פונקציה עם פרמטר. בחירת המשתנה החופשי חושפת תכונות מסויימות של התופעה. מערכים שונים לעבודה בקבוצות

תקציר| pdf עבודת שורשים| pdf מדריך למורה

בעקבות בחינת הבגרות לתלמידי 4 יחידות – 35481 – קיץ תשע"ו – מועד ב - שאלה 6

roots work original Question

חלק א

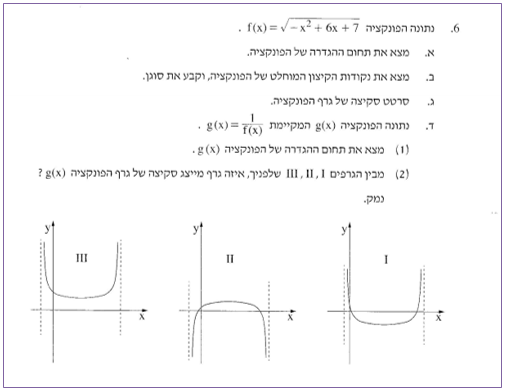
לפניכם גרף הפונקציה $h(x)=-x^{2}+4x+5$

1. מהו תחום ההגדרה של הפונקציה $f(x)=\sqrt{-x^{2}+4x+5}$ ?

2. מצאו את נקודות הקיצון המוחלט של הפונקציה f וקבעו את סוגן.

3. מה הקשר בין תחום העלייה של הפונקציה h לבין תחום העלייה של הפונקציה f? נסו להסביר את תשובתכם ביותר מאשר דרך אחת.

4. סרטטו באותה מערכת צירים את גרף הפונקציה $f(x)=\sqrt{-x^{2}+4x+5}$ .

היעזרו בנקודות המסומנות באדום. האם לכל אחת מהן יש נקודה מתאימה על גרף הפונקציה f?

5. על גרף הפונקציה h מסומנות בירוק שתי נקודות ששיעור ה- y שלהן הוא 1. הסבירו מדוע נקודות אלה נמצאו גם על גרף הפונקציה f?

(רמז: מה הקשר בין מספרים קטנים מ- 1 לבין השורשים הריבועיים שלהם?)

חלק ב

נתונה הפונקציה $g(x)=\frac{1}{\sqrt{-x^{2}+4x+5}}$

1.מהו תחום ההגדרה של הפונקציה g?

2. איזה מן הגרפים הבאים יכול לייצג סקיצה של גרף הפונקציה g? הסבירו.

roots work part B

חלק ג – סרטוט גרף של פונקציית שורש מורכבת בעזרת גרף הפונקציה הפנימית בלבד.

לפניכם גרף של פונקציה h.

נסרטט בעזרתו את גרף הפונקציה $f(x)=\sqrt{h(x)}$ : roots work part C

1. מהו תחום ההגדרה של הפונקציה f?

2. מצאו את נקודות הקיצון המוחלט של הפונקציה f וקבעו את סוגן.

4. סרטטו באותה מערכת צירים את גרף הפונקציה $f(x)=\sqrt{h(x)}$ . היעזרו בנקודות המסומנות.

חלק ד – הרחבת החקירה לפונקציות נוספות מהמשפחה $f(x)=\sqrt{h(x)}$ , כאשר h פונקציה ממעלה שנייה

היישומון שורשים מאפשר לסרטט גרפים של פונקציות שורש מורכבות, יחד עם פונקציה פנימית שהיא פונקציה ממעלה שנייה. משנים את הפרמטרים של הפונקציה הפנימית, והפונקציה המורכבת משתנה אף היא.

לנוחיות, נרשום את הפונקציה ממעלה שנייה בצורתה הקדקודית: $h(x)=a(x-m)^{2}+k$

1. באיורים שלפניכם גרף הפונקציה הפנימית מופיע בקו רציף, וגרף הפונקציה המורכבת מופיע בקו מרוסק. מצאו באמצעות היישומון פונקציות שיכולות להתאים לאיורים:

roots work part D1

roots work part D2 2. הסבירו מדוע אין אפשרות לקבל ביישומון את צירוף הגרפים הבא:

(הגרף המקווקו הוא של הפונקציה המורכבת והגרף הרציף הוא של הפונקציה הפנימית)

היעזרו בסעיף 5 של חלק א'.

תקציר| pdf חסומים במעגל| pdf מדריך למורה

in a circle part A נתון משולש PDC.

הנקודות B ו- L מונחות על הצלע PC.

הנקודות A ו- K מונחות על הצלע PD.

נתון כי המרובע ABLK בר חסימה וגם המרובע KLCD בר חסימה.

חלק א

חקרו את המרובע ABCD על פי הסעיפים הבאים, והסבירו את תשובותיכם:

אפשר להיעזר ביישומון

1. האם ABCD מקבילית? תמיד/ לפעמים/ אף פעם לא?

2. האם ABCD דלתון? תמיד/ לפעמים/ אף פעם לא?

3. האם ABCD טרפז? תמיד/ לפעמים/ אף פעם לא?

4. האם ABCD טרפז שווה שוקיים? תמיד/ לפעמים/ אף פעם לא?

5. האם ניתן לחסום את המרובע ABCD במעגל? תמיד/ לפעמים/ אף פעם לא?

חלק ב

נהפוך את נקודת המבט:

ABCD טרפז. L נקודה על הצלע BC ו- K נקודה על הצלע AD. היעזרו ביישומון.

1. האם KABL מקבילית? תמיד/ לפעמים/ אף פעם לא?

2. האם KABL דלתון? תמיד/ לפעמים/ אף פעם לא?

3. האם המרובעים ABLK ו- KLCD ברי חסימה? תמיד/ לפעמים/ אף פעם לא? הסבירו.

4. האם יתכן שרק אחד מהמרובעים ABLK ו- KLCD בר חסימה? הסבירו.

תקציר| pdf פירמידה משולשת| pdf מדריך למורה

במבט נוסף על בחינת הבגרות – 807 – חרף תשע"ז – שאלה 2

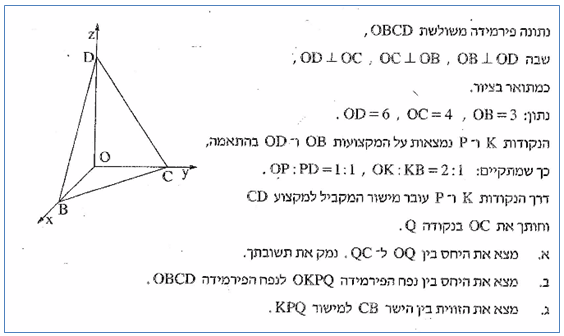
Tetrahedron the Question

נתונה פירמידה משולשת OBCD, קדדקוד O בראשית הצירים , והקדקודים B,C,D נמצאים על הצירים x,y,z בהתאמה.

א. רשמו על פי הנתונים את שיעורי הקדדקדים של הפירמידה.

ב. חשבו על פי חלוקת היחסים הנתונים את שיעורי הנקודות P, K.
בדקו את חישובכם ביישומון. הפעילו את הכלי "סיבוב הצגה תלת מימדית" בכדי להתרשם מהפירמידה במבטים שונים.

ג. דרך הנקודות K ו-P העבירו מישור המקביל למקצוע CD, וחותך את OC בנקודה Q. הציגו ביישומון את המישור המקביל והתבוננו בו במבטים שונים.

הסבירו מדוע PQ מקביל למקצוע CD. (תוכלו להיעזר בחלון הימיני התחתון)

ד. התבוננו במשולש OCD, מה ניתן לומר על הקטע PQ ?

ה. חשבו את היחס בין OQ ל-QC. נמקו תשובתכם.

מהם שיעורי הנקודה Q ?

ו. חשבו את יחס הנפחים.

ומה יקרה אם....

א. אם נזיז את הנקודה K ,

- האם וכיצד ישתנו שיעורי הנקודה Q ?

- האם המישור PQK עדיין מקביל ל-CD ?

- כיצד ישתנה יחס הנפחים?

ב. אם נזיז את הנקודהP ,

- האם וכיצד ישתנו שיעורי הנקודה Q ?

- האם המישור PQK עדיין מקביל ל-CD ?

- כיצד ישתנה יחס הנפחים?

ג. האם תוכלו להצביע על הבדל בין ההשפעה של השינוי במיקום הנקודה K ל נפח הפירמידה, לבין ההשפעה של השינוי במיקום הנקודה P על נפח הפירמידה?

ד. האם תוכלו לקבוע את הנקודות K ו-P כך שיחס הנפחים יהיה ? ? ?

אם לא, הסבירו מדוע. אם כן, כיצד? נמקו.

תקציר| pdf אל הפונקציה צעד אחר צעד| pdf מדריך למורה

אל משפחת הפונקציות $f(x)=\frac{x}{\sqrt{x^{2}-a^{2}}}$

א. נבחן צעד אחר צעד את שלבי הבנייה של משפחת הפונקציות $f(x)=\frac{x}{\sqrt{x^{2}-a^{2}}}$ , בעזרת פעולות והרכבה של פונקציות שונות.

לגבי כל אחת מהפונקציות הבאות, בכל שלב ענו, אם ניתן ללא שימוש בנגזרת. שימו לב, במעבר משלב לשלב אילו תכונות השתנו? אילו נשמרו?

		איזו פעולה הופעלה במעבר מהפונקציה הקודמת ?	מהו תחום ההגדרה?	אסימפטוטות מאונכות לצירים	האם הפונקציה זוגית? אי זוגית?	תחומי חיוביות ושליליות	תחומי עליה וירידה	סקיצה לגרף הפונקציה	סקיצה לגרף כאשר a=0
1	$y=x^{2}-a^{2}$	XXXXX
2	$y=\sqrt{x^{2}-a^{2}}$
3	$y=\frac{1}{\sqrt{x^{2}-a^{2}}}$
4	$y=\frac{x}{\sqrt{x^{2}-a^{2}}}$

ב. חקרו, את משפחת הפונקציות $f(x)=\frac{x}{\sqrt{x^{2}-a^{2}}}$ , צעד אחר צעד, באופן דומה לחקירה בסעיף א

ג. חשבו את הנגזרת של הפונקציה $f(x)=\frac{x}{\sqrt{x^{2}-a^{2}}}$ .

חקרו את משפחת הפונקציות $f'(x)$ , באופן דומה לחקירה שביצעתם בסעיף א.

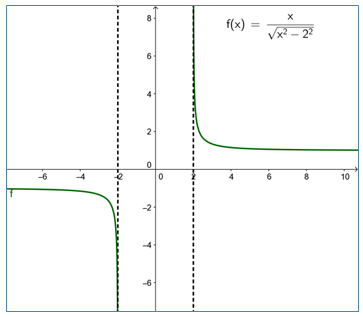
ד. לפניכם אחת הפונקציות מהמשפחה $y=\frac{x}{\sqrt{x^{2}-a^{2}}}$ כאשר a=2.

1. סמנו על הגרף את השטח המתואר ע"י הביטוי $\left | \int_{4}^{6}f(x)dx \right |$

2. סמנו על הגרף את השטח המתואר ע"י הביטוי $\left | \int_{-4}^{-6}f(x)dx \right |$

3. מצאו עבור $a>0$ את ערך הביוטי: $\int_{-3a}^{-2a}f(x)dx+\int_{2a}^{3a}f(x)dx$

ה. מצאו, עבור $a>0$ , את ערך הביטוי $\int_{-3a}^{-2a}f(x)dx+\int_{2a}^{3a}f(x)dx$ אם הפונקציה היא:

1. $f(x)=\frac{x}{\sqrt{x^{2}-a^{2}}}$

2. $f(x)=\frac{x3}{\sqrt{a^{2}-x^{2}}}$

תוכלו לבדוק את תשובתכם ביישומון סכום אינטגרלים.

ו. ללא חישובים מספריים הביאו דוגמה לפונקציה נוספת כך שעבור $a>0$ ערך הביטוי $\int_{-3a}^{-2a}f(x)dx+\int_{2a}^{3a}f(x)dx$ יהיה אפס.

תוכלו לבדוק את הדוגמה שלכם ביישומון סכום אינטגרלים

תקציר| pdf 1 האינטגרל כפונקציה| pdf 1 מדריך למורה

חקרתם את הפונקציה $f(x)=-3x^{2}e^{x^{3}}$ ואת הפונקציה $g(x)=\left | f(x) \right |$ וקיבלתם את הגרפים:

integral as a function

1. הסבירו מדוע $g(x)=-f(x)$ . כיצד תכונה זו מתבטאת בגרף?

2. השוו בין ערכי האינטגרל המסויים:

$I_{2}=\int_{- 1}^{0}g(x)dx , I_{1}=\int_{- 1}^{0}f(x)dx$ , אין צורך לחשב ערכים מספריים.

מה מייצג כל אינטגרל ? הסבירו.

3. נגדיר פונקציה $h(a)=\int_{- 1}^{0}f(x)dx$ .

תוכלו להיעזר ביישומון וגררו את הנקודה A, והתבוננו בחלון השמאלי.

א. על פי הגרף של $f(x)$ תארו כיצד משתנה $h(a)$ ככל ש- a גדל?

ב. באיזה תחומים, אם בכלל, הפונקציה $h(a)$ חיובית? שלילית?

ג. באיזה תחומים, אם בכלל, הפונקציה $h(a)$ עולה? יורדת?

ד. האם לפונקציה $h(a)$ יש נקודות קיצון? אם כן, מהן?

ה. שרטטו סקיצה לגרף הפונקציה $h(a)$ . מה מייצג הגרף?

ו. רשמו ביטוי אלגברי מתאים לפונקציה $h(a)$ .

סמנו עם העכבר את חלון הגרפי השני. רשמו ביטוי אלגברי עבור הפונקציה $h(x)$ בחלון הקלט (שימו לב יש לרשום את הביטוי כמשתנה של x ולא של a) ובדקו שהגרפים מתלכדים.

4. נגדיר פונקציה $t(a)=\int_{- 1}^{a}g(x)dx$ .

תוכלו להיעזר ביישומון וגררו את הנקודה A, והתבוננו בחלון השמאלי.

א. על פי הגרף של $g(x)$ תארו כיצד משתנה $t(a)$ ככל ש- a גדל?

ב. באיזה תחומים, אם בכלל, הפונקציה $t(a)$ חיובית? שלילית?

ג. באיזה תחומים, אם בכלל, הפונקציה $t(a)$ עולה? יורדת?

ד. האם לפונקציה $t(a)$ יש נקודות קיצון? אם כן, מהן?

ה. שרטטו סקיצה לגרף הפונקציה $t(a)$ . מה מייצג הגרף?

ו. רשמו ביטוי אלגברי מתאים לפונקציה $t(a)$ .

סמנו עם העכבר את חלון הגרפי השני. רשמו ביטוי אלגברי עבור הפונקציה $t(x)$ בחלון הקלט (שימו לב יש לרשום את הביטוי כמשתנה של x ולא של a) ובדקו שהגרפים מתלכדים.

5. השוו בין הפונקציות $h(a)$ ו- $t(a)$ . במה דומים ובמה שונים הגרפים שלהם?

מהי נקודת החיתוך בין הגרפים?

הרחבה:

6. אם נשנה את הגבול התחתון של האינטגרל $h(a)=\int_{- 0.5}^{a}f(x)dx$ ,

כיצד לדעתכם ישתנה גרף הפונקציה $h(a)$ ? כיצד ישתנה הביטוי האלגברי של הפונקציה?
הסבירו מסקנתכם.

הזיזו ביישומון את הנקודה B וקבעו אותה כך ש- $x=-0.5$ , גררו את הנקודה A ועקבו אחר בניית הגרף של $h(a)$ .

במקרה זה, היכן יפגשו הגרפים $h(a)$ ו- $t(a)$ ?

בדקו מסקנתכם עבורי ערכי גבול תחתון שונים.

7. חקרו כיצד ישתנו ממצאיכם עבור הפונקציות:

א. $f(x)=x^{3}-x$ ו- $g(x)=\left | f(x) \right |$

ב. $f(x)=x^{3}-x$ ו- $g(x)=-f(x)$

שערו ובדקו ביישומון היכן יפגשו הגרפים $h(a)$ ו- $t(a)$ ? נמקו.

תקציר|המתמטיקה של התרופות

לפניכם גרף המתאר התפרקות אופיינית של האינסולין בדם מהרגע שנלקחה התרופה.

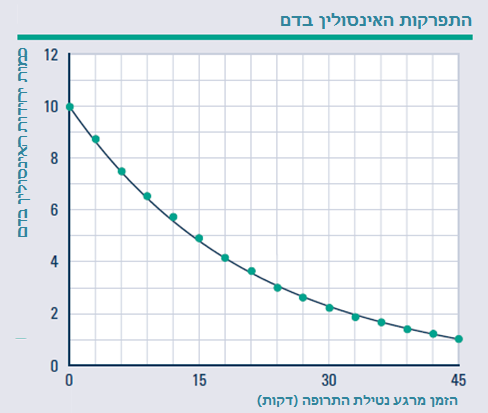
1. השלימו את הטבלה:

2. תארו במילים את התפרקות האינסולין בדם כתלות בזמן. תארו את קצב השינוי.
3. בהתבסס על הגרף והטבלה איזו פונקציה מתארת התפרקות האינסולין בדם כתלות בזמן?

4. חשבו על פי הפונקציה ובדקו בגרף.
א. כמה אינסולין נותר בדם לאחר שעה?
ב. כמה יחידות אינסולין בדם לאחר שעה וחצי?
ג. לאחר כמה זמן נותר בדם חצי מהכמות ההתחלתית של האינסולין?
ד. לאחר כמה זמן נותר בדם חצי יחידה של אינסולין?

בפתרון השאלות הבאות תוכלו להיעזר ביישומון:

1. ד"ר פאר רשם לחולה מסויים כדורי טריאזולם. לאחר שהחולה נטל מספר גלולות,
היתה בדם של החולה כמות התחלתית של 4 מיליגרם.
א. מה תהיה כמות הסם בדם לאחר שעה? לאחר 6 שעות? לאחר יממה?
ב. במשך כמה שעות תעלם השפעת הסם ?
ג. בדיקת דם מסוגלת לאבחן נוכחות של התרופה אם תמצא בדם כמות של לפחות 0.1 מיליגרם מהתרופה.
לאחר כמה זמן תתקבל בדיקה שלילית?
2. א. שרטטו גרף לכל תרופה.
ב. השוו את השפעת ארבעת הסמים וסכמו את מסקנותיכם בכל ייצוג שתבחרו. מה ניתן לומר על קצב ההתפוגגות של כל תרופה.
ג. רק שלש מן הגלולות הן אמיתיות, הצביעו על גלולת השינה הלא אמיתית ונמקו תשובתכם.
3. רופאים מתעניינים בזמן שלוקח לתרופה בדם להגיע לחצי מהכמות ההתחלתית שניטלה. זמן זה נקרא מחצית החיים.
חשבו מהו זמן מחצית החיים של כל תרופה.

הפעילות מעובדת מתוך – פעילויות חקירה תמוכות מחשב – פונקציה מעריכית ולוגריתמית – אוניברסיטת חיפה.

מקורות נוספים:

הסכנות באקמול – שיעור אינטראקטיבי לחקר השאלה מה קורה שלוקחים תרופת האקמול לכאב ראש בכמויות שונות ובזה אחר זה.

יישומונים ופיצוחים בנושא גידול ודעיכה:

אני ואתה נשנה את העולם – פיצוח העוסק בפונקציה המעריכית דרך סרט הקולנוע "העבר את זה הלאה".
דעיכה רדיואקטיבית - סימולציה לדעיכה רדיואקטיבית. ישומון דינאמי ודף עבודה בו ניתן לחקור כיצד משפיעים הפרמטרים השונים של פונקצית הדעיכה על הגרף הן בייצוג הגרפי, הטבלאי והויזואלי. כמו כן ניתן לעקוב אחר ערכים של הפונקציה.וכן להתרשם מקצב הדעיכה באנימציה של המיכל המתרוקן.
מרוב עצים לא רואים את היער...סימולציה לגידול מעריכי של יער ישומון דינאמי ודף עבודה בו ניתן לחקור כיצד משפיעים הפרמטרים השונים של פונקצית הגידול על הגרף הן בייצוג הגרפי, הטבלאי והויזואלי. כמו כן ניתן לעקוב אחר ערכים של הפונקציה .וכן להתרשם מקצב הגידול באנימציה של היער הגדל.
עלייה במחירי הדירות – הפעילות כוללת דף עבודה ויישומון דינאמי, ועוסקת בהשוואה בין עליה של המחירים של שתי דירות בגידול מעריכי.