מדורי המרכז
תקציר|![]() אינטגרל של פונקציה זוגית ואי זוגית|
אינטגרל של פונקציה זוגית ואי זוגית|![]() מדריך למורה
מדריך למורה
ניתן להיעזר ביישומון
1. נתון גרף הפונקציה (f(x בתחום בו x חיובי.
א. השלימו את הגרף כך ש-f(x) תהיה פונקציה אי זוגית.
הסבירו מהי התכונה האלגברית של פונקציה זוגית ומה משמעותה הגאומטרית בגרף.
ב. נתון כי: . הביעו אם אפשר בעזרת S את ערך האינטגרל:
1.
2.
ג. נתון כי: . הביעו אם אפשר בעזרת A את ערך האינטגרל:
1.
2.
3.
2. נתון גרף הפונקציה בתחום בו x חיובי.
א. השלימו את הגרף כך ש-f(x) תהיה פונקציה זוגית.
הסבירו מהי התכונה האלגברית של פונקציה זוגית ומה משמעותה הגאומטרית בגרף.
ב. נתון כי: . הביעו אם אפשר בעזרת S את ערך האינטגרל:
1.
2.
ג. נתון כי: . הביעו אם אפשר בעזרת A את ערך האינטגרל:
1.
2.
3.
3. נתונה הפונקציה ונתון הגרף שלה.

א. הראו כי (f(x אי זוגית.
ב. הסבירו מדוע
ג. האם נכון לומר כי ?
ד. חשבו . נמקו.
היעזרו בתכונת המחזוריות של הפונקציה.
4. נתונה הפונקציה
א. הראו כי .
ב. סרטטו סקיצה לגרף (g(x.
ג. חשבו את האינטגרל .
חשבתם פעם לבנות עץ ממשפט פיתגורס?


הכירו את הפקרטל עץ הפיתגורס, הנוצר בסדרה אינסופית של ריבועים הדומים לעצמם בכל רמת פירוט שנסתכל בה. לתכונה זו קוראים, "דמיון עצמי" ,כלומר כל חלק של הפרקטל נראה כמו השלם, החלק של החלק נראה כמו החלק וכך הלאה..... כל ריבוע בעץ פיתגורס יוצר גרסה מוקטנת של עץ פיתגורס בעצמו.
בשלב האפס מתחילים עם ריבוע עם צלע באורך 1.
בשלב הראשון בונים שני ריבועים זהים כך שהם יוצרים משולש ישר-זווית ושווה שוקייםעם צלע הריבוע ההתחלתי.
א. מה אורך צלע הריבועים האלה?
בשלב השני בונים על גבי כל אחד מן הריבועים האלו שני ריבועים זהים באותו אופן בדיוק.
ב. מה אורך צלע הריבועים בשלב השני?
כמה ריבועים בשלב השני?
ג. מה ניתן לומר על המשולשים מהשלב הראשון והשני?
עץ פיתגורס מתקבל מחזרה על התהליך אינסוף פעמים.
ד. מה אורך צלע הריבועים בשלב ה-n?
כמה ריבועים יהיו בשלב ה-n?
ה. כיצד יראה עץ פיתגורס אם נתחיל ממשולש ישר זווית שאינו שווה שוקיים?
התנסו ביישומון עץ פיתגורס.
ו. אתגר - ניתן להראות שניתן לחסום את עץ הפיתגורס במלבן.
מצאו מה השטח האפשרי המינימלי למלבן כזה.
הצעה לפרוייקט – בנו קיר לכבוד חג האילנות, עץ פיתגורס פורח.

ראו צעד אחד כיצד כיתה בספרד בנתה את עץ פיתגורס באתר משחקים טופולוגיים (בספרדית).
מצורפים (למטה) תבניות להדפסה.
מקורות נוספים:
עץ פיתגורס - יישומון בגאוגברה.
הפיצוח – אני דומה לעצמי

הנקודות E, F מונחות על הצלעות AB, DC בהתאמה.
EB = FD
ניתן להיעזר ביישומון המקבילית.
1. מה ניתן לומר על המרובע AECF ? הוכיחו טענתכם בדרכים שונות.
א. האם המרובע AECF מקבילית? תמיד/ לפעמים / אף פעם לא.
ב. האם המרובע AECF טרפז? תמיד/ לפעמים / אף פעם לא.
ג. האם המרובע AECF מעוין? תמיד/ לפעמים / אף פעם לא.
ד. האם המרובע AECF מלבן שאינו ריבוע? תמיד/ לפעמים / אף פעם לא.
ה. האם המרובע AECF מלבן ? תמיד/ לפעמים / אף פעם לא.
ו. האם המרובע AECF ריבוע ? תמיד/ לפעמים / אף פעם לא.
3. הראו כי שלש הנקודות B, O, D נמצאות על ישר אחד.
(רמז – הראו כי BD עובר דרך הנקודה O).
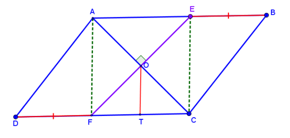
א. הוכיחו:
ב. שנו ביישומון את הזווית , כך שלא בהכרח תהיה ישרה.
האם עדיין נשמר הקשר ?
נמקו.
5. מצאו כמה שיותר מצולעים בעלי שטחים שווים.
תקציר|![]() כדאי להזיז את הפונקציה|
כדאי להזיז את הפונקציה|![]() מדריך למורה
מדריך למורה
נתונה הפונקציה . a הוא פרמטר.
1. יעל הציעה לחקור פונקציה פשוטה יותר
ובעזרת הזזות בלבד להסיק מסקנות לגבי הפונקציה הנתונה.
א. השלימו את הטבלה, תוכלו להיעזר ביישומון הדינאמי.
ב. ציינו מה דומה ומה שונה בין שתי הפונקציות? אילו תכונות נשמרו ואילו תכונות השתנו וכיצד?
ג. כיצד תשתנה הפונקציה כאשר נשנה את a ?
אילו תכונות נשמרו ואילו תכונות השתנו וכיצד?
ד. עבור איזה ערך של a, משיקה לציר ה-x ? נמקו.
2. נתונה הפונקציה עבור a=1, k פרמטר.
לפניכם ארבעה גרפים שונים ממשפחת הפונקציות g(x).
(בקו המקווקו מוצג גרף הפונקציה f(x)+k )
תוכלו להיעזרביישומון הדינאמי- הערך המוחלט של פונקציה מוזזת.
א. קבעו עבור אילו ערכי k ניתן לקבל כל אחד מהגרפים. נמקו.
ב. הוסיפו לגרפים את הישר שהוא האסימפטוטה של f(x).
באילו מקרים גרף הפונקציה g(x) ישיק לישר זה? הסבירו.
תקציר | ![]() חזקה ונתחזק | פתרונות | חזקה ונתחזק בערבית | حلول
חזקה ונתחזק | פתרונות | חזקה ונתחזק בערבית | حلول
1. א. התוכלו לחשב את המספר: 
ב. אם תשנו את סדר החזקות, איזה מספר יהיה הגדול ביותר? הקטן ביותר?
המקור: NRICH - enriching marhematics
2. מה היא ספרת האחדות של המספרים: 
המקור: ומדאת פי אלריאדיאת גיליונות לשיפור החשיבה המתמטית, 2006
3. מה היא השארית המתקבלת כאשר מחלקים 32008 במספר 7?

המקור: NRICH - enriching marhematics
4. א. האם המספר 3444 + 4333 מתחלק ב- 5?
ב. התוכלו להסביר למה 599 +499 + 399+ 299 + 199 מתחלק ב- 5?
המקור: NRICH - enriching marhematics
5. נתון (בשנת 2008): a2 + a + 1 = 0
התוכלו לחשב את הביטוי a2008 + a2009?
המקור: ד"ר עוזי ערמון - חידות ובעיות חשיבה במתמטיקה

לפניכם תמונה של הר תבור הנמצא בלב הגליל התחתון, הידוע בכיפתו העגולה הנשקפת למרחקים. הוא מתנשא לגובה של 562 מטרים, כ-400 מטרים מעל פני סביבתו.
ביישומון, על קו המתאר שלו משורטטת באדום פונקציה המתאימה את קו הגובה בק"מ למרחק האופקי מנקודת המוצא בק"מ.
עזרו לטייל להכיר את המעלה, היכן הוא יוכל לנוח, היכן הוא הכי יתאמץ ?
ענו על השאלות הבאות:
1. הציגו את הטייל והזיזו אותו. עקבו אחר מסלול הטיפוס שלו לפסגה (מסומן באדום) ותארו במילים שלכם את מהלך הטיפוס. קבעו (אם אפשר):
■ היכן במעלה, העלייה היא התלולה ביותר?
■ היכן במעלה, העלייה היא הכי פחות תלולה?
■ היכן במעלה, העלייה הולכת ונהיית יותר ויותר תלולה?
■ היכן במעלה, העלייה הולכת ונהיית פחות ופחות תלולה?
2. הציגו את שיפוע המדרון.
עקבו אחר מיקום המשיק בנקודות שונות ביחס לגרף הפונקציה ומצאו:
■ הפונקציה קעורה כלפי מטה (∩):
תחומים בהם המשיק נמצא מעל הפונקציה. מה המשמעות לכך בסיפור?
■ הפונקציה קעורה כלפי מעלה (U):
תחומים בהם המשיק נמצא מתחת לפונקציה. מה המשמעות לכך בסיפור?
3. הציגו את שיפוע המדרון, עקבו אחר השינוי בשיפוע המשיק.
קבעו מהי המשמעות לכך בגרף הפונקציה, ומהי המשמעות לכך בסיפור עבור התנאים הבאים:
■ נקודות בהן שיפוע המשיק אפס.
■ נקודות בהן שיפוע המשיק שלילי.
■ נקודות בהן שיפוע המשיק חיובי.
■ תחומים בהם שיפועי המשיקים הולכים וגדלים .
■ תחומים בהם שיפועי המשיקים הולכים וקטנים.
4. עקבו אחר השיפוע. מוצגת נקודה B המתארת את גודל שיפוע המשיק בנקודה A.
■ מה מתאר גרף העקבות של הנקודה B? מה המשמעות לכך בסיפור ?
■ מה המשמעות בגרף הפונקציה לנקודות החיתוך של פונקצית השיפועים עם ציר ה-x? והמשמעות בסיפור?
■ מה המשמעות בגרף הפונקציה לתחומי החיוביות והשליליות של פונקצית השיפועים? והמשמעות בסיפור?
5. הצג פתרון- היכן המדרון הוא התלול ביותר?
■ מה מאפיין את המשיק בנקודת הפתרון?
■ הסבירו מה מייצג כל גרף בפתרון?
■ הסבירו מה מייצגת כל נקודה משלוש הנקודות המודגשות על הגרפים.
■ אילו תנאים בנגזרת הראשונה ובנגזרת השנייה מתקיימים בפתרון?
|
6. מלאו את הטבלה:
|
||||||||||||||||||||||||||||||||||||||||
תקציר|![]() שלוש פרבולות ולהן שלוש פונקציות קדומות|
שלוש פרבולות ולהן שלוש פונקציות קדומות|![]() חומר למורה
חומר למורה
לפניכם שלוש פרבולות "מחייכות"
1. שלוש הפרבולות הללו הן נגזרות של פונקציות אחרות כך ש:
- מהם תחומי העלייה והירידה של הפונקציות?
- סרטטו דוגמאות אפשריות לגרפים של פונקציות ,
ו-
.
- במה דומות ובמה הן שונות?
2. לכל אחת מן הפונקציות חקרו את תחומי הקעירות וציינו את מספר נקודות הפיתול של הפונקציה. הסבירו במה דומות ובמה שונות הפונקציות?
3. לכל אחת מן הפונקציות העריכו את מספר נקודות הפיתול של הפונקציה ואת שיפוע המשיק שם. הסבירו לפיכך במה דומות ובמה שונות הפונקציות?
4. סרטטו 3 פרבולות בעלות מקסימום ואת הפונקציות הקדומות שלהן:
(1) לפרבולה שתי נקודות חיתוך עם ציר ה- x.
(2) לפרבולה נקודת חיתוך אחת עם ציר ה- x.
(3) פרבולה ללא נקודות חיתוך עם ציר ה- x.
5. האם הגרפים של הפונקציות הבאות יכולים לייצג פונקציות ממעלה שלישית? הסבירו.
אם כן, ציינו על הגרף היכן נקודות הפיתול ושרטטו את המשיק שם.
הפעילות עובדה על פי:
"פונקציה ממעלה שלישית בתמונה משפחתית", ללמוד וללמד אנליזה, פרק 9, ע"מ 209
תקציר|![]() צביעת שני משולשים|
צביעת שני משולשים|![]() חומר למורה
חומר למורה

א. נצבע את המשולש החל מקודקוד A, עם משולש ישר זווית דומה לו (ADE) כאשר הנקודה D נעה על הצלע AB.
נסמן את אורך AD=x
הזיזו ביישומון את הנקודה D, ותארו כיצד משתנה השטח הצבוע כאשר x משתנה.
נגדיר פונקציה S(x) המתאימה ל- x את השטח הצבוע. האם פונקציית השטח הצבוע עולה? תארו את קצב ההשתנות שלה.

נצבע את המשולש החל מקודקוד B', עם טרפז (B'C'LK) כאשר הנקודה K נעה על הצלע A''B.
נסמן את אורך B'K'=x
הזיזו ביישומון את הנקודה D, ותארו כיצד הפעם משתנה השטח הצבוע כאשר x משתנה.
האם פונקציית השטח הצבוע עולה? תארו את קצב ההשתנות שלה.
ג. תארו מתי השטחים הצבועים בשני המשולשים יהיו שווים.
ד. חשבו את השטחים הצבועים בשני המשולשים, כאשר D אמצע הקטע AB ,
ו- K אמצע הקטע A'B' .
ה. חשבו את השטחים הצבועים בשני המשולשים, כאשר X=2.
ו. היעזרו ביישומון לשם חישוב השטחים ומלאו את הטבלה:
| X=6 | X=5 | X=4 | X=3 | X=2 | X=1 | X=0 | |
| שטח צבוע במשולש 1 | |||||||
| שטח צבוע במשולש 2 |
ז. עקבו ביישומון אחר בניית הגרף המתאר את השתנות השטח הצבוע כפונקציה של x, בכל אחד מהמשולשים.
במה דומים ובמה שונים שני הגרפים?
ח. שערו כיצד נראה גרף הנגזרת של פונקצית השטח בכל אחד מהמקרים?
ט. רשמו פונקציה המתארת את השתנות השטח הצבוע כאשר x משתנה עבור כל אחד מהמשולשים. הקלידו בחלון הקלט ובדקו תשובתכם.
גזרו את הפונקציה ובדקו השערתכם.
תקציר| ![]() היכן לקנות את הפיצה?|
היכן לקנות את הפיצה?|![]() חומר למורה
חומר למורה
1. בפסטיבל מדברי גדול התמקמו שתי פיצריות במרחק 6 ק"מ זו מזו, והן מספקות על גמלים פיצות לכל דורש. הפיצריות זהות בתפריט, באיכות ובמחיר הפיצה, וכל אחת מהפיצריות גובה שקל אחד לק"מ דמי משלוח.
א. היכן תקנו את הפיצה (התייחסו למקומות שונים בהם אתם יכולים להימצא?
ב. היכן נמצא קו פרשת הפיצה – קו התפר בין האזור שבו עדיף לקנות מפיצרייה א לבין האזור בו עדיף לקנות מפיצרייה ב?
ג. תוכלו לחקור את הבעיה באמצעות היישומון היכן לקנות את הפיצה. קבעו את יחס המחירים בין הפיצריות ל- m=1. תוכלו להגדיל ולהקטין את המרחק מהפיצרייה השנייה (). כדי לראות היכן נמצאות כל נקודות החיתוך בין העגלים, השתמשו באופציה "הפעל עקבות".
2. כיצד ישתנה קו התפר בין אזורי השיווק של הפיצריות, אם פיצרייה א תמשיך לגבות 1 ₪ לק"מ דמי משלוח ואילו פיצרייה ב תעלה את דמי המשלוח ותגבה 2 ₪ לק"מ דמי משלוח?
כדי לחקור אפשרות זו שנו את היחס בין מחירי המשלוח ל- m=2. בהתאם ישתנה גם היחס בין הרדיוסים של המעגלים (מדוע?)
3. אתם מוכנים להמשיך ולחקור את הבעיה לכל בין דמי המשלוח, וכן למצוא את הפתרונות גם בדרך אלגברית. לנוחיותכם, וכדי שהפתרון שלכם יתאים ליישומון, מקמו את הפיצרייה המשנה מחירים בראשית הצירים, ואת הפיצריה הגובה שקל אחד לק"מ מקמו בנקודה (6,0).
תקציר|![]() גלו את ההוכחה|
גלו את ההוכחה|![]() חומר למורה
חומר למורה
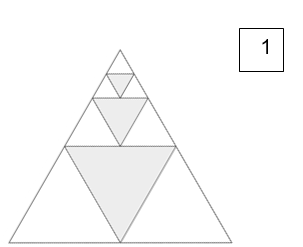
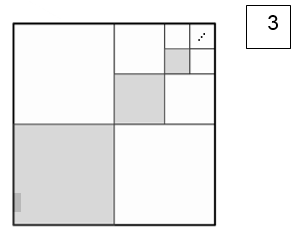
בכל אחד מן הסרטוטים מסתתרת הוכחה לנוסחה הקשורה לסכומי סדרות.
גלו את ההוכחה המסתתרת בכל סרטוט.
| |
|
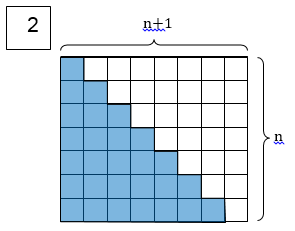 |
 |
 |
 |
 |
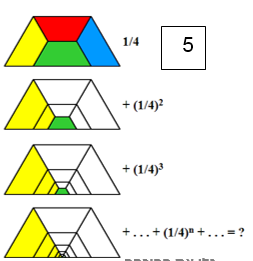 |
בדיוק או בערך
בחרו את התשובה המדויקת ביותר בעיניכם
1.
א. . ב. קצת יותר מ-
. ג. . קצת פחות מ-
. ד. מתלבט/ת
א. 1. ב. קצת יותר מ- 1. ג. קצת פחות מ- 1 . ד. מתלבט/ת.












