| תחום מספרי | תחום גאומטרי | תחום אלגברי | כיתה |
|
|
ז' | |
|
|
ח' | |
|
ט' |
תיאור: פעילות פתיחה לשיעור בנושא ביטויים אלגבריים המתייחסת להיקפים ושטחים של מלבנים - חלקת דשא ובריכה. הפעילות עוסקת מבחינה אלגברית בכינוס איברים דומים. מוצעות למשימה שלוש גרסאות (גרסה מצומצמת 1, גרסה מצמצמת 2 וגרסה למתקדמים) כך שניתן להשתמש בה בכיתה ז' הטרוגנית, או בחלוקה לרמות שונות.
מקור: Minutephysics
אופי הפעילות: יישום דינאמי.
תיאור: סרטון קצר הממחיש את חוק הפילוג מנקודת מבט אנרגטית ומבדרת.
 מקור:
מקור: תאור: שאלונים עם ביטויים אלגברים מסוגים שונים ברמות שונות לפישוט, עם משוב אינטראקטיבי. מתאים לתרגול ולבחינה עצמית.

מקור: משימות אוריינות
אופי הפעילות: יישום דינאמי דף עבודה.
תיאור: יישום דינאמי המציע חקר וגילוי במשימה האוריינית דרגשי העץ. המשימה מיועדת לכיתה ז ומשלבת את התחום האלגברי והגיאומטרי על תכונות המלבן והריבוע כולל שטח והיקף.
היישומון מלווה בשאלות אינטראקטיביות.
יישומון דרגשי העץ בהפקת אלנט עבור אגף טכנולוגיות מידע במשרד החינוך.
תיאור: הפעילות המוצעת מכילה משוואות מסוגים שונים, ומשימות מיון שלהן, כמו גם בעיות מילוליות קצרות ומשימת מיון שלהן. משימות המיון מזמנות התבוננות לאחר מעשה, כלומר לאחר הפיתרון, ובכך מאפשרות את העמקת ההבנה. במשימה 3 חלקים. ניתן להפעילם ב-3 שיעורים שונים. שני החלקים הראשונים עוסקים במיון משוואות, החלק השלישי עוסק במיון בעיות מילוליות פשוטות, הנפתרות באמצעות משוואות פשוטות.
 מקור: שאלות לדוגמה ממבחני פיזה. בתרגום: ראמ"ה
מקור: שאלות לדוגמה ממבחני פיזה. בתרגום: ראמ"ה
 מקור: מטח
מקור: מטח מקור: flashymaths
מקור: flashymaths
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: תרגול אינטראקטיבי לפתרון משוואות פשוטות ממעלה ראשונה. בכל שלב באפשרותך לבחור איזו פעולה יש להפעיל על כל אחד מאגפי המשוואה ולצפות באופן דינאמי וממחיש בתוצאה. התהליך ממשיך עד לפתרון המשוואה.
להפעלה אנא הסירו חסימת Flash מדריך הסרת Flash
 מקור: National Library of Virtual Manipulatives
מקור: National Library of Virtual Manipulatives
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: יישום אינטראקטיבי לפתרון משוואות במודל המלבנים.

מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: בפעילות מוצגים טריקים שונים לכפל מספרים בעזרת האצבעות שמהן יוכלו ליהנות תלמידים צעירים והבוגרים שביניהם יוכלו גם לחקור מהו הקסם המתמטי העומד מאחורי טריקים אלו. בפעילות זו אתם מתבקשים לצפות בסרטים המציגים את הטריקים, להוכיח באופן אלגברי (או אחר) מדוע השיטות הללו עובדות, להרחיב ולהכליל אותן. ניתן לשלב פעילויות אלו בפרק של בעיות מספרים.

מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: פתרון משוואות לינאריות פשוטות בעזרת המחשה ויזואלית וידידותית. נפתור משוואות בעזרת שימוש במודל המלבנים, שהכרנו בפיצוח "בארץ יצורי הפרא המתמטיים" להצגת מספרים שליליים. הפיצוח כולל סרטוני וידאו המציגים את המודל, יישומון דינאמי וכן דפי עבודה עצמית לתלמיד. ניתן לשלב בשימוש הלוח החכם.

אופי הפעילות: משחק אינטראקטיבי
תיאור: משחק לניחוש המיקום של הצוללות במערכת הצירים תוך שימוש בתוכנה Desmos. ניתן לשחק בזוגות בשני מכשירים ניידים. המשחק במערכת Desmos Teacher, ניתן להגדיר כיתה ולעקוב אחר התוצאות של התלמידים.

תיאור: פעילות כיתה בדסמוס לפיתוח המיומנות של סימון תחומים לפי אי שוויון על ציר המספרים.
 מקור: NGFL-cymru
מקור: NGFL-cymru
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: שני משחקים לשני שחקנים (או לשתי קבוצות בכיתה), במשחק הראשון יש לתת שיעורי נקודות כך שלא יווצר ישר העובר דרך שלש נקודות. במשחק השני יש ליצור כמה שיותר ריבועים.
 מקור: flashymaths
מקור: flashymaths
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: משחק אינטראקטיבי בו עליך לתפוס , תוך 30 שניות, את החייזרים המפוזרים במערכת הצירים, כאשר נתונים לך שיעורי הנקודות.
 מקור: Great MathTeaching Ideas
מקור: Great MathTeaching Ideas
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: הצעה לפעילות יצירתית בה מגרילים שיעורי נקודות ויוצרים יצירת אמנות. מלווה בסרטון הסבר ובדף פעילות.
 מקור: מתמטיקה עמקים תבור
מקור: מתמטיקה עמקים תבור
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: המלצות למשחקים אינטראקטיביים ברשת לתרגול והכרת מערכת הצירים.
 מקור: מתמטיקה עמקים תבור
מקור: מתמטיקה עמקים תבור
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: מצגת מאת מירטה לוין, המציעה משחק כיתתי לתרגול הנושאים שנלמדו בשליש הראשון של כיתה ז.
תיאור: הפעילות מתאימה לתלמידי כיתה ז' ו-ח' בקבוצות הגבוהות. במהלך פתרונה התלמידים מתמודדים עם פענוח מידע ופירוש של נתונים ונדרשים להמרות בין ייצוגים, תוך שימוש בשיקולים ובמיומנויות המתמטיות הבאות: חיבור וחיסור מספרים מכוונים, ערך מוחלט של מספר מכוון, הבנה של המושג 'מרחק נקודה מישר' וההבדל בינו לבין מרחק בין שתי נקודות, קריאת נתונים מתוך גרף, זיהוי המשמעות של הנתונים, בניית גרף, חשיבה והנמקה.
 מקור: Desmos Teacher
מקור: Desmos Teacher
אופי הפעילות: בפעילות האינטראקטיבית סרטוני וידאו קצרצרים והתלמידים חוקרים את הקשר בין הסיטואציה המתוארת בוידאו למודל המתמטי שלה.
תאור: בפעילות יש לתאר את ההשתנות על ידי שרטוט במערכת הצירים תוך שימוש בתוכנה Desmos. הפעילות במערכת Desmos Teacher, ניתן להגדיר כיתה ולעקוב אחר תהליך העבודה של התלמידים.
 אופי הפעילות: פעילות אינטראקטיבית מאת Desmos בה חוקרים את הגרף של מילוי כדים שונים לצד סימולציה.
אופי הפעילות: פעילות אינטראקטיבית מאת Desmos בה חוקרים את הגרף של מילוי כדים שונים לצד סימולציה.
תיאור: ראשית התלמידים מתנסים בשרטוט גובה פני המים בכד לפי הזמן. הם יכולים להשוות בסימולציה את הגרף שלהם ושל הכד. לאחר שהצליחו הם יכולים לשרטט כד משל עצמם ולתת לשאר התלמידים כאתגר – כיצד יראה הגרף עבור הכד שיצרו.
 מקור: Dan Meyer
מקור: Dan Meyer
אופי הפעילות: פרוייקט מאת dan meyer בו סרטונים קצרים המתארים סיטואציות שונות מהחיים, סיפור קצר כגון ניפוח בלון, כדור מתגלגל, סיבוב בקרוסלה.
תיאור: על התלמידים לצפות בסרטונים, לתאר ולהבין את הסיטואציה הנתונה, ולהרכיב גרף מתוך הנתונים בסרטון. ראו הרצאה מומלצת של TED כיצד מציע דן מאייר לעשות שינוי בכיתת המתמטיקה.
 מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
אופי הפעילות: דף עבודה ויישום דינאמי המבוססים על שאלה 21 בשאלון 801.
תיאור: ביישום מושם דגש על השיפועים השווים בגרף. יש אפשרות לשנות את השיפועים ולבדוק כיצד משתנה קצב גדילת השיער.
 מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
אופי הפעילות: דף עבודה ויישום דינאמי לחקירת ההתאמה בין הפונקציה של שטחים בצורות שונות המתמלאים בצבע לפי הזמן, לבין הגרפים שלהם. ניתן לדון באופי השונה והדומה של קצב השתנות הפונקציות.
 מקור: שיתוף פעולה בין Desmos ו- Dan Meyer
מקור: שיתוף פעולה בין Desmos ו- Dan Meyer
אופי הפעילות: אפליקציה מהנה העוסקת בבניית גרפים המתארים מצבים מהמציאות.
תאור: צפו באנימציות של אירועים בלונה פארק, מכוניות מתנגשות, צנחן, מסלול של רכבת הרים. שרטטו את הגרף של השתנותהגובה או המהירות. ניתן לראות סימולציה של הגרף שלכם לעומת האנימציה הנתונה. מצורף גם מדריך למורה.
תיאור: הפעילות מזמנת חיפוש חוקיות בסדרות של מבנים גיאומטריים, מדגישה את המגוון הרחב של נקודות המבט ותומכת בפיתוח ההבנה של המושגים: משתנה, ביטוי אלגברי, סדרה, איבר בסדרה, מקום בסדרה.
| סדרות בפיקסלים | תבנית בצורת O | סדרות ופונקציות |
 |
 |
מקור: desmos
אופי הפעילות: פעילויות אינטראקטיביות
תאור: פעילויות למציאת חוקיות והקשר לגרף. ניתן ליצור קוד עבור כיתה והתלמידים יכולים להגיש את הפתרונות.
הפעילויות: סדרות בפיקסלים, תבנית בצורת O וסדרות ופונקציות.

אופי הפעילות: פעילות חקר אינטראקטיבית
תאור: מאגר שיתופי של תבניות בתמונות. בתמונה שלושה- ארבעה צעדים ראשונים של הסדרה. ניתן לבקש מהתלמיד להשלים את המשך הסדרה, ולמצוא את החוקיות. אפשר גם לבקש מהתלמידים להמציא סדרה ולשלוח את התמונות לאתר.
 מקור: Dan Meyer
מקור: Dan Meyer
אופי הפעילות: סרטון, פעילות חקר
תאור: פעילות של דן מאייר "מתמטיקה בשלש מערכות". בסרטון נראה שדן בונה מקיסמים מבנה משולש. מה השאלה העולה בדעתך בהסתכלות בסרטון? במערכה השנייה מעלים את השאלות איזה מידע יש צורך בכדי לפתור את הבעיה? אילו כלים מתמטיים? ופותרים את הבעיה. הפעילות מלווה בסרטון.
 מקור: Dan Meyer
מקור: Dan Meyer
אופי הפעילות: סרטונים, פעילות חקר
תאור: פעילות של דן מאייר "מתמטיקה בשלש מערכות". בסרטון נראה מבנה של אבני דומינו הולכות וגדולות. מה יקרה אם נפיל את סדרת אבני הדומינו ? במערכה השנייה מעלים את השאלות איזה מידע יש צורך בכדי לפתור את הבעיה? אילו כלים מתמטיים? ופותרים את הבעיה. הפעילות מלווה בסרטונים.
ניתן לשלב את הבעיה במציאת חוקיות וכן בהכרות עם הפונקציה הלינארית.
 מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
אופי הפעילות: פיצוח - חקר בעזרת יישום דינאמי של NCTM
תאור: פיצוח ובו חקירה אינטראקטיבית של החוקיות של מספר הפגיעות הכדור בשולחן הביליארד.דרך משחק חוקרים מלבנים דומים, יחס הדמיון ומציאת המחלק המשותף הגדול ביותר, והמכפלה המשותפת הקטנה ביותר.
מומלץ גם לעיין במצגת "מפצחים את הדמיון" ודף פעילות מאת מיכל מלר בכנס המורים 2010.
 מקור: Nrich
מקור: Nrich
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: סימולטור למכונת פונקציות ריבועיות. יש להכניס מספר למכונה, לעקוב אחר תהליך החישוב שנערך בתוכה ולצפות בפלט. ניתן גם לשנות את החוקיות. כמו כן מוצג הקשר בין התבנית האלגברית לגרף הפרבולה באופן דינאמי. מלווה בסרטוני וידאו המסבירים את השימוש ובהדרכה למורה.
 מקור: Nrich
מקור: Nrich
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: סימולטור למכונת פונקציות לינאריות. יש להכניס מספר למכונה, לעקוב אחר תהליך החישוב שנערך בתוכה ולצפות בפלט. ניתן גם לשנות את החוקיות. כמו כן מוצג הקשר בין התבנית האלגברית לגרף הישר באופן דינאמי. מלווה בסרטוני וידאו המסבירים את השימוש ובהדרכה למורה.
 מקור: עמקים תבור
מקור: עמקים תבור
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: אוסף המלצות למשחקים אינטראקטיביים ברחבי הרשת העוסקים בחוקיות ובהמשכיות של סדרה. כמו כן ניתן למצוא גם שלושה מבדקים אינטראקטיביים בנושא חוקיות שחוברו על ידי מירטה לוין ונבנו על פי ספרי הלימוד. ההרשמה חינם.
 מקור: Visual Patterns
מקור: Visual Patterns
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: מורים ותלמידים מציעים תבניות חזותיות, תמונות של סדרת עצמים והאתגר למצוא את התבנית האלגברית המתארת את הסדרה. כל סדרה כזו מלווה בדף עבודה מנחה למציאת החוקיות.
 מקור: NGFL-cymru
מקור: NGFL-cymru
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: לוח מספרים אינטראקטיבי, בדומה ללוחות שנה. ניתן לחקור בו באופן פתוח, חוקיות של מספרים באופנים שונים, לגלות את התבנית האלגברית המתארת את החוקיות. וכן גם לגלות תבניות של הסכומים. ניתן לעצב את הלוח בדרכים שונות ולמצוא תבניות שונות של חוקיות. מתאים לראשית האלגברה.
 מקור: NGFL-cymru
מקור: NGFL-cymru
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: משחק אינטראקטיבי בו האתגר להעביר את הצפרדעים מצד לצד בדילוגים, לחפש את האסטרטגיה לנצחון ומעבר לכך להכליל ולמצוא את החוקיות של מספר הצעדים הדרושים להעביר n צפרדעים מעל m צפרדעים. הפעילות מלווה בהסברים ובהנחיות למורה.
 מקור: NGFL-cymru
מקור: NGFL-cymru
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: משחק אינטראקטיבי בו האתגר להעביר את פינגווין בלוח משבצות מצד לצד , כאשר יש משבצת חופשיה אחת . (בדומה למשחק סדור המספרים במשבצות 1-15) ניתן לשחק ברמות שונות , להקטין ולהגדיל את לוח המשבצות. האתגר לחפש את האסטרטגיה למספר צעדים מינימלי ומעבר לכך להכליל ולמצוא את החוקיות לכך בהתאם לגודל הלוח. הפעילות מלווה בהסברים ובהנחיות למורה.
 מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: הפיצוח עוסק בחוקיות, מציאת חוקים והכללות לתבניות גיאומטריות שונות כמבוא לאלגברה. הפיצוח מלווה ביישומים אינטראקטיביים שיסייעו בחקירה.
 מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: בפיצוח זה התלמידים יכירו את האגדה המפורסמת "גרגר האורז" (אגדת השחמט) העוסקת בהפתעה של השתנות של גידול פי שניים. התלמידים יבחנו את קצב הגידול וישוו זאת לגידול לינארי ואחר באמצעות טבלה וגרף דינאמיים.
 מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: פיצוח ובו תוך כדי התנסות מוחשית בבנייה בקוביות התלמידים יבחנו תהליכי השתנות באמצעות בניית טבלה וגרף דינאמיים.
 מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: הפיצוח עוסק בחקירת תהליכי גידול מעריכי. ניתן לשלב בלימוד חוקיות בכיתה ז או בהמשך בנושא סדרה הנדסית או בבעיות גדול ודעיכה. בפיצוח קישור לסרט "העבר את זה הלאה", סרטון אנימציה ממחיש את קצב הגידול ושאלות מנחות לחקירה בעזרת גליון אלקטרוני.
 מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: פיצוח העוסק בפיתוח הראיה המרחבית ומציאת חוקיות מעניינות תוך הסתכלות במשולשים שווי צלעות. הבעיות בפיצוח דורשות להסתכל בצורה הגיאומטרית השלמה ובחלקיה, למנות משולשים ולמצוא את החוקיות העומדת מאחורי המנייה ואף הכוונה להוכחת החוקיות באופן אלגברי. הבעיות מדורגות בקושי ומתאימות לתלמידים החל מכיתה ז'. (לגילאי 9-99). כולל סרטון.
 מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: פיצוח ובו חקירה אינטראקטיבית של החוקיות העומדת מאחורי משולש מספרים. פעילות זו מתאימה לשילוב בלימוד האלגברה החל מכיתות ז'.
תיאור: אוסף משימות העוסק בפתרון שאלות מילוליות המיועדות לתלמידי כיתה ז'. המשימות מדורגות בחלקן ומאפשרות שיח ופתרון אריתמטי (חשבוני) בהמשך למיומנויות שנלמדו בביה"ס היסודי, כך שכל תלמיד בכיתה ז' יוכל להתמודד עימן, גם אם טרם השיג שליטה במיומנויות האלגבריות הנדרשות לפתרון.
תיאור: בפעילות נזרעים זרעים לקראת פתרון בעיות ערך קיצון שנלמדות בכיתה ט' ובחטיבה העליונה.
תיאור: אוסף תרגילים בנושא הפונקציה הקווית, המיועד לחזרה על כל המושגים הקשורים בה, כגון: משמעות השיפוע ומדרגות, מצבים הדדיים בין ישרים, נקודות חיתוך עם הצירים, מציאת משוואת של ישרים. המשימות מקשרות גם ליישומונים מבהירים.
תיאור: פעילות זו עוסקת בקשר שבין שיפוע של פונקציה קווית, גובה המדרגה, רוחב המדרגה והיחס שבין הניצבים במשולש ישר זווית שבו היתר הוא חלק מהגרף של הפונקציה. מטרת הפעילות: זיהוי היחס הקבוע בין הניצבים בכל המשולשים שנבנים על אותו גרף. היחס הקבוע הוא המספר המייצג את השיפוע. הפעילות מדגישה את הקשר בין רוחב המדרגה, גובה המדרגה, היחס ביניהם והמספר המיצג את השיפוע. הפעילות אינה ממוקדת בטכניקה האלגברית המשרתת את מציאת השיפוע באמצעות מנת ההפרשים.
תיאור: פעילות זו עוסקת בהבנת הקשר בין קצב השינוי של הפונקציה לבין השיפוע של גרף הפונקציה דרך סיפור מחיי היום-יום – תהליך הורדה של תוכנה מהאינטרנט (בהנחה שקצב ההורדה קבוע). הפונקציות המוצגות בפעילות הן פונקציות יורדות המתארות את גודל התוכנה שנותר להורדה (ב-MB) כפונקציה של הזמן שחלף מתחילת ההורדה. פעילות זו היא פעילות המשך לפעילות: "שיפוע של פונקציה קווית – מותחים קפיצים", העוסקת במשמעות השיפוע בהקשר של סיפור, עבור פונקציות עולות.
תיאור: הפעילות עוסקת בהיבט האלגברי של מושג השיפוע של הפונקציה הקווית. מטרת הפעילות היא חיזוק המיומנות של השימוש במנת ההפרשים לחישוב השיפוע והבנת הקשר למושג: קצב שינוי. הפעילות מתחילה בבחינת השיפוע של פונקציה כלשהי ללא ביטוי מפורש. באופן זה מודגשת המשמעות של מנת ההפרשים.
תיאור: הפעילות נועדה לחזק את ההבנה של מושג השיפוע של פונקציה קווית דרך תיאור מקרה – סיפור. בסיפור: לקפיצים שונים מידת גמישות שונה. מידת הגמישות נלמדת באמצעות מדידות של אורכי הקפיצים בהתאם לכוח המופעל עליהם. כך ניתן לבנות גרפים על פי נקודות, בהן שיעור ה-X הוא מספר יחידות כוח שמופעלות על הקפיץ ושיעור ה-Y הוא אורך הקפיץ. מתוך המדידות השונות לומדים מהי מידת השינוי באורך הקפיץ בהפעלה של יחידת כוח אחת שהיא, למעשה, המספר המייצג את השיפוע.
מקור: MEI
תאור: משחקון אינטראקטיבי למחשב או לנייד בו על המסך רצות נקודות על הישר.
עליך להיות מהיר ולזהות איזה ישר מתואר בגרף. או לחלופין יהיה נתון ישר ושלושה גרפים ען נקודות נעות ועליך לבחור את הגרף הנכון.
המשחק הוא עם ניקוד ועל זמן.
בחרו מהתפריט את המשחקון: Straight Line Graphs
מקור: Desmos Teacher
תאור: משחקון אינטראקטיבי למחשב או לטאבלט בו צריך לתפוס כוכבים ע"י הפלת כדור. הכדור נופל וגולש על גבי גרפים של פונקציות קוויות אותם צריך התלמיד לבנות לפי מיקום הכוכבים.
הפעילות מתרגלת את משמעות השיפוע בשריג לפי יחס בין גובה מדרגה לרוחבה, ומייצרת תפיסה ויזואלית למספר החופשי בביטוי של הפונקציה הקווית לפי נקודת החיתוך המשוערת של הגרף הנבנה עם ציר ה- Y.
מקור: GeoGebra
תאור: פעילות עם יישומון שמדגימה בעיה של חקר פונקציות קוויות ומציאת נקודות חיתוך של ישרים.
היישומון מאפשר לשנות נתונים ולפתור בעיות רבות.
מחבר: Judah L Schwartz
 מקור:Desmos Teacher
מקור:Desmos Teacher
אופי הפעילות: שאלות אינטראקטיביות בדסמוס
תאור: אוסף פעילויות אינטראקטיביות מדורגות אך מאתגרות לבניית ישרים בייצוגיו השונים תוך שימוש בתוכנה Desmos. הפעילות במערכת Desmos Teacher, ניתן להגדיר כיתה ולעקוב אחר התקדמות התלמידים.
 מקור: Dan Meyer
מקור: Dan Meyer
אופי הפעילות: סרטונים, פעילות חקר
תאור: פעילות של דן מאייר "מתמטיקה בשלש מערכות". בסרטון נראה מבנה של אבני דומינו הולכות וגדולות. מה יקרה אם נפיל את סדרת אבני הדומינו ? במערכה השנייה מעלים את השאלות איזה מידע יש צורך בכדי לפתור את הבעיה? אילו כלים מתמטיים? ופותרים את הבעיה. הפעילות מלווה בסרטונים.
ניתן לשלב את הבעיה במציאת חוקיות וכן בהכרות עם הפונקציה הלינארית.
 מקור: PhET
מקור: PhET
אופי הפעילות: יישום דינאמי ואינטראקטיבי.
תיאור: חקירה של הקשר בין משוואת הישר ומשוואתו. התרגול מתנהל כמשחק.
 מקור: Khan academy
מקור: Khan academy
אופי הפעילות: תרגול אינטראקטיבי באקדמיית קאהן, מתורגם לעברית.
תיאור: בהינתן משוואת ישר, על התלמיד ליצור גרף ישר על ידי קביעת שתי נקודות עליו. התרגול מלווה בסרטון הסבר וברצף נושאי של משוואת הישר בסרטונים ובתרגול.
 מקור: Mangahigh
מקור: Mangahigh
אופי הפעילות: משחק אינטראקטיבי בו עשר רמות.
תיאור: לתרגול בניית משוואת הישר דרך שתי נקודות. המורה יכול לבנות כיתה ולעקוב אחר תוצאות התלמידים.
 מקור: nrich
מקור: nrich
אופי הפעילות: יישום דינאמי ובו סימולציה למכונת מספרים בה הקשר הוא לינארי.
תיאור: ניתן להכניס למכונה מספרים שונים, לצפות בתהליך החישוב ולנחש על פי התוצאות את הכלל לפיו עובדת המכונה. ביישום ניתן לחקור את הקשר לגרף הפונקציה ולטבלת המספרים. ניתן גם לבנות מכונות לפונקציות לינאריות שונות.
 מקור: nrich
מקור: nrich
אופי הפעילות: יישומים דינאמיים לחקירת המצב ההדדי של ישרים: ישרים מקבילים , ישרים מאונכים , שיקוף של ישרים לציר ה-x ולציר ה-y.
תיאור: ביישום ישרים מקבילים עליכם להזיז את הנקודות כך שיתקיים התנאי שהישרים יקבילו ולחקור את הקשר של הישרים במשוואות האלגבריות שלהם.
 מקור: nrich
מקור: nrich
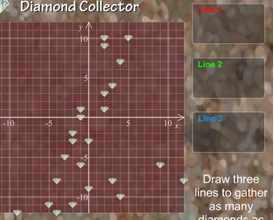
אופי הפעילות: משחק אינטראקטיבי מול המחשב או נגד חבר.
תיאור: האתגר הוא לחבר שלוש משוואות ישרים כך שיעברו דרך כמה שיותר נקודות בהן יהלומים.
 מקור: Fun Based Learning
מקור: Fun Based Learning
אופי הפעילות: משחק אינטראקטיבי לתרגול זיהוי ישרים ברמת מתחילים.
תיאור: יש להתאים משוואת ישר לנקודות נתונות במערכת הצירים. מטרתכם לאסוף כמה שיותר נקודות.
 מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
אופי הפעילות: יישום דינאמי לחקירת עליה וירידה של הישר.
תיאור: ביישום סימולציה של שני שטחים מלבניים, האחד מתמלא בצבע באופן קבוע והשני מתרוקן מצבע באופן קבוע. ניתן לעקוב אחר השתנות גובה הצבע בטבלאות המספריות, ובנקודות המתארות את גובה הצבע כפונקציה של הזמן. תוך האנימציה ניתן לראות בבירור את תהליך העליה והירידה ולחקור את הקשר לייצוג האלגברי.
 מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
אופי הפעילות: דף עבודה אינטראקטיבי בגאוגברה לחקירת השפעת הפרמטרים על משוואת הישר y=ax+b.
תיאור: כמו כן יש אפשרות לשרטט מדרגות שונות על פי שתי נקודות על הישר ולחקור את שיפוע הישר כיחס בין הפרש ה-y להפרש ה-x.
 מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
אופי הפעילות: דף עבודה ויישום דינאמי המבוססים על שאלה 21 בשאלון 801.
תיאור: ביישום מושם דגש על השיפועים השווים בגרף. יש אפשרות לשנות את השיפועים ולבדוק כיצד משתנה קצב גדילת השיער.
 מקור: אקדמיית קאהן בעברית
מקור: אקדמיית קאהן בעברית
אופי הפעילות: אוסף פעילויות של תרגול אינטראקטיבי, לתרגול פתרון אי שוויונות קוויים, המלוות בסרטונים של שיעורים מתורגמים באוניברסיטת קאהן. בכל תרגול התלמיד יכול לצבור נקודות והמורה יכול לצפות בהישגיו:
2. תרגול שרטוט אי שוויון קווי וזיהוי נקודות שהן פתרונם.
3. שרטוט מערכת אי שוויונות קוויים
4. שרטוט מערכת אי שוויונות קוויים וזיהוי נקודות שהן פתרונם.
 מקור: interacivate , NSDL
מקור: interacivate , NSDL
אופי הפעילות: שיעור הכולל הסברים, דפי עבודה וכלי דינאמי לפתרון אי שוויונות קוויים באופן גרפי.
 מקור: הילקוט הדיגיטלי- אופק על יסודי של מט"ח
מקור: הילקוט הדיגיטלי- אופק על יסודי של מט"ח
אופי הפעילות: בפעילות נתון סרטוט שבו מוצג פתרון של אי־שוויון בין שתי פונקציות, ויש לרשום אי־שוויון בין פונקציות שהפתרון מתאים לו. מומלץ להשתמש בכלים דינאמיים (של מטח או אחר כגון גאוגברה).
 מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
אופי הפעילות: הפיצוח עוסק בבעיות מתמטיות מילוליות בנושא הישר העשויות לעורר דיון בערכים חברתיים כגון עזרה הדדית, חברות, חסכון ועוד.
הבעיות עוסקות במשוואת הישר, באי שוויונות בין ישרים ומציאת נקודות חיתוך בין ישרים, בשילוב יישומים דינאמיים.
הפעילויות פותחו ועובדו על פי - שילוב החינוך לערכים בהוראת המתמטיקה, ד"ר יעל אדרי ("שער-חם", 2008)
תודות ליעל על תרומתה ושיתוף הפעולה.
 מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
אופי הפעילות: הפיצוח שלפניכם עוסק בהתרת אי שוויון לינארי בעזרת גרף והוא החלק הראשון בנושא. הפיצוח הבא יעסוק במערכת אי שוויונים לינאריים.
בפיצוח אוסף שאלות, העוסקות בבעיות מחיי היום יום, ומיועדות להצגת הנושא ותרגולו לתלמידי כיתות ח-ט.
מצורפים גם קישורים ליישומים אינטראקטיביים לפתרון אי שיוויונות בעזרת גרפים ודפי עבודה לתלמיד בנושא.
 מקור: שאלות לדוגמה ממבחני פיזה. בתרגום: ראמ"ה
מקור: שאלות לדוגמה ממבחני פיזה. בתרגום: ראמ"ה
 מקור: מטח
מקור: מטח מקור: flashymaths
מקור: flashymaths
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: תרגול אינטראקטיבי לפתרון משוואות פשוטות ממעלה ראשונה. בכל שלב באפשרותך לבחור איזו פעולה יש להפעיל על כל אחד מאגפי המשוואה ולצפות באופן דינאמי וממחיש בתוצאה. התהליך ממשיך עד לפתרון המשוואה.
להפעלה אנא הסירו חסימת Flash מדריך הסרת Flash
 מקור: National Library of Virtual Manipulatives
מקור: National Library of Virtual Manipulatives
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: יישום אינטראקטיבי לפתרון משוואות במודל המלבנים.

מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: בפעילות מוצגים טריקים שונים לכפל מספרים בעזרת האצבעות שמהן יוכלו ליהנות תלמידים צעירים והבוגרים שביניהם יוכלו גם לחקור מהו הקסם המתמטי העומד מאחורי טריקים אלו. בפעילות זו אתם מתבקשים לצפות בסרטים המציגים את הטריקים, להוכיח באופן אלגברי (או אחר) מדוע השיטות הללו עובדות, להרחיב ולהכליל אותן. ניתן לשלב פעילויות אלו בפרק של בעיות מספרים.

מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: פתרון משוואות לינאריות פשוטות בעזרת המחשה ויזואלית וידידותית. נפתור משוואות בעזרת שימוש במודל המלבנים, שהכרנו בפיצוח "בארץ יצורי הפרא המתמטיים" להצגת מספרים שליליים. הפיצוח כולל סרטוני וידאו המציגים את המודל, יישומון דינאמי וכן דפי עבודה עצמית לתלמיד. ניתן לשלב בשימוש הלוח החכם.
תיאור: בפעילות זו מתבקשים התלמידים לענות על השאלה כמה פתרונות יש למערכת של שתי משוואות בשני משתנים ללא מציאת הפתרונות עצמם. בחלק מהשאלות נתונות מערכות של שתי משוואות ממעלה ראשונה, באחרות מערכות של משוואה ממעלה ראשונה ומשוואה ממעלה שנייה ובחלק אחר שתי משוואות ממעלה שנייה.
 מקור: Desmos Teacher
מקור: Desmos Teacher
אופי הפעילות: שאלות אינטראקטיביות בדסמוס
תאור: פעילות חקר אינטראקטיבית להבנת פתרון מערכת משוואות לינאריות באופן גרפי תוך שימוש בתוכנה Desmos.
מקור: GeoGebra
תאור: פעילות עם יישומון שמדגימה פתרון בעיה שדורשת שתי משוואות לינאריות בשני נעלמים באמצעות חיתוך של שני ישרים.
היישומון מאפשר לשנות נתונים ולפתור בעיות רבות.
מחבר: Judah L Schwartz
 מקור: עבודת סיכום של עמרי נווה קורס סרטונים במתמטיקה.
מקור: עבודת סיכום של עמרי נווה קורס סרטונים במתמטיקה.
אופי הפעילות: סרטון המבוסס מצגת prezi.
תיאור: מוצגת בעיה מהחיים שפתרונה הוא במערכת שתי משוואות ממעלה ראשונה. במהלך הסרטון מוצגות דרכים שונות לפתרון ונערך דיון על משמעות הפתרון.
לפניכם יחידת לימוד העוסקת בקריאת גרפים ומיועדת לתלמידי כיתות ח' ו-ט'. המשימות עוסקות בנושאים שונים, בחלקן מכילות יישומונים.
להלן סדר הפעילויות המתאים לעבודה באמצעות היחידה:
- טבלה וגרף
- מצגת: טבלה וגרף / بالعربية
- טבלה וגרף - הכנסה כספית - גרף משולב מכמה קטעי גרפים
- מצגת: גרף משולב מכמה מקטעי גרפים - צריכת סוכר / بالعربية
- גרף משולב מכמה מקטעי גרפים - השוואה בין גרפים
- מצגת: השוואה בין גרפים - נשים וגברים באקדמיה / بالعربية
- השוואה בין גרפים – משימה: מרחק מכדור הארץ - משימות מסכמות - גרף משולג והשוואה בין גרפים
- משימה מסכמת 1 – גרף משולב והשוואה בין גרפים – ממוצע ציונים
- משימה מסכמת 2 – גרף משולב והשוואה בין גרפים – אימון ריצה
תיאור: הפעילות מתאימה לתלמידי כיתה ז' ו-ח' בקבוצות הגבוהות. במהלך פתרונה התלמידים מתמודדים עם פענוח מידע ופירוש של נתונים ונדרשים להמרות בין ייצוגים, תוך שימוש בשיקולים ובמיומנויות המתמטיות הבאות: חיבור וחיסור מספרים מכוונים, ערך מוחלט של מספר מכוון, הבנה של המושג 'מרחק נקודה מישר' וההבדל בינו לבין מרחק בין שתי נקודות, קריאת נתונים מתוך גרף, זיהוי המשמעות של הנתונים, בניית גרף, חשיבה והנמקה.
תיאור: בפעילות נזרעים זרעים לקראת פתרון בעיות ערך קיצון שנלמדות בכיתה ט' ובחטיבה העליונה.
תיאור: המשימה היא משימה אוריינית הדורשת קריאה ופענוח נתונים מתוך פיסקת מידע ויכולה להתאים לתלמידים ברמות הגבוהות בכיתות ח.
תיאור: המשימות בפעילות משלבות בין התחום האלגברי והתחום הגיאומטרי. בתחום האלגברי נדרשות מיומנויות הקשורות לתכונות הפונקציה הקווית ובתחום הגיאומטרי המשימות עוסקות בחפיפת משולשים, דמיון משולשים ותכונות של משולשים שווי שוקיים. השאלות מדורגות כך שבמעבר בין סעיפים יש עליה בדרגת החשיבה הנדרשת לצורך הפתרון. המשימות מתאימות לתלמידי כיתות ח' ברמות הגבוהות אך ניתן לעשות בהן שימוש גם בכיתה ט' כחזרה וריענון על הפרקים שנלמדו בכיתה ח'.
תיאור: הפעילות עוסקת בפונקציות קוויות וצורות גאומטריות שיוצרים הגרפים שלהן במערכת צירים. במסגרת ההוראה של הנושא 'פונקציה קווית' עוסקים בתכונות של הגרפים, כמו מקבילות או חיתוך בין ישרים. בהוראת התחום הגאומטרי עוסקים בחפיפת משולשים, דמיון משולשים, תכונות ומשפטים הקשורים במשולשים שווי שוקיים או משולשים ישרי זווית. השילוב בין התחומים מוצע בפעילות זו באמצעות קישור בין תכונות היסוד של מערכת צירים מאונכת, לבין תכונות גיאומטריות של מרובעים ומשולשים. התלמידים נדרשים להתייחס לתכונות של גרפים, לאפיין באמצעותם מרובעים ומשולשים, למצוא נקודות חיתוך של ישרים, ולחשב אורכים, יחס בין אורכים, שטחים והיקפים. בפעילות נדרש גם שימוש במשפט פיתגורס.
תיאור: הפעילות עוסקת בפתרון שאלות תנועה בדרך גרפית תוך שילוב בין הנושאים: פונקציה קווית, יחס, חפיפת משולשים ודמיון משולשים. הפעילות עוסקת בגרפים המתארים מרחק מנקודת יציאה כפונקציה של זמן. בגרפים אלה משמעות השיפוע היא מהירות. כשמדובר בשני גרפים במערכת צירים אחת מבחינים בין מקרים בהם מתוארת יציאה מאותו מקום בהפרש זמנים או יציאה ממקומות שונים באותו זמן או בהפרש זמנים. הפתרונות הנדרשים מבוססים על הבנה ולא על טכניקה אלגברית.
תיאור: אוסף משימות קצרות שמטרתן לחדד, להעמיק את ההבנה ולעורר שיח מתמטי בכיתה. המשימות מתאימות לתלמידי כיתה ט' ברמות הגבוהות. השאלות עוסקות בטכניקה אלגברית הקשורה לביטויים ריבועיים ולפונקציות ריבועיות ולייצוג הגרפי שלהן כפרבולות.
תיאור: מטרת הפעילות היא לתרגל פירוק לגורמים לפי: זיהוי גורם משותף ונוסחאות כפל מקוצר. הפירוק ישמש לחישובים מהירים וקלים, הוכחת התחלקויות ופתרון בעיות.
תיאור: מטרת הפעילות היא לחזק אצל התלמידים את המיומנות האלגברית בנושא פירוק לגורמים, ולהשתמש בפירוק לצמצום שברים אלגבריים ולפתרון משוואות בדרך קלה. התרגול כולל שימוש בכל ארבע השיטות של פירוק לגורמים: הוצאת גורם משותף, פירוק בעזרת נוסחאות הכפל המקוצר, פירוק לפי קבוצות, פירוק הטרינום.
 מקור: Wolfram demonstration
מקור: Wolfram demonstration
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: המחשה דינאמית של הנוסחה המקוצרת של העלאה בחזקת שלש סכום חד איברים ויצירת נפח תיבה.
 מקור: NGFL-cymru
מקור: NGFL-cymru
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: הצגה דינאמית בפלאש של פירוק הביטוי a+b)n) בעזרת משולש פסקל.
מקור: אתר הפייסבוק של עידן טל
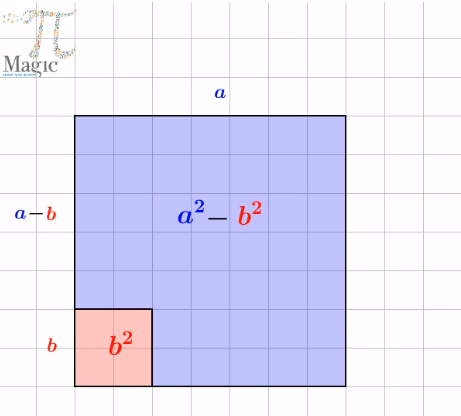
אופי הפעילות: תמונה דינאמית ממחישה ומעוררת דיון כיתתי
תיאור: התמונה הדינאמית מציגה משמעות גיאומטרית לנוסחה: (a^2-b^2=(a+b) (a-b
 מקור: Wolfram demonstration
מקור: Wolfram demonstration
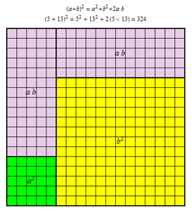
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור:המחשה דינאמית של הנוסחה המקוצרת של ריבוע סכום חד איברים.
 מקור: youtube
מקור: youtube
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: סדרת סרטונים בעברית ובהם הדגמה להוכחות ויזואליות בעזרת פאזל של נוסחאות הכפל המקוצר.
 מקור: שיעורטון
מקור: שיעורטון
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: שיעור מוסרט ובו פיתוח והמחשה של נוסחאות הכפל המקוצר.
 מקור: illuminations
מקור: illuminations
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: הדגמה ויזואלית וחקירה של נוסחת ריבוע הסכום. a+b)2).
 מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: הפיצוח "הפרש ריבועים", כשמו כן הוא, עוסק בנוסחת הפרש ריבועים כולל הוכחות אינטראקטיביות ללא מילים, חידות ושאלות חקר הדורשות יישום הנוסחה ואפילו הוכחת משפט מתמטי, הידוע כמשפטון פרמה.
תיאור: פעילות זו עוסקת במיומנות האלגברית של השלמה לריבוע. מיומנות זו תהיה חיונית לתלמידים בעת המעבר מההצגה הכללית של פונקציה ריבועית להצגה הקדקודית, וכן לביסוס השיטה לפתרון משוואות ממעלה שנייה. בהמשך, בחטיבה העליונה היא תידרש לצורך רישום משוואת מעגל בצורה מפורשת, המאפשרת לזהות את רדיוס המעגל ואת מרכזו.
מבט גיאומטרי על התהליך נותן פירוש נוסף לתהליך האלגברי, ולתלמידים רבים הוא מספק מודל המאפשר לזכור או לשחזר את התהליך בכל עת. המודל מלווה ביישומון.
 מקור: Michigan virtual university
מקור: Michigan virtual university
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: תרגול אינטראקטיבי בו יש לבנות לביטוי האלגברי שטח ריבועי בעזרת בדידים (מודל המלבנים). יש לבנות את הפאזל ולצידו לשים את המלבנים המתאימים, כך שיתקבל הביטוי האלגברי המתאים.
 מקור:Malinc.se
מקור:Malinc.se
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור:יישום דינאמי בו המחשה לפירוק x^2 +bx והשלמתו לריבוע. יש אפשרות להזיז ולסובב את חלקי הפאזל עד להשלמת הריבוע ולפות במשמעות האלברית. כמו כן חקירה של הפונקציה הריבועית בצורה הקודקודית.
 מקור: Geogebra wiki
מקור: Geogebra wiki
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: יישום דינאמי להשלמה של ביטויים אלגבריים לריבוע בהיבט של האלגברה, השטחים והפונקציה.
 מקור: illumination
מקור: illumination
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור:הוכחה ללא מילים ודינאמית לתהליך השלמה לריבוע לשם פתרון משוואות ריבועיות.
מדוע x2 + ax = (x + a/2)2 – (a/2)2 ?
תיאור: מטרת הפעילות היא לחזק אצל התלמידים את המיומנות האלגברית בנושא פירוק לגורמים, ולהשתמש בפירוק לצמצום שברים אלגבריים ולפתרון משוואות בדרך קלה. התרגול כולל שימוש בכל ארבע השיטות של פירוק לגורמים: הוצאת גורם משותף, פירוק בעזרת נוסחאות הכפל המקוצר, פירוק לפי קבוצות, פירוק הטרינום.
 מקור: Michigan virtual university
מקור: Michigan virtual university
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור:תרגול אינטראקטיבי בו יש לבנות לביטוי האלגברי שטח מלבני בעזרת בדידים (מודל המלבנים). בעזרת מודל זה ניתן לפתור משוואות, לפרק טרינום, להשלים טרינום לריבוע ועוד תוך המחשה ויזואלית של הביטויים האלגבריים והפעולות עליהם. פעילות דומה בפיצוח יצורי הפרא לומדים לפתור משוואות .
 מקור: Hwb
מקור: Hwb
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: יישום דינאמי ואינטראקטיבי , מתאים לשימוש בלוח חכם. לאחר מתן התשובה מוצג סרטון המדגים את כפל רב איבר ובדיקת התשובה. ניתן להגריל תרגיל, או ליצור תרגיל משלך.
 מקור: Hwb
מקור: Hwb
אופי הפעילות: תרגול פירוק טרינום
תאור: יישום דינאמי ואינטראקטיבי העוסק בפירוק הטרינום למכפלה של שני גורמים, ברמות קושי שונות. מאפשר תרגול עם משוב.
הערה: בחרו באפשרות Quiz כדי להגיע לפעילות.
תיאור: אוסף משימות קצרות שמטרתן לחדד, להעמיק את ההבנה ולעורר שיח מתמטי בכיתה. המשימות מתאימות לתלמידי כיתה ט' ברמות הגבוהות. השאלות עוסקות בטכניקה אלגברית הקשורה לביטויים ריבועיים ולפונקציות ריבועיות ולייצוג הגרפי שלהן כפרבולות.
תיאור: אוסף משימות העוסק בייצוגים שונים של פונקציה ריבועית ובמעבר ביניהם. המשימות הן משימות קצרות שמטרתן לחדד, להעמיק את ההבנה ולעורר שיח מתמטי בכיתה. המשימות מתאימות לתלמידי כיתה ט' ברמות הגבוהות.
תיאור: הפעילות עוסקת בקשר שבין ההצגה הגרפית של הפונקציה הריבועית לבין משוואות שניתן לפתור תוך התבוננות בגרף. מתאימה לשילוב לאחר ההכרות עם הצורה הקודקודית ועם הצורה הכללית של פונקציה ריבועית, אך טרם הצגת הדרכים האלגבריות לפתרון משוואה ריבועית. הדיון הוא במספר פתרונות, או בפתרונות שניתן להסיק מהצגה גרפית נתונה ומתכונות הפרבולה.
תיאור: הפעילות עוסקת במעבר בין הייצוג הגרפי של הפונקציה הריבועית, לבין שלושת הייצוגים האלגבריים שלה: הצורה הקודקודית, הצורה הכפלית והצורה הכללית. חקר התכונות של הפונקציה הריבועית בפעילות זו, מתבצע על ידי מעבר בין הייצוגים השונים, כמעט מבלי לבצע חישובים.
תיאור: פעילות זו עוסקת במשפחות של פונקציות. הדגש בפעילות זו הוא ההיבט הגרפי. התלמידים מכירים משפחות של פונקציות ריבועיות מהצורות הבאות:
f(x)=〖ax〗^2 ; f(x)=〖ax〗^2+c ; f(x)=〖a(x-p)〗^2 ; f(x)=〖a(x-p)〗^2+k
בפעילות זו נדון במשפחות אחרות של פונקציות – משפחות שבכל אחת מהן לכל הפונקציות השייכות למשפחה יש נקודה משותפת – מעין "נעץ".
המטרה בפעילות זו היא שהתלמידים יאפיינו כל אחת מהמשפחות של הפונקציות, יבחינו בתכונות המשותפות לפונקציות השייכות למשפחה ויחקרו את תכונות המשפחה וכך יבינו את תפקיד הפרמטר בכל אחת מהמשפחות.
בפעילות התלמידים מתבקשים לזהות את הדמיון ואת השוני בין הפונקציות השייכות לאותה משפחה, למיין גרפים וביטויים השייכים או לא שייכים למשפחה ולקבוע את ערך הפרמטר לפי נתונים אודות פונקציה מסוימת השייכת למשפחה.
מומלץ לבצע אחרי פעילות זו את פעילות ההמשך "פונקציה ריבועית בקשר משפחתי – חלק ב'" שבה יש צורך להפעלה של טכניקה אלגברית.
תיאור: פעילות זו היא פעילות המשך לפעילות שעסקה במשפחות של פונקציות. בפעילות הראשונה הודגש ההיבט הגרפי, והופיעו בה משפחות של פונקציות שבכל אחת מהן לכל הפונקציות הייתה נקודה משותפת. בפעילות זו הדגש אלגברי והאפיון אינו בהכרח נקודה משותפת. הפעילות מזמנת צורך להפעלה של טכניקה אלגברית: הצבת ערך מספרי בביטוי אלגברי, פתרון משוואות ריבועיות ולינאריות, פתרון אי-שוויונות, שימוש בנוסחאות הכפל המקוצר, פעולות בביטויים אלגבריים, פתרון משוואה ריבועית פשוטה עם פרמטר והתייחסות לשיעור ה-x של קדקוד הפרבולה.
מומלץ לבצע את הפעילות כהמשך לפעילות "פונקציה ריבועית בקשר משפחתי – חלק א".

מקור: אתר הפייסבוק של עידן טל
אופי הפעילות: תמונה דינאמית ממחישה ומעוררת דיון כיתתי
תיאור: התמונה מציגה הזזות של הפרבולה המתאימה לפונקציה y=x^2 אל מול השינוי ביצוגים האלגבריים.
 מקור: Dan Meyer
מקור: Dan Meyer
אופי הפעילות: סרטון, פעילות חקר
תאור: פעילות של דן מאייר "מתמטיקה בשלש מערכות". בסרטון נראה שדן בונה מקיסמים מבנה משולש. מה השאלה העולה בדעתך בהסתכלות בסרטון? במערכה השנייה מעלים את השאלות איזה מידע יש צורך בכדי לפתור את הבעיה? אילו כלים מתמטיים? ופותרים את הבעיה. הפעילות מלווה בסרטון.
 מקור: Dan Meyer
מקור: Dan Meyer
אופי הפעילות: סרטון וחקר בעזרת יישום דינאמי
תאור: פעילות של דן מאייר "מתמטיקה בשלש מערכות". מה השאלה העולה בדעתך בהסתכלות בתמונה או בסרטון? במערכה השניה מעלים את השאלות איזה מידע יש צורך בכדי לפתור את הבעיה? אילו כלים מתמטיים? ופותרים את הבעיה. הפעילות מלווה בסרטונים וביישום דינאמי.
במערכה האחרונה סרטון המציג את הפתרון.
הבעיה מופיעה גם בתוכנית המוארת של משימות אוריינות
 מקור: The Future Channel
מקור: The Future Channel
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: סרטון קצר – גלישת גלים המציג את תהליך בניית גלשן הגלים וכיצד נעזרים במתמטיקה ובידע על הפרבולה לתכנונו. מצורף גם דף עבודה (אנגלית).
 מקור: Get the Math
מקור: Get the Math
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: Math in Basketball מתמטיקה במשחק הכדורסל - פעילות אינטראקטיבית מלווה בסרט וידאו המסביר כיצד ניתן לתכנן את הקליעה המושלמת לסל בעזרת המתמטיקה.
 מקור:(Illuminations (NCTM
מקור:(Illuminations (NCTM
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: מאזני משוואות: יישום אינטראקטיבי לפתרון משוואות ריבועיות בייצוג גרפי ובייצוג מספרי על מאזניים בהם "שוקלים" הצבה מספרים בשני אגפי המשוואה.
 מקור: MathWareHouse
מקור: MathWareHouse
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: פרבולה אינטראקטיבית , יישום אינטראקטיבי לחקירת הפרמטרים במשוואה הריבועית הסטנדרטית וכן בצורה הקודקודית.
 מקור: מט"ח
מקור: מט"ח
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: ספר אלקטרוני בו אוסף פעילויות אינטראקטיביות בנושא הפונקציה הריבועית בייצוגיה השונים, העתקות ויישומים בחיים. הפעילויות מלוות בבעיות חקר, ובתרגול אינטראקטיבי.
 מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: פיצוח - פעילויות מגוונות ובלתי שגרתיות בנושא הפרבולה. הפעילות יכולה לשמש כהעשרה או כתרגול מרענן בסוף הוראת הנושא. מצורפים גם קישורים לפעילויות ומאמרים בנושא.
 מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
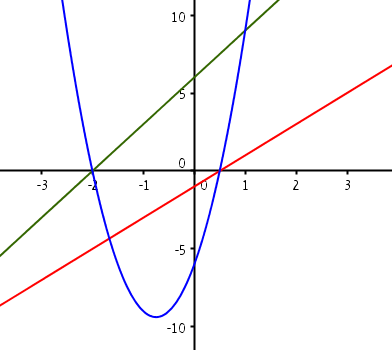
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: יישום אינטראקטיבי לפעילות חקר של בניית הפונקציה הריבועית לפי מכפלה של שני ישרים. מתבסס על המאמר: "נחיתה רכה של הפונקציה הריבועית" מאת פרופ נצה מובשוביץ הדר. ועל האוגדן למדריך.
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: יישומונים לחקירת תפקיד הקודקוד על פי שאלות מתוך שאלון 802.
 מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: יישומון תרגול למציאת הקודקוד –מירטה.
 מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: דף עבודה ויישום דינאמי לחקירת גרף הפונקציה הריבועית המוצגת בצורה המוזזת.
 מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: דף עבודה ויישום דינאמי לחקירת גרף הפונקציה הריבועית המוצגת בצורה המוזזת.
 נושא: הפונקציה הריבועית בייצוגים שונים.
נושא: הפונקציה הריבועית בייצוגים שונים.
כיתה: ט
תיאור: הישומון מופיע בפעילות: למצוא את הפתרון הטוב ביותר – חלק א העוסקת בבעיות ערך קיצון, אותן ניתן לפתור באמצעות מציאת קודקוד של פרבולה. בישומון ניתן לעקוב אחר השינוי בשטח הרצפה בצמוד לשינוי בגרף הפונקציה המתארת אותו.
 נושא: הפונקציה הריבועית בייצוגים שונים.
נושא: הפונקציה הריבועית בייצוגים שונים.
כיתה: ט
תיאור:
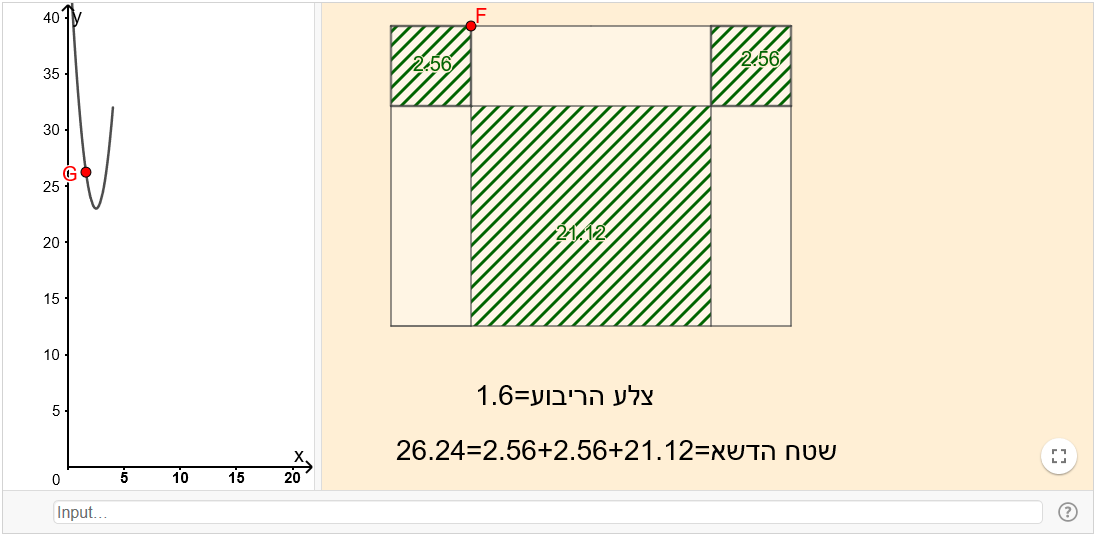
תיאור: היישומון מופיע בפעילות: למצוא את הפתרון הטוב ביותר – חלק א העוסקת בבעיות ערך קיצון, אותן ניתן לפתור באמצעות מציאת קודקוד של פרבולה. הישומון מתאים לבעיה העוסקת בשטח של גינה. ניתן לעקוב אחר שינוי בשטח הגינה בצמוד לשינוי בגרף הפונקציה המתארת אותו.
 נושא: הפונקציה הריבועית בייצוגים שונים.
נושא: הפונקציה הריבועית בייצוגים שונים.
כיתה: ט
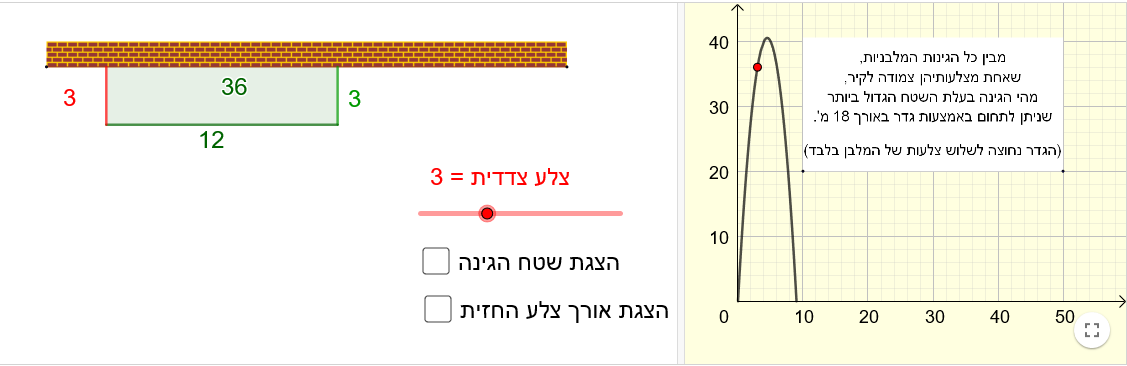
תיאור: היישומון מופיע בפעילות: למצוא את הפתרון הטוב ביתר – חלק ב . פעילות זו עוסקת במציאת מלבן בעל שטח גדול ביותר. היישומון מאפשר לעקוב אחר השתנות שטח הגינה כאשר משנים את צלעותיה.
 נושא: הפונקציה ריבועית בייצוגים שונים
נושא: הפונקציה ריבועית בייצוגים שונים
כיתה: ט
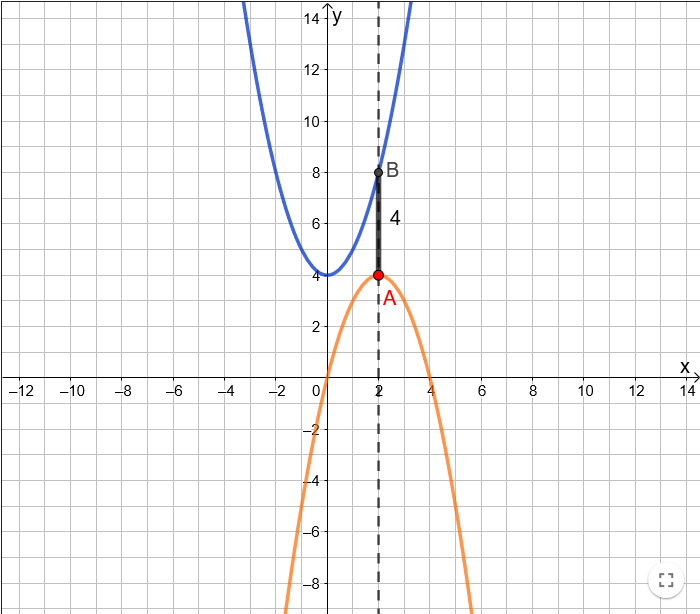
תיאור: היישומון מופיע בפעילות: למצוא את הפתרון הטוב ביותר – חלק ג. פעילות זו עוסקת בבעיות ערך קיצון, אותן ניתן לפתור באמצעות מציאת קודקוד של פרבולה. היישומון מראה את השתנות אורך קטע בין שתי נקודות על שתי פרבולות, כאשר גוררים את אחת הנקודות.
תיאור: פעילות זו היא חלק ממקבץ של שלוש פעילויות שעוסקות בבעיות ערך קיצון, אותן ניתן לפתור באמצעות מציאת קודקוד של פרבולה. בחטיבה העליונה התלמידים יעסקו בפתרון בעיות ערך קיצון מסוגים שונים, וירכשו כלים נוספים למצוא את הפתרון הטוב ביותר.
הפעילויות בנויות באופן שמאפשר עיסוק בפונקציות ממעלה שנייה בהקשר מציאותי, הבנה של מהות הבעייה לפני שלב הפתרון הטכני, הצמחת הרעיון של חיפוש המינימום או המקסימום באמצעות קודקוד של פרבולה, המחשת החשיבות של תחום ההגדרה של הפונקציה המתאים לבעיה.
ברוב הבעיות משולבים יישומונים שממחישים את הדינמיות של הבעיות, ומאפשרים לתלמידים לחקור ולהעלות השערות לפני פתרון בכלים אלגבריים.
בפעילות זו שתי בעיות: בעיה בה מחפשים את המלבן בעל השטח הגדול ביותר, מבין כל המלבנים בעלי היקף נתון. ובעיה בה מתכננים גינה המורכבת ממדשאות וערוגות פרחים בשטח מלבני נתון. גם פעילות זו מלווה ביישומון.
תיאור: פעילות זו היא חלק ממקבץ של שלוש פעילויות שעוסקות בבעיות ערך קיצון, אותן ניתן לפתור באמצעות מציאת קודקוד של פרבולה. בחטיבה העליונה התלמידים יעסקו בפתרון בעיות ערך קיצון מסוגים שונים, וירכשו כלים נוספים למצוא את הפתרון הטוב ביותר.
הפעילויות בנויות באופן שמאפשר עיסוק בפונקציות ממעלה שנייה בהקשר מציאותי, הבנה של מהות הבעייה לפני שלב הפתרון הטכני, הצמחת הרעיון של חיפוש המינימום או המקסימום באמצעות קודקוד של פרבולה, המחשת החשיבות של תחום ההגדרה של הפונקציה המתאים לבעיה.
ברוב הבעיות משולבים יישומונים שממחישים את הדינמיות של הבעיות, ומאפשרים לתלמידים לחקור ולהעלות השערות לפני פתרון בכלים אלגבריים.
בפעילות זו מוצגת בעיה שעוסקת במציאת מלבן בעל שטח גדול ביותר, כאשר נתון סכום האורכים של שלוש מצלעות המלבן, ולא היקפו, ולכן, בשונה מבעיה קודמת ומצפיות התלמידים, הפתרון הטוב ביותר מתקבל עבור מלבן שאינו ריבוע.
תיאור: פעילות זו היא חלק ממקבץ של שלוש פעילויות שעוסקות בבעיות ערך קיצון, אותן ניתן לפתור באמצעות מציאת קודקוד של פרבולה. בחטיבה העליונה התלמידים יעסקו בפתרון בעיות ערך קיצון מסוגים שונים, וירכשו כלים נוספים למצוא את הפתרון הטוב ביותר.
הפעילויות בנויות באופן שמאפשר עיסוק בפונקציות ממעלה שנייה בהקשר מציאותי, הבנה של מהות הבעייה לפני שלב הפתרון הטכני, הצמחת הרעיון של חיפוש המינימום או המקסימום באמצעות קודקוד של פרבולה, המחשת החשיבות של תחום ההגדרה של הפונקציה המתאים לבעיה.
ברוב הבעיות משולבים יישומונים שממחישים את הדינמיות של הבעיות, ומאפשרים לתלמידים לחקור ולהעלות השערות לפני פתרון בכלים אלגבריים.
הבעיות: 'מופע בפארק', 'זוגות מספרים' ו'בין שתי פרבולות' מגוונות את התכנים בהן מטפלות בעיות ערך קיצון – הן לא עוסקות במלבנים וריבועים כפי שהוצג בשני החלקים הקודמים.
תיאור: הפעילויות שלפנינו נוגעות במושג היחס.
מטרות הפעילויות הן:
- להדגיש את כוחה של האלגברה ככלי להוכחה.
- לתרגל שימוש בשברים אלגבריים בתוך הקשר שבו ניתן לייחס משמעות לתוצאות של המניפולציות האלגבריות.
- לעודד שיקולים הקשורים ליחסים בין גדלים נתונים, שלעתים יכולים להחליף פתרון משוואות, או לאפשר, אמצעות שיקולים כאלה, בקרה על פתרונות שהתקבלו באופן אלגברי.
- להצביע על דמיון בין בעיות דרך ובעיות הספק.
- למורה
- לתלמיד / بالعربية
 מקור: המרכז הארצי למורים למתמטיקה
מקור: המרכז הארצי למורים למתמטיקה
אופי הפעילות: יישומון
תאור: מתבסס על שאלה מתוך דוגמאות למבחני פיזה 2012. היישומון מדמה דלת מסתובבת עם שלש כנפיים. ניתן לשנות את מספר הכנפיים בדלת וכן את מימדי הפתחים.
 מקור: המרכז הארצי למורים למתמטיקה
מקור: המרכז הארצי למורים למתמטיקה
אופי הפעילות: יישומון
תאור: מתבסס על שאלה מתוך משימות האוריינות לכיתה ט בגלגל הענק בנושא שאלות מילוליות.
המשימה אינטגרטיבית ומשלבת נושאים שונים כגון: היקף מעגל ומקטע, גיאומטריה של משולשים ומרובעים, סימטריה במעגל ועוד.
היישומון מדמה את סיבובי גלגל הענק ושני רוכבים עליו. ניתן לשנות את מימדי הגלגל ואת מספר המושבים בו.
אופי הפעילות: מצגת ויישומים דינאמיים.
תיאור: מצגת המציעה פעילות המלווה את המשימה האוריינית "האופניים" ממבחני הפיזה. בבעיה שני חלקים: האחד עוסק במרחק הנסיעה של גלגלי האופניים בליווי היישומון גלגלי האופניים.
החלק השני עוסק בפעולת ההילוכים של האופניים וחקר בנושא היחס בליווי היישומון אופניים עם הילוכים.
היישומונים בהפקת אלנט עבור אגף טכנולוגיות מידע במשרד החינוך.
 מקור: שאלות לדוגמה ממבחני פיזה בתרגום: ראמ"ה
מקור: שאלות לדוגמה ממבחני פיזה בתרגום: ראמ"ה
אופי הפעילות: מצגת ויישום דינאמי.
תיאור: מצגת המציעה פעילות שאילת שאלות סביב הסיטואציה של מכירת עיתונים המוצגת בבעיהבהפקת אלנט עבור אגף טכנולוגיות מידע במשרד החינוך.
 מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
אופי הפעילות: משימה אוריינית מלווה בסרטון ויישום דינאמי
תיאור: משימה אוריינית ובה בעיה מילולית מן המציאות המובילה לפתרון משוואות. היישום הדינאמי מציג בצורה מוחשית את המתואר בבעיה ומאפשר חקירתה ואף הרחבתה.
הפעילות מלווה בדף עבודה, יישום דינאמי 1, יישום דינאמי 2.
המשימה "שומר מסך" מופיעה גם במשימות אוריינות כולל דף עבודה ופתרונו.
 מקור: משרד החינוך, המזכירות הפדגוגית, תכנון ופיתוח תכניות לימודים ומכון ויצמן
מקור: משרד החינוך, המזכירות הפדגוגית, תכנון ופיתוח תכניות לימודים ומכון ויצמן
אופי הפעילות: משימה אוריינית מלווה בסרטון אינטראקטיביי
תאור: האיכר שתל במטע ריבועי עצי תפוחים וכדי להגן על העצים נטע מסביבו עצי ברוש. התדעו כמה עצים במטע?
מתבסס על המשימה האוריינית מטע תפוחים משאלות מבחני פיזה.
כיתה: ט
תיאור: הישומון מופיע בפעילות: למצוא את הפתרון הטוב ביותר – חלק א העוסקת בבעיות ערך קיצון, אותן ניתן לפתור באמצעות מציאת קודקוד של פרבולה. בישומון ניתן לעקוב אחר השינוי בשטח הרצפה בצמוד לשינוי בגרף הפונקציה המתארת אותו.
כיתה: ט
תיאור: היישומון מופיע בפעילות: למצוא את הפתרון הטוב ביותר – חלק א העוסקת בבעיות ערך קיצון, אותן ניתן לפתור באמצעות מציאת קודקוד של פרבולה. הישומון מתאים לבעיה העוסקת בשטח של גינה. ניתן לעקוב אחר שינוי בשטח הגינה בצמוד לשינוי בגרף הפונקציה המתארת אותו.
כיתה: ט
תיאור: היישומון מופיע בפעילות: למצוא את הפתרון הטוב ביתר – חלק ב. פעילות זו עוסקת במציאת מלבן בעל שטח גדול ביותר. היישומון מאפשר לעקוב אחר השתנות שטח הגינה כאשר משנים את צלעותיה.
כיתה: ט
תיאור: היישומון מופיע בפעילות: למצוא את הפתרון הטוב ביותר – חלק ג. פעילות זו עוסקת בבעיות ערך קיצון, אותן ניתן לפתור באמצעות מציאת קודקוד של פרבולה. היישומון מראה את השתנות אורך קטע בין שתי נקודות על שתי פרבולות, כאשר גוררים את אחת הנקודות.
תיאור: אוסף משימות קצרות שמטרתן לחדד, להעמיק את ההבנה ולעורר שיח מתמטי בכיתה. המשימות מתאימות לתלמידי כיתה ט' ברמות הגבוהות. השאלות עוסקות בתכונות של פונקציות לפני חקירה – קדם אנליזה – כמו נקודות חיתוך עם הצירים, תחומי עלייה וירידה ונקודות קיצון, טרנספורמציות אלמנטריות של פונקציות. השאלות מתייחסות לגרפים של פונקציות ללא ביטויים אלגבריים.
תיאור: הפעילות עוסקת הכרות עם פונקציית הערך המוחלט ועם ההזזות שלה במקביל לציר ה- y. הגרף של פונקציית הערך המוחלט מורכב משתי קרניים – שני חלקים של קווים ישרים. על כן מתאים לגשר באמצעותו בין הפונקציה הקווית לפונקציה הריבועית. כאן אפשר להתחיל לדון במושגים: תחום עליה ותחום ירידה, ונקודת מינימום. הזזות, מתיחות ושיקוף ביחס לציר ה-x יובילו לגרפים שיהוו בסיס טוב להזזות, מתיחות ושיקוף ביחס לציר ה-x עבור הפונקציות הריבועיות. לפעילות זו יש פעילות המשך, העוסקת בהזזות במקביל לציר ה-x ומשלבת את שתי ההזזות.
תיאור: הפעילות עוסקת בהזזה האופקית של גרף הפונקציה ומתאימה לשילוב בהוראה לאחר ההיכרות עם משפחת הפונקציות ועם ההזזה האנכית. השאלה האחרונה בפעילות עוסקת בשילוב שתי ההזזות יחד: האנכית והאופקית. הפעילות מגשרת בין הפונקציה הקווית לפונקציה הריבועית ומציגה את מושג ההזזה על פונקציה פשוטה. באופן זה מורחב אוסף הפונקציות עליהן מבצעים את פעולות ההזזה ומוטמע מושג ההזזה במנותק מהפונקציה הריבועית.
תיאור: הפעילות עוסקת בפונקציות החזקה עם מעריך טבעי, והיא אחת מתוך אוסף פעילויות שמפגישות את התלמידים עם משפחות שונות של פונקציות, במטרה להכיר תכונות משותפות שיש לפונקציות במשפחות השונות, ולהעשיר את השפה המתמטית המאפשרת גם לתאר את תכונות הפונקציות, וגם להצדיקן לא על סמך מראה עיניים בלבד. ההיכרות עם פונקציות החזקה חשובה במיוחד, היות והן מהוות בסיס ללימודי האנליזה בכיתה יוד. לפעילות מצורף יישומון, שמציג את שתי הקבוצות של הפונקציות במשפחה זו לצד זו.
תיאור: פעילות זו עוסקת במשפחת הפונקציות (y=1/(x^n כאשר n מספר טבעי.
הגרפים של הפונקציות הללו מזמנים שיח מתמטי מעמיק בתכונות מיוחדות ומפתיעות עבור התלמידים: הם לא ניתנים לסרטוט במשיכת קולמוס אחת ו"נצמדים" לצירים.
מודגש כי הדיון במושגים: אי-רציפות ואסימפטוטות נעשה בשפה פשוטה שלא מערערת את הביטחון של התלמידים ביכולתם להבין הסברים מתמטיים ואין כוונה לעסוק במושגים אלה באופן מפורש ובאמצעות סימונים מתמטיים והגדרות מדוייקות.
הפעילות מלווה ביישומונים, אליהם ניתן להגיע גם באמצעות סריקת ברקוד, ומצורפים אליה גרפים שניתן לצלם עבור התלמידים, כדי לאפשר עבודה ללא מחשב.
תיאור: פעילות הפתיחה שלפניכם מפגישה את התלמידים, באמצעות שתי "מכונות" עם שתי טרנספורמציות פשוטות: האחת מבצעת, לכל נקודה על הגרף, שיקוף ביחס לציר ה-x, האחרת מבצעת שיקוף ביחס לציר ה-y. מבחינה אלגברית: האחת מתאימה לכל מספר את המספר הנגדי לזה המותאם בפונקציה המקורית, האחרת מתאימה לכל מספר את המספר שמותאם בפונקציה המקורית למספר הנגדי שלו.
מטרת הפעילות היא פיתוח יכולת זיהוי של גרף שהתקבל מהפעלה של שיקוף ביחס לאחד הצירים והתאמת הקשר האלגברי המתאים. העיסוק והדיון בתכונות הנשמרות והמשתנות בעקבות ההפעלה של כל אחת מהטרנספורמציות הנ"ל מעמיקים את ההבנה של מושג הפונקציה. לשיקול המורה קישור למושגים פונקציה זוגית ופונקציה אי-זוגית.
לפעילות מצורפים יישומונים.
תיאור: פעילות זו עוסקת בשיקופים של פונקציות ביחס לציר ה-x וביחס לציר ה-y. לתלמידים מוצגות שתי מכונות המבצעות את השיקופים. עליהם לחקור את התכונות שנשארות ואת התכונות שמשתנות תחת כל אחד מהשיקופים. לפעילות מצורף יישומון, בו אפשר להחליף פונקציות ולראות את השיקופים שלהן בעזרת סימון – "הראה גרף הפלט" או בעזרת סימון עקבות. התובנות שנרכשות באמצעות הפעילות מתווספות ל"ארגז הכלים" של התלמידים, כך שיוכלו להשתמש בהן עבור פונקציות אחרות. הפעילות מניחה בסיס גם להבנה של המושגים פונקציה זוגית ופונקציה אי-זוגית.
מומלץ לבצע פעילות זו אחרי פעילות הפתיחה "פונקציות מבעד למראה - שיקופים" המופיעה באתר המרכז הארצי למורים למתמטיקה בחינוך העל-יסודי.
תיאור: פעילות זו עוסקת במתיחה אנכית ובכיווץ אנכי של גרף של פונקציה. בהמשך לפעילות זו תוצע גם פעילויות העוסקת במתיחה אופקית ובכיווץ אופקי של גרף של פונקציה.
מטרות הפעילות הן:
- להעמיק את ההבנה של הקשר בין גרף פונקציה לבין גרף הפונקציה המתקבל מהכפלת ערכי הפונקציה בקבוע.
- לפתח "חוש לפונקציות".
- לזהות ולנתח פונקציות וגרפים של פונקציות באופן איכותני.
- להכיר ולהרחיב את מאגר הפעולות הנעשות על פונקציות.
- ליצור שיח מתמטי סביב המושג מתיחה אנכית וכיווץ אנכי של גרף של פונקציה כתשתית להבנת מושגים באנליזה.
תיאור: בעזרת יישומון זה ניתן לשקף גרף של פונקציה f(x) (פונקציית הקלט) ביחס לציר ה-y ולראות את הגרף המתקבל h(x) (פונקציית הפלט). אפשר להציג את גרף הפונקציה המתקבל משיקוף ביחס לציר ה-y או להסתירו ולבקש מהתלמידים לשער כיצד ייראה הגרף ואח"כ לבדוק בעזרת היישומון. אפשרות נוספת היא להשתמש ב"סרטוט באמצעות עקבות" ולעקוב אחר השיקוף של כל אחת מהנקודות שעל גרף הפונקציה הנתונה עד לקבלת הגרף שהוא שיקוף בציר ה-y .אפשר גם לשנות את הפונקציה הנתונה לכל פונקציה אחרת (פולינומית, רציונאלית, שורש, טריגונומטרית ועוד). בעזרת היישומון ניתן לנהל שיח כיתתי שיעסוק בחקר הקשר בין תכונות הגרפים של פונקציות לבין הגרפים של הפונקציות המתקבלים משיקוף ביחס לציר ה-y .לחילופין ניתן לחבר פעילויות לתלמידים שמנחות חקר כנ"ל ולשלב בהן את היישומון.
תיאור: בעזרת יישומון זה ניתן לשקף גרף של פונקציה f(x) (פונקציית הקלט) ביחס לציר ה-x ולראות את הגרף המתקבל g(x) (פונקציית הפלט). אפשר להציג את גרף הפונקציה המתקבל משיקוף ביחס לציר ה-x או להסתירו ולבקש מהתלמידים לשער כיצד ייראה הגרף ואח"כ לבדוק בעזרת היישומון. אפשרות נוספת היא להשתמש ב"סרטוט באמצעות עקבות" ולעקוב אחר השיקוף של כל אחת מהנקודות שעל גרף הפונקציה הנתונה עד לקבלת הגרף שהוא שיקוף בציר ה-x .אפשר גם לשנות את הפונקציה הנתונה לכל פונקציה אחרת (פולינומית, רציונאלית, שורש, טריגונומטרית ועוד). בעזרת היישומון ניתן לנהל שיח כיתתי שיעסוק בחקר הקשר בין תכונות הגרפים של פונקציות לבין הגרפים של הפונקציות המתקבלים משיקוף ביחס לציר ה-x .לחילופין ניתן לחבר פעילויות לתלמידים שמנחות חקר כנ"ל ולשלב בהן את היישומון.
תיאור: יישומון זה מציג גרפים של פונקציות מהמשפחה: y=x^n עם מעריך טבעי. הגרפים מוצגים בשני חלונות נפרדים, חלון לפונקציות עם מעריך זוגי וחלון לפונקציות עם מעריך אי-זוגי. היישומון מאפשר לנהל שיח כיתתי שיעסוק בתכונות משפחת פונקציות החזקה עם מעריך טבעי, על שני חלקיה. ניתן גם לחבר עבור התלמידים משימות שבהן משולב היישומון. דוגמאות למשימות המבוססות על יישומון זה אפשר למצוא בפעילות "פונקציית חזקה ממעלה זוגית וממעלה אי-זוגית".
תיאור: בעזרת יישומון זה ניתן להציג במערכת צירים אחת גרף של פונקציה f(x) וגרף של פונקציה g(x) המתקבלת ממנה על ידי הכפלתה בקבוע חיובי, כלומר g(x)=af(x). את ערכו של a אפשר לשנות באמצעות פס הגרירה. אפשר להחליף פונקציות ולראות את הייצוגים האלגבריים והגרפיים של הפונקציה המקורית ושל זו המתקבלת מהכפלתה בקבוע חיובי (a>0) בהתאם לערך של a תהיה זו מתיחה אנכית (a>1) או כיווץ אנכי (0<a<1). יש אפשרות להסתיר את הפונקציה המתקבלת מהמתיחה או מהכיווץ ולבקש מהתלמידים לשער כיצד ייראה הגרף שלה ואח"כ לבדוק בעזרת היישומון. אפשר לשנות את הפונקציה הנתונה לכל פונקציה אחרת (פולינומית, רציונאלית, שורש, טריגונומטרית ועוד). בעזרת היישומון ניתן לנהל שיח כיתתי שיעסוק בחקר הקשר בין תכונות הגרפים של פונקציות לבין הגרפים של הפונקציות המתקבלות מהכפלת ערכי הפונקציה בקבוע חיובי. לחילופין ניתן לחבר פעילויות לתלמידים שמנחות חקר כנ"ל ולשלב בהן את היישומון (ראו דוגמה בפעילות "מתיחה אנכית וכיווץ אנכי של גרף של פונקציה").
תיאור: יישומון זה מציג גרפים של פונקציות מהמשפחה: y=x^n עם מעריך שלם שלילי. הגרפים מוצגים בשני חלונות נפרדים, חלון לפונקציות עם מעריך זוגי וחלון לפונקציות עם מעריך אי-זוגי. היישומון מאפשר לנהל שיח כיתתי שיעסוק בתכונות משפחת פונקציות זו, על שני חלקיה. ניתן גם לחבר עבור התלמידים משימות שבהן משולב היישומון. דוגמאות למשימות המבוססות על יישומון זה אפשר למצוא בפעילות "משפחת הפונקציות: y=1/x^n מעריך טבעי".

![]() הרחבת עולם הפונקציות לתלמיד|
הרחבת עולם הפונקציות לתלמיד| ![]() הרחבת עולם הפונקציות למורה|
הרחבת עולם הפונקציות למורה| ![]() لطالب باللغة العربية
لطالب باللغة العربية
יחידת לימוד לכיתה המדעית.
ביחידה זו נעסוק בהרחבה ובהעמקה של מושג הפונקציה. בפרט נחקור הזזות ומתיחות של פונקציות שונות. נתחיל בהכרות של הזזות ומתיחות בהקשר של בעיות אורייניות, בעיות מילוליות המתארות מצבים מחיי היום יום. נבחן את המשמעות של הזזות ומתיחות של פונקציות בגרפים ובביטויים האלגבריים. בהמשך נתבונן בהזזות ומתיחות של גרפים שונים, שלא בהכרח אנו מכירים את התבנית האלגברית שלהן. נבחין בין פעולות אנכיות לאופקיות. בחלק האחרון של היחידה, נכיר את פונקצית השורש כפונקציה ההפוכה לפונקציה הריבועית, ושוב נעמיק ונחקור כיצד באות לידי ביטוי פעולות ההזזות והמתיחות על פונקצית השורש. במהלך היחידה מומלץ (אך לא הכרחי) להשתמש ביישומונים הדינאמיים המשולבים ביחידה, המאפשרים לראות את פעולת ההזזות והמתיחות באופן חזותי ומוחשי וכתנועה חיה של הגרפים.
כיתה: ט - י
תיאור: היישומון מופיע בפעילות: פונקציות מבעד למראה – שיקופים ביחס לצירים. היישומון מאפשר התבוננות בגרף של פונקציה המתקבל מגרף אחר באמצעות שיקוף בציר X. ההתבוננות יכולה להיות נקודתית (עקבות) או כללית. היישומון מצורף לפעילות שמפגישה את התלמידים, באמצעות שתי "מכונות", עם שתי טרנספורמציות פשוטות: האחת מבצעת שיקוף ביחס לציר ה-X. האחרת מבצעת שיקוף ביחס לציר ה- Y.
כיתה: ט - י
תיאור: היישומון מופיע בפעילות: פונקציות מבעד למראה – שיקופים ביחס לצירים. היישומון מאפשר התבוננות בגרף של פונקציה המתקבל מגרף אחר באמצעות שיקוף בציר Y. ההתבוננות יכולה להיות נקודתית (עקבות) או כללית. היישומון מצורף לפעילות שמפגישה את התלמידים, באמצעות שתי "מכונות", עם שתי טרנספורמציות פשוטות: האחת מבצעת שיקוף ביחס לציר ה-X. האחרת מבצעת שיקוף ביחס לציר ה- Y.
כיתה: י' או י"א
תיאור: היישומון מופיע בפעילות: אל הגרף של פונקציית השורש הריבועי, בה פונקציית השורש הריבועי והגרף שלה מוצגים באמצעות הקשר ביניהם לבין הענף החיובי של הפונקציה .y=x^2 ההיכרות עם הקשרים בין שתי הפונקציות האלה זורעת זרעים לקראת פעילות המשך, העוסקת בין הנגזרות של שתי הפונקציות האלה. ביישומון הדינמי גוררים נקודה על גרף הפונקציה y = x^2 ורואים את שיעורי הנקודה המתקבלת ממנה באמצעות שיקוף בישר y=x.
כיתה: י - י"א
תיאור: יישומון זה מאפשר לנהל שיח כיתתי על תכונות של פונקציות שהן הרכבה של פונקציות חזקה עם מעריך טבעי (x^n) על פונקציה אחרת, כלומר פונקציות מהצורה: (f(x)^n), n מספר טבעי, ועל הקשר בין פונקציות אלה לבין הפונקציות הפנימיות שלהן. היישומון מאפשר, באמצעות סרגל גרירה לשנות את המעריך ולדון בתכונות שמאפיינות גרפים המתקבלים ממעריכים זוגיים לעומת תכונות של גרפים שמתקבלים ממעריכים אי-זוגיים.
כיתה: ט - י
תיאור: היישומון מאפשר לנהל שיח כיתתי שיעסוק בתכונות משפחת פונקציות זו, על שני חלקיה. ניתן גם לחבר עבור התלמידים משימות שבהן משולב היישומון. דוגמאות למשימות המבוססות על יישומון זה אפשר למצוא בפעילות "משפחת הפונקציות y=1/x^n מעריך טבעי".
כיתה: ט – י
תיאור: בעזרת היישומון ניתן לנהל שיח כיתתי שיעסוק בחקר הקשר בין תכונות הגרפים של פונקציות לבין הגרפים של הפונקציות המתקבלות מהכפלת ערכי הפונקציה בקבוע חיובי. לחילופין ניתן לחבר פעילויות לתלמידים שמנחות חקר כנ"ל ולשלב בהן את היישומון (ראו דוגמה בפעילות "מתיחה אנכית וכיווץ אנכי של גרף של פונקציה").
כיתה: ט – י
תיאור: יישומון זה מציג גרפים של פונקציות מהמשפחה: y=x^n עם מעריך טבעי. הגרפים מוצגים בשני חלונות נפרדים, חלון לפונקציות עם מעריך זוגי וחלון לפונקציות עם מעריך אי-זוגי. היישומון מאפשר לנהל שיח כיתתי שיעסוק בתכונות משפחת פונקציות החזקה עם מעריך טבעי, על שני חלקיה. ניתן גם לחבר עבור התלמידים משימות שבהן משולב היישומון. דוגמאות למשימות המבוססות על יישומון זה אפשר למצוא בפעילות "פונקציית חזקה ממעלה זוגית וממעלה אי-זוגית".
כיתה: ט – יא
תיאור: בעזרת יישומון זה ניתן לשקף גרף של פונקציה f(x) (פונקציית הקלט) ביחס לציר ה- x ולראות את הגרף המתקבל g(x) )פונקציית הפלט(.
כיתה: ט – י
תיאור: בעזרת יישומון זה ניתן לשקף גרף של פונקציה f(x) (פונקציית הקלט) ביחס לציר ה- Y ולראות את הגרף המתקבל g(x) )פונקציית הפלט(.
לפניכם יחידת לימוד העוסקת בקריאת גרפים ומיועדת לתלמידי כיתות ח' ו-ט'. המשימות עוסקות בנושאים שונים, בחלקן מכילות יישומונים.
להלן סדר הפעילויות המתאים לעבודה באמצעות היחידה:
- טבלה וגרף
- מצגת: טבלה וגרף / بالعربية
- טבלה וגרף - הכנסה כספית - גרף משולב מכמה קטעי גרפים
- מצגת: גרף משולב מכמה מקטעי גרפים - צריכת סוכר / بالعربية
- גרף משולב מכמה מקטעי גרפים - השוואה בין גרפים
- מצגת: השוואה בין גרפים - נשים וגברים באקדמיה / بالعربية
- השוואה בין גרפים – משימה: מרחק מכדור הארץ - משימות מסכמות - גרף משולג והשוואה בין גרפים
- משימה מסכמת 1 – גרף משולב והשוואה בין גרפים – ממוצע ציונים
- משימה מסכמת 2 – גרף משולב והשוואה בין גרפים – אימון ריצה
תיאור: יישומון דינאמי ודף עבודה המציעים חקר וגילוי במשימה האוריינית דרגשי העץ.
המשימה מיועדת לכיתה ז ומשלבת את התחום האלגברי והגיאומטרי על תכונות המלבן והריבוע כולל שטח והיקף. ניתן לשנות את מימדי הספסל ולאסוף נתונים בטבלה.
היישומון מלווה בשאלות אינטראקטיביות.
יישומון דרגשי העץ בהפקת אלנט עבור אגף טכנולוגיות מידע במשרד החינוך.
 מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
אופי הפעילות: יישום דינאמי.
תאור: ביישום הדינאמי יש להוכיח כי קיים מלבן ששטחו שווה לשטח המקבילית. או במילים אחרות המחשה לכך ששטח כל המקביליות עם צלע נתונה (a) וגובה נתון (h) שווה, והוא שווה לשטח המלבן שאורך צלעותיו כצלע המקבילית והגובה.
מקור: אתר הפייסבוק של עידן טל
אופי הפעילות: תמונה דינאמית ממחישה ומעוררת דיון כיתתי.
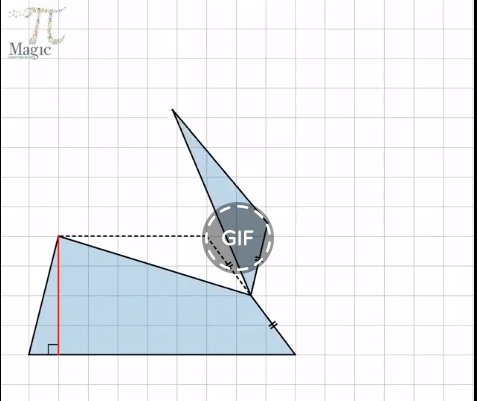
תיאור: התמונה הדינמית תומכת בהצמחה של נוסחת שטח משולש: מחצית מכפלת אורך של צלע באורך הגובה אליה במשולש ע"י מעבר ממשולש למלבן ששטחו בדיוק כפליים משטח המשולש.
* אין לשכוח שתמונה דינאמית אינה מספקת הוכחה. יש להשלים הוכחה מדויקת בסיום הדיון שמתקיים בכיתה בעקבות הצפייה בתמונה הדינאמית.
 מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
תאור: דף עבודה אינטראקטיבי בו מוצגים מלבנים שווי שטח בהם חסומים צורות שונות. על התלמיד למצוא את השטח הצבוע הגדול ביותר והקטן ביותר על פי חישובי שטח משולש עם גבהים שווים. המשימה לקוחה מתוך מתמטיקה משולבת כיתה ז.
 מקור: NASA STI Program
מקור: NASA STI Program
תאור: סרט באורך 25 דקות, מבית היוצר של NASA, מתוך "פרוייקט מתמטיקה". בסרט מוצגת ההיסטוריה של המספר פאי ושימושיו השונים, בפרט במדעי המחשב.
 מקור: minutephysics
מקור: minutephysics
תאור: סרטון אנימציה חביב המציג הוכחה, כמעט ללא מילים של הנוסחה לשטח עגול והקבלתה של הנוסחה לשטח משולש.
 מקור: mathematicsonline
מקור: mathematicsonline
תאור: סרטון קצר המציג הוכחה לנוסחת שטח העיגול ע"י חילוק המעגל לגזרות ובנייה מחדש מהן מלבן בעל שטח שווה.
 מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
תאור: הפיצוח מוקדש באהבה למורי ולתלמידי המתמטיקה, בפעילות קצת אחרת העוסקת בצורה ההנדסית ממנה מורכב האיור המוכר של הלב. בפעילות יש צורך בהכרת המצולעים והמעגל ובחישוב שטחיהם.
 מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
תאור: הפיצוח "מעגלי ארכימדס" מספר על ארכימדס ועל חקר צורות מעגליות הארבלוס והסולינון. מומלץ לשלב את הפעילות בלימודי הגיאומטריה בנושא תכונות המעגל ושטחו.
 מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
תאור: בפיצוח מוצגות צורות גאומטריות בעיצוב של פרחים. המשימה דורשת יכולת ניתוח בניית הצורה וחישובי שטחים של מעגלים ומצולעים. המשימה בנוייה ברמות קושי הולכות ועולות ומתאימה לתלמידים החל מכיתה ז' ועד יב'.
מצורף גם סרטון ליצירה של עטיפה משושה ופרחונית לדיסק.
 מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
תאור: הפיצוח משלב פעילות יצירתית וחקירה מתמטית. בפיצוח הוראות לבנייה בסרגל ומחוגה, או בעזרת תוכנה גיאומטרית כגון גאוגברה, של שרטוט מעגלים היוצרים פרח משושה מרהיב. הפעילות כוללת חקירת הבנייה וחישובי שטחים. הידע הנדרש: שטח מעגל וגזרה, משולש שווה צלעות ושטחו, משפט פיתגורס.
 מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
תאור: בפיצוח שלש בעיות בגיאומטריה, המוצגות כחידות, הדורשות דמיון וראייה מרחבית. היישומים הדינאמיים מסייעים להמחשה ולפיתוח חשיבה ויזואלית. הבעיות מתאימות ללומדים את נושא המעגל כמקום גיאומטרי (לאו דוקא באופן אלגברי) והכרות עם חישובי שטח של עיגול.
 מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
תאור: בפיצוח שלש בעיות, חידות קצרות, העוסקות בהיקף ובשטח מעגל המתאימות לתלמידי כיתה ז' ומעלה. הפעם צירפנו גם פתרונות.
 מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
תאור: ב14 למרץ חוגגים ברחבי העולם לכבודו של המספר המופלא ∏. בפיצוח פעילויות הנוגעות בחישוב היקף ושטח מעגל אשר ניתן לשלבן בחגיגות. בפעילות הסבר במלל ובסרטים על המספר וסקירה קצרצרה על התפתחותו.
 מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
תאור: יישום דינאמי המציג באופן ויזואלי את שיטתו של ארכימדס לחישוב פאי. ארכימדס הציג לראשונה שיטה המאפשרת לחשב את פאי בכל רמת דיוק שתידרש. שיטתו מתבססת על כך שהיקף המעגל קטן מהיקפו של מצולע החוסם
מעגל וגדול מהיקפו של מצולע החוסם מעגל. באמצעות חישוב ההיקף של מצולע חוסם ומצולע חסום בעלי מספר הולך וגדל של צלעות נשיג דיוק גדל והולך של היקף המעגל, ובהתאם לכך דיוק גדל והולך של פאי (ויקיפדיה).
קראו עוד בהרחבה על סיפורו של פאי.
 מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
תאור: יישום דינאמי לחקירה והמחשה של מציאת הנוסחאות להיקף ושטח מעגל. החישוב המקורב לשטח העיגול נמצא לפי חלוקה למספר רב של גזרות והרכבתן מחדש לצורה המתקרבת להיות מלבן.
צפו בסרט: the story of Pi בו תוכלו לראות המחשות לנוסחת שטח מעגל.
עיינו גם בפיצוח יום פאי שמח.
תיאור: אוסף משימות בנושא של סוגי זוויות המכיל פעילויות מיון קצרות המחדדות הבנה. המשימות מתאימות לתלמידי כיתות ז' ברמות השונות ומאפשרות לכל תלמיד בכיתה לענות עליהן בהתאם ליכולותיו.
 מקור: הילקוט הדיגיטלי של מטח לחט"ב
מקור: הילקוט הדיגיטלי של מטח לחט"ב
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: יחידת לימוד אינטראקטיבית לזיהוי זוויות קדקודיות הכוללת ישומים דינאמיים ושאלות עם משוב אינטראקטיבי.
 מקור: ebaghigh
מקור: ebaghigh
אופי הפעילות: יישום דינאמי
תאור: דף עבודה אינטראקטיבי ויישומון דינאמי לחקירה של מצבים שונים של זווית בין חוצי זווית של זוויות בעלי שוק משותפת.
 מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
תיאור: יישום דינאמי המספק המחשה לשיוויון בין זוויות מתחלפות שנוצרות בין ישרים מקבילים וחותך.

מקור: אתר הפייסבוק של עידן טל
אופי הפעילות: תמונה דינאמית ממחישה ומעוררת דיון כיתתי
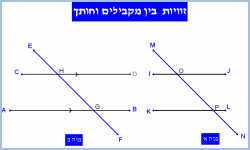
תיאור: בתמונה הדינאמית מוצגים שני ישרים וישר שלישי שחותך אותם. ומסומנות 8 הזויות הנוצרות בחיתוכים. המצב ההדדי בין הישרים משתנה עד למקבילות בין שני הישרים.
באמצעות צבעים שונים מומחש שוויון הזווית במצב של מקבילות בלבד.
* אין בתמונה הדינאמית הוכחה או הכוונה להוכחה.
 מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
תאור: דף עבודה ויישום דינאמי לחקירה וגילוי של המשפטים על זוויות הנוצרות בין חותך למקבילים.
ביישום מופיע זוג אחד של ישרים, שאינם בהכרח מקבילים וחותך, וזוג אחד של ישרים מקבילים וחותך.
בכל אחד מהזוגות והחותך יש אפשרות לבדיקה והשוואה בין הזוויות שנוצרות בין החותך לבין הישרים, כך שניתן לגלות את התכונות המיוחדות של הזוויות הנוצרות במצב בו הישרים מקבילים.
 מקור: Learn Zillion
מקור: Learn Zillion
תאור: שיעור מתוך סדרת שיעורים בנושא ובו סרטון ומצגת הניתנת להורדה (ולתרגום), המציג בדרך ידידותית והמחשות ויזואליות את הזוויות בין מקבילים ופתרון בעיות שונות בעזרת המשפטים.
 מקור: מתמטיקה עמקים תבור – כיתה ז שיעורים מוקלטים
מקור: מתמטיקה עמקים תבור – כיתה ז שיעורים מוקלטים
תאור: "שיעור הפוך" של מירטה לוין ובו סרטון המציג את המושגים והמשפטים של זוויות בין מקבילים וחותך ומבדק אינטראקטיבי בו אוסף שאלות ממתמטיקה משולבת ואפשר גם אחרת.
 מקור: מרכז מורים ארצי למתמטיקה בחינוך העל יסודי
מקור: מרכז מורים ארצי למתמטיקה בחינוך העל יסודי
תאור: דף עבודה אינטראקטיבי ויישום דינאמי לגילוי וחקירה של זוויות במצולע משוכלל בעל n צלעות.

מקור: אתר הפייסבוק של עידן טל
אופי הפעילות: תמונה דינאמית ממחישה ומעוררת דיון כיתתי
תיאור: התמונה הדינאמית ממחישה את הסכום הקבוע (360 מעלות) לזוויות החיצוניות בכל מצלולע קמור.
* אין לשכוח שתמונה דינאמית אינה מספקת הוכחה. יש להשלים הוכחה מדויקת בסיום הדיון שמתקיים בכיתה בעקבות הצפייה בתמונה הדינאמית.
 מקור: illuminations
מקור: illuminations
תאור: יישומון דינאמי בו ניתן לחקור ולגלות את הנוסחה לסכום זוויות במצולע כלשהו. היישום מציג את מידות הזוויות הפנימיות ואת סכומן. ניתן לשנות את מימדי המצולע ולצפות כיצד סכום הזוויות נשאר קבוע.
 מקור: geogebraTube, Orcheming
מקור: geogebraTube, Orcheming
תאור: יישום דינאמי לחקירת סכום זוויות חיצניות במצולע כלשהו. ביישום מכונית נוסעת על שפת מצולע מחומש ומסתובבת סביב כל קודקוד. מהו סכום זוויות שהמכונית הסתובבבה? ניתן לשנות את מימדי המחומש.
 מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
תאור: יישום דינאמי הממחיש באופן ויזואלי את אחת ההוכחות למשפט סכום הזוויות במשולש 180º.
 מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
תאור: בפיצוח גילוי והוכחה בעזרת קיפולי נייר לסכום הזוויות במשולש. ועוד קיפולים גיאומטרים רבים ויפים אחרים.
 מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
תאור: מאמר בעל"ה 43, מאת נצה מובשוביץ-הדר וג'רי רוזן
תרגום ועיבוד של המאמר: "The angels sum of a triangle" ,שפורסם בכתב עת בריטי בשנת 1992. הוא עוסק בסכום הזוויות במשולש, אך לא בגיאומטריה האוקלידית במישור.
 מקור: illuminations
מקור: illuminations
תאור: פעילות אינטראקטיבית לחקירה מהו סכום הזוויות במשולש, במרובע , מחומש והכללתו למצולע בעל n צלעות. כולל סרטוני אנימציה קצרים (למטה מימין) להמחשת ההוכחה במשולש ובמרובע.
 מקור: מתמטיקה משולבת
מקור: מתמטיקה משולבת
תאור: דף עבודה אינטראקטיבי (גאוגברה), לבדיקה וחקירה של סכום הזוויות במשולש. דף עבודה נוסף גם בנושא סכום זוויות במרובע
 מקור: UCSMP
מקור: UCSMP
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: יחידת לימוד אינטראקטיבית לזיהוי זוויות קדקודיות הכוללת ישומים דינאמיים ושאלות עם משוב אינטראקטיבי.
 מקור: גלים – לומדים גיאומטריה עם כלי גאוגברה
מקור: גלים – לומדים גיאומטריה עם כלי גאוגברה
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: יחידת לימוד אינטראקטיבית ובה יישומים דינאמיים בגאוגברה ושאלות לתלמיד עם משוב. היחידה עוסקת בבניית משולשים לפי צלעות (מהתכונה לצורה).
 מקור: מרכז מורים ארצי למתמטיקה בחינוך העל יסודי
מקור: מרכז מורים ארצי למתמטיקה בחינוך העל יסודי
אופי הפעילות:
תאור: דף עבודה אינטראקטיבי ויישומון דינאמי לחקירה של אי שוויון המשולש. בהנתן שלשה של אורכי צלעות, האם ניתן לבנות מהם משולש?
תיאור: אוסף המשימות שלפניכם עוסק בחפיפה ודמיון של משולשים ומיועד לתלמידים בכיתות ח'. בקובץ יש התייחסות גם למשפט פיתגורס. השאלות מדורגות, מתחילות במשימות פשוטות ומתפתחות למשימות מורכבות יותר, כך שהן יכולות להתאים לתלמידים ברמות שונות.
הפעילות עוסקת בגיאומטריה חישובית בהקשר של חפיפת משולשים בבעיות אורייניות. הנתונים במשימות נמסרים באמצעות תיאור מצב מחיי היום-יום (לדוגמה מרחק בין צמתים) ולא "מוגשים" באופן ישיר באמצעות שמות של נקודות או שיוויון בין אורכי קטעים, אלא מסתתרים בתוך הכתוב. אי לכך, נדרש תהליך של קריאה יסודית ופיענוח של הנתונים מתוך הסיטואציה המתוארת.
המשימות מתאימות לתלמידי כיתה ח' ברמות הנמוכות, אך ניתן, כמובן, להיעזר בהן גם בראשית ההוראה של הנושא, גם ברמות הגבוהות יותר.
תיאור: פעילות זו היא אחת מתוך 3 פעילויות שעוסקות במשפט החפיפה הרביעי: צ.צ.ז. שילובן מתאים לאחר שלומדים על משפט פיתגורס. בתחילת כיתה ח לומדים את שלושת משפטי החפיפה הראשונים: צ.ז.צ, ז.צ.ז, צ.צ.צ.
לאחר שמכירים את משפט פיתגורס, מוכיחים מקרה פרטי של משפט החפיפה הרביעי: שני משולשים ישרי זווית השווים בניצב וביתר חופפים זה לזה. מייד לאחר מכן מתאים להכיר גם את המקרה הכללי של משפט החפיפה הרביעי – צ.צ.ז (הזווית מול הצלע הגדולה בין השתיים). ההכרות היא ללא הוכחה לעת עתה. בכיתה ט' יחזרו התלמידים אל המשפט ויוכיחו אותו בדרך השלילה, כאשר יעסקו במשפטים שדנים באי-שוויונות במשולש. ההכרות עם המשפט בכיתה ח' אינה דדוקטיבית.
הפעילות הראשונה ביחידה עוסקת בשאלת החשיבות של סדר הנתונים השווים בין שני משולשים ושל מספר הנתונים השווים.
הפעילות השנייה ביחידה חושפת את משפט החפיפה הרביעי ומשלבת שימוש ביישומון.
הפעילות השלישית היא פעילות תרגול.
תיאור: פעילות זו היא אחת מתוך 3 פעילויות שעוסקות במשפט החפיפה הרביעי: צ.צ.ז. שילובן מתאים לאחר שלומדים על משפט פיתגורס. בתחילת כיתה ח לומדים את שלושת משפטי החפיפה הראשונים: צ.ז.צ, ז.צ.ז, צ.צ.צ.
לאחר שמכירים את משפט פיתגורס, מוכיחים מקרה פרטי של משפט החפיפה הרביעי: שני משולשים ישרי זווית השווים בניצב וביתר חופפים זה לזה. מייד לאחר מכן מתאים להכיר גם את המקרה הכללי של משפט החפיפה הרביעי – צ.צ.ז (הזווית מול הצלע הגדולה בין השתיים). ההכרות היא ללא הוכחה לעת עתה. בכיתה ט' יחזרו התלמידים אל המשפט ויוכיחו אותו בדרך השלילה, כאשר יעסקו במשפטים שדנים באי-שוויונות במשולש. ההכרות עם המשפט בכיתה ח' אינה דדוקטיבית.
הפעילות הראשונה ביחידה עוסקת בשאלת החשיבות של סדר הנתונים השווים בין שני משולשים ושל מספר הנתונים השווים.
הפעילות השנייה ביחידה חושפת את משפט החפיפה הרביעי ומשלבת שימוש ביישומון.
הפעילות השלישית היא פעילות תרגול.
תיאור: פעילות זו היא אחת מתוך 3 פעילויות שעוסקות במשפט החפיפה הרביעי: צ.צ.ז. שילובן מתאים לאחר שלומדים על משפט פיתגורס. בתחילת כיתה ח לומדים את שלושת משפטי החפיפה הראשונים: צ.ז.צ, ז.צ.ז, צ.צ.צ.
לאחר שמכירים את משפט פיתגורס, מוכיחים מקרה פרטי של משפט החפיפה הרביעי: שני משולשים ישרי זווית השווים בניצב וביתר חופפים זה לזה. מייד לאחר מכן מתאים להכיר גם את המקרה הכללי של משפט החפיפה הרביעי – צ.צ.ז (הזווית מול הצלע הגדולה בין השתיים). ההכרות היא ללא הוכחה לעת עתה. בכיתה ט' יחזרו התלמידים אל המשפט ויוכיחו אותו בדרך השלילה, כאשר יעסקו במשפטים שדנים באי-שוויונות במשולש. ההכרות עם המשפט בכיתה ח' אינה דדוקטיבית.
הפעילות הראשונה ביחידה עוסקת בשאלת החשיבות של סדר הנתונים השווים בין שני משולשים ושל מספר הנתונים השווים.
הפעילות השנייה ביחידה חושפת את משפט החפיפה הרביעי ומשלבת שימוש ביישומון.
הפעילות השלישית היא פעילות תרגול.
 מקור: מתמטיקה משולבת
מקור: מתמטיקה משולבת
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: אוסף פעילויות בגאוגברה לחקירת משולשים חופפים.
משולש שווה שוקיים חופף למשולש נתון
משולש חופף למשולש נתון לפי צ.ז.צ.
 מקור: National library of Virtual manipulatives
מקור: National library of Virtual manipulatives
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: יישום אינטראקטיבי בו המשימה היא לבנות שני משולשים חופפים לפי משפטי החפיפה השונים. משולש אחד ניתן בכחול והשני באדום. יש לחבר את הצלעות לזווית עד להשלמת המשולש. היישום נותן משוב האם שני המשולשים שבניתם אכן חופפים.
 מקור: מרכז מורים ארצי למתמטיקה בחינוך העל יסודי
מקור: מרכז מורים ארצי למתמטיקה בחינוך העל יסודי
אופי הפעילות: יישום דינאמי
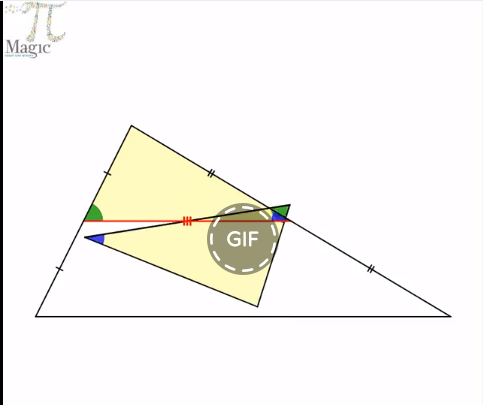
תאור: יישום דינאמי בו מוצגת בעיה גיאומטרית פתוחה. על אחת מצלעות המלבן בנו משולש שווה שוקיים כך שהקטע הנוצר בצלע המקבילה במלבן הוא קטע אמצעים של המשולש. על פי האיור יש למצוא יחסי שטחים שונים.

מקור: אתר הפייסבוק של עידן טל
אופי הפעילות: תמונה דינאמית ממחישה ומעוררת דיון כיתתי
תיאור: התמונה הדינאמית ממחישה את ההתלכדות של הגובה לבסיס במשולש שווה שוקיים עם התיכון לבסיס ועם חוצה זווית הראש.
* אין לשכוח שתמונה דינאמית אינה מספקת הוכחה. יש להשלים הוכחה מדויקת בסיום הדיון שמתקיים בכיתה בעקבות הצפייה בתמונה הדינאמית.
 מקור: מרכז מורים ארצי למתמטיקה בחינוך העל יסודי
מקור: מרכז מורים ארצי למתמטיקה בחינוך העל יסודי
אופי הפעילות: יישום דינאמי
תאור: דף עבודה ויישום דינאמי עם הנחיות לבניית משולש שווה שוקיים בגאוגברה בשלש דרכים שונות, על פי תכונות משולש שווה שוקיים.
 מקור: מרכז מורים ארצי למתמטיקה בחינוך העל יסודי
מקור: מרכז מורים ארצי למתמטיקה בחינוך העל יסודי
אופי הפעילות: יישום דינאמי
תאור: דף עבודה ויישום דינאמי עם הנחיות לבניית משולש שווה צלעות, האחת עם כלי מוכן של גאוגברה והשניה בדרך של בניה עם סרגל ומחוגה.
 מקור: moremathgrads' channel
מקור: moremathgrads' channel
אופי הפעילות: סרטון המסביר כיצד ניתן לקפל משולש שוקיים צלעות מנייר מלבני.
תאור: התדעו להסביר מדוע מתקבל משולש שווה שוקיים? סרטון המראה קיפול נייר למשולש שווה שוקיים.
 מקור: moremathsgrads' channel
מקור: moremathsgrads' channel
אופי הפעילות: סרטון המסביר כיצד ניתן לקפל משולש שווה צלעות מנייר מלבני.
תאור: התדעו להסביר מדוע מתקבל משולש שווה צלעות? סרטון המראה קיפול נייר למשולש שווה צלעות בשני קיפולים בלבד.
 מקור: גלים – לומדים גיאומטריה עם כלי גאוגברה
מקור: גלים – לומדים גיאומטריה עם כלי גאוגברה
אופי הפעילות: חקר באמצעות יישומים דינאמיים
תאור: יחידת לימוד אינטראקטיבית ובה יישומים דינאמיים בגאוגברה ושאלות לתלמיד עם משוב. היחידה עוסקת בבניית משולשים לפי צלעות (מהתכונה לצורה).
 מקור: גאוגברה
מקור: גאוגברה
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: סרטוט דינמי המאפשר חקירה כהקדמה להוכחה. הועלה בהקשר לשאלה מתוך שבילים לכיתה ח
תיאור: אוסף המשימות שלפניכם עוסק בחפיפה ודמיון של משולשים ומיועד לתלמידים בכיתות ח'. בקובץ יש התייחסות גם למשפט פיתגורס. השאלות מדורגות, מתחילות במשימות פשוטות ומתפתחות למשימות מורכבות יותר, כך שהן יכולות להתאים לתלמידים ברמות שונות.
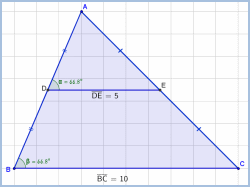
תיאור: המשימות בפעילות עוסקות בגיאומטריה חישובית בהקשר של מצבים מחיי היום-יום. בפתרון המתמטי מודגש השימוש בדמיון משולשים, לצד שימוש במשפט פיתגורס, אחוזים ויחידות מידה. המשימות נכתבו בשתי גרסאות, כך שניתן להתאימן לתלמידים ברמה המצומצמת או לתלמידים ברמה הגבוהה יותר.

אופי הפעילות: יישומים דינאמיים.
תיאור: אוסף פעילויות אינטרקטיביות בגאוגברה בנושא דמיון משולשים ומצולעים, קנה מידה ופרופורציות.
 מקור: מרכז מורים ארצי למתמטיקה בחינוך העל יסודי
מקור: מרכז מורים ארצי למתמטיקה בחינוך העל יסודי
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: דף עבודה ויישום דינאמי
 מקור: מרכז מורים ארצי למתמטיקה בחינוך העל יסודי
מקור: מרכז מורים ארצי למתמטיקה בחינוך העל יסודי
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: יישום דינאמי לדיון וחקירה של המשפט: הגובה במשולש ישר זווית שווה לממוצע הגיאומטרי של היטליו.
 מקור: מרכז מורים ארצי למתמטיקה בחינוך העל יסודי
מקור: מרכז מורים ארצי למתמטיקה בחינוך העל יסודי
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: דף עבודה ויישום דינאמי העוסק במשפט קטע אמצעים במשולש. דף העבודה מטפל בתכונות קטע אמצעים במשולש ובתנאים המספיקים וההכרחיים לקיומו.
 מקור: Illuminations - NCTM
מקור: Illuminations - NCTM
אופי הפעילות: חקירה אינטראקטיבית של מלבנים דומים , כיצד משתנה יחס הצלעות,יחס ההיקפים, ויחס השטחים . בפעילות נלווית ניתן גם לחקור את הגרפים של שינוי ההיקפים והשטחים במלבנים דומים. חקירה אינטראקטיבית של תיבות דומות , יחס המקצועות, שטחי פנים, הנפחים.
 מקור: LearnZillion
מקור: LearnZillion
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: סרטון ומצגת לשימוש בדמיון משולשים ישרי זווית לפתרון הבעיה – כיצד מוצאים את גובה הבניין. במצגת הסבר כללי על דמיון משולשים לפי זוויות, דוגמאות חישוביות והתייחסות לטעויות נפוצות. מצורף גם מדריך למורה.
 מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: דף עבודה אינטראקטיבי ובו בודקים מהו התנאי המספיק לדמיון משולשים והוכחתו.
 מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: דף עבודה ויישום דינאמי לחקירה וגילוי של היחסים במשפט תאלס והנחיות להוכחתו.

מקור: מרכז מורים ארצי למתמטיקה בחינוך העל יסודי
אופי הפעילות: חקר בעזרת יישום דינאמי
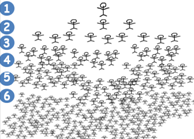
תיאור: פיצוח המתאר את בניית פרקטל צעד אחר צעד ומציאת תבניות של חוקיות.

מקור: מרכז מורים ארצי למתמטיקה בחינוך העל יסודי
אופי הפעילות: חקר בעזרת יישום דינאמי
תיאור: בפיצוח הזמנה להשתתף בפרויקט בינלאומי למדידת היקף כדור הארץ באותן שיטות ועקרונות פשוטים ומדהימים שהשתמש בהם ארטוסתנס לפני יותר מ-2000 שנה. ביום ה-22 בספטמבר, תלמידים מרחבי העולם יבצעו את המדידה וישתפו זה את זה בתוצאותיהם.
בפיצוח הסבר על הפרויקט ואופן ביצועו וכן הסברים על שיטתו של ארטוסתנס הכוללים איורים וסרטים ממחישים.
הידע הבסיסי הנדרש לפעילות הוא מעט גיאומטריה.
 מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: פיצוח ובו חקירת מלבנים דומים. במשימה האינטראקטיבית מתבקשים התלמידים למצוא מלבנים דומים בתמונה של הצייר מונדריאן. ביישום הדינאמי ניתן להזיז, לסובב ולשנות את מימדי המלבנים. המשך
הפיצוח ציור באדום, כחול וצהוב ובו קישוריות בין אמנות וגיאומטריה.

מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
אופי הפעילות: פיצוח - חקר בעזרת יישום דינאמי של NCTM
תאור: פיצוח ובו חקירה אינטראקטיבית של החוקיות של מספר הפגיעות הכדור בשולחן הביליארד.דרך משחק חוקרים מלבנים דומים, יחס הדמיון ומציאת המחלק המשותף הגדול ביותר, והמכפלה המשותפת הקטנה ביותר.
מומלץ גם לעיין במצגת "מפצחים את הדמיון" ודף פעילות , מאת מיכל מלר בכנס המורים 2010.
 מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: פיצוח ובו חקירת משולשים ומלבנים דומים הנוצרים בעזרת הגדלה והקטנה. הפיצוח מאפשר חקירה אינטראקטיבית של יחס הדמיון בצורות דומות, יחס ההיקפים ויחס השטחים.
מקור: מרכז מורים ארצי למתמטיקה בחינוך העל יסודי
אופי הפעילות: חקר בעזרת יישום דינאמי
תיאור: בפיצוח זה נצא למסע בעבר, בתקופות שונות ברחבי העולם מצריים, הודו וסין השתמשו במושג הדמיון לפתרון בעיות הנדסיות שונות.
הבעיות ברמות חשיבה שונות ומזמנות את התלמידים לחקור ולקשר לחיי היום יום ולהיסטוריה של המתמטיקה.

אופי הפעילות: סרטון מונפש ושיעור אינטראקטיבי
תאור: סרטון מונפש מביתTED Ed המספר את הרקע ההיסטורי והמתמטי של משפט פיתגורס, ומציג כמה מההוכחות היפות של משפט פיתגורס. הסרטון מלווה במדריך למורה, שאלון אינטראקטיבי, קישורים ועוד.
 מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: הפיצוח כולל שתי בעיות גיאומטריות במישור אשר ניתן להכלילן לגיאומטרית המרחב. הבעיה הראשונה מתאימה גם לתלמידי חט"ב ודורשת ידע בחישוב שטחים ונפחי פירמידה. הבעיה השניה דורשת שימוש במשפט פיתגורס ופתרון מערכת משוואות. הבעיות מזמנות חקירה ופיתוח ראיה מרחבית.
 מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
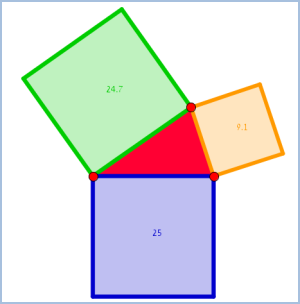
אופי הפעילות: יישום דינאמי בעריכת פרופ' יהודה שוורץ.
לפניכם משולש כלשהו, על צלעותיו בנויים ריבועים. מצאו קשרים שונים בין שטחי הריבועים הללו וקבעו באילו תנאים הם מתקיימים.
 מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
אופי הפעילות: בפעילות יישום דינאמי המציג הוכחה למשפט פיתגורס בעזרת פאזל שיצר פריגל. מומלץ שהתלמידים יגזרוע"פ ההנחיות ויבנו את הפאזל. היישום מדריך כיצד לבנות את הפאזל ומנחה כיצד להוכיח שבניית הפאזל אכן נכונה.
 מקור: מהמרכז הארצי למורים למתמטיקה בחינוך העל יסודי
מקור: מהמרכז הארצי למורים למתמטיקה בחינוך העל יסודי
אופי הפעילות: בפעילות יישום דינאמי המציג הוכחה למשפט פיתגורס בעזרת פאזל. מומלץ שהתלמידים יגזרו ע"פ ההנחיות ויבנו את הפאזל. ביישום הדינאמי ניתן לראות מצבים שונים של בניית הפאזל וכמוכן להמחיש את פתירתו באופן דינאמי. היישום מדריך כיצד לבנות את הפאזל ומנחה כיצד להוכיח שבניית הפאזל אכן נכונה.
 מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
אופי הפעילות: בפיצוח כמה בעיות עתיקות מהודו העוסקות במשפט פיתגורס
 מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
אופי הפעילות: פיצוח המיישם את משפט פיתגורס במרחב.
 מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
אופי הפעילות: בפיצוח מוצגות צורות גאומטריות בעיצוב של פרחים ויש לחשב את שטחן.
 מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
אופי הפעילות: בפיצוח חידות לחישוב שטחים הדורשות יישום של משפט פיתגורס וידע על המעגל.
 מקור: שעשועי מתמטיקה
מקור: שעשועי מתמטיקה
אופי הפעילות: מאמר מבית "אלף אפס" המספר את סיפור מסע היתדות בן ה-3700 שנים על שלשת המספרים הידועה כשלשת פיתגורס. כתבו: זיוה דויטש, עקיבא קדרי.
משפט פיתגורס- מבחר הוכחות ללא מילים, ועוד חידות בנושא.
 מקור: Cut the Knot
מקור: Cut the Knot
אופי הפעילות: 99 הוכחות שונות למשפט פיתגורס, מלוות ביישומים דינאמיים והסברים מפורטים להוכחות.
 מקור: Dan Meyer
מקור: Dan Meyer
אופי הפעילות: סרטון, פעילות חקר.
תאור: פעילות של דן מאייר "מתמטיקה בשלש מערכות". בסרטון נראה שדן בונה שני מיכלים שונים מאותו גודל של נייר ושופך לתוכם פופקורן. מה השאלה העולה בדעתך בהסתכלות בסרטון? במערכה השנייה מעלים את השאלות איזה מידע יש צורך בכדי לפתור את הבעיה? אילו כלים מתמטיים? ופותרים את הבעיה. הפעילות מלווה בסרטונים.

מקור: אתר הפייסבוק של עידן טל
אופי הפעילות: תמונה דינאמית ממחישה ומעוררת דיון כיתתי
תיאור: התמונה הדינאמית מספקת בסיס להוכחה לתכונה של התיכון ליתר במשולש ישר זוית באמצעות הסתכלות על קטע אמצעים במשולש ועל מלבן שחסום בו.
גם אם סדר ההוראה המקובל אינו תואם הוכחה זו, ההקשרים הגיאומטריים המוצגים בתמונה הדינאמית יכולים לעורר מחשבה ודיון משמעותיים.
* אין לשכוח שתמונה דינאמית אינה מספקת הוכחה. יש להשלים הוכחה מדויקת בסיום הדיון שמתקיים בכיתה בעקבות הצפייה בתמונה הדינאמית.
תיאור: אוסף משימות בנושא של סוגי זוויות המכיל פעילויות מיון קצרות המחדדות הבנה. המשימות מתאימות לתלמידי כיתות ח' ברמות השונות ומאפשרות לכל תלמיד בכיתה לענות עליהן בהתאם ליכולותיו.
הפעילות עוסקת בגיאומטריה חישובית בהקשר של ישרים מקבילים וישר חותך, בבעיות אורייניות. המשימות מתאימות לתלמידי כיתות ח' בתחילת השנה.
המשימות כולן כתובות באופן מדורג, בדרגת קושי עולה, כך שכל התלמידים יכולים להתקדם במענה עליהן.
הפעילות מתאימה לשלב בו לומדים גיאומטריה בגישה קדם דדוקטיבית, אך מזמנת דיון גם במושגים כמו משפט ומשפט הפוך, כהכנה לשלב הדדוקטיבי.
תיאור: המשימות בפעילות משלבות בין התחום האלגברי והתחום הגיאומטרי. בתחום האלגברי נדרשות מיומנויות הקשורות לתכונות הפונקציה הקווית ובתחום הגיאומטרי המשימות עוסקות בחפיפת משולשים, דמיון משולשים ותכונות של משולשים שווי שוקיים. השאלות מדורגות כך שבמעבר בין סעיפים יש עליה בדרגת החשיבה הנדרשת לצורך הפתרון. המשימות מתאימות לתלמידי כיתות ח' ברמות הגבוהות אך ניתן לעשות בהן שימוש גם בכיתה ט' כחזרה וריענון על הפרקים שנלמדו בכיתה ח'.
תיאור: הפעילות עוסקת בפונקציות קוויות וצורות גאומטריות שיוצרים הגרפים שלהן במערכת צירים. במסגרת ההוראה של הנושא 'פונקציה קווית' עוסקים בתכונות של הגרפים, כמו מקבילות או חיתוך בין ישרים. בהוראת התחום הגאומטרי עוסקים בחפיפת משולשים, דמיון משולשים, תכונות ומשפטים הקשורים במשולשים שווי שוקיים או משולשים ישרי זווית. השילוב בין התחומים מוצע בפעילות זו באמצעות קישור בין תכונות היסוד של מערכת צירים מאונכת, לבין תכונות גיאומטריות של מרובעים ומשולשים. התלמידים נדרשים להתייחס לתכונות של גרפים, לאפיין באמצעותם מרובעים ומשולשים, למצוא נקודות חיתוך של ישרים, ולחשב אורכים, יחס בין אורכים, שטחים והיקפים. בפעילות נדרש גם שימוש במשפט פיתגורס.
תיאור: הפעילות עוסקת בשילוב בין מיומנויות וידע הקשור בצורות גאומטריות: חפיפה ודמיון משולשים, חישוב שטח, חישוב היקף, חישוב על פי משפט פיתגורס לבין ידע ומיומנויות מהתחום המספרי בהקשר של יחס והסתברות לבין ידע ומיומנויות מהתחום האלגברי בהקשר של הפונקציה הקווית.
תיאור: הפעילות עוסקת בפתרון שאלות תנועה בדרך גרפית תוך שילוב בין הנושאים: פונקציה קווית, יחס, חפיפת משולשים ודמיון משולשים. הפעילות עוסקת בגרפים המתארים מרחק מנקודת יציאה כפונקציה של זמן. בגרפים אלה משמעות השיפוע היא מהירות. כשמדובר בשני גרפים במערכת צירים אחת מבחינים בין מקרים בהם מתוארת יציאה מאותו מקום בהפרש זמנים או יציאה ממקומות שונים באותו זמן או בהפרש זמנים. הפתרונות הנדרשים מבוססים על הבנה ולא על טכניקה אלגברית.
תיאור: אוסף משימות קצרות שמטרתן לחדד, להעמיק את ההבנה ולעורר שיח מתמטי בכיתה. המשימות מתאימות לתלמידי כיתה ט' ברמות הגבוהות. השאלות הן שאלות העמקה בתכונות מרובעים ומשולשים המזמנות פיתוח מיומנויות הוכחה באמצעות המשפטים הנלמדים בתוכנית הלימודים של כיתה ט.
תיאור: אוסף המשימות – שאלות מתפתחות – שלפניכם עוסק בתכונות של מרובעים לכיתה ט' (ללא קטע אמצעים), תכונות של משולש ישר זווית, שטחים של משולשים ומרובעים, שימוש בפרמטרים. הפעילות תומכת בעידוד הוכחה בדרכים שונות, יצירת שיח מתמטי של גילוי ומספקות אפשרות לחזרה מקיפה על כל הנושאים הנ"ל. אוסף המשימות מתאים לרמות הגבוהות, בהתאם לשיקול הדעת של המורה.
תיאור: דף הפעילות עוסק בקשר שבין טענות והיפוכן. הפעילות מזמנת שימוש באלגברה למטרת הוכחה, הן בטענות אלגבריות והן בטענות גאומטריות, וכן חיפוש דוגמאות נגדיות לשם הפרכה. נציין שהפרכה של טענות שגויות באמצעות דוגמאות נגדיות אינו המוקד העיקרי של הפעילות. לנושא של הפרכות תוקדש פעילות אחרת.
תיאור: מטרתה הראשונית של הפעילות "הכל זהב" היא לשמר ידע קודם מלימודי הגאומטריה לקראת נושאים מרכזיים שילמדו בהמשך. כך משלבת הפעילות נושאים בגאומטריה (דמיון משולשים וסכום זוויות במצולע) שהתלמידים רכשו בכיתה ח' ובתחילת כיתה ט' עם תוכן אלגברי ופתרון משוואות ריבועיות הנמצא בלב חומר הלימודים של כיתה ט' כאן גם פוגשים התלמידים משוואה ריבועית שפתרונותיה הם מספרים אי-רציונליים כזריעת זרעים לעתיד.
תיאור: מטרתו של דף העבודה הוא להתנסות ביישום הדרכים השונות להוכיח שמרובע הוא מקבילית. מתאים לבצע את הפעילות בקבוצות במטרה שתלמידים שונים יציעו דרכי פתרון שונות. אחד היתרונות של פתרון בעיה אחת בדרכים שונות (לעומת פתרון של יותר תרגילים, ללא הבקשה למצוא יותר מדרך פתרון אחת), הוא פיתוח גמישות מחשבתית. תלמידים רבים נוטים לאמץ לעצמם דרך הוכחה מועדפת (למשל, חיפוש משולשים חופפים), והם משתמשים בה גם במקרים שקיימת דרך מהירה ופשוטה להוכיח את המבוקש. הדרישה להוכיח טענה בדרכים אחדות מחייבת לסקור דרכי פתרון נוספות, ולחפש תנאים מספיקים מגוונים.
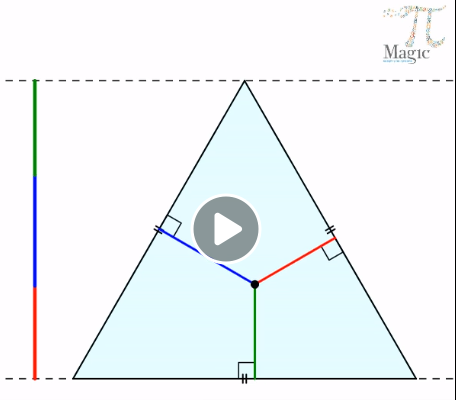
מקור: אתר הפייסבוק של עידן טל
אופי הפעילות: תמונה דינאמית ממחישה ומעוררת דיון כיתתי
תיאור: התמונה ממחישה בתהליך דינאמי את השיוויון של סכום המרחקים של נקודה כלשהי בתוך משולש שווה צלעות מצלעותיו לאורך הגובה של המשולש.
התמונה לא מספקת הוכחה למשפט.
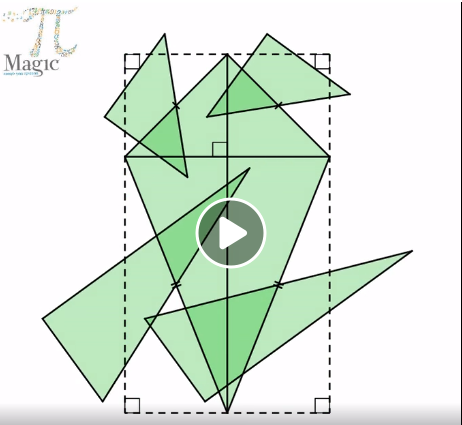
מקור: אתר הפייסבוק של עידן טל
אופי הפעילות: תמונה דינאמית ממחישה ומעוררת דיון כיתתי
תיאור: התמונה ממחישה את הנוסחה לשטח דלתון ע"י "הפיכתו" למלבן ששטחו בדיוק כפליים משטח הדלתון.
ההוכחה נובעת בקלות מהתבוננות בתמונה הדינאמית.
 מקור: מטח
מקור: מטח
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: ביישומון אפשר לבנות מרובעים לפי תכונות אלכסונים שבוחרים מתוך שלושה תפריטים העונים על שלוש שאלות: האם האלכסונים חוצים זה את זה? האם האלכסונים מאונכים זה לזה? האם האלכסונים שווים זה לזה? בחלון המידות יופיעו: בשחור - הנתונים של אלכסוני המרובע שבניתם, בכחול - אורכי הצלעות ומידות הזוויות של המרובע. אפשר לבנות מרובע אחר לפי אותן תכונות של האלכסונים ע"י גרירה של קדקודי המרובע או ע"י לחיצה על בנו מרובע אחר מאותו הסוג.
 מקור: אתר הפייסבוק של עידן טל
מקור: אתר הפייסבוק של עידן טל
אופי הפעילות: תמונה דינאמית ממחישה ומעוררת דיון כיתתי
תיאור: התמונה הדינאמית מציגה דלתונים קעורים וקמורים, מציגה את המעוין כמקרה פרטי של דלתון וממחישה תכונות משותפות לכל הדלתונים.
* אין לשכוח שתמונה דינאמית אינה מספקת הוכחה. יש להשלים הוכחה מדויקת בסיום הדיון שמתקיים בכיתה בעקבות הצפייה בתמונה הדינאמית.
 מקור: מטח
מקור: מטח
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: ביישומון (Applet) משפחת המרובעים אפשר לבנות מרובעים מסוגים שונים על ידי בחירת המרובע הרצוי מתוך תפריט. בחלון המידות יופיעו: סוג המרובע שבחרתם, אורכי הצלעות ומידות הזוויות. אפשר להציג את אלכסוני המרובע, ובחלון המידות יופיעו אורכי האלכסונים והמרחקים מהקדקודים עד נקודת החיתוך של האלכסונים. אפשר לבנות מרובע אחר מאותו הסוג על ידי גרירה של קדקודי המרובע או על ידי לחיצה על בנו מרובע אחר מאותו הסוג.
 מקור: מרכז מורים ארצי למתמטיקה בחינוך העל יסודי
מקור: מרכז מורים ארצי למתמטיקה בחינוך העל יסודי
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: דף עבודה ויישום דינאמי לחקירת תכונות האלכסונים בטרפז. בדף העבודה הנחיות לחקירה והוכחה של המשפט: הקו המקביל לאלכסוני הטרפז ועובר דרך נקודת מפגש האלכסונים שווה לממוצע ההרמוני של הבסיסים.
 מקור: מרכז מורים ארצי למתמטיקה בחינוך העל יסודי
מקור: מרכז מורים ארצי למתמטיקה בחינוך העל יסודי
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: דף עבודה ויישום דינאמי בהם מוצגים שישה ריבועים, אך עם גרירת הקודקודים הם משתנים. המשימה לזהות כיצד נבנה כל מרובע ולאפיין אותו. מה מיוחד בריבוע?
 מקור: המרכז הארצי למתמטיקה בחינוך העל יסודי
מקור: המרכז הארצי למתמטיקה בחינוך העל יסודי
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: יישום דינאמי בו יש להוכיח כי קיים מלבן ששטחו שווה לשטח המקבילית . או במילים אחרות המחשה לכך ששטח כל המקביליות עם צלע נתונה (a) וגובה נתון (h) שווה, והוא שווה לשטח המלבן שאורך צלעותיו כצלע המקבילית והגובה.
 מקור: המרכז הארצי למתמטיקה בחינוך העל יסודי
מקור: המרכז הארצי למתמטיקה בחינוך העל יסודי
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: דף עבודה אינטראקטיבי ויישום דינאמי בגאוגברה לחקר בעיה בגיאומטריה. הבעיה עוסקת בתכונות המלבן ושטח משולש.
 מקור: מתמטיקה משולבת, מכון וייצמן
מקור: מתמטיקה משולבת, מכון וייצמן
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: דף עבודה אינטראקטיבי בגאוגברה לחקירה של בעיה בגיאומטריה. בהינתן מרובע כלשהו נעביר דרך קודקודיו מקבילים לאלכסוניו. איזה מרובע נקבל? בדף העבודה הנחיות לחקירה של מצבים שונים ובחינת התכונות של משפחת המרובעים.
 מקור: המרכז הארצי למתמטיקה בחינוך העל יסודי
מקור: המרכז הארצי למתמטיקה בחינוך העל יסודי
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: דף עבודה אינטראקטיבי ויישום דינאמי בגאוגברה לחקר בעיה בגיאומטריה. בהינתן מרובע כלשהו, ניצור מרובע פנימי ששניים מקודקודיו על אמצעי האלכסונים והשניים האחרים על אמצעי צלעות מנוגדות של המרובע. בדף העבודה הנחיות לבנייה בגאוגברה. מבוסס על בחינת בגרות: שאלון 804, קיץ תשע"ב, שאלה 4 .
 מקור: מתמטיקה משולבת, מכון וייצמן
מקור: מתמטיקה משולבת, מכון וייצמן
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: דף עבודה אינטראקטיבי בגאוגברה לחקירה של בעיה בגיאומטריה. בהינתן מרובע כלשהו איזה מרובע נקבל אם נחבר את אמצעי צלעותיו? איזה מרובע פנימי נקבל ממלבן. ולהיפך, מאיזה מרובע חיצוני נקבל מרובע פנימי מלבן? מה הקשר בין השטחים? מה עוד ניתן לשאול? מקור: מתמטיקה משולבת, מכון וייצמן.
 מקור: המרכז הארצי למתמטיקה בחינוך העל יסודי
מקור: המרכז הארצי למתמטיקה בחינוך העל יסודי
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: פיצוח העוסק בתכונות מרובעים שאלכסוניהם מאונכים. בשאלה הראשונה חוקרים את המרובעים השונים ואת שטחיהם, תוך קיפולי נייר ושימוש ביישום דינאמי. בבעייה השנייה מחפשים מעוין החסום במלבן. בעיה זו דורשת הכרות עם תכונות המרובעים ובפרט המעוין וכן שימוש במשפט פיתגורס ובאלגברה.
 מקור: Maths is Fun
מקור: Maths is Fun
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: כלי אינטראקטיבי המציג את סוגי המרובעים השונים ואת תכונותיהם. ניתן לשנות את מימדי כל מרובע ולחקור מה משתנה ומה נשאר קבוע.
 מקור: illuminations
מקור: illuminations
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: הדגמה אינטראקטיבית כיצד ניתן לחלק את המקבילית לשני שטחים וליצור ממנה מלבן ועל ידי כך לפתח את הנוסחה לשטח מקבילית ובכל לגלות את נוסחת השטח של מקבילית.
 מקור: illuminations
מקור: illuminations
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: אלכסוני המרובע יכולים להיחתך באופנים שונים: הם יכולים להיות מאונכים זה לזה, הם יכולים להיות שווים או לא, אחד מהם עשוי לחצות את השני, או ששניהם חוצים זה את זה. בפעילות זו חוקרים אילו סוגים של מרובעים ניתן ליצור על פי תכונות נתונות של האלכסונים. מלווה בתכנון שיעור ובדפי עבודה (אנגלית).
 מקור: illuminations
מקור: illuminations
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: יישום דינאמי לחקירת השטחים של משולש ושל טרפז ומקבילית. בכלי ניתן לאסוף ממצאים של אורכי הצלעות והגבהים ולמצוא את הקשר שלהם לנוסחת השטח. נשאלת השאלה נה הדומה ומה השונה בין נוסחאות השטח השונות.
 מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי.
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי.
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: בפיצוח בעיות למציאת שטחים של מרובעים ומשולשים.
 מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: הפיצוח כולל אוסף בעיות לחישוב שטחים החסומים באופנים שונים בתוך ריבוע. הבעיות מזמנות חקירה וחשיבה יצירתית.
 מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: משחק אינטראקטיבי לזיהוי של ריבועים בתוך רשת קורדינטות . מלווה בפיצוח.
 מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: הפיצוח כולל שתי בעיות גיאומטריות במישור אשר ניתן להכלילן לגיאומטרית המרחב. הבעיה הראשונה מתאימה גם לתלמידי חט"ב ודורשת ידע בחישוב שטחים ונפחי פירמידה. הבעיה השניה דורשת שימוש במשפט פיתגורס ופתרון מערכת משוואות. הבעיות מזמנות חקירה ופיתוח ראיה מרחבית.
תיאור: אוסף משימות קצרות שמטרתן לחדד, להעמיק את ההבנה ולעורר שיח מתמטי בכיתה. המשימות מתאימות לתלמידי כיתה ט' ברמות הגבוהות. השאלות הן שאלות העמקה בתכונות מרובעים ומשולשים המזמנות פיתוח מיומנויות הוכחה באמצעות המשפטים הנלמדים בתוכנית הלימודים של כיתה ט.
תיאור: דף הפעילות עוסק בקשר שבין טענות והיפוכן. הפעילות מזמנת שימוש באלגברה למטרת הוכחה, הן בטענות אלגבריות והן בטענות גאומטריות, וכן חיפוש דוגמאות נגדיות לשם הפרכה. נציין שהפרכה של טענות שגויות באמצעות דוגמאות נגדיות אינו המוקד העיקרי של הפעילות. לנושא של הפרכות תוקדש פעילות אחרת.
תיאור: מטרתה הראשונית של הפעילות "הכל זהב" היא לשמר ידע קודם מלימודי הגאומטריה לקראת נושאים מרכזיים שילמדו בהמשך. כך משלבת הפעילות נושאים בגאומטריה (דמיון משולשים וסכום זוויות במצולע) שהתלמידים רכשו בכיתה ח' ובתחילת כיתה ט' עם תוכן אלגברי ופתרון משוואות ריבועיות הנמצא בלב חומר הלימודים של כיתה ט' כאן גם פוגשים התלמידים משוואה ריבועית שפתרונותיה הם מספרים אי-רציונליים כזריעת זרעים לעתיד.
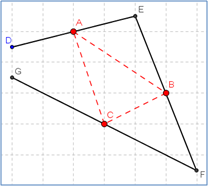 מקור: מרכז מורים ארצי למתמטיקה בחינוך העל יסודי
מקור: מרכז מורים ארצי למתמטיקה בחינוך העל יסודי
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: דף עבודה, יישום דינאמי - משולש לבעית חקר האם וכיצד ניתן לבנות משולש מנקודות אמצעי הצלעות. הבעיה גם מורחבת למרובעים וניתן לחקור בעזרתה יישום דינאמי - מרובע
 מקור: אתר הפייסבוק של עידן טל
מקור: אתר הפייסבוק של עידן טל
אופי הפעילות: תמונה דינאמית ממחישה ומעוררת דיון כיתתי
תיאור: התמונה הדינאמית מספקת בסיס להוכחה לתכונה של התיכון ליתר במשולש ישר זוית באמצעות הסתכלות על קטע אמצעים במשולש ועל מלבן שחסום בו.
גם אם סדר ההוראה המקובל אינו תואם הוכחה זו, ההקשרים הגיאומטריים המוצגים בתמונה הדינאמית יכולים לעורר מחשבה ודיון משמעותיים.
* אין לשכוח שתמונה דינאמית אינה מספקת הוכחה. יש להשלים הוכחה מדויקת בסיום הדיון שמתקיים בכיתה בעקבות הצפייה בתמונה הדינאמית.

מקור: אתר הפייסבוק של עידן טל
אופי הפעילות: תמונה דינאמית ממחישה ומעוררת דיון כיתתי
תיאור: התמונה ממחישה בתהליך דינאמי את השיוויון של סכום המרחקים של נקודה כלשהי בתוך משולש שווה צלעות מצלעותיו לאורך הגובה של המשולש.
התמונה לא מספקת הוכחה למשפט.
מקור: אתר הפייסבוק של עידן טל
אופי הפעילות: תמונה דינאמית ממחישה ומעוררת דיון כיתתי
תיאור: בתמונה הדינאמית מחולק משולש לארבעה משלושים חופפים, כך שניתן להסיק את תכונת קטע האמצעים. עוד ניתן לדבר על חפיפת משולשים, דמיון משולשים ומושגים קשורים.
* אין לשכוח שתמונה דינאמית אינה מספקת הוכחה. יש להשלים הוכחה מדויקת בסיום הדיון שמתקיים בכיתה בעקבות הצפייה בתמונה הדינאמית.
 מקור: מרכז מורים ארצי למתמטיקה בחינוך העל יסודי
מקור: מרכז מורים ארצי למתמטיקה בחינוך העל יסודי
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: דף עבודה אינטראקטיבי ויישום דינאמי לדיון וחקירה של המשפט: הגובה במשולש ישר זווית שווה לממוצע הגיאומטרי של היטליו.
קישור ל בניית מגן דוד בתוכנת compass
קישור לסרטוני הדרכה
קישור למדור "כיתה מדעית"
אופי הפעילות: יישום דינאמי בו ניתן לבנות מבנים מקוביות על פי דגם , או בניה חופשית, ולראות אותו ממבטים שונים.
תיאור: היישומון בהפקת אלנט עבור אגף טכנולוגיות מידע במשרד החינוך.
 מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
אופי הפעילות: סרטון בתלת מימד ויישומון (דרוש להוריד גאוגברה 5)
תאור: מתבסס על שאלה מתוך דוגמאות למבחני פיזה 2012.
בסרטון ניתן להתבונן במחסן במבטים שונים. ביישומון נבנה המחסן על פי התוכנית המתוארת בשאלה וניתן להתבונן בו בתצוגת תלת מימד, לסובב ואף לשנות את מימדי המחסן. ניתן גם ליצור מבט על, צד קדמי אחורי וכדומה.
* יש צורך להוריד את גרסת הניסוי של גאוגברה 5.
תיאור: אוסף משימות קצרות שמטרתן לחדד, להעמיק את ההבנה ולעורר שיח מתמטי בכיתה. המשימות מתאימות לתלמידי כיתה ט' ברמות הגבוהות. השאלות מתייחסות לצורות גיאומטריות בתוך מערכת צירים. השאלות משלבות בין מיומנויות של הבנת מיקומים במערכת צירים, מיומנויות אלגבריות הקשורות בפונקציות קוויות וידע והבנה באשר לתכונות הגיאומטריות של משולשים ומרובעים.
תיאור: הפעילות עוסקת בנושאים אחדים שיש להם חשיבות מרכזית בתכנית הלימודים של כיתה י: גאומטריה אנליטית, דמיון משולשים והזזות.
הפעילות מאפשרת לערוך חזרה על הפונקציה הקווית ועל ישרים במערכת צירים (גם כאלה שאינם גרפים של פונקציות) בהקשר טבעי של שיעורי הגאומטריה, ולהדגיש את הקשר בין פתרון משוואות ונקודות במערכת צירים.
בשאלות אחדות בפעילות זו משולבים ישרים המקבילים לצירים. אחת הסיבות היא שבאופן כזה יצרנו בקלות משולשים ישרי זווית ולכן ניתן לחשב בקלות אורכי קטעים באמצעות משפט פיתגורס, מבלי להזדקק לנוסחת המרחק בין נקודות. כאשר, בשנים הבאות, התלמידים יפגשו את נוסחת המרחק, הנוסחה תהיה עבורם ביטוי אלגברי לפעולה שהם מכירים.
תיאור: הפעילות עוסקת בנושאים אחדים שיש להם חשיבות מרכזית בתכנית הלימודים של כיתה י': גאומטריה אנליטית, דמיון משולשים והזזות.
הפעילות מאפשרת לערוך חזרה על הפונקציה הקווית ועל ישרים במערכת צירים (גם כאלה שאינם גרפים של פונקציות) בהקשר טבעי של שיעורי הגאומטריה, ולהדגיש את הקשר בין פתרון משוואות ונקודות במערכת צירים.
 מקור: מחונNet
מקור: מחונNet
אופי הפעילות: חקרשת שנפתח בסיפור על ההראג'ה ההודי והפיל החולה שלו וממשיך בלימוד עצמי של נושא החזקות ומשימות שונות בקבוצות.
 מקור: Cary and Michael Huang
מקור: Cary and Michael Huang
אופי הפעילות: תוכנה ידידותית וויזואלית להתרשמות מסדרי גודל בעולם. מה הגודל של חיידקים? ומה הגודל של היקום? התוכנה מציגה בשפות שונות, גם בעברית,סרגל שניתן לנוע עליו, ומראה גופים בגדלים שונים,
מהחלקיקים הקטנים ביותר ועד לגלקסיות עצומות. ראו הצעה לפעילות באתר כיתה בפיתה.
 מקור: Office of Charles and Roy Eames
מקור: Office of Charles and Roy Eames
אופי הפעילות: סרטון מרהיב
תאור: תרגיל קולנועי מדעי, בקריינתו של פיל מוריסון. סדרת תמונות של זוג עורך פיקניק בפארק, בה כל תמונה מראה אזור קטן פי עשרה מהקודמת. הסדרה מתחילה בתמונה של היקום המוכר כולו, והמצלמה מתמקדת בהדרגה, עד שניתן לראות את החלקיקיים התת-אטומיים בתוך ידו של הגבר.
 מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
אופי הפעילות: הפיצוח עוסק בחקירת תהליכי גידול מעריכי. ניתן לשלב בלימוד סדרה הנדסית או בבעיות גדול ודעיכה.
 מקור: הילקוט הדיגיטלי של מטח לחט"ב
מקור: הילקוט הדיגיטלי של מטח לחט"ב
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: בפעילות מופיעים תרגילים העוסקים בסדר פעולות חשבון במספרים טבעיים. בפעילות יש 3 סעיפים: תרגילים עם שתי פעולות ובלי סוגריים, תרגילים עם שתי פעולות וסוגריים, ותרגילים עם שלוש פעולות. כמו כן ניתן למצוא פעילויות משחק נוספות בנושא כגון: התרגילון: סדר פעולות - הוסיפו פעולות וסוגריים התרגילון: סדר פעולות במספרים עשרוניים, התרגילון: סדר פעולות - חידות.
 מקור: הטלויזיה החינוכית
מקור: הטלויזיה החינוכית
אופי הפעילות: משדר נוסטלגי של הטלויזיה הלימודית המציג את המספרים המכוונים, בניית ציר המספרים ועיסוק בסדר בין המספרים. מלווה באנימציות ובהמחשות כולל טיול למקום הנמוך ביותר בעולם.
 מקור: nrich
מקור: nrich
אופי הפעילות: משחק מאתגר המשלב אסטרטגיה ותרגול חיבור וחיסור של מספרים שליליים. הגרילו שני מספרים בקובייה. חברו תרגיל שתוצאתו על הלוח ונסו ליצור רצף של שלושה מספרים בלוח. ניתן לשחק עם חבר או נגד המחשב, וכן לקבוע את רמת המשחק.
 מקור: BBC
מקור: BBC
אופי הפעילות: שלושה משחקי הרפתקה משולבים בוידאו. הילחמו ברובוטים המנסים להשתלט בעולם, פתרו משימות בסדר המספרים השליליים והצילו את העולם....
 מקור: WHY U, תרגום דוידסון און-ליין
מקור: WHY U, תרגום דוידסון און-ליין
אופי הפעילות: סרטון אנימציה המציג הסברים לפעולת הכפל בין מספרים שליליים. הסרטון הוא השמיני בסדרה , המציגה נושאים שונים בתחום הטרום אלגברה. (בתרגום של מכון דוידסון). בפרק זה נבדוק ביחד עם פרופסור ון שמוהוק מה הם חוקי הכפל כאשר אחד או יותר מהאופרנדים המוכפלים הוא שלילי, ומה עומד מאחורי החוקים האלה.
 מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
אופי הפעילות: יישום דינאמי בגאוגברה, בו ניתן להדגים ולחקור סכום של מספרים שליליים.
במודל זה כל רישום מספרי מתואר על-ידי חץ (וקטור) שלו גודל וכוון. כאשר אורך החץ מבטא את ערכו המוחלט של המספר וכיוונו מבטא את סימנו:
חץ ימינה מספר חיובי, חץ שמאלה מספר שלילי. מכאן גם השם מספרים מכוונים.
 מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
אופי הפעילות: יישום דינאמי בגאוגברה, בו ניתן להדגים ולחקור סכום של מספרים שליליים במודל הקשתות. המחובר הראשון מוצג כנקודה על ציר המספרים והמחובר השני מייצג תנועה בצעדים ימינה או שמאלה- תלוי בסימן המחובר השני. תנועה ימינה- המחובר השני חיובי ותנועה שמאלה- המחובר השני שלילי. תוצאת החיבור היא הנקודה אליה הגענו.
 מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
אופי הפעילות: הפיצוח "בארץ יצורי הפרא המתמטיים" עוסק בפעולות החיבור והחיסור של מספרים שליליים באמצעות מודל אסימונים, בו מספר חיובי מיוצג ע" אסימון כחול ומספר שלילי ע"י אסימון אדום ושניהם יחד מהווים את זוג האפס. הפיצוח ערוך כדפי עבודה לתלמיד ומלווה בסרטונים קצרים ובמשחקים אינטראקטיביים לתרגול פעולות החיבור והחיסור. כמו כן, תמצאו סקירה קצרה על ההיסטוריה של המספרים השליליים, משחקים ומקורות מגוונים בנושא. שימו לב בפרט ליחידת השתלמות מורים המציגה את המודל על יתרונותיו וחסרונותיו.
אופי הפעילות: סרטון אינטראקטיבי וגרסת הסרטון
תיאור: סרטון אינטראקטיבי בנושא יחס פרי יצירתו של עמרי נווה. הסרטון מציג סיפור מסיבת יומולדת ובו משולבות בעיות שונות והסבר בהיר לפתרונן וכולן בנושא היחס.
 מקור: משימות אוריינות, עקרון המנוף
מקור: משימות אוריינות, עקרון המנוף
אופי הפעילות: מצגת ויישום דינאמי
תיאור: מצגת המציעה פעילות המלווה את המשימה האוריינית "עקרון המנוף" המציג בעיה של שינוי יחס בשיווי משקל בנדנדה. הפעילות מציעה חקר וגילוי של עקרון המנוף בעזרת מאזני מספרים. יישומון המנוף בהפקת אלנט עבור אגף טכנולוגיות מידע במשרד החינוך.
 מקור: שאלות לדוגמא ממבחן פיזה
מקור: שאלות לדוגמא ממבחן פיזה
אופי הפעילות: המרכז הישראלי למצויינות בחינוך עבור אגף טכנולוגיות מידע במשרד החינוך.
תיאור: יישומון המציע חקירה של אומדן שטחים וקנה מידה של שטחים כלשהם, כגון כתם הנפט שבמשימת האוריינות שמבחני פיזה. ביישומון ניתן לשנות את קנה המידה, ליצור שטחים שונים, גם על פי תמונה, ולאמוד את שטחם. היישומון מלווה בסרטון הסבר.

יישומונים: המרכז הישראלי למצויינות בחינוך עבור אגף טכנולוגיות מידע במשרד החינוך.
אופי הפעילות: סרטון ויישומון .
תיאור: יישומון המציע חקירה של בעיות שונות של חישובי הנחות באחוזים, והשוואה בין מבצעים שונים. ביישומון מודל ויזואלי פשוט לחשוב אחוזים מכמות. היישומון מלווה בסרטון הסבר. בסרטון הצעה כיצד ניתן להכליל שאלות מסוג זה ולפתור אותן אלגברית.
מקור: MEI
משחקון אינטראקטיבי למחשב או לנייד בו יש להעריך את הממוצע והחציון בגרף עמודות.
המשחק הוא עם ניקוד ועל זמן.
 מקור: gapminder
מקור: gapminder
תאור: תוכנה סטטיסטית הממירה נתונים ממקורות בינלאומיים שונים לגרפים ויזואליים, דינאמיים ואינטראקטיביים המסייעים לפישוט והבנת תהליכים מורכבים. כלי זה התפרסם ברבים אחרי שהמפתח הראשי שלו Hans Rosling נתן הרצאה באירוע המרכזי של 2007 Ted וקיבל את הכותרת החצי רשמית The best stats you've ever seen. הכלי שרוסלינג פיתח נרכש על ידי חברת Google וכיום אפשר להציג ולהצליב בעזרתו נתונים ממאגרים שונים. באתר סרטונים רבים, גרפים דינאמיים מוכנים ומדריכים למורה. לדוגמה הגרף הדינאמי: האם יש קשר בין שכר לבריאות? בו תוכלו לשנות פרמטרים שונים, ייצוגים גרפיים שונים ולעקוב אחר המגמות.
 מקור: gapminder
מקור: gapminder
אופי הפעילות: סרטון הדרכה
תאור:סרטון באורך 4 דקות בנושא סטטיסטיקה וייצוגים שונים של נתונים. הצצה לתוכנה הסטטיסטית והחינמית GAPMINDER. בסרטון יש ניתוח מרתק כיצד השתנו המגמות בעולם של אורך החיים בארצות שונות כתלות בהכנסה, לאורך 200 השנים האחרונות. הייצוג הגרפי מעניין ולא שגרתי: כל בועה מייצגת מדינה וגודל הבועה מייצג את גודל האוכלוסין בה, צבע הבועה מייצג את היבשת.
.הסרטון מלווה במדריך למורה ובסדרת סרטונים נוספת בנושא, המשלבים נושאים כלכליים וחברתיים וסטטיסטיקה.
 מקור: מטח
מקור: מטח
אופי הפעילות: גליונות מתמטיים
תאור: גם - גיליונות מתמטיים הוא פרויקט הכולל אוסף של פעילויות חקר בנושאים שונים במתמטיקה. חלק מהפעילויות נמצאות באתר. כל פעילות היא חוברת עבודה ב- Excel מבנה הפעילויות הוא מדורג, כך שכל תלמיד יכול להתקדם בקצב אישי. עם זאת הפעילויות מעודדות שיתוף פעולה בין התלמידים לבין עצמם ובין התלמידים לבין מנחה הפעילות. האתר משמש במה לדיונים שיתעוררו במהלך ביצוע הפעילויות, והוא פתוח לתלמידים ולמורים. האתר כולל מאגר משימות, פורום מורים, פורום תלמידים וכן "טיפים" הקשורים לעבודה עם ה-Excel.
 מקור: TED
מקור: TED
אופי הפעילות: הרצאה
תאור: הרצאה מבית TED – 3 דקות - הצעה נועזת ללמד כמקצוע ראשי במתמטיקה סטטיסטיקה ולאו דוקא אלגברה, פונקציות וחדו"א. דיון – מה דעתכם על ההצעה המהפכנית? מה מקומה של הסטטיסטיקה בתרבות המודרנית? מה מקומה בתוכנית הלימודים? כיצד נוכל לתת לה את המקום המכובד שמגיע לה?
 מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
אופי הפעילות: הפיצוח בנושא הסתברות כולל יישום אינטראקטיבי (מתוך NRICH) של גלגלי מזל שונים (רולטה) .בפיצוח מספר פעילויות לחקירת ההסתברות של אירועים דו שלביים ויותר. בפיצוח חקירה של הקשר בין הסתברות ניסויית, בה חוזרים שוב ושוב על הניסוי ויוצרים טבלת שכיחויות וגרף עמודות, לבין הסתברות תיאורטית.
 מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
אופי הפעילות: בפיצוח בעיות ברמות קושי שונות בהסתברות. בבעייה הראשונה משחק בו ניתן להתנסות עם יישום אינטראקטיבי.
 מקור:
מקור:
אופי הפעילות: מטבע, קובייה, קלפים וגלגלי מזל - אוסף כלים אינטראקטיביים להגרלה. ניתן לבצע את ניסוי ההגרלה שוב ושוב ולראות את ההתאמה בין ההסתברות הניסויית להסתברות התיאורטית.
כלי אינטראקטיבי לבניית גלגל מזל צבעוני
Virtual Spinner - גלגל מזל אינטראקטיבי – יישומון בו ניתן לעצב את גלגל המזל ולהגריל מספר.
Virtual Dice – קובייה אינטראקטיבית - יישומון בו ניתן לבחור מספר קוביות ולהגריל מספרים
 מקור: Math Interactivities
מקור: Math Interactivities
אופי הפעילות: שחקו בסולמות ונחשים, משחק אינטראקטיבי, עם גלגלי מזל (רמה 1) או שתי קוביות (רמה 2) וחקרו מה ההסתברות שלכם לטפס במעלה הלוח. הפעילות כוללת גם דפי עבודה, פתרונות ולוח משחק להדפסה.
 מקור: mrnussbaum
מקור: mrnussbaum
אופי הפעילות: משחק אינטרנטי (מותאם גם ל-IPAD) בו מספר שלבים. המטרה לזכות בכמה שיותר כרטיסים במשחקים בהם יש לחשב הסתברויות ברמות שונות. הכרטיסים יזכו אותך בכניסה ליריד בו עוד חמישה משחקי הסתברות שונים
 מקור: learnalberta
מקור: learnalberta
אופי הפעילות: סרטון ופעילות אינטראקטיבית לחקר ההבדל בין הסתברות ניסויית והסתברות תיאורטית והצגתן בגרף עמודות או טבלת שכיחות יחסית. מלווה בדף עבודה.
 מקור: TeachingWithVideo's channel
מקור: TeachingWithVideo's channel
אופי הפעילות: סרטון אנימציה משעשע, תלת מימד, המסביר בפשטות והומור מושגי יסוד בהסתברות
תיאור: הפעילות עוסקת בשילוב בין מיומנויות וידע הקשור בצורות גאומטריות: חפיפה ודמיון משולשים, חישוב שטח, חישוב היקף, חישוב על פי משפט פיתגורס לבין ידע ומיומנויות מהתחום המספרי בהקשר של יחס והסתברות לבין ידע ומיומנויות מהתחום האלגברי בהקשר של הפונקציה הקווית.
תיאור: הפעילויות בדף שלפנינו נוגעות כולן בפעולות חישוביות ואלגבריות המשלבות שורשים.
המטרה היא לחזק את המיומנויות האלגבריות בחיבור וחיסור עם שורשים כמו גם כפל וחילוק עם שורשים. כחלק מהתרגול יש שימוש במשפט פיתגורס, בדמיון ובנוסחאות הכפל המקוצר.
בפעילויות השונות מתנסים בהכפלת מספר או ביטוי עם שורש בביטוי אחר בכדי לקבל מספר ללא שורש.

תיאור: סרטון המלווה גם בשיעור מבית היוצר של Ted-Ed. לרובנו יש קושי לדמיין מספרים גדולים מאד או קטנים מאד. בסרטון האנימציה יש מספר המחשות לכמה זה אחד חלקי מיליון.
 מקור: math-play.com, onlinemathlearning.com and kahanacademy.org
מקור: math-play.com, onlinemathlearning.com and kahanacademy.org
אופי הפעילות: משחק לתרגול חוקי החזקות עם KIWI
תרגול אינטראקטיבי של חוקי החזקות באוניברסיטת קאהן.
מקור:  Office of Charles and Roy Eames
Office of Charles and Roy Eames
אופי הפעילות: סרטון מרהיב
תאור: תרגיל קולנועי מדעי, בקריינתו של פיל מוריסון. סדרת תמונות של זוג עורך פיקניק בפארק, בה כל תמונה מראה אזור קטן פי עשרה מהקודמת. הסדרה מתחילה בתמונה של היקום המוכר כולו, והמצלמה מתמקדת בהדרגה, עד שניתן לראות את החלקיקיים התת-אטומיים בתוך ידו של הגבר.
 מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
אופי הפעילות: הפיצוח עוסק בחקירת תהליכי גידול מעריכי. ניתן לשלב בלימוד סדרה הנדסית או בבעיות גדול ודעיכה.
 מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
אופי הפעילות: פיצוח הכולל חידות המסודרות מן הקל אל הכבד. פתרון החידות דורש ידע בחוקי חזקות ובחשבון מודולארי (שאריות). תוכלו לשלב את החידות בהוראת נושא החזקות, בהעשרה ואפילו בנושא האינדוקציה בו נראה שיטות הוכחה שונות לבעיות של חלוקה במספר.
 מקור: htwins.net
מקור: htwins.net
אופי הפעילות: תוכנה ידידותית וויזואלית להתרשמות מסדרי גודל בעולם. מה הגודל של חיידקים? ומה הגודל של היקום? התוכנה מציגה בשפות שונות, גם בעברית,סרגל שניתן לנוע עליו, ומראה גופים בגדלים שונים, מהחלקיקים הקטנים ביותר ועד לגלקסיות עצומות.
ראו הצעה לפעילות באתר כיתה בפיתה.
תיאור: הפעילויות בדף שלפנינו נוגעות כולן בפעולות חישוביות ואלגבריות המשלבות שורשים.
המטרה היא לחזק את המיומנויות האלגבריות בחיבור וחיסור עם שורשים כמו גם כפל וחילוק עם שורשים. כחלק מהתרגול יש שימוש במשפט פיתגורס, בדמיון ובנוסחאות הכפל המקוצר.
בפעילויות השונות מתנסים בהכפלת מספר או ביטוי עם שורש בביטוי אחר בכדי לקבל מספר ללא שורש.
 מקור: NGFL-cymru
מקור: NGFL-cymru
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: משחק זכרון אינטרנטי, התאמה של זוגות ביטויים מספריים עם שורש.
 מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
אופי הפעילות: הפיצוח עוסק בהסתברות ומעט בסטטיסטיקה. בפיצוח פעילות לחקר התפלגות בינומית תוך ניסוי בסימולציה דינאמית של לוח גלטון (הדומה למשולש פסקל). התלמידים חוקרים את גרף הפעמון, העקומה הנורמלית ומפתחים את הנוסחאות להסתברות בינומית, תוך שימוש במשולש פסקל. בפיצוח הפניות לרקע הסטורי של ענף ההסתברות ושימושים בתרבות המודרנית (חכמת ההמונים).
אופי הפעילות: מטבע, קובייה, קלפים וגלגלי מזל - אוסף כלים אינטראקטיביים להגרלה. ניתן לבצע את ניסוי ההגרלה שוב ושוב ולראות את ההתאמה בין ההסתברות הניסויית להסתברות התיאורטית.
כלי אינטראקטיבי לבניית גלגל מזל צבעוני
Virtual Spinner - גלגל מזל אינטראקטיבי – יישומון בו ניתן לעצב את גלגל המזל ולהגריל מספר.
Virtual Dice – קובייה אינטראקטיבית - יישומון בו ניתן לבחור מספר קוביות ולהגריל מספרים
 מקור: Math Interactivities
מקור: Math Interactivities
אופי הפעילות: שחקו בסולמות ונחשים, משחק אינטראקטיבי, עם גלגלי מזל (רמה 1) או שתי קוביות (רמה 2) וחקרו מה ההסתברות שלכם לטפס במעלה הלוח. הפעילות כוללת גם דפי עבודה, פתרונות ולוח משחק להדפסה.
 מקור: mrnussbaum
מקור: mrnussbaum
אופי הפעילות: משחק אינטרנטי (מותאם גם ל-IPAD) בו מספר שלבים. המטרה לזכות בכמה שיותר כרטיסים במשחקים בהם יש לחשב הסתברויות ברמות שונות. הכרטיסים יזכו אותך בכניסה ליריד בו עוד חמישה משחקי הסתברות שונים.
 מקור: Math Interactives
מקור: Math Interactives
אופי הפעילות: סרטון ופעילות אינטראקטיבית לחקר ההבדל בין הסתברות ניסויית והסתברות תיאורטית והצגתן בגרף עמודות או טבלת שכיחות יחסית. מלווה בדף עבודה.
 מקור: TeachingWithVideo's
מקור: TeachingWithVideo's
אופי הפעילות: סרטון אנימציה משעשע, תלת מימד, המסביר בפשטות והומור מושגי יסוד בהסתברות.
 מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
אופי הפעילות: הפיצוח בנושא הסתברות כולל יישום אינטראקטיבי (מתוך NRICH) של גלגלי מזל שונים (רולטה) .בפיצוח מספר פעילויות לחקירת ההסתברות של אירועים דו שלביים ויותר. בפיצוח חקירה של הקשר בין הסתברות ניסויית, בה חוזרים שוב ושוב על הניסוי ויוצרים טבלת שכיחויות וגרף עמודות, לבין הסתברות תיאורטית.
 מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
אופי הפעילות: בפיצוח בעיות ברמות קושי שונות בהסתברות. בבעייה הראשונה משחק בו ניתן להתנסות עם יישום אינטראקטיבי.





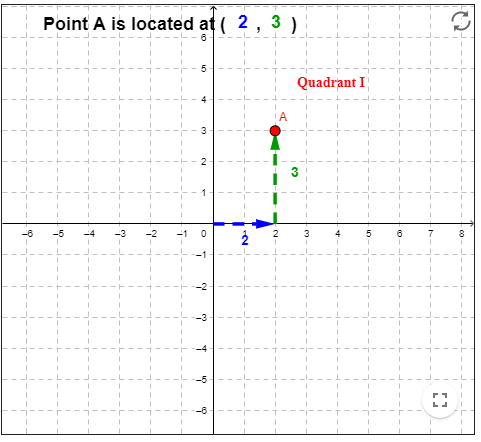



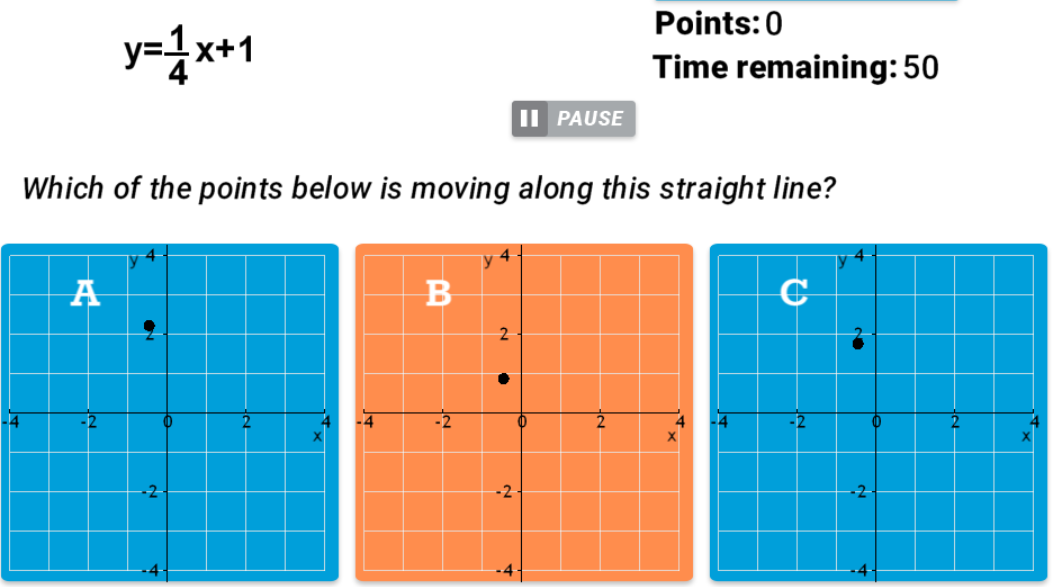


 מקור:
מקור: 
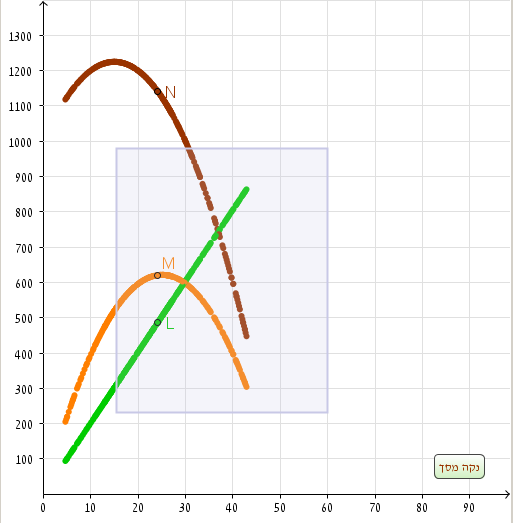 מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי


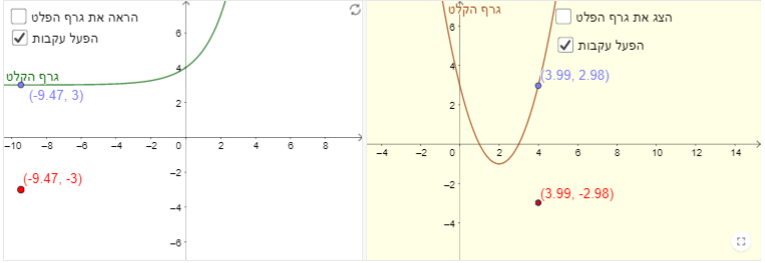

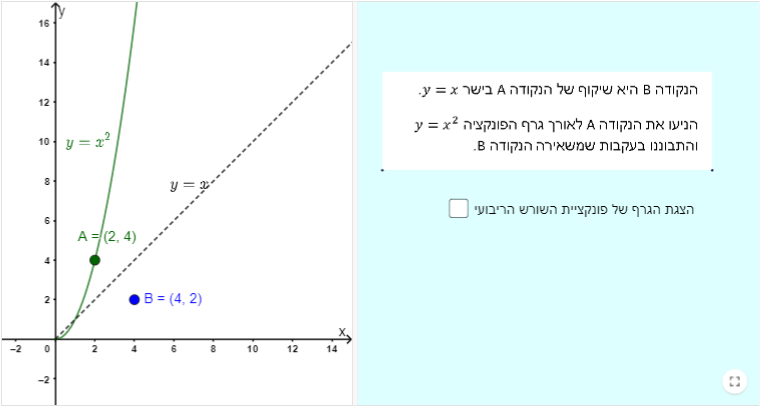
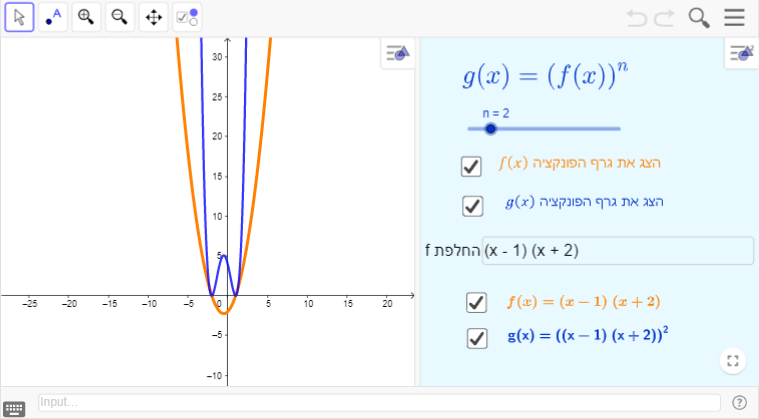


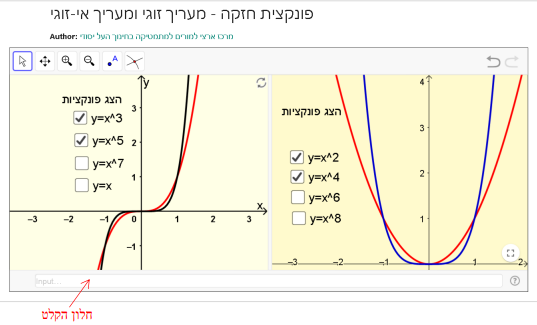



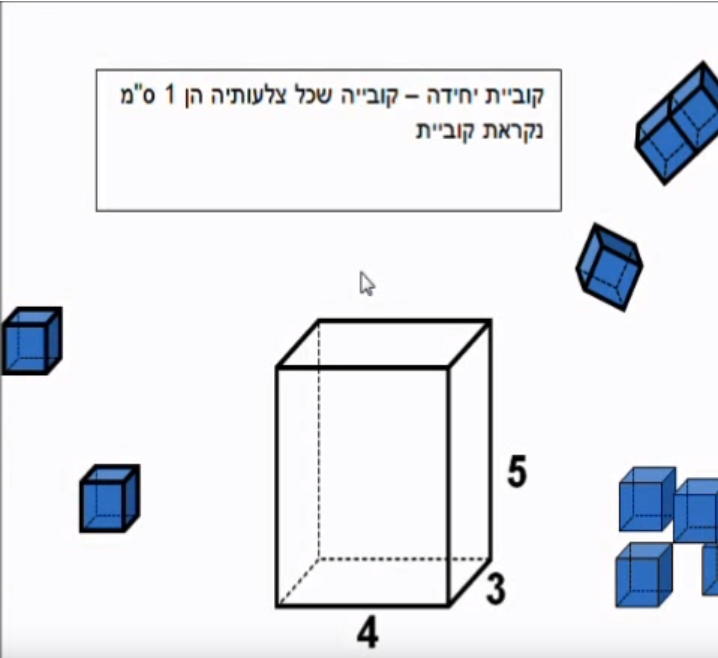





 מקור:
מקור: 
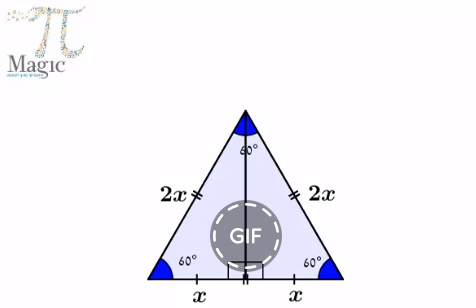 מקור:
מקור: