המרכז הארצי למורים למתמטיקה בחינוך העל יסודי

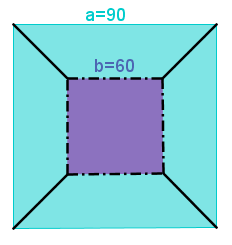
1. ללא מילים

לפניכם שלוש הוכחות דינאמיות ללא מילים להפרש שטח ריבועים.

הסבירו את האיורים הדינאמיים והראו בדרך אלגברית את נכונות הנוסחה:

(a²-b²)=(a-b)(a+b)

2. מטבעות הזהב

Sample Image

סוחר עשיר אסף מטבעות זהב. יום אחד נשאל "כמה מטבעות זהב יש לך?".

הסוחר הסס לרגע וענה ברמיזה:

"אהההם... אם אחלק את מטבעותיי לשני חלקים אז ההפרש ביניהם יהיה קטן פי 77 מהפרש הריבועים שלהם".

התוכלו לדעת כמה מטבעות זהב לסוחר?

3. מיהו המספר

Sample Image

העלו מספר דו ספרתי בריבוע, הפכו את סדר ספרותיו והעלו גם בריבוע.

הפרש הריבועים יצא גם הוא ריבוע.

התדעו מהו המספר?

4. קסמי חשבון

א. בחרו שני מספרים עוקבים, חשבו את הפרש הריבועים שלהם.

האם קיבלתם את סכום שני המספרים שבחרתם? הכיצד?

ב. בחרו שני מספרים הנבדלים זה מזה ב-2.

חשבו את הפרש הריבועים שלהם ואת סכומם. התדעו מה הקשר? הסבירו.

ג. בחרו שני מספרים הנבדלים זה מזה ב-3.

חשבו את הפרש הריבועים שלהם ואת סכומם. התדעו מה הקשר? הסבירו.

ד. התוכלו לדעת במה נבדלים שני מספרים זה מזה כאשר הפרש ריבועים שלהם גדול פי 77 מסכומם?

(ע"פ המאמר - Revisiting a Difference of Squares, David Slavit, Mathematics Teacher, February 2001)

5. משחקים במחשבון

Sample Image

זיו שיחק במחשבון וקיבל כמה תוצאות מפתיעות:

65²-35²=3000

55²-45²=1000

85²-65²=3000

א. התוכלו למצוא עוד זוגות מספרים שהפרש הריבועים שלהם יתן כפולה של 1000?

ב. התוכלו למצוא שני מספרים שהפרש הריבועים שלהם 5000?

ג. רון הצטרף לשעשועי החישובים ומצא גם הוא תופעה מפתיעה:

56²-45²=1111

89²-12²=7777

78²-23²=5555

ד. האם ניתן לקבל גם את המספרים הבאים 3333, 9999, 8888? הסבירו כיצד.

6. משפטון פרמה

Sample Image

פרמה, מתמטיקאי צרפתי נודע מהמאה ה-17, עסק בתורת המספרים .

פרמה גילה כי כל מספר ראשוני הגדול מ-2 , ניתן להציג באופן אחד ויחיד כהפרש של שני ריבועים.התוכלו להוכיח?

רמז באיור המצורף ללא מילים:

Sample Image

מקור: אתרו של דוד שי, המשפט האחרון של פרמה

למתעניינים, מקורות נוספים:

בעיה ופתרונה - גליונות לחשבון, שמואל אביטל