- עמוד הבית
- הכרות עם פונקציות
הכרות עם פונקציות
הרחבת עולם הפונקציות לתלמיד| הרחבת עולם הפונקציות למורה| لطالب باللغة العربية
יחידת לימוד לכיתה המדעית.
ביחידה זו נעסוק בהרחבה ובהעמקה של מושג הפונקציה. בפרט נחקור הזזות ומתיחות של פונקציות שונות. נתחיל בהכרות של הזזות ומתיחות בהקשר של בעיות אורייניות, בעיות מילוליות המתארות מצבים מחיי היום יום. נבחן את המשמעות של הזזות ומתיחות של פונקציות בגרפים ובביטויים האלגבריים. בהמשך נתבונן בהזזות ומתיחות של גרפים שונים, שלא בהכרח אנו מכירים את התבנית האלגברית שלהן. נבחין בין פעולות אנכיות לאופקיות. בחלק האחרון של היחידה, נכיר את פונקצית השורש כפונקציה ההפוכה לפונקציה הריבועית, ושוב נעמיק ונחקור כיצד באות לידי ביטוי פעולות ההזזות והמתיחות על פונקצית השורש. במהלך היחידה מומלץ (אך לא הכרחי) להשתמש ביישומונים הדינאמיים המשולבים ביחידה, המאפשרים לראות את פעולת ההזזות והמתיחות באופן חזותי ומוחשי וכתנועה חיה של הגרפים.
תיאור: הפעילות עוסקת הכרות עם פונקציית הערך המוחלט ועם ההזזות שלה במקביל לציר ה- y. הגרף של פונקציית הערך המוחלט מורכב משתי קרניים – שני חלקים של קווים ישרים. על כן מתאים לגשר באמצעותו בין הפונקציה הקווית לפונקציה הריבועית. כאן אפשר להתחיל לדון במושגים: תחום עליה ותחום ירידה, ונקודת מינימום. הזזות, מתיחות ושיקוף ביחס לציר ה-x יובילו לגרפים שיהוו בסיס טוב להזזות, מתיחות ושיקוף ביחס לציר ה-x עבור הפונקציות הריבועיות. לפעילות זו יש פעילות המשך, העוסקת בהזזות במקביל לציר ה-x ומשלבת את שתי ההזזות.
תיאור: הפעילות עוסקת בהזזה האופקית של גרף הפונקציה ומתאימה לשילוב בהוראה לאחר ההיכרות עם משפחת הפונקציות ועם ההזזה האנכית. השאלה האחרונה בפעילות עוסקת בשילוב שתי ההזזות יחד: האנכית והאופקית. הפעילות מגשרת בין הפונקציה הקווית לפונקציה הריבועית ומציגה את מושג ההזזה על פונקציה פשוטה. באופן זה מורחב אוסף הפונקציות עליהן מבצעים את פעולות ההזזה ומוטמע מושג ההזזה במנותק מהפונקציה הריבועית.
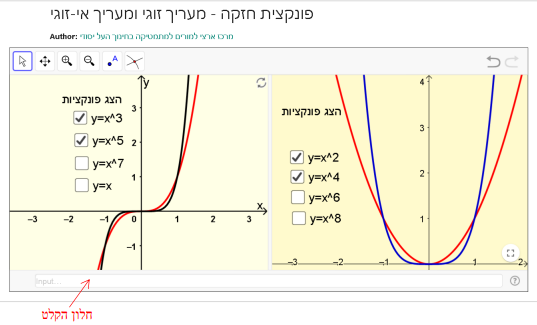
תיאור: הפעילות עוסקת בפונקציות החזקה עם מעריך טבעי, והיא אחת מתוך אוסף פעילויות שמפגישות את התלמידים עם משפחות שונות של פונקציות, במטרה להכיר תכונות משותפות שיש לפונקציות במשפחות השונות, ולהעשיר את השפה המתמטית המאפשרת גם לתאר את תכונות הפונקציות, וגם להצדיקן לא על סמך מראה עיניים בלבד. ההיכרות עם פונקציות החזקה חשובה במיוחד, היות והן מהוות בסיס ללימודי האנליזה בכיתה יוד. לפעילות מצורף יישומון, שמציג את שתי הקבוצות של הפונקציות במשפחה זו לצד זו.
תיאור: פעילות זו עוסקת במשפחת הפונקציות (y=1/(x^n כאשר n מספר טבעי.
הגרפים של הפונקציות הללו מזמנים שיח מתמטי מעמיק בתכונות מיוחדות ומפתיעות עבור התלמידים: הם לא ניתנים לסרטוט במשיכת קולמוס אחת ו"נצמדים" לצירים.
מודגש כי הדיון במושגים: אי-רציפות ואסימפטוטות נעשה בשפה פשוטה שלא מערערת את הביטחון של התלמידים ביכולתם להבין הסברים מתמטיים ואין כוונה לעסוק במושגים אלה באופן מפורש ובאמצעות סימונים מתמטיים והגדרות מדוייקות.
הפעילות מלווה ביישומונים, אליהם ניתן להגיע גם באמצעות סריקת ברקוד, ומצורפים אליה גרפים שניתן לצלם עבור התלמידים, כדי לאפשר עבודה ללא מחשב.
תיאור: אוסף משימות קצרות שמטרתן לחדד, להעמיק את ההבנה ולעורר שיח מתמטי בכיתה. המשימות מתאימות לתלמידי כיתה ט' ברמות הגבוהות. השאלות עוסקות בתכונות של פונקציות לפני חקירה – קדם אנליזה – כמו נקודות חיתוך עם הצירים, תחומי עלייה וירידה ונקודות קיצון, טרנספורמציות אלמנטריות של פונקציות. השאלות מתייחסות לגרפים של פונקציות ללא ביטויים אלגבריים.
נושא: הכרות עם פונקציות
כיתה: ט – י
תיאור: בעזרת יישומון זה ניתן לשקף גרף של פונקציה f(x) (פונקציית הקלט) ביחס לציר ה- Y ולראות את הגרף המתקבל g(x) )פונקציית הפלט(.
נושא: הכרות עם פונקציות
כיתה: ט – יא
תיאור: בעזרת יישומון זה ניתן לשקף גרף של פונקציה f(x) (פונקציית הקלט) ביחס לציר ה- x ולראות את הגרף המתקבל g(x) )פונקציית הפלט(.
נושא: הכרות עם פונקציות
כיתה: ט – י
תיאור: יישומון זה מציג גרפים של פונקציות מהמשפחה: y=x^n עם מעריך טבעי. הגרפים מוצגים בשני חלונות נפרדים, חלון לפונקציות עם מעריך זוגי וחלון לפונקציות עם מעריך אי-זוגי. היישומון מאפשר לנהל שיח כיתתי שיעסוק בתכונות משפחת פונקציות החזקה עם מעריך טבעי, על שני חלקיה. ניתן גם לחבר עבור התלמידים משימות שבהן משולב היישומון. דוגמאות למשימות המבוססות על יישומון זה אפשר למצוא בפעילות "פונקציית חזקה ממעלה זוגית וממעלה אי-זוגית".
נושא: הכרות עם פונקציות
כיתה: ט – י
תיאור: בעזרת היישומון ניתן לנהל שיח כיתתי שיעסוק בחקר הקשר בין תכונות הגרפים של פונקציות לבין הגרפים של הפונקציות המתקבלות מהכפלת ערכי הפונקציה בקבוע חיובי. לחילופין ניתן לחבר פעילויות לתלמידים שמנחות חקר כנ"ל ולשלב בהן את היישומון (ראו דוגמה בפעילות "מתיחה אנכית וכיווץ אנכי של גרף של פונקציה").
נושא: הכרות עם פונקציות
כיתה: ט - י
תיאור: היישומון מאפשר לנהל שיח כיתתי שיעסוק בתכונות משפחת פונקציות זו, על שני חלקיה. ניתן גם לחבר עבור התלמידים משימות שבהן משולב היישומון. דוגמאות למשימות המבוססות על יישומון זה אפשר למצוא בפעילות "משפחת הפונקציות y=1/x^n מעריך טבעי".
נושא: הכרות עם פונקציות
כיתה: ט - י
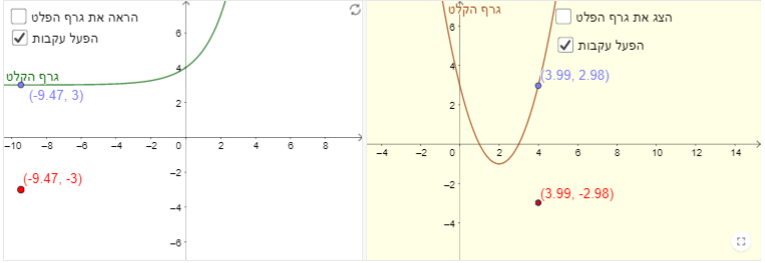
תיאור: היישומון מופיע בפעילות: פונקציות מבעד למראה – שיקופים ביחס לצירים. היישומון מאפשר התבוננות בגרף של פונקציה המתקבל מגרף אחר באמצעות שיקוף בציר Y. ההתבוננות יכולה להיות נקודתית (עקבות) או כללית. היישומון מצורף לפעילות שמפגישה את התלמידים, באמצעות שתי "מכונות", עם שתי טרנספורמציות פשוטות: האחת מבצעת שיקוף ביחס לציר ה-X. האחרת מבצעת שיקוף ביחס לציר ה- Y.
נושא: הכרות עם פונקציות
כיתה: י' או י"א
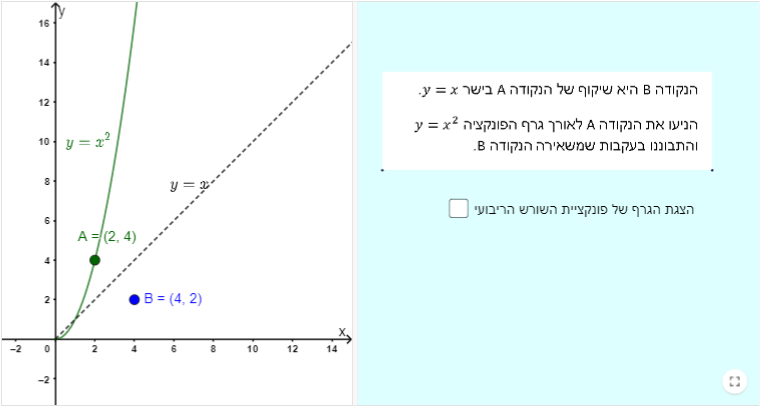
תיאור: היישומון מופיע בפעילות: אל הגרף של פונקציית השורש הריבועי, בה פונקציית השורש הריבועי והגרף שלה מוצגים באמצעות הקשר ביניהם לבין הענף החיובי של הפונקציה .y=x^2 ההיכרות עם הקשרים בין שתי הפונקציות האלה זורעת זרעים לקראת פעילות המשך, העוסקת בין הנגזרות של שתי הפונקציות האלה. ביישומון הדינמי גוררים נקודה על גרף הפונקציה y = x^2 ורואים את שיעורי הנקודה המתקבלת ממנה באמצעות שיקוף בישר y=x.
נושא: הכרות עם פונקציות
כיתה: י - י"א
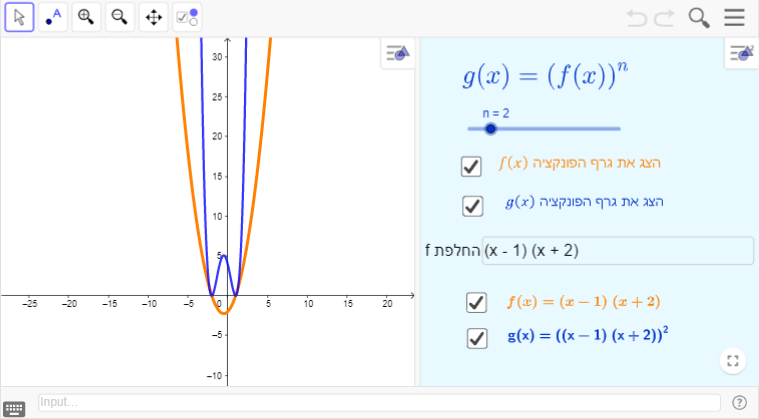
תיאור: יישומון זה מאפשר לנהל שיח כיתתי על תכונות של פונקציות שהן הרכבה של פונקציות חזקה עם מעריך טבעי (x^n) על פונקציה אחרת, כלומר פונקציות מהצורה: (f(x)^n), n מספר טבעי, ועל הקשר בין פונקציות אלה לבין הפונקציות הפנימיות שלהן. היישומון מאפשר, באמצעות סרגל גרירה לשנות את המעריך ולדון בתכונות שמאפיינות גרפים המתקבלים ממעריכים זוגיים לעומת תכונות של גרפים שמתקבלים ממעריכים אי-זוגיים.
נושא: הכרות עם פונקציות
כיתה: ט - י
תיאור: היישומון מופיע בפעילות: פונקציות מבעד למראה – שיקופים ביחס לצירים. היישומון מאפשר התבוננות בגרף של פונקציה המתקבל מגרף אחר באמצעות שיקוף בציר X. ההתבוננות יכולה להיות נקודתית (עקבות) או כללית. היישומון מצורף לפעילות שמפגישה את התלמידים, באמצעות שתי "מכונות", עם שתי טרנספורמציות פשוטות: האחת מבצעת שיקוף ביחס לציר ה-X. האחרת מבצעת שיקוף ביחס לציר ה- Y.
תיאור: יישומון זה מציג גרפים של פונקציות מהמשפחה: y=x^n עם מעריך שלם שלילי. הגרפים מוצגים בשני חלונות נפרדים, חלון לפונקציות עם מעריך זוגי וחלון לפונקציות עם מעריך אי-זוגי. היישומון מאפשר לנהל שיח כיתתי שיעסוק בתכונות משפחת פונקציות זו, על שני חלקיה. ניתן גם לחבר עבור התלמידים משימות שבהן משולב היישומון. דוגמאות למשימות המבוססות על יישומון זה אפשר למצוא בפעילות "משפחת הפונקציות: y=1/x^n מעריך טבעי".
תיאור: בעזרת יישומון זה ניתן להציג במערכת צירים אחת גרף של פונקציה f(x) וגרף של פונקציה g(x) המתקבלת ממנה על ידי הכפלתה בקבוע חיובי, כלומר g(x)=af(x). את ערכו של a אפשר לשנות באמצעות פס הגרירה. אפשר להחליף פונקציות ולראות את הייצוגים האלגבריים והגרפיים של הפונקציה המקורית ושל זו המתקבלת מהכפלתה בקבוע חיובי (a>0) בהתאם לערך של a תהיה זו מתיחה אנכית (a>1) או כיווץ אנכי (0<a<1). יש אפשרות להסתיר את הפונקציה המתקבלת מהמתיחה או מהכיווץ ולבקש מהתלמידים לשער כיצד ייראה הגרף שלה ואח"כ לבדוק בעזרת היישומון. אפשר לשנות את הפונקציה הנתונה לכל פונקציה אחרת (פולינומית, רציונאלית, שורש, טריגונומטרית ועוד). בעזרת היישומון ניתן לנהל שיח כיתתי שיעסוק בחקר הקשר בין תכונות הגרפים של פונקציות לבין הגרפים של הפונקציות המתקבלות מהכפלת ערכי הפונקציה בקבוע חיובי. לחילופין ניתן לחבר פעילויות לתלמידים שמנחות חקר כנ"ל ולשלב בהן את היישומון (ראו דוגמה בפעילות "מתיחה אנכית וכיווץ אנכי של גרף של פונקציה").
תיאור: יישומון זה מציג גרפים של פונקציות מהמשפחה: y=x^n עם מעריך טבעי. הגרפים מוצגים בשני חלונות נפרדים, חלון לפונקציות עם מעריך זוגי וחלון לפונקציות עם מעריך אי-זוגי. היישומון מאפשר לנהל שיח כיתתי שיעסוק בתכונות משפחת פונקציות החזקה עם מעריך טבעי, על שני חלקיה. ניתן גם לחבר עבור התלמידים משימות שבהן משולב היישומון. דוגמאות למשימות המבוססות על יישומון זה אפשר למצוא בפעילות "פונקציית חזקה ממעלה זוגית וממעלה אי-זוגית".
תיאור: בעזרת יישומון זה ניתן לשקף גרף של פונקציה f(x) (פונקציית הקלט) ביחס לציר ה-x ולראות את הגרף המתקבל g(x) (פונקציית הפלט). אפשר להציג את גרף הפונקציה המתקבל משיקוף ביחס לציר ה-x או להסתירו ולבקש מהתלמידים לשער כיצד ייראה הגרף ואח"כ לבדוק בעזרת היישומון. אפשרות נוספת היא להשתמש ב"סרטוט באמצעות עקבות" ולעקוב אחר השיקוף של כל אחת מהנקודות שעל גרף הפונקציה הנתונה עד לקבלת הגרף שהוא שיקוף בציר ה-x .אפשר גם לשנות את הפונקציה הנתונה לכל פונקציה אחרת (פולינומית, רציונאלית, שורש, טריגונומטרית ועוד). בעזרת היישומון ניתן לנהל שיח כיתתי שיעסוק בחקר הקשר בין תכונות הגרפים של פונקציות לבין הגרפים של הפונקציות המתקבלים משיקוף ביחס לציר ה-x .לחילופין ניתן לחבר פעילויות לתלמידים שמנחות חקר כנ"ל ולשלב בהן את היישומון.
תיאור: בעזרת יישומון זה ניתן לשקף גרף של פונקציה f(x) (פונקציית הקלט) ביחס לציר ה-y ולראות את הגרף המתקבל h(x) (פונקציית הפלט). אפשר להציג את גרף הפונקציה המתקבל משיקוף ביחס לציר ה-y או להסתירו ולבקש מהתלמידים לשער כיצד ייראה הגרף ואח"כ לבדוק בעזרת היישומון. אפשרות נוספת היא להשתמש ב"סרטוט באמצעות עקבות" ולעקוב אחר השיקוף של כל אחת מהנקודות שעל גרף הפונקציה הנתונה עד לקבלת הגרף שהוא שיקוף בציר ה-y .אפשר גם לשנות את הפונקציה הנתונה לכל פונקציה אחרת (פולינומית, רציונאלית, שורש, טריגונומטרית ועוד). בעזרת היישומון ניתן לנהל שיח כיתתי שיעסוק בחקר הקשר בין תכונות הגרפים של פונקציות לבין הגרפים של הפונקציות המתקבלים משיקוף ביחס לציר ה-y .לחילופין ניתן לחבר פעילויות לתלמידים שמנחות חקר כנ"ל ולשלב בהן את היישומון.
תיאור: פעילות זו עוסקת במתיחה אנכית ובכיווץ אנכי של גרף של פונקציה. בהמשך לפעילות זו תוצע גם פעילויות העוסקת במתיחה אופקית ובכיווץ אופקי של גרף של פונקציה.
מטרות הפעילות הן:
- להעמיק את ההבנה של הקשר בין גרף פונקציה לבין גרף הפונקציה המתקבל מהכפלת ערכי הפונקציה בקבוע.
- לפתח "חוש לפונקציות".
- לזהות ולנתח פונקציות וגרפים של פונקציות באופן איכותני.
- להכיר ולהרחיב את מאגר הפעולות הנעשות על פונקציות.
- ליצור שיח מתמטי סביב המושג מתיחה אנכית וכיווץ אנכי של גרף של פונקציה כתשתית להבנת מושגים באנליזה.
תיאור: פעילות זו עוסקת בשיקופים של פונקציות ביחס לציר ה-x וביחס לציר ה-y. לתלמידים מוצגות שתי מכונות המבצעות את השיקופים. עליהם לחקור את התכונות שנשארות ואת התכונות שמשתנות תחת כל אחד מהשיקופים. לפעילות מצורף יישומון, בו אפשר להחליף פונקציות ולראות את השיקופים שלהן בעזרת סימון – "הראה גרף הפלט" או בעזרת סימון עקבות. התובנות שנרכשות באמצעות הפעילות מתווספות ל"ארגז הכלים" של התלמידים, כך שיוכלו להשתמש בהן עבור פונקציות אחרות. הפעילות מניחה בסיס גם להבנה של המושגים פונקציה זוגית ופונקציה אי-זוגית.
מומלץ לבצע פעילות זו אחרי פעילות הפתיחה "פונקציות מבעד למראה - שיקופים" המופיעה באתר המרכז הארצי למורים למתמטיקה בחינוך העל-יסודי.
תיאור: פעילות הפתיחה שלפניכם מפגישה את התלמידים, באמצעות שתי "מכונות" עם שתי טרנספורמציות פשוטות: האחת מבצעת, לכל נקודה על הגרף, שיקוף ביחס לציר ה-x, האחרת מבצעת שיקוף ביחס לציר ה-y. מבחינה אלגברית: האחת מתאימה לכל מספר את המספר הנגדי לזה המותאם בפונקציה המקורית, האחרת מתאימה לכל מספר את המספר שמותאם בפונקציה המקורית למספר הנגדי שלו.
מטרת הפעילות היא פיתוח יכולת זיהוי של גרף שהתקבל מהפעלה של שיקוף ביחס לאחד הצירים והתאמת הקשר האלגברי המתאים. העיסוק והדיון בתכונות הנשמרות והמשתנות בעקבות ההפעלה של כל אחת מהטרנספורמציות הנ"ל מעמיקים את ההבנה של מושג הפונקציה. לשיקול המורה קישור למושגים פונקציה זוגית ופונקציה אי-זוגית.
לפעילות מצורפים יישומונים.
