- עמוד הבית
- מרובעים
מרובעים
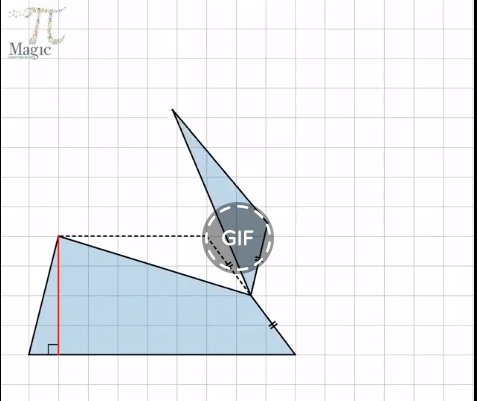
מקור: אתר הפייסבוק של עידן טל
אופי הפעילות: תמונה דינאמית ממחישה ומעוררת דיון כיתתי
תיאור: התמונה ממחישה בתהליך דינאמי את השיוויון של סכום המרחקים של נקודה כלשהי בתוך משולש שווה צלעות מצלעותיו לאורך הגובה של המשולש.
התמונה לא מספקת הוכחה למשפט.
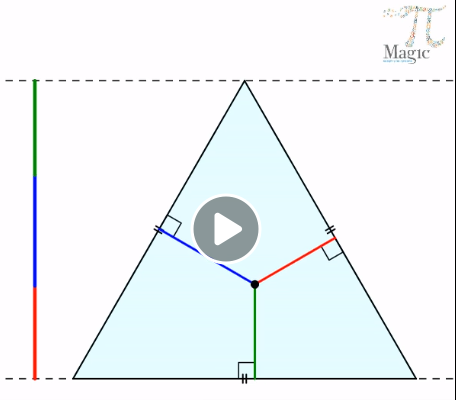
מקור: אתר הפייסבוק של עידן טל
אופי הפעילות: תמונה דינאמית ממחישה ומעוררת דיון כיתתי
תיאור: התמונה ממחישה את הנוסחה לשטח דלתון ע"י "הפיכתו" למלבן ששטחו בדיוק כפליים משטח הדלתון.
ההוכחה נובעת בקלות מהתבוננות בתמונה הדינאמית.
מקור: מטח
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: ביישומון אפשר לבנות מרובעים לפי תכונות אלכסונים שבוחרים מתוך שלושה תפריטים העונים על שלוש שאלות: האם האלכסונים חוצים זה את זה? האם האלכסונים מאונכים זה לזה? האם האלכסונים שווים זה לזה? בחלון המידות יופיעו: בשחור - הנתונים של אלכסוני המרובע שבניתם, בכחול - אורכי הצלעות ומידות הזוויות של המרובע. אפשר לבנות מרובע אחר לפי אותן תכונות של האלכסונים ע"י גרירה של קדקודי המרובע או ע"י לחיצה על בנו מרובע אחר מאותו הסוג.
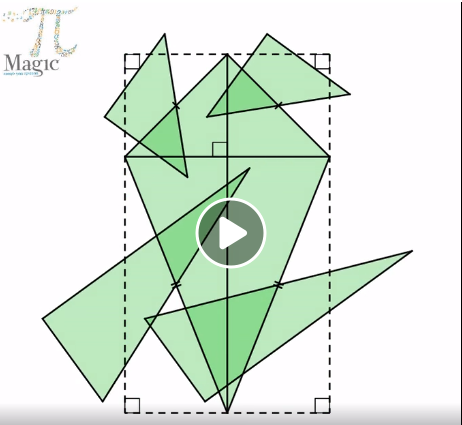
מקור: אתר הפייסבוק של עידן טל
אופי הפעילות: תמונה דינאמית ממחישה ומעוררת דיון כיתתי
תיאור: התמונה הדינאמית מציגה דלתונים קעורים וקמורים, מציגה את המעוין כמקרה פרטי של דלתון וממחישה תכונות משותפות לכל הדלתונים.
* אין לשכוח שתמונה דינאמית אינה מספקת הוכחה. יש להשלים הוכחה מדויקת בסיום הדיון שמתקיים בכיתה בעקבות הצפייה בתמונה הדינאמית.
מקור: מטח
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: ביישומון (Applet) משפחת המרובעים אפשר לבנות מרובעים מסוגים שונים על ידי בחירת המרובע הרצוי מתוך תפריט. בחלון המידות יופיעו: סוג המרובע שבחרתם, אורכי הצלעות ומידות הזוויות. אפשר להציג את אלכסוני המרובע, ובחלון המידות יופיעו אורכי האלכסונים והמרחקים מהקדקודים עד נקודת החיתוך של האלכסונים. אפשר לבנות מרובע אחר מאותו הסוג על ידי גרירה של קדקודי המרובע או על ידי לחיצה על בנו מרובע אחר מאותו הסוג.
מקור: מרכז מורים ארצי למתמטיקה בחינוך העל יסודי
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: דף עבודה ויישום דינאמי לחקירת תכונות האלכסונים בטרפז. בדף העבודה הנחיות לחקירה והוכחה של המשפט: הקו המקביל לאלכסוני הטרפז ועובר דרך נקודת מפגש האלכסונים שווה לממוצע ההרמוני של הבסיסים.
מקור: מרכז מורים ארצי למתמטיקה בחינוך העל יסודי
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: דף עבודה ויישום דינאמי בהם מוצגים שישה ריבועים, אך עם גרירת הקודקודים הם משתנים. המשימה לזהות כיצד נבנה כל מרובע ולאפיין אותו. מה מיוחד בריבוע?
מקור: המרכז הארצי למתמטיקה בחינוך העל יסודי
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: יישום דינאמי בו יש להוכיח כי קיים מלבן ששטחו שווה לשטח המקבילית . או במילים אחרות המחשה לכך ששטח כל המקביליות עם צלע נתונה (a) וגובה נתון (h) שווה, והוא שווה לשטח המלבן שאורך צלעותיו כצלע המקבילית והגובה.
מקור: המרכז הארצי למתמטיקה בחינוך העל יסודי
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: דף עבודה אינטראקטיבי ויישום דינאמי בגאוגברה לחקר בעיה בגיאומטריה. הבעיה עוסקת בתכונות המלבן ושטח משולש.
מקור: מתמטיקה משולבת, מכון וייצמן
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: דף עבודה אינטראקטיבי בגאוגברה לחקירה של בעיה בגיאומטריה. בהינתן מרובע כלשהו נעביר דרך קודקודיו מקבילים לאלכסוניו. איזה מרובע נקבל? בדף העבודה הנחיות לחקירה של מצבים שונים ובחינת התכונות של משפחת המרובעים.
מקור: המרכז הארצי למתמטיקה בחינוך העל יסודי
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: דף עבודה אינטראקטיבי ויישום דינאמי בגאוגברה לחקר בעיה בגיאומטריה. בהינתן מרובע כלשהו, ניצור מרובע פנימי ששניים מקודקודיו על אמצעי האלכסונים והשניים האחרים על אמצעי צלעות מנוגדות של המרובע. בדף העבודה הנחיות לבנייה בגאוגברה. מבוסס על בחינת בגרות: שאלון 804, קיץ תשע"ב, שאלה 4 .
מקור: מתמטיקה משולבת, מכון וייצמן
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: דף עבודה אינטראקטיבי בגאוגברה לחקירה של בעיה בגיאומטריה. בהינתן מרובע כלשהו איזה מרובע נקבל אם נחבר את אמצעי צלעותיו? איזה מרובע פנימי נקבל ממלבן. ולהיפך, מאיזה מרובע חיצוני נקבל מרובע פנימי מלבן? מה הקשר בין השטחים? מה עוד ניתן לשאול? מקור: מתמטיקה משולבת, מכון וייצמן.
מקור: המרכז הארצי למתמטיקה בחינוך העל יסודי
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: פיצוח העוסק בתכונות מרובעים שאלכסוניהם מאונכים. בשאלה הראשונה חוקרים את המרובעים השונים ואת שטחיהם, תוך קיפולי נייר ושימוש ביישום דינאמי. בבעייה השנייה מחפשים מעוין החסום במלבן. בעיה זו דורשת הכרות עם תכונות המרובעים ובפרט המעוין וכן שימוש במשפט פיתגורס ובאלגברה.
מקור: Maths is Fun
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: כלי אינטראקטיבי המציג את סוגי המרובעים השונים ואת תכונותיהם. ניתן לשנות את מימדי כל מרובע ולחקור מה משתנה ומה נשאר קבוע.
מקור: illuminations
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: הדגמה אינטראקטיבית כיצד ניתן לחלק את המקבילית לשני שטחים וליצור ממנה מלבן ועל ידי כך לפתח את הנוסחה לשטח מקבילית ובכל לגלות את נוסחת השטח של מקבילית.
מקור: illuminations
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: אלכסוני המרובע יכולים להיחתך באופנים שונים: הם יכולים להיות מאונכים זה לזה, הם יכולים להיות שווים או לא, אחד מהם עשוי לחצות את השני, או ששניהם חוצים זה את זה. בפעילות זו חוקרים אילו סוגים של מרובעים ניתן ליצור על פי תכונות נתונות של האלכסונים. מלווה בתכנון שיעור ובדפי עבודה (אנגלית).
מקור: illuminations
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: יישום דינאמי לחקירת השטחים של משולש ושל טרפז ומקבילית. בכלי ניתן לאסוף ממצאים של אורכי הצלעות והגבהים ולמצוא את הקשר שלהם לנוסחת השטח. נשאלת השאלה נה הדומה ומה השונה בין נוסחאות השטח השונות.
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי.
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: בפיצוח בעיות למציאת שטחים של מרובעים ומשולשים.
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: הפיצוח כולל אוסף בעיות לחישוב שטחים החסומים באופנים שונים בתוך ריבוע. הבעיות מזמנות חקירה וחשיבה יצירתית.
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: משחק אינטראקטיבי לזיהוי של ריבועים בתוך רשת קורדינטות . מלווה בפיצוח.
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: הפיצוח כולל שתי בעיות גיאומטריות במישור אשר ניתן להכלילן לגיאומטרית המרחב. הבעיה הראשונה מתאימה גם לתלמידי חט"ב ודורשת ידע בחישוב שטחים ונפחי פירמידה. הבעיה השניה דורשת שימוש במשפט פיתגורס ופתרון מערכת משוואות. הבעיות מזמנות חקירה ופיתוח ראיה מרחבית.
