הנקודה שבפנים

תקציר| הנקודה שבפנים| نقطة في الداخل

1. חלוקת שטחים 

במגרש כדורגל הציב השופט את הכדור בנקודה P בתוך הריבוע וחילק את שטח המגרש לשתי הקבוצות באופן הבא:

קבוצה א תקבל את השטח הכתום S1+S3.

קבוצה ב תקבל את השטח הסגול S2+S3.

תוכלו להיעזר ביישום הדינאמי  לשם החישובים עבור נקודות P שונות.

א. היכן לדעתכם יש למקם את הנקודה P כך שהחלוקה תהיה הוגנת? מדוע?

ב. כיצד תשתנה החלוקה (אם בכלל) אם המגרש יהיה מלבני? נמקו.

שוב תוכלו להיעזר ביישום הדינאמי  לשם שינוי מימדי המלבן.

ג. כיצד תשתנה  החלוקה (אם בכלל) אם הנקודה תהיה מחוץ למגרש? נמקו.

 2. חלוקת נפחים

נתונה תיבה מלבנית ובתוכה נלכד עכביש בנקודה P שהיא מרכז התיבה. העכביש מתח חוטים לפינות התיבה כך שיצר פירמידות אשר קודקוד הראש שלהן הנקודה P ובסיסן פאות

התיבה.

א. כמה פירמידות נוצרו באופן זה?

ב. מה תוכלו לומר על סכום הנפחים של שתי פירמידות נגדיות (שבסיסן מונח על פיאות נגדיות).

ג. כיצד ישתנו הנפחים אם הנקודה P תנוע למקום אחר במרחב התיבה? נמקו.הנחיה – ניתן להיעזר בפתרון השאלה הקודמת.

3. המרחק הנעלם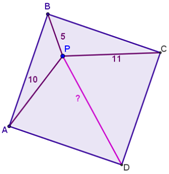  

במגרש כדורגל ריבועי נמצא השחקן בנקודה P.

ידוע לו כי מרחקו מפינת המגרש בקודקוד A הוא 10מטרים, מהקודקוד B הוא 5 מטרים ומהקודקוד C הוא 11 מטרים. בשאלות הבאות תוכלו להיעזר ביישום הדינאמי  .

א. התוכלו לעזור לו ולקבוע מהו מרחקו מפינת המגרש בקודקוד D?

ב. כיצד ישתנה המרחק PD כאשר המגרש יהיה מלבני?

ג.  מה יהיה המרחק PD אם השחקן יהיה מחוץ למגרש?

ד.  מה יהיה המרחק PD אם נתון כי: PB=a ,PA=c ,PC=b?

4. תיבה

נתונה תיבה ובתוכה נלכד עכביש בנקודה P. העכביש מתח חוטים לפינות התיבה כך ש: