ביליארד מתמטי

ביליארד מתמטי

תקציר | ביליארד מתמטי | פתרונות | בערבית

תמר והדר המציאו משחק חדש בהשראת שולחן הביליארד.
כללי המשחק: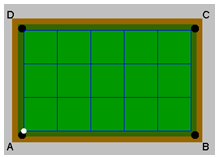 

• המשחק נערך על שולחן מלבני מנייר משובץ.
  ארבע הפינות מסומנות ב- A, B, C, D.
• הכדור הדמיוני יוצא מקודקוד A, ונזרק בזווית של 45^o.
  אם הכדור פוגע בדפנות השולחן הוא ממשיך במסלולו שוב בזווית של 45^o לדופן השולחן.
• הכדור נעצר כאשר הוא מגיע לאחת מפינות השולחן.
• ניתן לשנות את מימדי השולחן.
  
  

1. צפו במשחקון בשולחן 3X5. 
א. באיזו פינה עצר הכדור?
ב. בכמה פגיעות בשולחן הגיע למטרתו?
    (כולל הפגיעות של ההתחלה ושל הסיום).

תוכלו להתנסות במשחק האינטראקטיבי (נדרש תוסף ג'אווה בדפדפן שאינו כרום),  או בעזרת עפרון ונייר, בשולחנות הבאים:

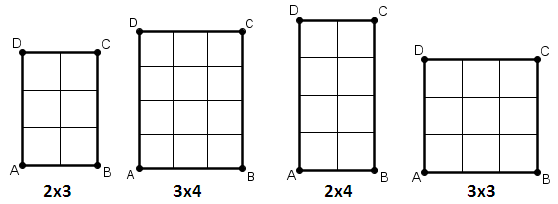
*שימו לה המשחק האינטראקטיבי נתמך java ולכן אינו עובד בדפדפן Chrom.

תמר והדר שיחקו בכל השולחנות הללו ושאלו שאלות מעניינות.

2. האם ישנם שולחנות דומים?
א. תמר שמה לב כי הכדורים בשולחנות 1x2 , 2x4 מתנהגים באופן דומה. הסבירו.
    התוכלו למצוא שולחן נוסף מסוג זה? תוכלו להיעזר במשחק האינטראקטיבי.
ב. הדר טענה שיש בקבוצה זוג אחר של שולחנות דומים. התוכלו לומר מיהם?
    האם יש קשר בין מימדי השולחנות שמצאתם? אם כן מהו?
ג. תנו דוגמה לשולחנות נוספים בעלי התנהגות דומה. בדקו במשחק האינטראקטיבי.

3. האם ניתן לדעת מראש את מספר הפגיעות (כולל ההתחלה והסיום) עד שיגיע הכדור לעצירה?
א. מהו השולחן בעל מספר הפגיעות הקטן ביותר?
    התוכלו לדעת מהו השולחן בעל מספר הפגיעות הגדול ביותר?
ב. הדר מצאה שני שולחנות שונים שבהם מספר הפגיעות (כולל ההתחלה והסיום) הוא 5. מיהם?
ג. תמר סברה כי גם בשולחן 1x4 מספר הפגיעות הוא 5. האמנם?
    האם יש קשר בין מימדי השולחנות שמצאתם ומספר הפגיעות? אם כן מהו?
ד. הדר ביקשה לבדוק האם החוקיות שמצאה אכן עובדת גם במקרים נוספים.
    היא חיפשה שולחנות בהם מספר הפגיעות הוא 7.
    מצאו, בעזרת המשחק האינטרקטיבי, שולחנות נוספים שבהם מספר הפגיעות הוא 7. (hits=7)
    בדקו האם הקשר שמצאתם בין מימדי השולחנות ומספר הפגיעות אכן עובד.

ה. תמר מצאה כי גם בשולחן במימדים של 6x8 מספר הפגיעות הוא 7. הכיצד?
    האם יש צורך לנסח מחדש את החוקיות?
ו. אם ברשותכם שולחן דמיוני של 150x300, התוכלו לדעת מראש מה יהיה מספר הפגיעות?

שחקני הביליארד המקצוענים יודעים כי מהלך מוצלח דורש תכנון מפורט של מסלול הכדורים מבחינה גיאומטרית ופיסיקלית, כמו גם ביצוע מדויק להפליא. 
בולצמן, מענקי הפיסיקה של המאה ה- 19, טען שהתנהגות מולקולות גז בקופסה דומה להתנהגות כדורי הביליארד ולפיה בנה את הבסיס לתורת המכניקה הסטטיסטית, שמהווה אחת מאבני היסוד של הפיזיקה המודרנית. בעקבותיו, במאה ה- 20, התפתחה תיאוריה מתמטית החוקרת את מסלולי הכדורים בביליארד כמערכת דינמית הנשלטת על ידי חוקי התנועה של ניוטון, ואיך האקראיות לכאורה קשורה לתורת הכאוס. קראו עוד על החוקרת בתחום במכון וייצמן, פרופ' ורד רום-קידר.

המתמטיקאים חוקרים מסלולי הכדור גם בשולחנות שאינם מלבניים כמו משולש, אליפסה או תיבה.
קראו עוד ב- Math World

4. האם ניתן לדעת מראש באיזו פינה הכדור יעצור?
הדר ותמר הביאו את המשחק לכיתה.
בכדי לשכלל את המשחק, הן הוסיפו ניקוד לכל משחקון לפי הניקוד הבא:

• כדור שיעצר בפינה A - 100 נקודות
• כדור שיעצר בפינה B - 50 נקודות
• כדור שיעצר בפינה C - 25 נקודות
• כדור שיעצר בפינה D - 10 נקודות

א. באפשרותכם לבחור את גודל השולחן למשחקון. באיזה שולחן תבחרו בכדי לקבל ניקוד הכי גבוה?
ב. אם ברשותכם שולחן דמיוני של 150x300, התוכלו לדעת מראש בכמה ניקוד תזכו?

לשם חקירת החוקיות, תוכלו לרכז את תוצאות המשחקונים בטבלה הבאה:

שאלות חקירה נוספות:

• האם קיים קשר בין אורך המסלול הכדור עד לעצירתו לבין מימדי השולחן?
• אילו סוגי סימטריה ניתן למצוא במסלול הכדור בשולחנות השונים?
  לאילו שולחנות ניתן למצוא סימטריה שיקופית לקו אנכי?
  לאילו שולחנות ניתן למצוא סימטריה שיקופית לקו אופקי?
  לאילו שולחנות ניתן למצוא סימטריה סיבובית?
• העלו גם אתם שאלות נוספות לחקירה של שולחנות הביליארד.

מקור הפעילות - Paper Pool: Analyzing Numeric and Geometric Patterns - NCTM, illuminations