• בעיות תנועה
• פתרון גרפי

 תקציר| בתנועה מתמדת| פתרונות| حركتنا مستم ّرة

1. שני חברים יצאו לדרך, בים בם בום.... 

תמי וניר שכנים בבית משותף ולומדים באותה כיתה. כל בוקר הם יוצאים יחדיו ברגל מביתם בשביל המוביל לבית הספר. יום אחד הם התחילו ללכת ביחד באותו קצב (v₁).

ניר המשיך ללכת באותה המהירות מחצית מהזמן ולאחר מכן הלך במהירות איטית יותר (v₂) עד הגיעו לבית הספר. לעומתו תמי המשיכה באותה מהירות חצי מהדרך (v₁), ובמחצית השנייה של הדרך, האטה והלכה במהירות האיטית של ניר (v₂).

א. התוכלו לקבוע מי הגיע ראשון לבית הספר?

ב. אם היו תמי וניר מתחילים במהירות איטית יותר, ולאחר מכן מגבירים את הקצב.
   מי אז היה מגיע ראשון לבית הספר ?

הנחיה – תארו את הבעיה במערכת צירים והיעזרו ביישום הדינאמי.

2. ארבעה כלי רכב יצאו לדרך 

אופניים, טרקטור, אופנוע ומכונית נסעו בכביש דו סטרי, כל אחד מהם במהירות קבועה משלו.

המכונית עקפה את הטרקטור בשעה 12:30 , חלפה על פני האופניים בשעה 13:00 ופגשה את האופנוע בשעה 13:30. האופנוע פגש את הטרקטור ב- 13:45 וחלף על פני האופניים בשעה 14:15.

באיזו שעה נפגשו האופניים והטרקטור?

הנחיה – תארו את הבעיה במערכת צירים והיעזרו ביישום הדינאמי.
הוכיחו את טענתכם גם באופן אלגברי.

3. חידת הנזיר  

נזיר הינדי יצא מכפרו עם שחר והחל לטפס לאיטו בשביל התלול, המוליך אל המנזר שעל פסגת ההר. הנזיר הספיק להגיע למנזר, לתפילה בשעת השקיעה.

למחרת עם שחר, בדיוק באותה שעה, שהחל לטפס ביום קודם, יצא הנזיר מהמנזר והחל יורד במהירות אל הכפר לאורך אותו שביל. הוא עצר למנוחת צהריים במעיין והמשיך והגיע אל ביתו בכפר בשעת השקיעה.

האם יתכן כי בשני הימים היה מקום שאליו הגיע הנזיר בדיוק באותה שעה גם בעלייה וגם בירידה? 

מקורות: 

• "שאלות מילוליות במשתנה אחד בגישה הגרפית" ,שוש גלעד, הוצאת מטח, 2000 
• nrich

פיצוחים נוספים בנושא בעיות תנועה:

מרוץ מכוניות דינאמי - בפיצוח הפנייה לסימולציה של בעיית תנועה, למאמר העוסק בסגנונות למידה שונים, ובעיות תנועה רבות בספר האלקטרוני "לראות מתמטיקה- פונקציות" של מטח.

בעיות בתנועה בדרך אחרת - הפיצוח עוסק בפתרון בדרכים לא שגרתיות של בעיות תנועה ברמה של 4-5 יח"ל. התנועה מתוארת בגרפים של פונקציות, וסיפור הבעיה ופתרונו נקרא מתוך הגרף.

בעיית תנועה - כוונים מנוגדים - עיבוד של שאלת בגרות ברמת 3 יח"ל, מתוך מאגר היישומים הדינאמיים.

מהר יותר, גבוה יותר וחזק יותר – בעיות תנועה מתוך מציאות האולימפיאדה. שימו לב כי הבעיות מנוסחות קצת אחרת מספרי הלימוד, ובחלקן יש להניח הנחות שאינן נתונות בשאלה, או לחפש נתונים שלא מופיעים בה.

תקציר| ממוצעי פיתגורס ועוד| פתרון| حلول

האגדה מספרת שפיתגורס, המתמטיקאי היווני הנודע מימי יוון הקדומה ( 500 לפנה"ס), עבר פעם ליד חרש ברזל והתאהב בצלילי דפיקות הפטיש שהיו נעימים לאוזנו. הוא בדק ומצא, כי משקלי הפטישים היו 6, 8, 9, ו-12 ק"ג. היחסים בין משקלי הפטישים הפיקו צלילים הרמוניים.

 מה מיוחד כל כך במספרים אלה? שאל.

הוא מצא כי הממוצע החשבוני בין 6 ל-12 הוא   

ואילו הממוצע ההרמוני בין 6 ל-12 הוא   

פיתגורס בדק גם כלי פריטה וגילה שקיים קשר מתמטי בין אורך המיתר, שעליו פורטים, ובין גובה הצליל: כשמתקיים יחס מסוים בין אורכי המיתרים, נוצרת הרמוניה בין הצלילים. כך הפך פיתגורס לראשון שהראה כי יש קשר הדוק בין מדע מדויק לבין מוסיקה.

1. מהירות ממוצעת

א. לטיול השנתי נסענו באוטובוס בכביש המהיר. בשל עומס כבד בתנועה נסע האוטובוס לאיטו במהירות של 40 קמ"ש חצי מהדרך. ובחצי השני של הדרך הצליח להגביר את מהירותו ל-80 קמ"ש. האם מהירותו הממוצעת בדרך כולה הייתה 60 קמ"ש? יותר, או פחות?

ב. באיזו מהירות היה צריך האוטובוס לנסוע בחצי הדרך השנייה בכדי שמהירותו הממוצעת תהיה 80 קמ"ש?

ג. מכונית עברה דרך של 40 ק"מ במהירות ממוצעת של 40 קמ"ש. מה צריכה להיות מהירותה הממוצעת ב-40 הק"מ הבאים כדי שמהירותה הממוצעת לאורך כל 80 הק"מ תהיה 80 קמ"ש?

2. ממוצעים בין מלבן וריבוע

נתון מלבן שמידותיו x ו-y. נשאל את עצמנו שאלות אחדות:

א. מה צריך להיות אורך צלע הריבוע שהיקפו ישווה להיקף המלבן?

ב. מה צריך להיות אורך צלע הריבוע ששטחו ישווה לשטח המלבן?

ג. מה צריך להיות אורך צלע הריבוע שאלכסונו ישווה לאלכסון המלבן?

ד. מה צריך להיות אורך צלע הריבוע שהיחס בין שטחו להיקפו ישווה ליחס בין שטח והיקף המלבן?

הידעתם?

כאשר חוקרים את תפקודם הביולוגי של גופים חיים יש חשיבות עיקרית לא לנפח הגוף בפני עצמו, או לשטח חיצוני של הגוף בפני עצמו, אלא ליחס שבין הנפח לשטח הגוף. באותה מידה בצורות שטוחות יש חשיבות ליחס שבין שטח הצורה להיקפה. למשל, מדינה שקו הגבול שלה ארוך מאוד ביחס לשטחה יש לה בעיות ביטחוניות מסובכות. באיזה ממוצע כדאי להשתמש?

3. מי גדול יותר?

נכיר ארבעה ממוצעים בין שני מספרים a ו- b הנפוצים ביותר. 
שלושת הראשונים נקראים ממוצעי פיתגורס.

א. חשבו את ארבעת הממוצעים השונים בין המספרים 4 ו-12 ובין 9 ו-16. 
סדרו את הממוצעים על פי גודלם. 
בדקו ביישום הדינאמי.

ב. הסבירו על פי האיור הבא מדוע הממוצע החשבוני גדול מן הממוצע הגיאומטרי.

ג. הסבירו על פי היישום הדינאמי מדוע האורכים A, G ו-H הם שלושת ממוצעי פיתגורס של האורכים a ו-b. 
מי גדול ממי?

ד. הוכיחו כי: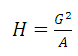 

ה. הוכיחו באיור כי: 

ו. סדרו את ארבעת הממוצעים על פי גודלם.

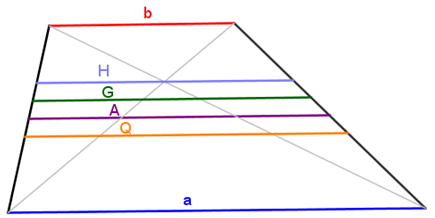4. ארבעה ממוצעים בטרפז

הוכיחו כי:

1. קטע אמצעים בטרפז שווה לממוצע החשבוני של בסיסי הטרפז.

2. קטע מקביל לבסיסי הטרפז המחלק לשני טרפזים דומים שווה לממוצע הגיאומטרי של בסיסי הטרפז.

3. קטע מקביל בטרפז העובר דרך מפגש אלכסוניו שווה לממוצע ההרמוני של בסיסי הטרפז.

4. קטע מקביל לבסיסי הטרפז המחלק לשני טרפזים שווי שטח, שווה לממוצע הריבועי של בסיסי הטרפז.

מקורות והרחבה: 

שלושת הממוצעים – פרופ' אביטל - גליונות לחשבון מס 7

על ממוצעים שונים – פרופ' אביטל – גליונות לחשבון מס 62

ממוצעים ומוסיקה – מייקל נ. פריד – על"ה 30, 2003

שבעה ממוצעים שונים בטרפז – נתן ויזדום - אוניברסיטת ג'ורג'יה

הוכחות ויזואליות ללא מילים (כמעט) - אורית זסלבסקי, גרייסי ויניצקי.  

תקציר| מרובע שכזה| פתרון|  شكل شكل رباعي كهذا

קפלו דף מלבני לאורכו ולרוחבו כך שיתקבלו בפתיחת הדף ארבעה מלבנים חופפים (ראו איור) כעת סמנו על כל קטע מארבעת הקטעים שהתקבלו (הקיפולים) נקודה כלשהי, וחברו את הנקודות כך שיתקבל מרובע.

המרכז הארצי למורים למתמטיקה בחינוך העל יסודי, Created with GeoGebra

1. חשבו ובדקו. תוכלו לנסות מצבים שונים ביישום הדינאמי.

א. אילו מרובעים ניתן לקבל? 

ב. אילו מרובעים לא ניתן לקבל? 

ג. האם ניתן ליצור מרובע קעור?

ד. האם אלכסוני המרובע שהתקבל תמיד יהוו קווי סימטריה?

ה. מה נקבל אם כל הנקודות יהיו באותו מרחק מהנקודה המרכזית (M)?

ו. מה נקבל אם רק זוג אחד של נקודות ימצא במרחק שווה מהנקודה המרכזית? האם יש יותר מאפשרות אחת? 

2. נמצא את שטח המרובע שאלכסוניו מאונכים בעזרת קיפולי נייר.  

גזרו את אחד המרובעים שיצרתם אשר אלכסוניו מאונכים.

א. קפלו שני קודקודים נגדיים אל נקודת המפגש של האלכסונים.

ב. קפלו את שני הקודקודים האחרים אל נקודת מפגש האלכסונים כך שתתקבל מעין מעטפה.

ג. איזה מרובע התקבל? נמקו.
כיצד ניתן לקבל ריבוע?

ד. מה הקשר בין צלעותיו לאלכסוני המרובע המקורי? הסבירו.

ה. איזה חלק מהווה המרובע שהתקבל משטח המרובע המקורי? כיצד מצאתם?

ו. אם ידוע כי אורכי האלכסונים של המרובע הם 6 ו-8 ס"מ. מה שטח המרובעים?
   בדקו ביישום הדינאמי.
   אם נסמן את אורכי האלכסונים של המרובע ב-x ו-y ס"מ. הביעו את שטח המרובעים.

מקורות 

1. המרכז הארצי למורים למתמטיקה בחינוך היסודי, מעובד מתוך הרצאה של ג'וני אוברמן. 
2. "אקפלה" – ספר מאת גיא פז, קיפולי נייר ומתמטיקה.

המשך: איזהו המעוין החסום במלבן

תקציר |מרובע שכזה| פתרון|  شكل شكل رباعي كهذا

במלבן ABCD חסום מרובע APCQ.

1. הזיזו את נקודות Q ו-P ביישום הדינאמי ומצאו את מיקומן כך שהמרובע APCQ יהיה:

א. מקבילית. כמה מקביליות יתכנו?

ב. מעוין. כמה מעוינים יתכנו?

ג. רשמו מהו התנאי לכך שהמרובע יהיה מקבילית? שיהיה מעוין?

המרכז הארצי למורים למתמטיקה בחינוך העל יסודי, Created with GeoGebra

2. ברשותכם מלבן שמידותיו 3x6 סמ"ר.

א. חשבו את אורך צלע המעוין החסום במלבן. (רמז – זוכרים את משפט פיתגורס?)

ב. חשבו מהו היחס בין שטח המעוין לשטח המלבן.

ג. שנו ביישום הדינאמי את גובה המלבן (גררו את הנקודה C). האם עדיין המרובע החסום הוא מעוין? האם השתנה יחס השטחים? הסבירו.

3. ברשותכם נייר מדפסת A4 (אשר יחס צלעות המלבן שלו הן )

א. חשבו את אורך צלע המעוין החסום במלבן.

ב. חשבו את היחס בין שטח המעוין לשטח המלבן.

ג. לפניך נייר בגודל A4.

הסתמכו על תכונות המעוין והראו כיצד ניתן לקפלו כך שיהיה חסום בתוכו מעוין.

4. ברשותכם מלבן שמידותיו axb סמ"ר.

א. הביעו בעזרת a ו-b את אורך צלע המעוין החסום במלבן.

ב. הביעו בעזרת a ו-b את היחס בין שטח המעוין לשטח המלבן.

ג. הראו בדרך אלגברית ובדרך גיאומטרית כי קיים מעוין אחד בלבד החסום במלבן.

הקודם: מרובע שכזה - שאלכסוניו מאונכים

תקציר| פרבולות בתנועה| פתרונות

א. צפו בפרבולה המתנועעת בכל אחד מהסרטונים. 
מצאו מהי התבנית האלגברית, עם פרמטר אחד בלבד, שיוצרת את תנועת הפרבולה. שימו לב באיזה ייצוג של הפונקציה הריבועית כדאי להשתמש.

1. הפרבולה מטפסת על מגדל

2. הפרבולה בים

3. לטפס על קשת בענן (ישר)

1.

4. שתי פרבולות בתנועה זו אל זו

5. הפרבולה מתגלגלת על הקשת (פרבולה)

ב. צפו בריקוד הפרבולות בסרטון הבא:

מצאו מהי התבנית האלגברית של כל אחת מארבע הפרבולות, עם פרמטר אחד בלבד, שיוצרות את תנועתן. 
שימו לב באיזה ייצוג של הפונקציה הריבועית כדאי להשתמש.

ג. צפו במסלול קודקוד הפרבולה .

תארו מהו מסלול קודקוד הפרבולה כאשר משנים את הפרמטר b בתבנית. 
נמקו והוכיחו את השערתכם. 

ועוד פונקציות בתנועה:

כיתה רוקדת את ריקוד הפרבולות – צעדי הריקוד הם פונקציות! מאת איתן לירון.

ריקוד הפונקציות – מצגת מלווה במוסיקה בה צעדי ריקוד של פונקציות, מקור TES , רשת מורים אנגלית.

Angry birds - יישום המבוסס על המשחק הפופולרי. על התלמיד להתאים את הפונקציה הריבועית המתאימה למסלול.

המזרקה – יש להתאים פונקציה ריבועית לתמונה נתונה של פרבולות (כמזרקה), על ידי שינוי הפרמטרים בהצגה הקודקודית.  

לדמיין את המספרים המדומים

תקציר | לדמיין את המספרים המדומים |פתרון  | لنتخيّل الأعداد الخياليّة

בפעילות זו נחפש את הקשר בין השורשים המרוכבים של משוואה ריבועית לגרף הפרבולה שלה. היעזרו ביישום הדינאמי.

א. נתונה הפונקציה: 

1. מהם הפתרונות של המשוואה: ?
2. מהו קדקוד הפרבולה? מהו ציר הסימטריה?
3. תארו את מיקום השורשים הממשיים ביחס לציר הסימטריה והקדקוד.

ב.נתונה הפונקציה: .

1. מהם הפתרונות של המשוואה: ? כמה פתרונות ממשיים שונים? 
2. תארו את מיקום השורשים הממשיים ביחס לציר הסימטריה והקדקוד.

ג. נתונה הפונקציה: .

1. מהם הפתרונות הממשיים של המשוואה ? 
2. מהו ציר הסימטריה של הפרבולה? 
3. מצאו את השורשים המרוכבים של המשוואה.
4. תארו את מיקומם של השורשים המורכבים ביחס לציר הסימטריה והקדקוד.

ידוע לנו כי למשוואה ריבועית זו, אשר הפרבולה שלה "מרחפת", שני שורשים מרוכבים. אך השאלה היכן הם? ומדוע לא נוכל לראות אותם על הגרף? באופן מפתיע, אנו נמצא דרך פשוטה לאתר את השורשים בעזרת גרף הפרבולה וגרף נוסף שנקרא לו "האחות של הפרבולה". נזכור כי במישור המרוכב, ציר ה-x מייצג את החלק הממשי של המספר וציר ה-y מייצג את החלק המדומה.

ד. נתונה משפחת הפונקציות: .

1. הציגו ביישומון את שורשי המשוואה . מה ניתן לומר על שני השורשים המרוכבים ועל מיקומם ביחס לציר הסימטריה? 
2. שנו את הערך k ובדקו כיצד משתנים שורשי המשוואה. הביעו בעזרת k את שורשי המשוואה .
3.  שנו את הערך p ובדקו כיצד משתנים שורשי המשוואה. הביעו בעזרת p את שורשי המשוואה . 
4. הביעו בעזרת k ו-p את שורשי המשוואה . הוכיחו אלגברית.
5. הביעו בעזרת k ו-p את שורשי המשוואה . הוכיחו אלגברית.

ה. ניצור את גרף "האחות של הפרבולה" בעזרתו נאתר את מיקום השורשים המרוכבים.

שקפו את הפרבולה ביחס לישר y=4 וקבלו את גרף "האחות של הפרבולה". תארו את הגרף שלה ותנו ביטוי אלגברי למשוואתה.

ו. ניתן לומר על ארבעת השורשים של שתי הפרבולות האחיות?

ז. הסבירו את התהליך של מציאת השורשים המרוכבים ביחס לגרף הפרבולה, וחזרו על התהליך עבור המשוואה : .

ח. הביעו את שורשי המשוואה ואת שורשי משוואת הפרבולה האחות, בעזרת a,k,p. הוכיחו באופן אלגברי את הקשר בין השורשים.

מימדים – פרק 5 – מספרים מרוכבים

סרטון מרהיב, החמישי בסידרה "מימדים", בו מציג בפנינו המתמטיקאי הצרפתי אדריאן דואדי את הצד הגיאומטרי של המספרים המרוכבים, וכיצד ניתן לראות את המישור הממשי כישר מרוכב.

קישורים נוספים בנושא מספרים מרוכבים

• הצעת פתיחה לנושא מספרים מרוכבים – גילה רון. הצגה יצירתית וקצת אחרת של המספרים המרוכבים.
• בסיס אינטואיטיבי למשפט היסודי של האלגברה - מובשוביץ-הדר, זסלבסקי ושמוקלר, על"ה 16.
• בשביל מה אנחנו לומדים על מספרים מרוכבים ומה עושים עם זה? שלמה יונה
• מספרים מרוכבים - חוברת עזר בנושא מספרים מרוכבים שנכתבה על ידי שלמה מלמן
• כיצד נולדו המספרים? מצגת הסוקרת את ההתפתחות ההיסטורית המספרים עד להופעת המרוכבים.

יישומונים

• השורשים מסדר n
• פעולות שונות במספרים מכוונים בייצוג הגרפי –cut the knot
• Location of Complex Roots of a Real Quadratic – יישום של wolfram המציג את שורשי המשוואה הריבועית בתלת מימד.

סרטונים

• מורה פרטי 5 יח': מספרים מרוכבים א' – שיעור VOD מאת הטלוויזיה החינוכית
• מימדים – פרק 5 – מספרים מרוכבים
• המשוואה של בטמן - Batman Equation - Numberphile

המבוך של גלטון

תקציר| המבוך של גלטון|متاهة غالتون

בואו נשחק במשחק "המבוך של גלטון", או כפי שהוא מכונה גם מכונת גלטון. 
המשחק מורכב מלוח של מסמרים המסודרים כמשולש ב-7 שורות. זורקים כדור מראש הלוח, הכדור עושה דרכו מלמעלה עד למטה, כך שבכל פעם פוגע במסמר וממשיך את דרכו ימינה או שמאלה באופן אקראי וכך הלאה, עד שהוא מגיע לאחד התאים בתחתית הלוח.

1.א. באפשרותך להמר, ולבחור את התא הזוכה. הפעילו את הסימולציה והפילו כדור. (הנחיות) 
האם הכדור הגיע לתא שבחרת?

הפעילו את הסימולציה 10 פעמים, כמה כדורים פגעו בתא שבחרת?

הפעילו 100 פעמים, כמה כדורים פגעו בתא שבחרת? (ניתן להפיל את הכדורים באופן רציף ולעצור כש-n קרוב ל-100). לאיזה תא נכנסו רוב הכדורים?

שרטטו סקיצה של גרף העמודות ואפיינו את צורתו.

ב. נעם בחר בתא A₂ כמנצח. תארו מסלול אפשרי שבו הכדור נופל ל- A₂.

ג. השלימו לאיזה תא יגיע הכדור אם מסלולו יהיה:  

ד. הפעילו את הסימולציה 500 פעמים, והשלימו את טבלת השכיחויות על פי הניסוי: 

ה. שרטטו סקיצה לגרף העמודות ואפיינו את צורתו.

"זה החוק העליון של חוסר ההגיון. בכל פעם שיש כמות גדולה וכאוטית של נתונים, אתה מצעיד אותם לפי סדר הגודל שלהם ואז מופיעה, באופן מפתיע ויפהפה, צורה של סדר שהייתה סמויה לאורך כל הדרך"  Fransis Galton

2. כיצד נחשב את ההסתברויות השונות של הכדור הנופל בלוח גלטון?

א. נתבונן בלוח גלטון מוקטן , בעל שתי שורות בלבד. ברור שלכדור הנופל יש שתי אפשרויות בלבד בדרכו, שמאלה (L) או ימינה (R). מהי ההסתברות שיגיע לתא השמאלי?

ב. נוסיף שורה ללוח גלטון.

השלימו את תיאור המסלולים לכל תא.

בכמה מסלולים יכול הכדור להגיע לתא האמצעי?

מה מספר המסלולים האפשרי להגיע לכל אחד מהתאים בשורה השנייה?

מה ההסתברות שהכדור יפול לתא האמצעי?  

ג. מתואר עץ המתאים לכדור הנופל בלוח גלטון.

ד. רשמו על העץ, בכל תא את כל המסלולים של הכדור המגיע אליו. (L שמאל, R ימין)

ה. רשמו על העץ, בכל תא את מספר המסלולים האפשריים להגיע אליו.

ו. רשמו על העץ, בכל ענף את ההסתברות להגיע אליו.

3. המבוך של גלטון הוצב בשיפוע. כיצד ישתנה המשחק בו?

כיצד ישתנו ההסתברויות אם הסיכוי של הכדור ליפול ימינה גדול יותר מהסיכוי ליפול שמאלה....

התנסו במשחק בעזרת הסימולציה.

בחרו בלוח של 7 שורות ושנו את P.

א. כיצד ישתנה גרף העמודות? במה הוא שונה מגרף הפעמון שהכרנו קודם?

ב. מה ההסתברות שכדור יפול לתא A2, אם ההסתברות של כדור לפול שמאלה היא 0.6?

ג. מה ההסתברות שכדור יפול לתא A1, אם ההסתברות של כדור לפול שמאלה היא 0.6? ולתא A6? פרטו כיצד חישבתם.

ד. רשמו נוסחה להסתברות שכדור יפול בתא k בלוח גלטון של 7 שורות.

ה. רשמו נוסחה להסתברות שכדור יפול בתא k בלוח גלטון של n שורות.  

סרטונים

שני סרטוני הוראה של התפלגות בינומיאלית בעזרת כדור הנופל בלוח גלטון.

קישורים

לוח גלטון – יחידה אינטראקטיבית המלווה צעד אחר צעד את חישובי הסתברויות של נפילת כדור בלוח גלטון, התרשמות מגרף השכיחויות שבמספרים גדולים מתאר התפגות בינומית, עיסוק במשפט המספרים הגדולים ומשפט הגבול המרכזי.

יחידה מתוקשבת בנושא הסתברות למורים, הכוללת סרטים ויישומים אינטראקטיביים, ובה רקע על מדע ההסתברות, סקירה היסטורית, בחינת המשפט של המספרים הגדולים ומשפט הגבול המרכזי, חקר של משחקי מזל ויישומיהם והרחבה על מודל הסתברותי להבנת פקקי תנועה כמו גם שוק המניות. ביחידה חקר המשחק המבוך של גלטון כהמחשה של הנושאים הללו. מומלץ לצפות בהרצאה המסכמת.

יחידה מס 8: משולש פסקל, מצויינות ויצמן כוללת שתי חידות בשימוש עם מכונת גלטון.

יופיה של המתמטיקה – הסתברות, מצגת מאת גיל קלעי והרצאה מצולמת.

מוצג לא נורמי (או בעצם כן נורמלי)- פוסט מאת "אבא יש רק אחד", תיאור חוויתי במוזיאון המדע בבוסטון בו מוצג לוח גלטון.

יישום דינאמי של לוח גלטון מאת PHET

יישום דינאמי ללוח גלטון מאת math is fun.  

משולש פסקל בויקיפדיה

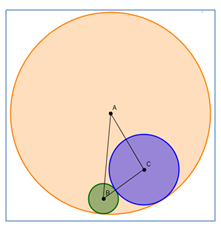
תקציר| מעגלים מתגלגלים| دوائر متدحرجة

1. דו-אופן ותלת אופן

שני מעגלים מתגלגלים בתוך מעגל גדול, משיקים כל העת זה לזה ולמעגל החוסם אותם. שני המעגלים הקטנים יותר, מרכזיהם B ו-C משיקים זה לזה חסומים בתוך מעגל גדול יותר שמרכזו A.

סובבו ביישומון את הנקודה B וחקרו את המעגלים המתגלגלים. 

א. האם וכיצד משתנה היקף המשולש ABC ? נמקו.

ב. מה היחס בין היקף המשולש לקוטר המעגל הגדול?

ג. אם נשנה את גודל המעגלים, כיצד ישתנה היקף המשולש ABC ? הסבירו.

ד. הוסיפו לשני המעגלים המתגלגלים מעגל נוסף שמרכזו בנקודה D. אם נשנה את גודל המעגלים כיצד ישתנה היקף המרובע ABCD? התנסו ביישומון.

2. המשולש המתגלגל

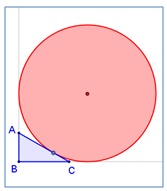
המשולש ABC חסום בין הקירות המאונכים והכדור המשיק לקירות.

חקרו ביישום הדינאמי כיצד משתנה היקף המשולש? למה הוא שווה?

3. כובע ליצן

כובע הליצן בנוי ממשולש שווה צלעות, בתוכו חסום עיגול קטן שרדיוסו 10 סנטימטר וחצי עיגול המשיק לעיגול הקטן ולצלעות המשולש.

א. מצאו מהו רדיוס חצי העיגול הגדול.

ב. מהו אורך צלע המשולש?

4. פרחים

סביב מרכז הפרח העגול מסודרים עלי הכותרת העגולים השווים בגודלם.

א. לפניכם שלושה פרחים: הפרח המשולש, הפרח המרובע, הפרח המשושה.

חשבו בכל פרח את היחס בין הרדיוס של המעגל הפנימי לבין רדיוס המעגל החיצוני.

העזרו ביישומון 

ב. למתקדמים (דרוש ידע בטריגונומטריה).

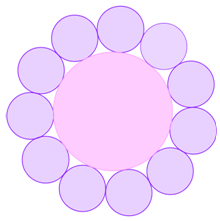לפניכם פרח עם 12 עלי כותרת. חשבו את היחס בין הרדיוס של המעגל הפנימי לבין רדיוס המעגל החיצוני.

ג. חשבו את היחס בין הרדיוס של המעגל הפנימי לבין רדיוס המעגל החיצוני בפרח בו n עלי כותרת.

הידעתם מה זה סנגקו (sangaku)?

במאה ה-17-19 שלטו השוגונים ביפן. היפנים חיו בניתוק מהמערב ולא נחשפו להתפתחויות המדעיות המערביות, אך התפתחה ופרחה מתמטיקה מקומית. מנהג עתיק היה לתלות תחת גגות של מקדשים וקברים, לוחות עץ צבעוניים עליהם צוירו בעיות גיאומטריות יפהפיות. לוחות אלו נקראו סנגקו, נתלו כאות הערכה ותודה לקדושים והזמינו את באי המקדש להתפלל וגם לפתור את החידות! לרוב בעיות ה sangaku יש סגנון מיוחד. הן מרבות לעסוק במעגלים, ריבועים, אליפסות, וכדורים במרחב, הנוגעים זה בזה. קראו עוד.

קישורים נוספים

פיצויחם בנושא מעגלים:

יישומים דינאמיים - משפטים ובעיות בנושא פאי, המעגל, בעיות עם מעגל

אוצרות פיתגורס – פיצוח ובו בעיות עם מעגלים משיקים ופתרונן בעזרת משפט פיתגורס.

חידת סנגקו בגאוגברה, וידאו המסביר כיצד לבנות בגאוגברה בתוך מעגל שלושה מעגלים משיקים זה לזה ומשיקים למעגל הגדול החוסם אותם.

בעיה הלקוחה מגיאומטריית המקדשים היפנית - אליהו לוי, הטכניון.

Japanese tample geometry -
,Tony Rothman , Scientific American May 1998 - מאמר המתאר את מסורת הסנגוקו, חידות גיאומטריות יפניות עם מעגלים וכדורים ואת פתרונן.

פלקסגון – קיפול ניר צבעוני עם חידות סנגוקו

התנהגות מתמטית בעלת גוון של שימור - שלמה חריר, משה סטופל, על"ה 35.

שרשרת שטיינר

 תקציר| מה לעז ולגיאומטריה?| ما للعنزة والهندسة؟

1. במרכז שדה ריבועי 5x5 מ"ר, קשורה בחבל עז רעבתנית, האוכלת כל עשב הנקרה בדרכה.

א. מה צריך להיות אורך החבל כך שתאכל רק חצי מהשדה? מהי צורת השטח שתאכל העז? 
התנסו ביישומון 

ב. מהו אורך החבל הגדול ביותר שניתן לקשור בשדה זה? איזה חלק של השדה תאכל אז העז?

2. בתוך שדה רחב נמצא שטח מרוצף ריבועי שאורך צלעו 2 מטר. אל קצות השטח קשורה עז בלולאה בחבל באורך 1 מטר. 
העז מסתובבת סביב השטח המגודר ואוכלת את כל העשב אליו היא מגיעה.

התנסו ביישומון,

הזיזו את הלולאה של החבל סביב, וענו:

א. מהי צורת השטח שתאכל העז? חשבו את השטח של העשב הנאכל. הסבירו.
ב. בשדה אחר העז הרעבתנית נקשרה לשטח בצורת מחומש משוכלל שאורך צלעו 2 מטרים. מהי צורת השטח שתאכל העז הפעם? חשבו את השטח של העשב הנאכל. הסבירו. 
ג. כיצד ישתנה השטח שתאכל העז אם השטח יהיה בצורת משושה משוכלל שאורך צלעו 2 מטרים? משולש שווה צלעות? 
ד. הכלילו מהי צורת השטח שתאכל העז סביב שטח בצורת מצולע משוכלל בעל n צלעות? הביעו את שטחו בעזרת n.

3. במרכז שדה נמצא שטח מגודר מלבני ומרוצף בגודל 4x6 מ"ר. עז רעבתנית קשורה האחת הנקודות על הצלע CD. 
נסו לשער בכל אחד מהמקרים הבאים את צורת השטח שתאכל העז ואת שטחה. 
בדקו ביישומון.

א. העז קשורה אל הקודקוד C בחבל שאורכו 3 מטרים, 4 מטרים, 5 מטרים, 10 מטרים. 
ב. העז קשורה אל אמצע הצלע CD בחבל שאורכו 3 מטרים, 4 מטרים, 5 מטרים, 10 מטרים. 
ג. היכן לדעתכם נקשרה העז, אם צורת השדה שהתקבלה כבאיור הבא. 
ד. אורך החבל 10 מטרים, היכן יש לקשור את העז על הצלע CD, כך שיתקבל שטח מקסימלי?

תקציר| דמיון ברחבי העולם| פתרונות| בערבית 

1. הפירמידה במצריים

תאלס היה פילוסוף ומתמטיקאי יווני, מהמאה ה-7 לפנה"ס. תאלס היה הראשון שראה את הצורך בחשיבה דדוקטיבית וחקר את רעיון ההוכחות הגיאומטריות. הוא מפורסם בשני משפטים גיאומטריים שנקראו על שמו, משפטי תאלס, האחד קשור לדמיון והשני למעגל.

הפירמידה הגדולה בגיזה שבמצריים, הידועה גם בשם הפירמידה של ח'ופו, הפרעה שבנה אותה, היא אחת משבעת פלאי תבל. רבים ניסו בעת העתיקה לאמוד את גובהה ללא הצלחה, אך תאלס (600 לפנה"ס) חישב את גובהה של הפירמידה באמצעים פשוטים ובעזרת הידע המתמטי שלו.

נשכב על החול ביום שמש ליד הפירמידה ובקש שיסמנו בחול את גובהו. לאחר שסמנו את גובהו בחול הוא נעמד בתחילת הסימון כך שגופו יצר צל לאורך הסימון על החול ומעבר לסימון. באותו זמן יצרה הפירמידה אותה ביקש למדוד צל משלה.

תאלס אמר לנלווים אליו:
"כאשר צילי יגיע לגובהי המסומן, מדדו את צל הפירמידה."

הם מדדו ומצאו שאורך צל הפירמידה 145 מ'. מה גובה הפירמידה? 

הסבירו את שיטת מדידתו של תאלס. 

2. בעית המיתרים של בסקרה – הודו

בסקרה (Bhaskra) אסטרונום ומתמטיקאי הודי מהמאה ה-12. מפורסם בפיתוח שיטות לפתרון משוואות ריבועיות ועוד, חיבר כללים לפעולות במספרים חיוביים ושליליים ואף הציג שתי הוכחות יפות ופשוטות למשפט פיתגורס בעזרת דמיון משולשים. 

בין שני עמודים בגובה 15 מטר ו-10 מטר,נמתחו מיתרים באלכסון. בנקודת המפגש בין המיתרים הוצב עמוד תומך. 
לא ידוע המרחק בין העמודים.

ג. אם ידוע שגובה שני העמודים a ו-b. הביעו באמצעות a ו-b את גובה העמוד התומך.  

3. התעלה בסאמוס (יוון)

באי סאמוס היפהפה שביוון העתיקה (הידועה כיום בשם פיתגוריה..), בעיר הנמל החשובה לא היו מספיק מים לתושבים ולצבא, אך היה שפע של מים בהרים. בשנת 530 לפנה"ס, נחפרה תעלה באורך של קילומטר דרך ליבו של הר אבן קשה (ההר קסטרו). שני צוותי חפירה התקדמו זה מול זה משני קצות התעלה והצליחו להיפגש באמצע כמעט ללא טעות. החופרים השתמשו בפטישים ואיזמלים בלבד, ולא היה ברשותם מצפן, מפה טופוגרפית או כל מכשיר ניווט אחר. זוהי משימה מאתגרת גם כיום עם יכולות הטכנולוגיה המודרנית. מהנדס חפירת התעלה, יאופלינוס (Eupalinos) השתמש בתכנון אך ורק בגיאומטריה ובפתרון פשוט ומפתיע הצליח לתת לשני צוותי החפירה את הזווית המדויקת בה יחפרו. כיצד עשה זאת?

הבעיה שהתמודד איתה אופלינוס היה לקבוע את הכוון של כל צוות חפירה. לשם כך ערך סיור רגלי מסביב לאי בין המעין שבהר עד לעיר הנמל בקצה השני, כשהוא הולך בקווים ישרים ואנכים זה לזה. הוא מדד את אורכי קטעי המסלול שלו, וכך הצליח לדמיין משולש ישר זווית עם הזווית המבוקשת.

א.   מה מתאר סכום הניצבים האנכיים?

ב.   כיצד ניתן למדוד את הניצב האופקי של המשולש?

ג.   כיצד קבעו היוונים זווית ישרה?

      יש הסוברים שהשתמשו בשני מקלות באורכים שווים וסימון האמצע של כל אחד מהם.
      הסבירו כיצד עובדת השיטה?

הרחבה:
השיטה המצרית למשולש ישר זווית: משולש מצרי (בעיה 4 בפיצוח קיפולי נייר גיאומטריים)

4. דמיון בסין

ראשית נכיר את עקרון "משני הצדדים". 

א. הנקודה E היא נקודה כלשהי על אלכסון המלבן ABCD. מעבירים מהנקודה E קטעים המקבילים לצלעות המלבן.
מה הקשר בין שטחי שני המלבנים שנוצרו (DHEG  ו- FEIB )? 
הזיזו את הנקודה E ביישומון, בדקו והוכיחו השערתכם.

ב. הראו כי המשולשים  ΔAFE~ΔEIC

ג. השתמשו בעקרון "משני הצדדים" (שוויון השטחים) בכדי לחשב את היחס a/b באמצעות h₁ ו-h₂.

ד. פתחו את עקרון "משני הצדדים" גם עבור מקבילית. 
    הראו כי המשולשים ΔAFE~ΔEIC דומים, וחשבו את היחס a/b באמצעות h₁ ו-h₂.
    נסחו משפט לגבי יחס הגבהים במשולשים דומים.

תוכלו להיעזר ביישומון. 

5. להשקיף על אי בים – סין

המתמטיקה הסינית שימשה את מהנדסי האימפריה הסינית במדידות של שטחי שדות, בהכנת לוח השנה, לצרכים צבאיים, נווט וכדומה. המתמטיקאי הסיני ליו הואי, בן המאה ה-3, כתב את הספר "תשעת הפרקים של אמנות המתמטיקה", ובאחד הפרקים כתב מדריך מתמטי לאי בים, הכולל בעיות שונות בנווט ופתרונן המתמטי.

כיצד נמדוד את גובהו של צוק הררי בלב ים ?
ליו הואי פיתח שיטה הנקראת "הפרש כפול" למדידת עצם רחוק מבלי להגיע אליו, בעזרת עקרון "הפנים חוץ".

"העמדתי שני מוטות באורך 3 מטרים במרחק של 1000 צעדים זה מזה, כך שיהיו בקו ישר עם האי. הלכתי אחורה 123 צעדים מהמוט הראשון עד שראיתי את קצה המוט וקצה הסלע בקו אחד. כך גם צעדתי 127 צעדים מהמוט השני. כך הצלחתי למדוד את הגובה של הסלע באי ומרחקו מהמוט. "

התוכלו גם אתם למדוד את גובה הסלע?

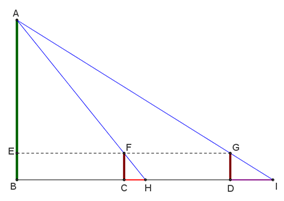א.  השלימו את משולש AHI למקבילית. העבירו מהנקודה G שעל אלכסון המקבילית, מקבילים לצלעות. סמנו את המשולשים הדומים שהתקבלו.

ב.  חשבו את אורכי צלעות המשולשים בעזרת הפרשי האורכים הנתונים. היעזרו ביישומון

ג.  חשבו בעזרת עקרון "משני הצדדים" את גובה הסלע AB.

ד.  הכלילו את השיטה.

מקורות נוספים:

• ההנדסה של האימפריה, סרט של ערוץ ההיסטוריה על בניית תעלת סאמוס. (בערך 7 דקות)

פיצוחים בנושא דמיון: 

• פרויקט עולמי למדידת היקף כדור הארץ
• ממוצעי פיתגורס ועוד
• על כנפי הדמיון
• אני דומה לעצמי