תקציר| זהו את הזהות הטריגונומטרית| פתרונות| ميّزوا المتطابقات المثلثية| حلول

1. זהויות טריגונומטריות לסכום זוויות

באיור הבא נתון DB=1.

א. איזה קטע באיור שווה ל- (sin(α+β ?   

    איזה קטע באיור שווה ל- (cos(α+β ? 

ב. שנו באיור הדינאמי את הזווית α באמצעות הקודקוד A,     

    כך שסכום הזוויות α+β  נשאר קבוע.   

    אילו גדלים משתנים באיור ואילו נשמרים? 

    האם מתקיים sin(α+β)=sinα+sinβ ?

    האם מתקיים cos(α+β)=cosα+cosβ ?

ג. שנו באיור הדינאמי את הזווית β באמצעות הקודקוד B,   

    כך שסכום הזוויות α+β למעשה משתנה.

    אילו גדלים משתנים באיור ואילו נשמרים? 

    האם מתקיים sin(α+β)=sinα+sinβ ?

    האם מתקיים cos(α+β)=cosα+cosβ ?

*  אילו זוויות α, β מקיימות sin(α+β)=sinα+sinβ ?

   ברצוננו להביע את (sin(α+β באמצעות sinα ו- sinβ בלבד. 

ד. הביעו את אורכי הקטעים:

GH, BF, HF, DG, DH, BH באמצעות β,α בלבד.      

ה. רשמו נוסחאות מתאימות:

_________________ = (sin(α+β

_________________ = (cos(α+β

ו. רשמו נוסחאות מתאימות לזווית כפולה:

_________________ = (sin(2α

_________________ = (cos(2β

מקור: הוכחות ויזואליות: השקפותיהם ואמונותיהם של התלמידים, רז הראל טומי דרייפוס, על"ה 41

2. זהויות טריגונומטריות לזווית כפולה

א. הסבירו מדוע זווית AOB> כפולה מזווית BAM>  

ב. עקבו באיור הדינאמי אחר השתנות הזוויות וערכי הסינוס שלהן. 

ג. הביעו את AM בשתי דרכים:

    1) בעזרת משולש ΔAOM  

    2) בעזרת משולש ΔABM 

    מה ניתן להסיק?  

ג. כיצד תוכיחו את הנוסחה כאשר הזווית AOB> קהה?

ד. הביעו את OM בשתי דרכים. מה תוכלו להסיק הפעם? 

מקור: NRICH

3. עוד זהויות טריגונומטריות לזווית כפולה 

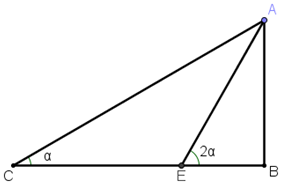
באיור הבא נתון CB=2.

נסמן t=tanα.

הביעו את אורכי צלעות המשולשים באיור באמצעות t.

הוכיחו באמצעות האיור את הזהויות הטריגונומטריות הבאות לזווית כפולה:

4. זהויות טריגונומטריות מפתיעות 

ידועה הנוסחה: 

נסמן tanα=t. הוכיחו את הזהויות ושימו לב לתופעה המפתיעה:

מה נקבל אם נרשום ממול כל אחד מהזהויות את המקדמים של t מהמונה ומהמכנה בסדר עולה?

מהי הנוסחה ל- (tan(5α?  ל- (tan(nα?

זהויות טריגונומטריות בשילוב גישת "מה אם לא?" - גילה רון, אורית זסלבסקי, קשר חם.

משחקים ודפי עבודה לתרגול בטריגונומטריה - NCTM

תקציר|אני דומה לעצמי?|أنا اشبه نفسي

הכירו את הפקרטל המפורסם, משולש סרפינסקי.

משולש סרפינסקי נוצר בסדרה אינסופית של משולשים

הדומים לעצמם בכל רמת פירוט שנסתכל בה.

לתכונה זו קוראים,  "דמיון עצמי" ,כלומר כל חלק של הפרקטל נראה כמו השלם, החלק של החלק נראה כמו החלק וכך הלאה....

1. עקבו אחר התפתחות הפרקטל של משולש סרפינסקי, ביישומון הפרקטל  או בתמונה למטה:

א. תארו כיצד בכל שלב תמונת המשולש משתנה. 

    מה משתנה במעבר משלב לשלב, ומה נשאר קבוע?

ב. מצאו חוקיות בסדרה ותארו אותה.

ג. התבוננו בשלב השני ומצאו זוגות של משולשים דומים (שאינם זהים)? מהו יחס הדמיון בכל זוג?

    אילו משולשים דומים ניתן למצוא בשלב השלישי? מהו יחס הדמיון בכל זוג?

    תארו את בניית משולש סרפינסקי בעזרת משולשים דומים.

ד. כמה משולשים ירוקים בשלב השלישי? כמה יהיו בשלב הרביעי? כמה יהיו בשלב ה- n?

ה. כמה משולשים לבנים בשלב השלישי? כמה יהיו בשלב הרביעי? כמה יהיו בשלב ה- n?

ו. נניח בשלב התחילי שטח המשולש הירוק הוא 1 יחידה רבועה.

   מהו שטח המשולשים הירוקים בשלב הראשון? השני? השלישי? 

   התוכלו להעריך את שטח המשולשים הירוקים בשלב ה-100? בשלב ה- n?

2. ניתן לעצב פרקטלים מרהיבים בצורות שונות שלהם תכונת הדמיון העצמי. 

האם תוכלו לבנות סדרה בחוקיות דומה בריבועים? נסו לציירה ולמצוא את יחס הדמיון בה.

אם תתבוננו מסביבכם תמצאו פרקטלים רבים בטבע:

עצים וענפים, הכרובית והברוקולי, פתית השלג, צדפים, הברקים וסופות הוריקן ועוד.

מנדלברוט (1924-2010), מתמטיקאי יהודי, היה  הוגה רעיון הפרקטלים. הראה, שתכונת הדמיון העצמי איננה גחמה מתמטית של גיאומטריה. היכולת להמשיך סדרות כאלו עד אין סוף התגלתה הודות ליכולתם של מחשבים מודרניים לבצע מיליארדי פעולות בשנייה, אבל היא קיימת בטבע, באוויר, בים וביבשה.

Where do we find fractals? - פוסטר מאת Fractal Foundation

3. לפניכם פרקטל ריבועי נוסף מתוך יישומון הפרקטל :

א. תארו כיצד בכל שלב תמונת הריבוע משתנה.

    מה משתנה במעבר משלב לשלב, ומה נשאר קבוע?

ב. מצאו חוקיות בסדרה ותארו אותה.

ג. התבוננו בשלב השני ומצאו זוגות של רבועים דומים (שאינם זהים)? מהו יחס הדמיון בכל זוג?

    אילו מרובעים דומים ניתן למצוא בשלב השלישי? מהו יחס הדמיון בכל זוג?

ד. כמה ריבועים מכל צבע בשלב השני? השלישי? כמה יהיו בשלב הרביעי? כמה יהיו בשלב ה- n?

ה. נניח בשלב התחילי (שלב אפס) הוא 1 יחידה רבועה.

    מהו שטח הריבוע הכתום בשלב הראשון? בשלב השני? השלישי? בשלב ה- n?

ו. נניח בשלב התחילי שטח הריבוע הכתום הוא 1 יחידה רבועה.

   מהו שטח הריבועים הכחולים בשלב הראשון? השני? השלישי? בשלב ה- n?

קראו עוד על פרקטלים:

לחיות עם אי הודאות - צבי ינאי, מדור מדע ב-YNET.

פרקטלים ומשולש סרפינסקי וחקר השברים (עמ' 4-6) - מרכז ארצי למורים למתמטיקה בחינוך היסודי

משחקים כסביבה להצגת מושגים ומשפטים מתמטיים ולפתרון בעיות, חלק ב' - נצה מובשוביץ הדר, על"ה 41.

תוכלו לקרוא על המימדים של פרקטל- מאמר מאת NRICH

Ron Eglash on African fractals | Video on TED.com - הרצאת וידאו (אנגלית עם תרגום לעברית) - מומלץ

תקציר|אני ואתה נשנה את העולם |פתרונות|أنا وأنت نغيّر العالم

זוכרים את הסרט "תעביר את זה הלאה" ("Pay It Forward")?  זוהי דרמה המבוססת על הספר המצליח של קתרין ריאן הייד. הסרט יצא בשנת 2000 וגרם לאנשים רבים שצפו בו לפעול ברוח הרעיון, לתרום לחברה ולהאמין כי "אני ואתה נשנה את העולם".

טרוור הוא ילד ממשפחה קשת יום שחי בלאס וגאס. כאשר הוא מגיע לכיתה ז' בבית הספר הוא מקבל מהמורה שלו משימה לימודית - לנסות ולמצוא דרך שתשנה את העולם.

צפו בסרט אחר הרעיון הקטן של טרוור שיכול לעשות שנוי גדול:

"אני אעשה משהו טוב עבור שלושה אנשים. וכשהם ישאלו כיצד הם יגמלו לי בעבור זה, אני אומר להם תעבירו את זה הלאה... כל אחד מכם יעביר לעוד שלושה אנשים. כך יוצא שתשעה אנשים נוספים יצטרכו לעשות מעשה טוב לעוד עשרים ושבעה! ואז תנסו לחשב... אתם רואים כמה גדול זה יוצא?"

נניח כי בכל יום "מעבירים את זה הלאה".

1. מה תוכלו לומר על הגידול של מספר האנשים שמעבירים את זה הלאה ככל שהימים חולפים?  
    התוכלו לנחש כמה אנשים יעבירו מעשה טוב ביום ה-6 ? 

    התוכלו לנחש באיזה יום יותר מ-1000 אנשים נוספים יעבירו מעשה טוב הלאה? 

    כעת נחשב "כמה גדול זה יוצא?" - השלימו את הטבלה את הדינאמית (אקסל), וסמנו נקודות מתאימות במערכת הצירים.

 הערה- תוכלו להיעזר במילוי הטבלה בגיליון האלקטרוני בנוסחה והעתקתה. (בכל שלב גדול מספר האנשים שקיבלו להעביר הלאה פי שלוש מהשלב הקודם) 

2. המבצע שיזם טרוור "להעביר את זה הלאה" עבד שישה ימים.

    כמה אנשים נוספים עשו מעשה טוב ביום השישי? 

    מה מספר המעשים הטובים שנעשו במבצע "העבירו הלאה" במהלך ששת הימים?

3. המבצע "להעביר את זה הלאה" עבד n ימים.

    כמה אנשים נוספים עשו מעשה טוב ביום ה-n?

    מה מספר המעשים הטובים שנעשו במבצע "העבירו הלאה" במהלך n הימים?

4. באיזה יום מתחילת המבצע כל תלמידי הכיתה שלכם "יעבירו את זה הלאה" לאחרים?

     כמה ימים דרושים כדי שכל תלמידי בית הספר שלכם "יעבירו את זה הלאה" לאחרים?

     האם ניתן להעריך זאת מתוך הנקודות שסימנתם במערכת הצירים?

5. התבוננו במערכת הצירים בגרף שיצרתם. האם כדאי לחבר את הנקודות שעל הגרף?

    האם תוכלו למצוא נקודה בה x=6.5 ? מה המשמעות של נקודה זו?

    כיצד לדעתכם נראה הגרף של מבצע "העבר את זה הלאה"?

6. חשבו כמה זמן ייקח עד ש-1000 אנשים בדיוק יעבירו הלאה מעשה טוב לאחרים.

7. כיום יש במדינת ישראל כ- 7,500,000‏‏‏ תושבים. 

    כמה ימים דרושים כדי שכל תושבי מדינת ישראל ייטלו חלק במבצע?

8. כיצד היה משתנה אופן גידול האנשים אם טרוור היה מציע "להעביר הלאה" בכל יום לאיש נוסף אחד בלבד? 

    כיצד הייתה משתנים הגרף והחוקיות?

9. כיצד תשתנה החוקיות אם מעבירים הלאה בכל יום לשני אנשים נוספים? 

    לשלושה, לארבעה אנשים נוספים?

    התאימו גרף לכל מקרה.

10. לקראת פורים, בית הספר "חופים", בו 1000 תלמידים, פתח במבצע של משלוחי מנות. 

        על כל תלמיד לשלוח לשלושה אנשים משלוח מנות. וכל אחד מהם עליו לשלוח משלוח מנות לשלושה אנשים נוספים.

        תוך כמה צעדים במבצע יקבלו יותר ממיליון אנשים משלוח מנות?

        כיצד תשתנה החוקיות? כיצד ישתנה הגרף?

פרוייקט "תעביר את זה הלאה" בשפת הסימנים

זהו פרוייקט חברתי-התנדבותי ליצירת מודעות, גישור ואיחוד בין הקהילה ה'שומעת' והקהילה ה'חירשת' בישראל. למד את שפת הסימנים והעבר את הידע שלך הלאה, כך נרחיב את קהילת דוברי שפת הסימנים.

"תעביר את זה הלאה" - פרוייקטים קהילתיים

המקום בו נפגשים אנשים טובים כדי לעשות מעשים טובים.

פינג-פונג מתמטי - על"ה 38, תשס"ז 2007, רון אהרוני, גילוי נוסחא לסכום של סדרה גיאומטרית.

תקציר|שעשועי משולשים |פתרונות|تسالي مثلثات|حلول

1. אתגר המשולשים 

באיור מתואר דגם של משולשים הבנויים מגפרורים.

כמה משולשים (מכל גודל) בסה"כ באיור?

התוכלו להוריד שני גפרורים מהמבנה המשולש הבא כדי שיהיו בו שני משולשים בלבד.

2. משולש המשולשים 

באיור מתואר דגם של משולש המשולשים הבנויים מגפרורים.

1) בניית משולש המשולשים הבנוי מגפרורים
     א. מכמה גפרורים בנוי הדגם?
     ב. הוסיפו לדגם שורה של משולשים, כמה גפרורים נוספו?
         כמה גפרורים יש בדגם כעת?
     ג. התוכלו למצוא את החוקיות למספר הגפרורים בדגם בו n שורות.

2) המשולשים הקטנים
     התבוננו במשולשים הקטנים במשולש המשולשים.
     א. כמה משולשים קטנים בדגם? 
     ב. איזה חלק מהווה כל משולש קטן מהמשולש הגדול?
     ג. הוסיפו לדגם שורה של משולשים, כמה משולשים קטנים נוספו?
        כמה משולשים קטנים יש בדגם כעת?
     ד. התוכלו למצוא את החוקיות למספר המשולשים הקטנים בדגם בו n שורות.

3) המשולשים כולם

     במשולש המשולשים ניתן למצוא משולשים שווי צלעות מגדלים שונים.

     א. כמה משולשים שווי צלעות (מכל גודל) בסה"כ באיור?

         תוכלו להיעזר בספירה בסרטון הקצר הבא.

      ב. הוסיפו לדגם שורה של משולשים, כמה משולשים שווי צלעות (מכל גודל) יש בדגם כעת?

      ג. התוכלו למצוא את החוקיות למספר המשולשים בדגם בו n שורות.

3. גזרו עוד ועוד משולשים 

באיור משולש שווה צלעות שניתן לגזור אותו לארבעה משולשים קטנים יותר.

א. הראו כיצד ניתן לגזור את המשולש ל- 9 משולשים

    שווי צלעות קטנים יותר. כיצד ניתן לחתוך ל- 16 משולשים?

    מהי מסקנתכם?

ב. כיצד ניתן לגזור את המשולש ל-6 משולשים שווי צלעות?

    רמז - המשולשים לא בהכרח באותו גודל.

ג. דנה גזרה את המשולש הגדול באופן המתואר באיור.

   כמה משולשים שווי צלעות נוצרו בחיתוך?

ד. התוכלו לגזור באופן דומה את המשולש ל- 8 משולשים?

   הראו כי ניתן לגזור את המשולש לכל מספר זוגי של משולשים.

ה. הציעו דרך לגזור את המשולש שווה הצלעות ל-7 משולשים שווי צלעות. ל-11 משולשים?

ו. אתגר- האם ניתן לחתוך משולשים שווי צלעות לכל מספר של משולשים?

מקורות נוספים:

כיצד מחלקים משולש? , פרופ' שמואל אביטל, גליונות לחשבון מס' 50 .

חפיפה בגן היתכן?, בעיית החודש 22, קשר ח"ם.

גיאומטריה של מגן דוד, בעיית החודש 5, קשר ח"ם.

קסמי משולשים - חידה מאלף אפס

תקציר|הרהורים על התחלקות |פתרונות|تفكير في القسمة |تفكير في القسمة _ حلول.

המשפט הקטן של פרמה לכל p  ראשוני  n^p)-n)  מתחלק ב- p.

פרמה (1665-1601) כהרגלו לא הציג את הוכחת המשפט.

אויילר אחריו הביא שתי הוכחות, אחת המבוססת על התכונות של מקדמי הבינום והשנייה על תכונות של שאריות. 

לפניכם הוכחה באינדוקציה, מתוך אלף אפס.

קראו גם על המשפט הגדול (האחרון) של פרמה.

א. הסבירו ע"פ האיור, או בדרך אחרת, מדוע עבור כל n טבעי n²)-n) מתחלק ב- 2.

ב. התבוננו בסרטון של בניית הקובייה. כמה חלקים מכל סוג בנויה הקובייה 3x3x3: 
 

הסבירו כיצד ניתן להסיק מבניית הקובייה כי 3-(3³) מתחלק ב- 3. 

האם הביטוי מתחלק גם ב-6?

דמיינו בניית קוביית nxnxn.  
תארו את חלקי הקובייה והסבירו מדוע  לכל  n טבעי,  n³)-n) מתחלק ב- 3.
הראו כי הביטוי מתחלק גם ב-6. 

ג. דן טען שהוא יוכיח את טענה זו בעזרת פירוק לגורמים.

 (n³)-n = n.( (n²) - 1) = n(n-1)(n+1)    

מה ניתן לומר על שלושת הגורמים של הביטוי? 

מה ניתן להסיק מהפירוק לגורמים?

ד. דנה המשיכה וטענה כי באופן דומה, בעזרת פירוק לגורמים, אפשר להוכיח טענות נוספות כגון:

         1). לכל n טבעי,  n⁵) - n) מתחלק ב- 6.

         2). לכל n טבעי,  n⁵) - n)  מתחלק ב- 5. 
                    רמז- בדקו את כל האפשרויות לספרה האחרונה של המספר n.

         3). לכל n טבעי,  n⁵) - n)  מתחלק ב- 30.

ה. דן ודנה בדקו מקרים שונים של המשפט הקטן של פרמה.

הם ביקשו להראות כי (11¹⁰) - 10 מתחלק ב- 11.

המורה הציעה להם להיעזר בנוסחאות הפירוק לפי הבינום של ניוטון (מצורפות מטה) .

הכיצד?

ו. "אם כך.." אמר דן ניתן להסיק כי: " 999,9999,999 מתחלק ב-11" בדקו.

דנה מיד הוסיפה: "אז גם  999,999 מתחלק ב-7 ". ". בדקו.

דן ודנה נסחו טענה חדשה יחד: 

לכל מספר ראשוני אפשר להתאים מספר שכולו תשיעיות המתחלק בראשוני זה. מה דעתכם?

דנה חשב כמעה והוסיף , "ראה המשפט אינו נכון כאשר n=2  ו- n=5". מדוע?

התוכלו לתקן את המשפט?

נוסחאות פירוק ע"פ נוסחת הבינום של ניוטון

 פירמידה שכזו 

שימו לב לעובדה המפתיעה בפירמידה שלפנינו:

בכל שורה מספר המתחלק ב-11.

11:11 =1

1001:11=91

100001:11=9091

10000001:11=909091

כלומר המספר 10 בחזקת n ועוד 1, כאשר n טבעי אי זוגי , מתחלק ב-11.

הוכיחו בעזרת אחד נוסחאות הפירוק שבטבלה מעלה.

אחד עשר מי יודע?

א. בחרו מספר בן ארבע ספרות, חברו לו את המספר בסדר ספרות הפוך.
האם קיבלתם מספר המתחלק ב- 11? הכיצד?

ב. בחרו מספר בעל מספר זוגי של ספרות, חברו לו את המספר בסדר ספרות הפוך.
האם גם הפעם קיבלתם מספר המתחלק ב- 11? הכיצד?

ג. בחרו מספר דו ספרתי והצמידו לו את המספר בסדר ספרות הפוך. 
קיבלתם מספר פלינדרום ארבע ספרתי (abba) האם גם הוא מתחלק ב- 11?

ד. האם כל מספר פלינדרום עם מספר זוגי של ספרות מתחלק ב-11?

     
 קראו עוד: מבחן החלוקה ב-11 - אורט בראודה             קראו עוד: יבין ניבי- על פלינדרומים ועל מספרים פלינדרומים,

                                                                                 ד"ר זיווה דויטש, עקיבא קדרי, אלף אפס

מקורות נוספים:

עזרי לימוד להמחשה של מקרה פרטי של המשפט הקטן של פרמה, דן בן שאול, על"ה 35

תגובה למאמר "הוכחה בדרך אחרת", מרק אפלבאום, על"ה 35

9, 99, 999 ומספרים פלינדרומים, יפים כץ, על"ה 34

הוכחה בדרך אחרת, פתחי סלאח, על"ה 31

מה מבינים תלמידנו במושג האינדוקציה, יונתן אחיטוב, על"ה  29

החשבון המודולארי בשירות האינדוקציה, עופר ליבה, על"ה 20

פלינדרום אצל אבן עזרא - קלרה זיסקין, על"ה 33            

הלוך ושוב, בעיית החודש 6, קשר ח"ם               

סימני התחלקות א, סימני התחלקות ב' , ד"ר מריטה ברבש, מכללת אחווה

בעיות נוספות בנושא:

הוכחת משפטי התחלקות (ללא אינדוקציה) - ליקטה, יצרה וערכה קלרה זיסקין.

בעיות יפות בהתחלקות - ליקטה, יצרה וערכה קלרה זיסקין.

תקציר|יום כדור הארץ|פתרונות|יום כדור הארץ בערבית|حلول

כמה עצים צריך לשתול בשנה בכדי לפצות על זיהום האוויר שיוצרת מכונית משפחתית אחת?

ראשית, שאלו את הוריכם על המכונית המשפחתית שלכם: 

א. כמה קילומטרים בשנה נוסעת המכונית? (למשל, 20,000 ק"מ).

ב. כמה ליטרים של דלק צורכת המכונית בממוצע לכל קילומטר? (למשל 12 ק"מ ליטר). 

כעת לחישובים:  

א. חשבו כמה ליטרים של דלק צורכת מכוניתכם בשנה?

ב. מכונית ממוצעת פולטת לכל ליטר של דלק כ-2.36 ק"ג פחמן דו חמצני (CO2 ).
    חשבו כמה פחמן פולטת מכוניתכם בשנה?

ג. ידוע כי 1000 עצים סופגים 20,000 ק"ג פחמן דו חמצני.
    כמה עצים יש לשתול בכדי שיפצו על פליטת הפחמן של מכוניתכם?

ד. בישראל כל שנה מיובאות כ- 150,000 מכוניות חדשות.
    כמה עצים יש לשתול בכדי למנוע את זהום האוויר שהן עלולות לגרום?

ולמעשים: 

הציעו דרכים כיצד ניתן להפחית את זיהום האוויר ממכוניות?

שמעתם על  "אפקט הפרפר"?

מדען בשם אדוארד לורנץ שחקר את תופעות מזג האוויר, הגה את רעיון אפקט הפרפר. טען שרפרוף כנפיים של פרפר במקום אחד בעולם יכול לגרום לסערה במקום אחר, מרוחק ממנו. כלומר, שינוי קטן באטמוספרה במקום אחד יכול לגרום לשרשרת

של שינויים שיתפתחו ויגדלו לסערה ענקית הרחק הרחק מהמקום שהשינוי החל בו.

הֱיו גם אתם פרפרים - עשו דבר קטן במקום שאתם גרים בו, ויחד עם עוד פרפרים כמותכם, 

ילדים ומבוגרים שהסביבה יקרה להם חוללו שינוי:  

מקור: סבבה, האתר לאיכות הסביבה

תקציר|ערכים ומתמטיקה|פתרונות|تعاون ورياضيات|حلول - قيم ورياضيات

1. חברות ומתמטיקה

בעוד שבוע יערך בבית הספר מבחן מסכם במתמטיקה בכיתה ז'. רעות ועמית החליטו להתכונן יחד ולפתור 10 בעיות מתמטיות בכל יום.  

אך לרוע המזל, עמית חלתה והחסירה שבועיים של לימודים. כשחזרה היא התקשתה להשתלב בשעורי המתמטיקה ולעמוד במשימה.

ביום הראשון היא הצליחה לפתור רק בעיה אחת ואילו רעות הצליחה לפתור 10 בעיות.

נותרו עוד 6 ימים בלבד למבחן. רעות התגייסה לעזרתה של עמית ועזרה לה בשעות אחה"צ להשלים את החומר.

בימים הבאים, רעות המשיכה ופתרה 10 בעיות ביום ועמית הצליחה לפתור בכל יום 2 בעיות יותר מאשר ביום שלפני.

א. האם לדעתכם תצליח עמית לעמוד במשימה ולאחר 6 ימים תפתור 10 בעיות?

ב. הכינו טבלאות ערכים עבור מספר השאלות במתמטיקה שפתרה עמית ופתרה רעות.

ג. שרטטו במערכת צירים אחת גרף מתאים לכל אחת מהם.

ד. מהו הייצוג האלגברי של הפונקציות המתארות את מספר השאלות במתמטיקה שפתרה כל אחת מהתלמידות כתלות במספר השיעורים?

ה. בדקו ביישום הדינאמי את השרטוט שלכם ואת משוואות הישרים. 

תוכלו לשנות בסרגל את מספר הימים ולעקוב אחר התקדמותה של עמית לעומת רעות. 

באיזה יום עמית תצליח לפתור יותר שאלות מרעות?

ו. האם יש יום שבו פתרו השתים אותו מספר שאלות במתמטיקה? חברו משוואה המתארת מצב זה ופתרו אותה. מה משמעות הפתרון שקבלתם? כיצד בא לידי ביטוי פתרון זה באופן גרפי?

ז. תארו מקרה שבו נעזרתם בחבר/ה לכיתה כדי להשלים חומר שהחסירו. האם קיבלתם גמול בעבור עזרתכם? אם כן, מהו?

ח. תארו מקרה שבו עזרת לחברה/ה בכיתה כדי להשלים חומר. האם הצלחת במשימה? מה היה הגמול לעזרה שנתת?

2. שיעורי עזר 

רועי, עמית ונעם שלושה חברים טובים תלמידי כיתה ט, תכננו לצאת לטיול משותף בשביל ישראל. 

הם תכננו לחסוך יחד ולממן בעצמם את עלות הטיול, שהיא 500 ₪, באמצעות שיעורים פרטיים במתמטיקה לתלמידי כיתות ז'.

הם החליטו שהתשלום עבור שיעורי העזר יכלול מחיר התחלתי חד פעמי עבור עזרה בהפסקות ומחיר קבוע לכל שיעור שיתקיים. 

בכדי לעודד את הצלחת התלמידים והתמדתם הם חשבו לארגן טיול יומי עבורם בשביל ישראל בסביבת מגוריהם.

יחד הם החליטו על נוסח המודעה:

זוהר, זיו וקרן ,תלמידי כיתה ז', היו מעוניינים בעזרה במתמטיקה לאותו מספר שיעורים והתלבטו במי לבחור.

זוהר אמר שיבחר בנעם כי התשלום הראשון שלה הוא חינם.

זיו אמר שהוא יבחר בעמית, מפני שלה יש את הציון הגבוה ביותר במתמטיקה. לדבריו רועי לא הוגן בדרישותיו, כי למרות שהוא בעל הציון הנמוך ביותר, צריך לשלם לו את התשלום הראשון הגבוה ביותר. 

קרן טענה שככל שמספר השיעורים גדל כך גם הכדאיות משתנה. קרן החליטה להיעזר ברועי, מכיוון שהיא מעוניינת במחיר הנמוך ביותר לשיעור.  

מה דעתכם על טענותיהם של זוהר, עמית וקרן? 

במי הייתם בוחרים וכיצד הייתם מנמקים את בחירתכם?  

היעזרו ביישום הדינאמי הבא, בו מוצג גרף לכל הצעה.

- התאימו לכל הצעה את הגרף המתאים. בדקו האם צדקתם ע"י סימון התיבה.

- התאימו לכל ישר משוואה. בדקו האם צדקתם ע"י סימון התיבה.

- תוכלו לשנות את מספר השיעורים (בסרגל הגרירה) ולבדוק את התשלום לכל הצעה.

- שימו לב לטבלה הדינאמית משמאל.

א. אם זוהר זיו וקרן מתכננים ללמוד רק שלושה שיעורים פרטיים. מי מהם ישלם הכי מעט? הכי הרבה? 

כיצד ניתן לראות זאת בגרף ?

ב. אם היו מתכננים ללמוד שישה שיעורים, מה היתה הבחירה היקרה ביותר ? היקרה יותר ?

ולאחר עשרה שיעורים?

הסבירו כיצד מצאתם.

ג. לאחר כמה שיעורים שילמו קרן וזיו אותו מחיר? 

חברו משוואה המתארת מצב זה ופתרו אותה. כיצד בא לידי ביטוי פתרון זה בגרף?

ד. לאחר כמה שיעורים שילמו זוהר וזיו אותו מחיר? 

חברו משוואה המתארת מצב זה ופתרו אותה. כיצד בא לידי ביטוי פתרון זה בגרף ?

ה. לאחר כמה שיעורים שילמו זוהר וקרן אותו מחיר? 

חברו משוואה המתארת מצב זה ופתרו אותה. כיצד תוכלו להסביר פתרון זה בגרף ?

ו. לאחר כמה שיעורים יהיה לרועי, נעם ועמית מספיק כסף לצאת לטיול בשביל ישראל ?

חברו משוואה המתארת מצב זה ופתרו אותה. כיצד בא לידי ביטוי פתרון זה בגרף ?

האם שלושת החברים תרמו במידה שווה לקופת הטיולים המשותפת? האם הסדור ביניהם נראה לך הוגן?

הפעילויות עובדו על פי - שילוב החינוך לערכים בהוראת המתמטיקה, ד"ר יעל אדרי ("שער-חם", 2008)

מקורות נוספים: 

על מתמטיקה וערכים: 

מה למתמטיקה ולערכים?

האם יש סתירה בין חינוך לערכים לבין חינוך לחשיבה מתמטית? - מצגת מכנס למורים למתמטיקה בחינוך העל יסודי, 2008. (לתקציר)

פעילויות נוספות על חיתוך ישרים: 

חיבור לאינטרנט -  לראות מתמטיקה- פונקציות.

גניבת מכוניות -  לראות מתמטיקה- פונקציות.

תקציר|במבט אחר- לזכרו של מרטין גרדנר|פתרונות|بنظرة أخرى لذكرى مارتن جاردنر|حلول

מרטין גרדנר (1914-2010), גדול המשתעשעים במתמטיקה. 
כתב ספרים רבים ומדור פופולארי בעיתון סיינטיפיק אמריקן, על קסמים, חידות ומשחקים מתמטיים.
אמרו עליו שהוא גרם לאלפי ילדים להיות מתמטיקאים ולאלפי מתמטיקאים להיות ילדים.."ראו דף מחווה לזכרו באתר סיינטיפיק אמריקן, ודף מחווה נוסף לזכרו באתר Wolfram.

1. זריזות מחשבה

מלבן חסום ברבע מעגל כמתואר באיור. 

האם תוכלו לקבוע בזריזות מהו אורכו של האלכסון AC ?

שאלה ברוח דומה- בעיית השער הקטון בפיצוח "המחנה הכי הכי".

2. זה בתוך זה

אורך צלע הריבוע החיצוני 2. 

מהו שטחו של הריבוע הפנימי? 

פי כמה גדול שטח הריבוע הגדול משטח הריבוע הקטן?

3. תריסר גפרורים

אילו שטחים שלמים ניתן ליצור מתריסר גפרורים? 
לדוגמה, ריבוע בעל שטח של 9 יחידות רבועות, או צלב בעל שטח של 5 יחידות רבועות.

התוכלו לבנות מכל שנים עשר הגפרורים צורה בעל שטח של 8 יחידות רבועות? 6 ? 4?

 4. גמישושה - פלקסגון

בספרו הראשון בשנת 1956, פרסם מרטין גרדנר את הפלקסגון (Flexagon), ומאז הפך משחק זה לשגעון בקרב חובבי  שעשועי המתמטיקה. הפלקסגון, בתרגום חופשי מצולע גמיש, הוא מצולע המקופל מרצועת נייר ולו תכונה מדהימה שניתן לשנות את מספר הפנים שלו ואת צורתם כאשר מגמישים אותו. למשל, לגמישושה שנבנה יש שלושה צדדים... הכירו את הפלקסגון:

הוראות הכנה:

1. הדפיסו על נייר בריסטול את התבנית לגמישושה, וגזרו את הרצועה. 

2. חזקו את הקווים בעזרת עט וסרגל, כדי להקל על הקיפול בהמשך.

3. סמנו את צלעות המשולשים גם בצד השני של הרצועה. 

4. צבעו בשלושה צבעים או מספרו את המשולשים באופן הבא:

5. הפכו את הרצועה צבעו בשלושה צבעים או מספרו את המשולשים באופן הבא:

6. קפלו לפי האיור, משמאל הרצועה כלפי מעלה, ומימין לרצועה כלפי מטה.

7. כעת הפכו וקפלו לאורך הקו המסומן, כך שתקבלו משושה.

8. הכניסו את המשולש האחרון והדביקו אותו בזהירות.

9. אם קיפלתם נכון, תקבלו משושה עם שני צדדים בצבעים שונים (או ממוספרים 1 ו- 2).

10. קפלו וכופפו לאורך הקווים וגלו כיצד ניתן לגלות את המשושה בצבע השלישי (ממוספר 3). רמז- התבוננו באיור:

בואו נכין גמישושה מעוצב צבעו כל חלק באיור מטה באופן אחר.

כמה צדדים יהיו הפעם לגמישושה המעוצב?

ועוד. לכבוד מרטין גרדנר, סרטון להכנת פלקסגון בעל שישה צדדים שונים!

אם נדבקתם בשגעון הפלקסגון , תוכלו ללמוד עוד בפורטל הפלקסגון.

עוד חידות ומשחקים של מרטין גרדנר:

ט"ו בשלט- אלף אפס-  משחק אינטראקטיבי על פי מרטין גרדנר

קח אחד וקבל 21 - אלף אפס - חידה.

מזיזים את הזוזים, ד"ר זיווה דויטש, פרופ' בנימין וייס, פרופ' מיכה א. פרלס - מאמר המתאר משחק Bulgarian Solitaire מאת מרטין גרדנר.

אתגרים- מגזין חידות- שלש חידות מאת מרטין גרדנר, מתוך ספרו AHA.

אוסף חידות של מרטין גרדנר באתר PUZZLES.COM

Hexaflexagons, Probability Paradoxes, and the Tower of Hanoi- קישור לספרו הראשון של מרטין גרדנר של משחקים וחידות מתמטיות.

לכבוד יום ההולדת 90 למרטין גרדנר, על"ה  34, פרופ' נצה מובשוביץ הדר. במאמר מתואר פועלו ודוגמה לקסם מתמטי הנקרא "תעלול הפסנתר".

תקציר|ציור באדום כחול וצהוב |פתרונות|رسم بالأحمر بالأزرق و بالأصفر |حلول

מונדריאן (1872-1944), צייר הולנדי, חלוץ הסגנון האבסטרקטי. 

מונדריאן העריך מאד את יופייה של המתמטיקה ובמיוחד של הגיאומטריה ובטא זאת בציוריו. הוא שאף להגיע לפשטות, איזון והרמוניה באמצעות ציור של רשתות של קווים מקבילים ואנכיים,

שימוש בצבעי היסוד ושמירה על יחסים מתמטיים. האיזון מושג על ידי ניגודים ומובע באמצעות הקו הישר והזווית הישרה. בשנים 1921-1943 צייר סדרה של ציורים

הנקראת: קומפוזיציה בצהוב, כחול ואדום.

היו גם אתם מונדריאן ליום אחד...

1.  קחו דף ושרטטו ישרים בצבע שחור באופן הבא:

שרטטו ישר AB המאונך ל AC:

שרטטו ישר FE המאונך ל- AC: 

שרטטו ישר GH  המאונך ל- AB:

א. מה תוכלו לומר על הישרים FE ו-AB? הוכיחו.

ב. מה תוכלו לומר על הישרים FE ו-GH? הוכיחו.

ג. מה תוכלו לומר על המרובע EKGA? הוכיחו.

ד. נתון ABCD  מלבן. מה תוכלו לומר על המרובע DFKH? הוכיחו. 

ה. ידוע כי FD=DH. מה תוכלו לומר על המרובע DFKH? הוכיחו.

השלימו את היצירה- הוסיפו ישרים נוספים מאונכים ומקבילים לישרים הקיימים וצבעו באדום, כחול וצהוב את חלק מהמלבנים. השאירו חלק מהמלבנים צבועים בלבן.

תוכלו להתנסות ביצירות נוספות במשחק האינטרקטיבי. 

2. אילתורים

א. שרטטו מלבן שמידותיו הן: 6x7 סמ"ר. 

    מהו שטחו? שרטטו את הישר EF כך ש:

    ושרטטו את הישר GH כך ש: 

ב. צבעו את המרובעים הכחול והאדום, חשבו את מידת האורך והרוחב שלהם.

ג. ידוע שהמרובע הצהוב הוא מלבן ששטחו 1 סמ"ר. 

   חשבו מהו היחס בין השטחים הצבעוניים לשטח הלבן. 

   האם לדעתכם יחס זה מוסיף לאיזון וההרמוניה של הציור?

3. מונדריאן בתנועה

    באמצעות הציור הדינאמי  של מונדריאן בתנועה תוכלו ליצור יצירות דומות לזו של מונדריאן. 

    הזיזו את הישר המאונך GH (ע"י הזזת הנקודה G), כך ש- AG= 3 . 

    התבוננו בציור החדש, האם אהבתם אותו? האם לדעתכם הוא מאוזן והרמוני?

א. חשבו את מידות המלבנים הצבועים בציורכם החדש.

ב. חשבו את היחס בין השטחים הצבעוניים לשטח הלבן.

ג. שנו שוב את הציור באמצעות היישום מונדריאן בתנועה, הפעם כרצונכם.

    האם תוכלו למצוא ציור בו שטח המלבנים הצבעוניים שווה לשטח המלבנים הלבנים?

ד. בערוב ימיו, האמין מונדריאן שככל שהשטח הלבן גדול יותר הציור יותר מאוזן ומשרה שלווה.

    ציירו ציור כזה באמצעות  היישום מונדריאן בתנועה וחשבו את היחס בין השטחים

    הצבעוניים לשטח הלבן. 

    לדוגמה,  שנו את הציור כך שאחת מצלעות המלבן האדום והמלבן הכחול תהיינה 1 ס"מ.

4. הפסים השחורים בציור

מונדריאן נתן גם חשיבות לפסים השחורים בציוריו, המקיפים ותוחמים את המלבנים השונים.

חשבו בכל אחד מהציורים שלכם את ההיקף של שני המרובעים הכחול והאדום.

בדקו בציור הדינאמי, האם תקבלו תוצאה דומה עם שינוי מימדי המלבנים? הסבירו את התוצאה. 

התוכלו להסביר תופעה זו גם באופן אלגברי?

מקורות נוספים: 

The (Mathematical) Problem of Mondrian’s Paintings

תקציר| מה ערך המערך? | המערך למורה| גרסה להדפסה

האם קרה לכם, שאחרי שפתרתם בעיה או חידה והתבוננתם בה שוב, גיליתם עוד ועוד דרכים לפתור אותה, חלקן פשוטות בהרבה מזו הראשונה?

הפעילות שלפניכם, מתחילה כחידה שניתן לפתור בדרכים מגוונות. מגוון הפתרונות והשאלות שבהמשך מאפשרים להתבונן על פעולות מתמטיות מוכרות באור חדש.

הפעילות פשוטה אך היא עוסקת באחד מהרעיונות המרכזיים של המתמטיקה.

1. גלו את המספר שבמשבצת הריקה

לפניכם מערך משבצות צבעוני:

2. האם יש רמזים עודפים?

א. הניחו שלכל המשבצות הצבועות באותו מילוי יש אותו ערך. האם תוכלו לגלות את המספר החסר מבלי להשתמש בכל המספרים הרשומים בשולי המערך?     

ב. נסו לגלות את המספר החסר בכמה שיותר דרכים.

ג. אם כן – נסו להשאיר מספר מינימלי של מספרים שמאפשר לגלות את המספר החסר.

 

---

3. בדרך שלהם

אור אמרה: אני ראיתי שסכום המספרים בשתי השורות התחתונות הוא 22 והבנתי שסכום המספרים בעמודה הימנית הוא 11. למה אור מתכוונת, לדעתכם?

נועם אמר: אני הסתכלתי בשתי השורות האמצעיות והגעתי למסקנה שהערך של משבצת כחולה גדול ב- 3 מהערך של משבצת צהובה. אחר כך הסתכלתי בשתי העמודות הימניות והגעתי למסקנה שסכום המספרים בעמודה הימנית הוא 11. מה לדעתכם היו השיקולים של נועם?

אלון אמר: הדרך שלי דומה לשל נועם אבל אני קראתי לאדום A לכחול K ולצהוב Y. מהעמודות השמאליות למדתי ש- A=Y+1 . בשורה השנייה יש רק משבצות אדומות וצהובות ולכן יכולתי לכתוב 3Y+Y+1=5, וככה הגעתי לערכים של כל הצבעים. 

המשיכו את הדרך של אלון.

עינת אמרה: אני בכלל לא התייחסתי למילוי והגעתי לאותה תשובה. מה יכולה להיות הדרך של עינת? 

---

4. האם הרמזים מספיקים?

א. לפניכם חידת מספרים חדשה. 

ב. הפעם הרמזים מאפשרים למצוא רק חלק מהמספרים החסרים. 

ג. אם ניתן למצוא את הערך של שורה או עמודה – מצאו בדרכים שונות. 

ד. אם לדעתכם לא ניתן למצוא את ערכה של שורה או של עמודה – הסבירו מדוע לא ניתן לעשות זאת. 

  

 

---

5. הפינה לשיפוטיכם

 

לפניכם שתי הצעות למילוי מערך המספרים. (המספרים שהוספו בשולים רשומים באדום) 

כל אחד מהם בדק את החישובים של השני והם הגיעו למסקנה שאף אחד מהם לא טעה בחישוב. 

א. כיצד יתכן שכל אחד הגיע לתוצאות אחרות? 

ב. כיצד קרה שרוב המספרים בשוליים זהים בהצעות של שי ותמר?

 

 

---

6. הפינה לשיפוטיכם

 

א. ענו בלי לפתור משוואות
המחיר של 3 כרטיסי נוער ו- 2 כרטיסי מבוגר להופעה בפארק הוא 120 ₪.
המחיר של 6 כרטיסי נוער ו- 5 כרטיסי מבוגר לאותה הופעה הוא 270 ₪.
זוג הורים רוצה להגיע להופעה עם שני ילדיהם. כמה ישלמו?

 

ב. לכל אחת מן המשוואות הבאות קבעו את מספר הפתרונות.

 

 

 

 

---

 7. שומרי משקל

 

 

 

 

 

 

 

 

 

 

 

 

 

---

8. מפלצות ידידותיות – עם משוואות כאלה, מי צריך מחשבון?

א. פתרו ללא מחשבון את מערכת המשוואות

ב. נסו לחבר עוד מערכות משוואות ידידותיות עם חזות מפלצתית