זהו את הזהות הטריגונומטרית

תקציר| זהו את הזהות הטריגונומטרית| פתרונות| ميّزوا المتطابقات المثلثية| حلول

1. זהויות טריגונומטריות לסכום זוויות

באיור הבא נתון DB=1.

א. איזה קטע באיור שווה ל- (sin(α+β ?   

    איזה קטע באיור שווה ל- (cos(α+β ? 

ב. שנו באיור הדינאמי את הזווית α באמצעות הקודקוד A,     

    כך שסכום הזוויות α+β  נשאר קבוע.   

    אילו גדלים משתנים באיור ואילו נשמרים? 

    האם מתקיים sin(α+β)=sinα+sinβ ?

    האם מתקיים cos(α+β)=cosα+cosβ ?

ג. שנו באיור הדינאמי את הזווית β באמצעות הקודקוד B,   

    כך שסכום הזוויות α+β למעשה משתנה.

    אילו גדלים משתנים באיור ואילו נשמרים? 

    האם מתקיים sin(α+β)=sinα+sinβ ?

    האם מתקיים cos(α+β)=cosα+cosβ ?

*  אילו זוויות α, β מקיימות sin(α+β)=sinα+sinβ ?

   ברצוננו להביע את (sin(α+β באמצעות sinα ו- sinβ בלבד. 

ד. הביעו את אורכי הקטעים:

GH, BF, HF, DG, DH, BH באמצעות β,α בלבד.      

ה. רשמו נוסחאות מתאימות:

_________________ = (sin(α+β

_________________ = (cos(α+β

ו. רשמו נוסחאות מתאימות לזווית כפולה:

_________________ = (sin(2α

_________________ = (cos(2β

מקור: הוכחות ויזואליות: השקפותיהם ואמונותיהם של התלמידים, רז הראל טומי דרייפוס, על"ה 41

2. זהויות טריגונומטריות לזווית כפולה

א. הסבירו מדוע זווית AOB> כפולה מזווית BAM>  

ב. עקבו באיור הדינאמי אחר השתנות הזוויות וערכי הסינוס שלהן. 

ג. הביעו את AM בשתי דרכים:

    1) בעזרת משולש ΔAOM  

    2) בעזרת משולש ΔABM 

    מה ניתן להסיק?  

ג. כיצד תוכיחו את הנוסחה כאשר הזווית AOB> קהה?

ד. הביעו את OM בשתי דרכים. מה תוכלו להסיק הפעם? 

מקור: NRICH

3. עוד זהויות טריגונומטריות לזווית כפולה 

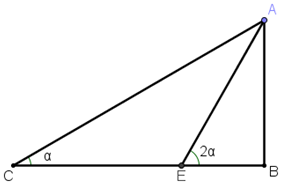
באיור הבא נתון CB=2.

נסמן t=tanα.

הביעו את אורכי צלעות המשולשים באיור באמצעות t.

הוכיחו באמצעות האיור את הזהויות הטריגונומטריות הבאות לזווית כפולה:

4. זהויות טריגונומטריות מפתיעות 

ידועה הנוסחה: 

נסמן tanα=t. הוכיחו את הזהויות ושימו לב לתופעה המפתיעה:

מה נקבל אם נרשום ממול כל אחד מהזהויות את המקדמים של t מהמונה ומהמכנה בסדר עולה?

מהי הנוסחה ל- (tan(5α?  ל- (tan(nα?

זהויות טריגונומטריות בשילוב גישת "מה אם לא?" - גילה רון, אורית זסלבסקי, קשר חם.

משחקים ודפי עבודה לתרגול בטריגונומטריה - NCTM