א. הגופים המשוכללים

תקציר | האם הכדורגל הוא עגול?|  בערבית

ראשית נכיר את חמשת הגופים המשוכללים, הידועים כגופים האפלטונים:

מתוך ויקיפדיה

מה מייחד את הגופים המשוכללים?

1. כל הפאות בגוף חופפות.
2. בכל קודקוד נפגשים אותו מספר של פאות.

צפו בסרטון חמשת הגופים המשוכללים מאת numberphile.
הכירו את הגופים ושאלו את עצמכם מדוע קיימים אך ורק חמישה גופים משוכללים?

בפעילות האינטראקטיבית הבאה תוכלו לצפות באנימציה תלת מרחבית של חמשת הגופים ולסובב אותם בעצמכם. ניתן גם לסמן את הפאות ולספור אותן (F-faces), את הקודקודים (V-vertices) ואת המקצועות (E-Edges).
באפשרותכם גם להדפיס את הפריסות ולבנות את הגופים.

השלימו את הטבלה האינטראקטיבית ובדקו תשובותכם.

מצאו קשרים אפשריים בין מספר הפאות (F) , מספר הקודקודים (V) ומספר המקצועות (E).

מקורות נוספים:
בנה בעצמך גופים משוכללים (בעזרת קיפול וללא דבק), שמואל אביטל, קשר חם.
למה קיימים רק 5 פאונים משוכללים? כיתהפיתה
אוילר וגאוס ביצירתם ובחייהם - אלה שמוקלר, קשר ח"ם

 המשך לחלק ב' - מהם גופים חצי משוכללים? ואיזה גוף הוא הכדורגל?

בדרך לפיתגורס- ריבועים רוקדים

תקציר| בדרך לפיתגורס| פתרונות| الطريق الى فيتاغوروس| حلول

א. המשחק "השלימו לריבוע"

בואו נשחק משחק. ברשותכם רשת נקודות. 
כל שחקן בתורו בוחר נקודה על הרשת ומסמנה בצבע משלו. 
השחקן המנצח יהיה הראשון אשר יהיו לו ארבע נקודות שניתן לחברן לריבוע. 
ריבוע יכול להיות מסובב ומכל גודל.

ניתן לשחק במשחק האינטראקטיבי מול המחשב או מול חבר, או בעפרון ונייר על דף הרשת הבא.

ב. לפניכם כמה ריבועים מתוך המשחק. 
המרחק בין כל שתי נקודות יחידה.

התוכלו לחשב את אורך הצלע של כל ריבוע ?שטחו של כל ריבוע?

ודאי שמתם לב שיש ריבועים שמיד ניתן לראות את אורך הצלע שלהם ומכאן בקלות לחשב את שטחם.  כיצד תאפיינו ריבועים אלו ואת הקשר בין אורך צלע הריבוע ושטחו?

אך, לא קל למצוא באופן מיידי את אורך הצלע של הריבועים "המסובבים". האם מצאתם? הכיצד?
הנחיה- מצאו את השטח של  הריבוע המסובב בעזרת ריבוע נוסף החוסם אותו וארבעת המשולשים המקיפים אותו.

ג. בחקירה הבאה תוכלו להיעזר ביישום דינאמי בו ניתן לסובב ריבוע בעזרת החיצים.

(1). נתבונן בסדרת ריבועים מסובבים שהוטו יחידה אחת מעלה.

חשבו את שטחי הריבועים בסדרה. האם מצאתם חוקיות בין שטחי הריבועים הללו?
התוכלו לדעת מה יהיה שטח הריבוע הבא בסדרה?

(2). בדקו האם קיימת חוקיות לשטח של סדרת ריבועים שהוטו 2 יחידות מעלה. 
      3 יחידות ? 4 יחידות? n יחידות?

                                                  ריבוע הנטוי 4 יחידות          ריבוע הנטוי 3 יחידות             ריבוע הנטוי 2 יחידות

הפעילות פותחה לפי nrich (ניתן לצפות גם בסרטונים להדגמת השיעור)

מקורות נוספים להעמקה והרחבה:

• מאדריכלות נוף למשפט פיתגורס- הצעות לפעילות של מטח
• Pythagorean Theorem- IES - אוסף יישומים דינאמיים של הוכחות למשפט פיתגורס ושימושים בבעיות שונות. 
• כתבה וערכה - נאווה מזרחי חט"ב "מיכה רייסר"- ראשון לציון
•  הרפתקה פיתגוראית- מאמר מבית "אלף אפס" המספר את סיפור מסע היתדות בן ה-3700 שנים על שלשת המספרים הידועה כשלשת פיתגורס. כתבו: זיוה דויטש, עקיבא קדרי
•  משפט פיתגורס- מבחר הוכחות ללא מילים, מאמר של "אלף אפס" ועוד חידות בנושא ויישומו.
•  "כל דבר הוא מספר"- מאמר מאת "בארץ הדעת", על תפיסותיו של פיתגורס את מושג המספר ואת המספרים הרציונאליים. כתב: רועי יהושע.
• מצגת על הוכחות של משפט פיתגורס, שלשות פיתגוריות ועוד - פסגה הרצליה, מרים עוזר, רונית רביע, ריטה שכטר
• נגריה מתמטית - בעיית החדש, קשר חם - מוצגת בעיה העוסקת בבניית ריבוע ששטחו שווה לשטח מלבן נתון. הבניהמתבססת על משפט פיתגורס, ומובילה להוכחתו בדרך גיאומטרית. מצורף פתרון לבעיה.

עוד פיצוחים:

• אוצרות פיתגורס - בפעילות חידות לחישוב שטחים הדורשות יישום של משפט פיתגורס וידע על המעגל.
• משימה פרחונית - במשימה מוצגות צורות גאומטריות בעיצוב של פרחים ויש לחשב את שטחן.
• ללכת על פני הקוביה והתיבה - יישום משפט פיתגורס במרחב
• אנשי החידות מהודו - בפעילות כמה בעיות עתיקות מהודו העוסקות במשפט פיתגורס.

playing math with your food By George Hart  for the museam of mathematics 

ב. מהם גופים חצי משוכללים? ואיזה גוף הוא הכדורגל?

תקציר |  האם הכדורגל הוא עגול? |  בערבית

תרגיל בדמיון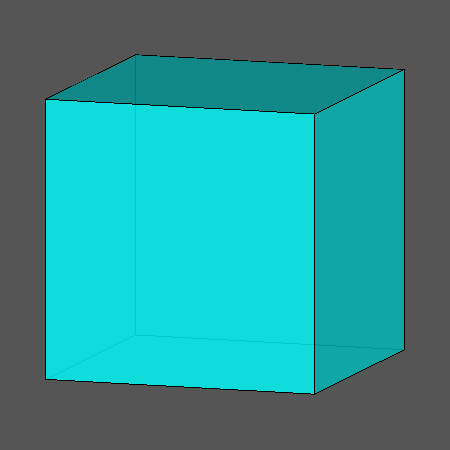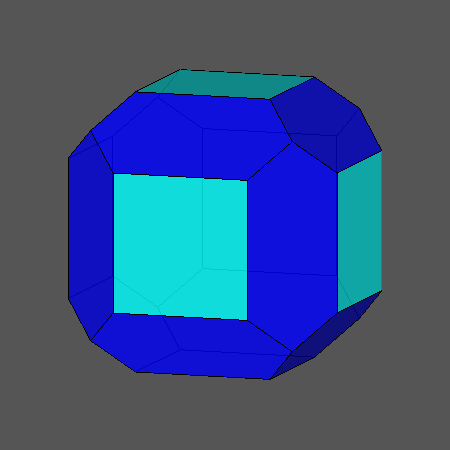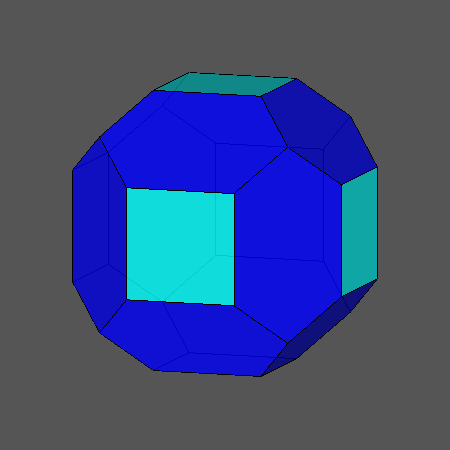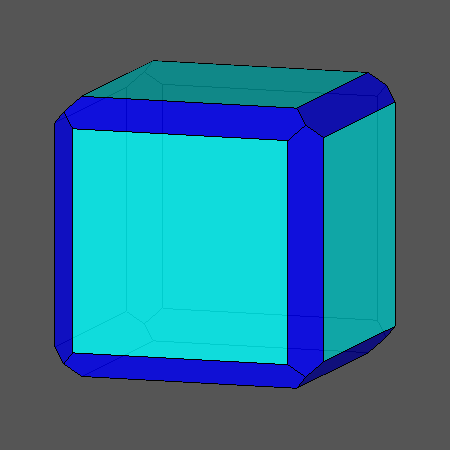 

בפניכם קובייה. כעת נסו לדמיין שקוטמים כל פינה בקובייה, איזה גוף נקבל? אילו מצולעים תקבלו בכל פינה?
כמה מצולעים כאלה יהיו בגוף החדש? האם בגוף הקטום יהיו גם מצולעים אחרים כמה? ראו אנימציה.

ראו גם פיצוח "לחתוך את הקוביה" בו תוכלו להתנסות בעזרת יישומון בחיתוך הקובייה.
גוף חצי משוכלל הוא גוף שכל פאותיו מצולעים משוכללים (מסוגים שונים), ומכל אחד מקדקודיו יוצא אותו מספר מקצועות (צלעות).

ארכימדס חקר את הגופים הקטומים של הגופים המשוכללים, וקיבל אוסף חדש של 12 גופים חצי משוכללים, הידועים בשם פאונים ארכימדים. המפורסם שבהם הוא העשרימון הקטום, הוא הכדורגל. קראו מאמר באלף אפס בנושא, אל תקלקל לי את המעגל, מאת זיוה דויטש ועקיבא קדרי.

ראו סרטון מאת NuberPhile על העשרימון הקטום, הוא הוא הכדורגל! שימו לב כמה פיאות לכדורגל ומהן תכונותיהן?

בנו לעצמכם כדורגל מנייר.

מקורות נוספים:

הסברים ואנימציות על גופים חצי משוכללים (באנגלית)

 המשך לחלק ג' - האם גם אויילר שיחק בכדורגל?

ג. האם גם אויילר שיחק בכדורגל?

תקציר |  האם הכדורגל הוא עגול?  |  בערבית

אוילר, מתמטיקאי ידוע מהמאה ה-18, חקר את הפאונים ותכונותיהם, בבעיות שעסקו בהן כבר היוונים הקדמונים, וגילה תובנה שחמקה מעיני המתמטיקה במשך אלפיים שנים לערך, נוסחת אוילר. הוא גילה קשר מספרי בין מספר מספר הפאות (F), מספר הקודקודים (V) ומספר המקצועות (E).

אולי כבר גיליתם בעצמכם?       

קראו עוד על הגופים האפלטוניים, נוסחת אוילר לפאונים, וכדורגל בבלוג "לא מדויק".

נשאלת השאלה האם הכדורגל וגופים אחרים גם הם מקיימים את נוסחת אוילר? בדקו בעצמכם את הנוסחה עבור הכדורגל, העשרימון הקטום, וצפו בסרטון.

קראו עוד על נוסחת אויילר (באנגלית).

מקורות נוספים:
אוילר וגאוס ביצירתם ובחייהם - אלה שמוקלר, קשר ח"ם
הגופים האפלטוניים, נוסחת אוילר לפאונים, וכדורגל - רשומה מאת גדי אלכסנדרוביץ' בבלוג "לא מדויק"

 המשך לחלק ד' - כדורגל בחלל

ד. כדורגל בחלל

תקציר |  האם הכדורגל הוא עגול? |  ערבית

רגע של היסטוריה... ממש קרובה.

בשנת 1996 הוענק פרס נובל לכימיה לשלושה כימאים: קרוטו, קארל, וסמאלי על גילויים של הפולרנים, מולקולות של פחמן טהור שחלקם מסודרים ככדורים, "כדורי באקי". 

הייחוד של התגלית היה לא רק בהדגמת קיומו של הפולרן, אלא גם בכך שהסתבר שאטומי הפחמן נוטים להסתדר באופן טבעי במבנה זה. 

טלסקופ החלל שפיצר של נאס"א גילה לראשונה בחלל חלקיקים בצורה של כדורגל (buckyball) הנקראים פולרון, פחמן 60. הצורה שיוצרים 60 אטומי פחמן ב-C60, היא פאון ארכימדס הקרוי "איקוסהדרון קטום", הבנוי ממחומשים ומשושים בדומה לכדורגל. האסטרונומים גילו כדורים זעירים אלו סביב כוכב חם קטן הרחוק 6500 שנות אור מכדור הארץ, בכמות היכולה ליצור 10,000 הרי אוורסט...

שימושי כדורי הפחמן 60 

פחמן ב-C60, היא פאון ארכימדס הקרוי "איקוסהדרון קטום", הבנוי ממחומשים ומשושים בדומה לכדורגל. האסטרונומים גילו כדורים זעירים אלו סביב כוכב חם קטן הרחוק 6500 שנות אור מכדור הארץ, בכמות היכולה ליצור 10,000 הרי אוורסט...

כדורי הפולרנים ידועים בתכונות החוזק שלהם (חזקים יותר מיהלום), בגמישות, עמידות לחום ומוליכות גבוהה. במהלך העשור האחרון, התכונות הפיזיקאליות והכימיות של פולרנים, היו נושא חם בשדה המחקר והפיתוח. נמצאו שימושים רבים לפחמן 60 בתחום הרפואה, הננוטכנולוגיה ועוד. הפחמן 60 מהווה בסיס ליצירת חומרים קלים וחזקים - דבר השימושי בשביל בנייה של שכפ"צים, אופניים ומטוסים - ואף מדברים על בנייה של 'מעלית לחלל החיצון' המבוססת על ננו צינורות.

לכתבה: Tiny 'Soccer Ball' Space Molecules Could Equal 10,000 Mount Everests

לסרטון: 

מקורות נוספים:
אנימציות של גופים
הכדור הוא עגול (כלומר, בערך) – מחווה מולקולרית למונדיאל, הידען

 המשך לחלק ה' - הכדורגל במונדיאל

תקציר|לחתוך את הקובייה|قص المكعب

1. המתנה 

על פני קופסת מתנה בצורת קוביה שאורך מקצועה 10 ס"מ, 

הודבקו שני סרטים לקישוט כמתואר בציור.

א. מהו אורך הסרטים?

ב. התוכלו לדעת מהי הזווית בין הסרטים?

רמז - השלימו למשולש ואפיינו אותו.

מקור - Puzzle Playground

 2. קוביית חימר

מהפינה של קוביית חימר (או פלסטלינה) שאורך מקצועה 10 ס"מ, נחתך חתך מישורי בצורת משולש שווה צלעות. (ראו איור)

א. ידוע שאחת מנקודות החיתוך היא אמצע המקצוע של הקובייה. הסבירו היכן יש למקם את שתי נקודות החיתוך הנוספות בכדי ליצור חתך מישורי של משולש שווה צלעות. 

חשבו את אורך צלע המשולש ואת שטחו. 

ב. קוביית חימר נוספת, שאורך מקצועה 10 ס"מ, נחתכה בפינתה בחתך מישורי של משולש שווה צלעות שאורך צלעו 1 ס"מ. הסבירו היכן יש למקם את נקודות החיתוך על מקצועות הקובייה. מה שטחו של

המשולש?

ג. היכן יש למקם את נקודות החיתוך על מקצועות הקובייה כך שיתקבל חתך מישורי של משולש שווה צלעות בעל השטח הכי גדול ? חשבו את אורך צלעו ואת שטחו. 

צפו בסרטו או העזרו ביישום הדינאמי, גאוגברה.

ד. הפעם חתכו מכל אחת מפינות קוביית החימר, מאמצע כל מקצוע, חתך מישורי של משולש שווה צלעות. (חזרו על הפעולה מסעיף א' לכל קודקוד של הקובייה).

תארו את הגוף שנותר . (ניתן להיעזר ביישומון)

שאלת אתגר- תארו איזה גוף יתקבל אם נחתוך מכל אחת מפינות קוביית החימר , חתך מישורי של משולש שווה צלעות ולאו דווקא מאמצע כל מקצוע.

3. חתכי הקובייה

צרו קובייה מחימר או פלסטלינה. בעזרת חוט ניילון חתכו את הקובייה לשניים. 

אלו  צורות של חתכי מישור תוכלו לקבל? 

קל מאוד לחתוך קובייה במישור ולקבל חתך של משולש שווה צלעות. צריך פשוט לחתוך פינה אחת של הקובייה ולהקפיד שמידות האורך של החתך יהיו שוות.

עוד יותר פשוט לחתוך קובייה במישור ולקבל חתך שצורתו ריבוע. כיצד?

צרו חתכים מישוריים של קובייה בעזרת חיתוך קוביית חימר או בעזרת היישום הדינאמי.

האם תוכלו ליצור את הצורות הבאות? אם כן, הסבירו כיצד. אם לא, מדוע?

א. ריבוע

ב. משולש שווה צלעות

ג. משולש שאינו שווה צלעות

ד. מלבן שאינו ריבוע

ה. מחומש משוכלל

ו. מחומש שאינו משוכלל

ז. משושה

ח. מתומן

ט. מקבילית שאינה מלבן

י. מעגל

טיפים נוספים: ניתן ליצור חתכים מישוריים של קוביה גם בעזרת יישום נוסף. (נדרש ג'אווה)

אפשרות נוספת להמחיש את חתכי הקובייה היא ע"י מילוי חלקי של קובייה שקופה בנוזל צבעוני, (מיץ פטל, למשל) והטייתה של הקוביה.

נערך על פי Learning Math - Solids, Cross Section

מקורות נוספים:

חתך קובייה- גליונות לחשבון 54, שמואל אביטל.

חתכי קובייה - גליונות לחשבון 14, שמואל אביטל.

הרחבה למתעניינים (אנגלית).

Wismaat- Gometry 3D - סביבה ממוחשבת לגופים במרחב כולל חתכים ופריסות של מכון המחקר ההולנדי Freudenthal. (מומלץ!)

חישובים במרחב

תקציר|חישובים במרחב| פתרונות|حسابات في المساحة 

1. המתנה 
אריזת מתנה בצורת תיבה נעטפה בנייר אריזה, כך ששטח הפאות של התיבה הוא: 3  סמ"ר, 12 סמ"ר ו-25 ס"מר.

התוכלו לחשב את מימדי התיבה? (אורך,רוחב וגובה)

אם נתון ששטח הפאות הוא a,b,c  סמ"ר.

הביעו את מימדי התיבה באמצעות a,b,c.

2. הכדור המתגלגל

כדור טניס בקוטר 10 ס"מ נארז בקובייה התגלגל לפינה.

התוכלו לדעת מה המרחק של מרכז הכדור מפינת הקוביה?

3. הנמלה העמלה  

נמלה עמלנית יצאה לטייל על פני חרוט, שמידותיו מתוארות בציור,  במטרה להגיע מנקודה A לנקודה B.

התוכלו לומר לנמלה מהו המסלול הקצר ביותר?

4. הקובייה שבפנים

בתוך קובייה שנפחה 10 ס"מק , חסום כדור שבתוכו חסומה קובייה קטנה יותר.

התוכלו לחשב את נפח הקובייה החסומה בפנים?

שטחים בריבוע

תקציר|שטחים בריבוע

1. ריבוע סוב סוב 

הריבוע האדום מסתובב סביב מרכז הריבוע הכחול, כך שאחד מקודקודי הריבוע האדום מונח במרכזו של הריבוע הכחול. ראו את היישום הדינאמי  .

א. אם שני הריבועים שווים בגודלם, הראו כי בכל כוון שהוא הריבוע האדום מכסה רבע משטחו של הריבוע הכחול.

ב. אם נגדיל את הריבוע האדום, האם עדיין השטח שהוא יכסה יהיה רבע משטח הריבוע הכחול? נמקו.

ג. אם נקטין הריבוע האדום, האם עדיין השטח שהוא יכסה יהיה רבע משטח הריבוע הכחול?
אם כן, באיזה מקרה? אם לא, מדוע?

2. טנגרם

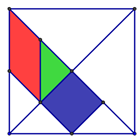במשחק טנגרם המפורסם מחולק הריבוע, 
שאורך צלעו 12 ס"מ, לשבעה חלקים.חשבו את השטחים הצבועים של: 
  א.      הריבוע 
  ב.      המשולש הקטן 
  ג.       המקבילית

שחקו במשחק הטנגרם האינטראקטיבי.

ועוד ברקנים מאלף אפס -  איזה שטח גדול יותר, האדום או הכחול?

3. ריבוע בריבוע  

א. על  כל אחת מצלעות ריבוע שאורך צלעו יחידה, הקצו נקודת אמצע, ויצרו ריבוע פנימי. (ראו איור)
הסבירו מדוע המרובע הפנימי הוא ריבוע.
מצאו את שטחו.
(רמז- נסו לבנות פאזל)

ב. שנו את האיור ביישום הדינאמי  כך שהקצו על כל 
צלע הריבוע נקודה ביחס 1:3.
האם המרובע הפנימי הוא ריבוע?
מצאו את שטחו.

ג. שנו את האיור ביישום הדינאמי  כך שהקצו על כל צלע   
      נקודה ביחס 
      האם המרובע הפנימי הוא ריבוע?
      מצאו את שטחו.

4. שטחים בריבוע

בריבוע, שאורך צלעו יחידה, הקצו אמצע קטע על אחת הצלעות ויצרו שטחים כמתואר באיור.

מצאו מהו יחס השטחים שנוצרו באיור א?

כיצד ניתן להיעזר באיור ב לחישוב השטחים? הסבירו את הבנייה.

תקציר| הנקודה שבפנים| نقطة في الداخل

1. חלוקת שטחים 

במגרש כדורגל הציב השופט את הכדור בנקודה P בתוך הריבוע וחילק את שטח המגרש לשתי הקבוצות באופן הבא:

קבוצה א תקבל את השטח הכתום S1+S3.

קבוצה ב תקבל את השטח הסגול S2+S3.

תוכלו להיעזר ביישום הדינאמי  לשם החישובים עבור נקודות P שונות.

א. היכן לדעתכם יש למקם את הנקודה P כך שהחלוקה תהיה הוגנת? מדוע?

ב. כיצד תשתנה החלוקה (אם בכלל) אם המגרש יהיה מלבני? נמקו.

שוב תוכלו להיעזר ביישום הדינאמי  לשם שינוי מימדי המלבן.

ג. כיצד תשתנה  החלוקה (אם בכלל) אם הנקודה תהיה מחוץ למגרש? נמקו.

 2. חלוקת נפחים

נתונה תיבה מלבנית ובתוכה נלכד עכביש בנקודה P שהיא מרכז התיבה. העכביש מתח חוטים לפינות התיבה כך שיצר פירמידות אשר קודקוד הראש שלהן הנקודה P ובסיסן פאות

התיבה.

א. כמה פירמידות נוצרו באופן זה?

ב. מה תוכלו לומר על סכום הנפחים של שתי פירמידות נגדיות (שבסיסן מונח על פיאות נגדיות).

ג. כיצד ישתנו הנפחים אם הנקודה P תנוע למקום אחר במרחב התיבה? נמקו.הנחיה – ניתן להיעזר בפתרון השאלה הקודמת.

3. המרחק הנעלם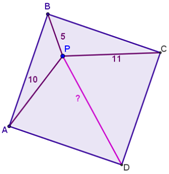  

במגרש כדורגל ריבועי נמצא השחקן בנקודה P.

ידוע לו כי מרחקו מפינת המגרש בקודקוד A הוא 10מטרים, מהקודקוד B הוא 5 מטרים ומהקודקוד C הוא 11 מטרים. בשאלות הבאות תוכלו להיעזר ביישום הדינאמי  .

א. התוכלו לעזור לו ולקבוע מהו מרחקו מפינת המגרש בקודקוד D?

ב. כיצד ישתנה המרחק PD כאשר המגרש יהיה מלבני?

ג.  מה יהיה המרחק PD אם השחקן יהיה מחוץ למגרש?

ד.  מה יהיה המרחק PD אם נתון כי: PB=a ,PA=c ,PC=b?

4. תיבה

נתונה תיבה ובתוכה נלכד עכביש בנקודה P. העכביש מתח חוטים לפינות התיבה כך ש:

תקציר|מן הפנים אל החוץ 

2. מן הפנים אל החוץ

א. נתונות שלוש נקודות A, B, C שהן אמצעי הצלעות של משולש כלשהו, אך המשולש המקורי עצמו 
(DEFD) נעלם. בדקו ביישום הדינאמי  האם וכיצד ניתן ליצור את משולש DEFD:

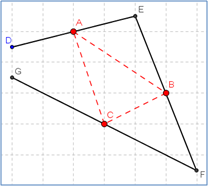- האם תמיד ניתן לבנות את המשולש על פי אמצעי צלעותיו?
- כיצד ניתן לבנות את המשולש המקורי? תארו את הבנייה ונמקו.
- האם קיים רק משולש אחד כזה?
- בהינתן שיעורי נקודות האמצע, התוכלו למצוא את שיעורי קודקודי המשולש המקורי.

ב. נתונות ארבע נקודות A, B, C, D שהן אמצעי הצלעות של מרובע כלשהו, אך המרובע המקורי עצמו 
(EFGH) נעלם. בדקו ביישום הדינאמי  האם וכיצד ניתן ליצור את המרובע EFGH:

- האם תמיד ניתן לבנות את המרובע על פי אמצעי צלעותיו? אם כן, באיזה תנאי?
- כיצד ניתן לבנות את המרובע המקורי? תארו את הבנייה ונמקו.
- האם קיים רק מרובע אחד כזה?

ג. האם וכיצד ניתן לבנות מחומש מחמש הנקודות של אמצעי הצלעות?

האם וכיצד ניתן לבנות משושה משש הנקודות של אמצעי הצלעות?

על כנפי הדמיון