תקציר|מערכת משוואות בשני נעלמים |פתרונות|معادلتان بمجهولين |

1. משוואות הקסם

1. בשיעורי הבית דנה התבקשה לפתור שלש מערכות של משוואות בשני נעלמים:

    דנה פתרה שתי מערכות משוואות ומצאה שפתרונן זהה והוא (x,y)=(−1,2).

    היא טענה שגם למערכת המשוואות השלישית אותו פתרון.

    האומנם? בדקו את פתרונה של דנה.

2. דנה טענה שיש למערכות המשוואות הללו מבנה מיוחד. התוכלו גם אתם לזהותו?

    תנו דוגמה למערכת משוואות דומה. מהו פתרונה?

3. דן ורונה בנו גם הם מערכת משוואות:

   פתרו את המשוואות. מה קיבלתם?

   מה מיוחד הפעם במבנה המשוואות?

4. עדי "הציצה" במחברות של דן ורונה ורשמה מערכת חדשה:

    האם 'הקסם' יעבוד גם במערכת של עדי ?

5. השלימו את המערכות הבאות כך יתקבל פתרון (x,y)=(−1,2):

6. שרטטו, במערכת צירים אחת, את ארבעת הישרים שמופיעים במערכות (1) ו-(2). בחרו מערכת משוואות 

    נוספת מבין המערכות (4) - (9) והוסיפו לשרטוט את שני הישרים הנוספים. מהי המשמעות הגיאומטרית 

    של כל הישרים הללו? 

7. מצאו תבנית כללית לרשום מערכות הקסם.     

    אתגר אלגברי -הוכיחו כי פתרון מערכת משוואות הקסם הוא (x,y)=(−1,2).

מעובד לפי "מתמטיקה בהנאה" של פרופ' אביטל.

סולמות טמפרטורה

במרבית ארצות העולם משתמשים באופן יומיומי בסולם הטמפרטורה של צלסיוס. במדינות ספורות, ביניהן ארצות הברית,משתמשים בסולם הטמפרטורה של פרנהייט. צלסיוס הגדיר את אפס מעלות כנקודת הקיפאון של המים וכ- 100 את  נקודת

הרתיחה של המים. ואילו פרנהייט הגדיר את נקודת האפס כטמפרטורה שאליה יורד קרח כתוש כאשר מערבביםאותו במלח וכ- 100 בטמפרטורה הממוצעת של חום האדם.

תיירים המבקרים בארצות בהן סולם טמפרטורה שונה מאשר בארצם , צריכים להמיר את הטמפרטורות של מזג האוויר למשל, לסולם המוכר להם. בתמונה מוצג מדחום המכויל לפי שתי השיטות ,של צלזיוס ושלפרנהייט .המדחום מאפשר המרת טמפרטורות שבין 25° ל 50° צלזיוס בלבד. הוא איננו מאפשר המרת טמפרטורות גבוהות יותר.דרך שיטתית יותר להמרת הטמפרטורה מסולם פרנהייט לסולם צלזיוס ניתנת באמצעות הנוסחה: 

(מסמנים טמפרטורה הנמדדת בסולם צלזיוס ב-C ובפרנהייט ב-Fׂ)

שאלה 1

א. איזו טמפרטורה במעלות צלזיוס מתאימה ל - 86° פרנהייט?

   בדקו האם התוצאה מתאימה לתמונה.

ב. איזו טמפרטורה במעלות פרנהייט מתאימה ל - 40° צלזיוס?

   בדקו האם התוצאה מתאימה לתמונה.

שאלה 2

לפי סולם צלזיוס , מים קופאים ב - 0° ורותחים ב- 100° בתנאי שהלחץ החיצוני הפועל עליהם הוא אטמוספרה אחת. לפי סולם פרנהייט מים קופאים ב - 32° ורותחים ב - 212°. 

א. מהו הפרש הטמפרטורה מנקודת הקיפאון לנקודת הרתיחה בסולם פרנהייט?

ב. מהו הפרש הטמפרטורה מנקודת הקיפאון לנקודה הרתיחה בסולם צלזיוס?

ג. חשבו את היחס בין שני ההפרשים שקיבלתם

   רשמו אותו כשבר פשוט, מצומצם ככל האפשר.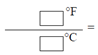

ד. מהו השינוי בטמפרטורה בסולם פרנהייט המתאים לשינוי של מעלה אחת בסולם צלזיוס?

שאלה 3

מצאו נוסחה המאפשרת המרת טמפרטורה מסולם צלזיוס לסולם פרנהייט.

שאלה 4

האם קיימת מידת חום בה הטמפרטורה שווה לפי שני סולמות המדידה?

אם כן – מהי ?אם לא – נמקו.

הפעילות לקוחה מתוך "אוריינות מתמטית" של האגף לתכנון ולפיתוח תכניות לימודים.

תקציר

שתי מכוניות יצאו למסלול נסיעה באותו כיוון. נקודת ההתחלה של המכונית האדומה היא 30 ק"מ אחרי נקודת ההתחלה של המכונית הכחולה.
שתי המכוניות יוצאות למסלול באותו זמן. 
מהירות המכונית הכחולה 50 קמ"ש ומהירות האדומה 35 קמ"ש.

הכניסו את הנתונים המתאימים לסימולציה וצפו בתנועת המכוניות ע"י לחיצה על Start.
תוכלו לעצור את המכוניות בכל רגע ע"י לחיצה על Stop.
תוכלו להסיע ידנית את המכוניות בעזרת Manual Animation.

א. מהי משוואת הישר המתארת את הדרך של המכונית האדומה? של המכונית הכחולה?

ב. מתי והיכן תשיג המכונית הכחולה את האדומה?

ג. מה יהיה המרחק בין המכוניות לאחר 4 שעות?

ד. מצאו בעזרת הסימולציה:

    1. מתי יפגשו המכוניות אם המרחק ההתחלתי בין המכוניות יהיה 60 ק"מ?

    2. באיזו מהירות צריכה לנסוע המכונית האדומה בכדי שיפגשו לאחר 3 שעות? לאחר 5 שעות?

    3. באיזו מהירות צריכה לנסוע המכונית האדומה בכדי שהיא לא תיפגש כלל עם המכונית הכחולה?

בעיות תנועה דינאמיות מהספר האלקטרוני "לראות מתמטיקה- פונקציות":

• נסיעות- באמצעות הכלי נסיעות על כביש חיפה - תל-אביב אפשר לתאר נסיעות של כלי-רכב בין כמה ערים הנמצאות לאורך כביש זה.
• טיולים שונים- בפעילות יש להתאים את הגרף לסיפור הטיול המתאים.
• גרפים לתיאור תנועה - בפעילות יש להתאים לסימולציה של תנועת המכוניות את הגרף המתאים.
• משאיות - קריאת גרף וחיבור גרפים לסיפור.
• תופסת - עקבו אחר הסימולציה למשחק תופסת ובעזרת הזזות תוכלו לשנות את הפונקציות המתארות את הריצה במשחקי תופסת אחרים.
• טיול אופניים -  תיאור בעיות תנועה באמצעות גרפים והזזותיהם.
• קטנוע ואוטובוסים - בניית פונקציות וגרפים לסיפורים באמצעות כלי ההזזות.
• תוכניות לטיול - בניית פונקציות וגרפים לסיפורים באמצעות כלי ההזזות.
• נסיעות ברכב - במשימה יש להתאים ביטויים של נסיעת הרכב לחלקים שונים של הזמן.
• טיולים ושיקופים - שלושה סיפורים אחרים שאפשר לתארם בגרף על ידי הפעלת שיקופים על חלקים של הגרף הנתון, בציר אופקי ובציר אנכי.
• תיאורים שונים של טיול -  משימה עוסקת בהרכבת ביטויים המתארים את הסיפורים של מטיילים שונים. ובמציאת ביטויים שקולים לאותו סיפור.
• מהירות מופרזת - מציאת ביטויים שקולים לפונקציות המתארות תנועה.

תקציר|בעיות תנועה בדרך אחרת |פתרונות

1. אופניים וקטנוע יצאו מתל אביב באותה שעה. רוכב האופניים נסע במהירות של 20 קמ"ש ורוכב הקטנוע במהירות של 32 קמ"ש. כעבור שעה וחצי יצאה מאותו מקום באותו הכיוון מונית שעקפה את האופניים ולאחר חצי שעה השיגה גם את הקטנוע. באיזו מהירות נסעה המונית?

א. מה מתארים הישרים OB, OC ו- AC?
    מה מתארות הנקודות A, B, C ?

ב. מהי משוואת הישר המתארת את תנועת רוכב האופניים? מה מציין שיפוע הישר?

ג. מהי משוואת הישר המתארת את תנועת רוכב הקטנוע? מה מציין שיפוע הישר?

ד. נסמן את זמן המפגש של רוכב האופניים והמונית ב- t.
    מהם שיעורי הנקודות A, B, C, D, E ,F.

ה. הביעו את מהירות המונית כפונקציה של t .

ו. הביעו את מרחק הנסיעה של המונית עד לנקודת המפגש עם הקטנוע בשני אופנים:

    1. לפי נוסחת המרחק (מכפלת הזמן במהירות).

    2. כסכום של שני מרחקים CE=CF+FE. (הסבירו)
        השוו בין שני הביטויים ומצאו את t.

דרך פתרון נוספת באמצעות השוואת ביטויים למהירות המונית בקטעי זמן שונים.

או באמצעות דמיון המשולשים   (ראו הדרכה לבעיה 3)

---

2.  דני ודינה יצאו להליכה באותו זמן, זה לקראת זו .

דני יצא מביתו במעלה אביב ודינה יצאה מביתה שבמעלה הסתוונית. הם חלפו זה על פני זו  והמשיכו בדרכם עד ליעדם, (דני למעלה סתוונית ודינה למעלה אביב) ומיד החלו לחזור אל הישוב ממנו באו. עד פגישתם השנייה (כשהלכו בחזרה) דינה עברה  שישה

קילומטרים יותר מדני.  דינה הגיעה בחזרה לביתה שעה אחרי פגישתם השנייה ואילו דני הגיע לביתו שעתיים וחצי אחרי פגישה זו.

מצאו את המהירויות של דני ודינה ואת המרחק בין הישובים.

 

במערכת הצירים הבאה מתוארים שני המסלולים של דני ודינה:

א. התאימו את הגרפים המתאימים לדרכם של דינה ודני ? מי הולך מהר יותר ?

ב. תארו במילים מה מתארות כל הנקודות המסומנות בגרף. (פרט ל-H ו-F).

ג. תארו במילים מה מתארים אורכי הקטעים AB, CF ו- HC .

ד. נסמן את אורך הקטע CF ב-d . הביעו באמצעות d את אורכי הקטעים HC ו- AB .

ה. תארו במילים מה מתארים הקטעים FD ו- HG . מהם אורכם ? 

ו. הביעו את המהירויות של דינה ושל דני באמצעות d.

ז. הביעו את הדרך שעבר כל אחד מהם עד לפגישה השנייה.

ח. השוו בין זמני ההליכה של דני ודינה עד לפגישה השנייה. ומצאו את הפתרון לשאלה.

 

 

---

3. מכונית יצאה משדה התעופה למרכז העיר. באותו זמן יצא אוטובוס ממרכז העיר לשדה התעופה. כאשר המכונית עברה חצי מהדרך לאוטובוס נשארו 19.2 ק"מ עד שדה תעופה, וכאשר אוטובוס עבר חצי מהדרך, למכונית נשארו 12 ק"מ עד מרכז העיר.

מה המרחק בין שדה התעופה למרכז העיר? 

כמה קילומטרים נותרו לאוטובוס עד סוף המסלול כאשר המכונית הגיעה למרכז העיר?

 

א. התאימו את הגרפים המתאימים לאוטובוס ולמכונית? מי מהם נוסע מהר יותר?

ב. אילו נקודות מציינות את אמצע הדרך של האוטובוס והמונית?

ג. איזה קטע המדובר בבעיה אורכו 19.2 ? איזה קטע אורכו 12?

ד. הראו כי הביעו את שוויון היחסים במשולשים אלה.
    מה מתאר יחס הדמיון?

ה. מצאו זוג נוסף של משולשים דומים. הביעו את שוויון היחסים במשולשים אלה.

ו. השוו בין היחסים (של הסעיפים ד' ו-ה') ומצאו את המרחק בין מרכז העיר לשדה התעופה.

ז. השלימו את הגרפים עד להגעת המכונית למרכז העיר. 

    מצאו בדרך דומה כמה קילומטרים נותרו אז לאוטובוס עד ליעדו.

 

 

 

 

דרך פתרון נוספת: נסמן את הזמן של אמצע הדרך של המכונית ב-t, ונביע בעזרתו את המהירויות של המכונית והאוטובוס. נשווה בין הזמן של המכונית והאוטובוס כאשר זה הגיע למחצית הדרך.

---

במבט על - פעילות אינטרקטיבית מקסימה כמבוא לגרף המתאר תנועה.

---

פעילות הרחבה- "מרוץ מכוניות דינאמי" בו הפנייה לסימולציה של בעיית תנועה, למאמר העוסק בסגנונות למידה שונים,
ובעיות תנועה רבות בספר האלקטרוני "לראות מתמטיקה- פונקציות" של מטח.

---

 

תקציר| פחות או יותר| פתרונות

 1.  האוצר

חבורת "כח המח" מצאה בשיטוטיה, שק ובו אוצר של מטבעות זהב וכסף. הם העריכו שמשקלו לא יותר מ-1 ק"ג. כל מטבע זהב שוקל כ-10 גרם וכל מטבע כסף שוקל כ-5 גרם.
כמה מטבעות מכל סוג ייתכנו בשק?

א. סמנו את מספר מטבעות הכסף ב- x ואת מספר מטבעות הזהב ב- y.
    הביעו באמצעות x ו- y את משקל המטבעות בשק.

ב. אילו מהביטויים הבאים מתארים את הערכת המשקל של שק המטבעות.

ג. לפניכם גרף המתאר את משקל שק המטבעות.

1.  כמה מטבעות בשק אם היו רק מטבעות זהב? רק מטבעות כסף?
     סמנו נקודות אילו בגרף.

2. מה מספר מטבעות הזהב ומטבעות הכסף האפשריים כך שמשקל השק הוא בדיוק 1 ק"ג.
    סמנו נקודות אילו בגרף. מה מאפיין אותן?

3. תנו כמה דוגמאות לתכולת שק שמשקלו יותר מ-1 ק"ג.
    סמנו נקודות אילו בגרף. היכן נמצאות הנקודות ביחס לישר?

4. תנו כמה דוגמאות לתכולת שק שמשקלו פחות מ-1 ק"ג.
    סמנו נקודות אילו בגרף. היכן נמצאות הנקודות ביחס לישר?

שרטוט גרף לאי שוויון לינארי

1. שרטטו ישר המתאים לשוויון. השתמשו בקו רציף כאשר אי השוויון הוא של קטן/גדול ושווה,
    ובקו מרוסק כאשר אי השוויון הוא קטן/גדול ממש.

2. הישר ששרטטתם מחלק את המישור לשני חצאים. 
    בחרו נקודת מבחן כלשהי באחד החצאים ובדקו האם היא מקיימת את אי השוויון.

3. אם נקודת המבחן מקיימת את אי השוויון הצלילו את כל חצי המישור בו היא נמצאת. 
    אם לא הצלילו את חצי המישור השני.

2.  במגרש הכדורסל 

נותרו עוד שתי דקות לשריקת הסיום במשחק הכדורסל.
קבוצתכם בפיגור של 12 נקודות. 
באפשרותכם לקלוע זריקות של 3 נקודות ושל 2 נקודות בלבד. 

מהן האפשרויות שלכם לזריקות לסל כדי לזכות בלפחות 12 נקודות ?

א. סמנו את מספר הקליעות של 2 נקודות ב- x ואת מספר הקליעות של 3 נקודות ב- y. הביעו באמצעות x ו- y את מספר הנקודות האפשרי ורשמו את אי השוויון המתאים.

ב. שרטטו במערכת הצירים גרף לאי השוויון. סמנו בגרף נקודות העונות על תנאי השאלה. זכרו מספר הקליעות הוא מספר שאינו שלילי ושלם.

3.  ארוחת בוקר בריאה 

עליכם לתכנן תפריט לארוחת בקר בריאה שתכיל לכל היותר 500 קלוריות, ע"פ הטבלה הבאה:

א. בחרתם כוס מיץ עגבניות, דגנים וחלב. איזו כמות של דגנים וחלב תוכלו לכל היותר לקחת?

ב. בקר אחר בחרתם לאכול לחמנייה. איזו כמות של גבינה לבנה וכוסות מיץ תפוחים תוכלו לאכול?

ג. אם תרצו לאכול לחמנייה וביצה, כמה כוסות מיץ (תפוחים ועגבניות) תוכלו להוסיף?

ד. תכננו לכם ארוחת בקר נוספת.

יישומים אינטראקטיביים לשרטוט גרף לאי שוויון לינארי:

פתרון אי שוויון או מערכת אי שוויונות לינארית - ישום בעזרת Geogebra. (נדרש תוסף ג'אווה בדפדפן שאינו כרום)

פתרון מערכת אי שוויונות לינאריים באמצעות גרפים - יישום מבית 

פעילויות ומאמרים בנושא אי שוויונות לינאריים:

משוואות של אי-שוויונים ממעלה ראשונה במישור - מחר 98- התרת מערכות "או" ומערכות "וגם" של אי-שוויונים ממעלה ראשונה בשני משתנים, תוך התייחסות לצורת תחום הפתרון. זוהי הקדמה לחוברת "תכנון לינארי - מושגים, שיטות, יישומים - לימוד בשילוב מחשב".

לביצוע המטלות ניתן להעזר בכל תוכנת מחשב המאפשרת חקירת פונקציות ו/או במחשבון גרפי.

התרת אי-שוויון ומערכת אי-שוויונים ממעלה ראשונה- מחר 98- דפי עבודה לתלמיד בנושא: הפונקציה הקווית, המשלבים את המחשב בלימוד הנושא. דפים אלה הם חלק מחוברת הנקראת "שילוב המחשב בלימוד המתמטיקה - הפונקציה הקווית. הדפים בנויים בצורה של גילוי של תכונות הפונקציה, ע"י העלאת השערות ובדיקתן של דוגמאות רבות במחשב. בנוסף לכל דף עבודה לתלמיד, יש דף למורה המכיל המלצות למורה וכן הפניה לנספח.

תקציר|יצירת מגן דוד|

בעזרת סרגל ומחוגה תוכלו ליצור עיצובים מרהיבים של מגן דוד, באופן הבא:

1) שרטטו מעגל בעזרת מחוגה. 

    שימרו על מרחק בין שתי רגלי המחוגה עד לשלב הבא.

2) סמנו נקודה. על המעגל , העמידו את חוד המחוגה על הנקודה שסימנתם וסמנו נקודה נוספת על המעגל.

   חזרו על פעולה זו  מספר פעמים עד שתקבלו שש נקודות על הקף המעגל.

   מדוע יש בדיוק שש נקודות? 

3) חברו כל נקודה עם שתי נקודות שנמצאות ממולה (החיבור נעשה לסירוגין בין הנקודות שסימנתם על הקף המעגל). 

    קיבלתם מגן דוד, שמו המתמטי הקסגרם.

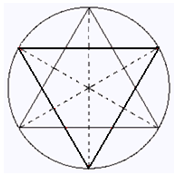
4) שרטטו בעזרת סרגל שלושה קטרים מקווקווים. (בהמשך תמחקו אותם)

5) ציירו שני משולשים שקודקודם בנקודות המפגש הקטרים עם צלעות המשולשים הגדולים.

    קיבלתם מגן דוד פנימי קטן.

6) כעת תוכלו להדגיש את הקווים שברצונכם בכדי ליצור את המגן דוד המעוצב.

    לפניכם שלש צורות שיוכלו להיות בסיס ליצירתכם.

    צבעו את חלקי המגן דוד כרצונכם.

    התוכלו למצוא עיצובים נוספים למגן הדוד?

על בסיס אותו רעיון תוכלו לצייר מגו דוד בתוך מגן דוד בתוך מגן דוד...עוד ועוד.

מקור:  http://www.mathcats.com/crafts/hexagrams.html

קישורים נוספים לחקר צורת מגן הדוד והצעות לפעילות:

"מגן דוד", במונחים מתמטיים ידוע כהקסגרמה, הוא המוטיב המרכזי בדגל ישראל ולו תכונות מתמטיות מרתקות. 

בקישורים הבאים תוכלו להעמיק וללמוד על תכונותיו המעניינות, על מקורותיו וההסטוריה המגוונת שלו בתרבויות השונות, והמשמעויות השונות שהעניקו לו. תוכלו גם להתרשם מאוסף עשיר של יצירות מגני דוד בציורי קיר, איורים, תחריטים, פסיפסים ופסלים.

מגן דוד - מידע תמציתי בויקיפדיה.

גיאומטריה של מגן-דוד - בעיית החודש מס' 5 - קשר חם.

חומשי - עיתון לעידוד המתמטיקה פרי עטו של ג'רי רוזן ז"ל המוקדש כולו למגן דוד. שם תמצאו מידע ופעילויות, חידות , הצעות ליצירה, קיפולי נייר ועוד.

אלבום מגן דוד - בלוג עשיר מאין כמוהו של זאב ברקן ובו מידע על מקורו, עברו, המשמעויות השונות שמיוחסות לצורתו של המגן דוד בתרבויות השונות. באתר אוסף עצום של תמונות ויצירות של מגני דוד.

מצגת מגן דוד והדגל - בעריכת אסף פלר.

יצירות ואיורים של מגני דוד בהשראת מתמטיקה מתחרות שנת השישים מטעם מרכז המורים במתמטיקה.

רימון, מגן דוד ומתמטיקה - מצגת שנוצרה בביה"ס "אורט במעלה" טבריה, במסגרת תחרות "תמונה ישראלית בעין מתמטית"

תקציר|אנשי החידות מהודו | פתרונות

בהודו העתיקה, בשנים 1200-200 לספירה, הייתה פריחה של יצירה עשירה במתמטיקה ובמדעים. 

הם פיתחו את נושא הגיאומטריה והטריגונומטריה לצרכי חישובים אסטרונומיים, הם פיתחו שיטות לפתרון משוואות דיופנטיות אך עיקר תרומתם הייתה יצירת המספר העשרוני, שיטת הספירה שאנו משתמשים בה עד היום. הם סימנו לראשונה את המספר "אפס" והיו גם הראשונים

לקבל את המספרים השליליים.

המתמטיקאים ההודיים הידועים ביותר הם: אריבסהטה הראשון מהמאה ה-6 שחישב בדיוק רב את המספר פאי.ברהמהגופטה מהמאה ה-7, אשר עסק במשוואות דיופנטיות והידוע בזכות משפט המשמש לחישוב שטחו של מרובע החסום במעגל לפי צלעותיו. בהסקרא השני מהמאה

ה-12 אשר עסק בפתרון משוואה ריבועית.

תרומתם של המדענים ההודים בחשבון ובאלגברה השפיעה רבות על התפתחות המתמטיקה בארצות הערב ולאחר מכן בארצות אירופה.

לפניכם כמה חידות עתיקות שהציגו המתמטיקאים ההודים העוסקות דווקא במשפט פיתגורס היווני:

1. עץ הצפצפה הבודד

על גדות נהר הגנגס צמח עץ צפצפה בודד.

לפתע הגיע משב רוח חזק וכפף את גזעו של העץ. 

נשבר העץ  המסכן וצמרתו נפלה על הגדה הנגדית של הנהר שרוחבו 4 מטרים.  גזע העץ הגאה, באורך 3 מטרים, נותר לעמוד מאונך לזרם הנהר.

התוכלו לדעת מה היה גובהו של העץ לפני שהרוח שברה אותו?

2. פרח הלוטוס הקדוש

פרח הלוטוס מקודש על הבודהיסטים, שלפי אמונתם פרץ הצמח ופרח בכל מקום עליו דרכו רגליו של הנסיך התינוק סאדהראתה (בעתיד בודהה). תחת שורשיו הנטועים עמוק בביצה שוכנים אוצרות. 

באגם שקט צמח פרח מרהיב של הלוטוס הקדוש. שורשיו של הצמח עמוק בקרקעית האגם והפרח התנשא כחצי מטר מעל פני המים. הוא היה פרח יחיד וכשרוח נשבה נישא הפרח על פני המים ונעלם רק באביב המוקדם מצא אותו דייג במרחק של שני מטרים מהמקום שבו הפרח

גדל.

התוכלו לדעת מה עומקו של האגם בו צמח הלוטוס?

3. ירושת האיכר

איכר הודי  עשיר וחובב מתמטיקה הוריש לשלושת בניו את חלקתו הריבועית.

האיכר סימן על אחת מצלעות המגרש את אמצעו (E) ומתח קו עד לנקודה כלשהי על הצלע שממול (F). 

הבן הצעיר קיבל חלקה בתוך המגרש בצורת משולש אשר שטחו 9 דונם.

את שתי החלקות הנותרות הוריש לשני בניו הבכורים התאומים.

מהי הנקודה (F) שבחר האיכר כך ששטחי חלקות הבנים התאומים היו שווים?

4. המנזר הבודהיסטי

כל יום יצא האיכר ההודי מביתו (A) לתפילת הבקר במנזר ((B.

הוא הלך בקצב מתון ומדוד בעודו ממלמל את אותה שירה בכל יום ויום.

לעיתים היה עושה את דרכו דרך המעיין הקדוש (C) ולעיתים עבר דרך הנהר (D). 

התוכלו להביע את הדרך מבית האיכר לנהר (AD=d) לפי הדרך מבית האיכר למעיין (AC=a)

ומן המעיין עד המנזר (CB=b)?

מהי התשובה הנכונה?

הפיצוח נכתב ע"י נטליה קונצ'יקוב במסגרת קורס כתיבה יצירתית במתמטיקה

תקציר |מתמטיקה מכל הלב | פתרונות | رياضيات من القلب | حلول | ערבית| פתרונות בערבית

למסיבת סוף השנה אפו התלמידים חמש עוגות בצורת לב.

א. הסבירו כיצד נבנתה התבנית של כל עוגה.

ב. חשבו את השטח של כל עוגה, כאשר ידוע שהקטע המסומן אורכו 10 ס"מ. מהי העוגה הגדולה ביותר ?

ג. פי כמה יגדל שטח כל "לב", אם נכפיל את בסיס התבנית (הקטע המסומן) פי 2?

ד. אם נסמן את בסיס התבנית ב-a, הביעו את שטח כל לב באמצעות a.

עוד לבבות מתמטיים תוכלו למצוא - http://www.mathematische-basteleien.de/heart.htm

משימת אתגר- האם תוכלו לשרטט לכם לב מגרפים של פונקציות?

קחו לכם פתק ריבועי וקפלו לב לבבי.

עקבו אחר ההוראות באיור ובסרטון הבא :

התבוננו בלב שקיבלתם:

א. מצאו חלוקות שונות של הלב למצולעים שונים.
ב. איזה חלק של הריבוע מהווה הלב.

תקציר| פחות או יותר

1.  בבוסתן 

לפניך מפת בוסתן פירות ישראלי.

כל חלקת עצים מגודרת. עליך להגדיר עבור מערכת ההשקיה את התחום בו כל חלקה נמצאת.

א. רשמו מערכת אי שוויונות המתארת את שטח עצי התפוח. 
ב. איזה שטח מתואר ע"י אי השוויונות הבאים: 

ג. רשמו מערכת אי שוויונות המתארת את שטח עצי הזית.

ד. הוכיחו כי שטח עצי הזית שווה לשטח כל עצי הפירות האחרים.

2.  עבודה בחופשת הקיץ 

הקיץ החליטה הילה לעבוד בחופשת הקיץ בכדי לחסוך לטיול "מחוף אל חוף".  
הילה מתכוונת לעבוד לא יותר מ-20 שעות בשבוע (בכדי שתספיק גם לנוח ולבלות) ובכל זאת להרוויח לפחות 360 שקל לשבוע העבודה. 
להילה שתי הצעות עבודה: שמרטפית ושוטפת כלים במסעדה. 
עבור שעת העבודה בשמרטפות משלמים 20 שקל ועבור שטיפת כלים 24 שקל לשעה.

א. אם הילה תעבוד רק בשמרטפות או רק בתור שוטפת כלים, כמה היא תרוויח?

ב. אם הילה תחלק את שעות העבודה בין שמרטפות לבין שטיפת כלים שווה בשווה, 
כמה היא תרוויח?

ג. הציעו להילה חלוקה כזאת של שעות עבודה, כך שהיא תחסוך סכום כסף הגדול ביותר האפשרי.

3.  משחק כדורסל

ארז חזר ממשחק כדורסל וסיפר בגאווה למשפחתו על המשחק:
"היו לי 10 כדורים חוזרים, 2 חסימות ו-3 התקפות מתפרצות והכי חשוב.. הצלחתי לקבל מספר נקודות שלא קטן ממספר הנקודות הגבוה ביותר שהיה לי בעונה הקודמת".
ארז, חובב החידות, סרב לחשוף כמה נקודות קלע אך רמז:

(1) לא זרקתי אף קליעת עונשים. (עבור קליעת עונשין מקבלים נקודה אחת). 
(2) מספר הסלים של 2 נקודות קטן או שווה ל-8. 
(3) מספר הסלים של 2 נקודות היה גדול מפעמיים ממספר הסלים של השלשות (עבור שלשה מקבלים 3 נקודות).
(4) מספר הנקודות הגבוה ביותר בעונה שעברה היה 18.

ננסה לעזור למשפחתו של ארז לגלות מהו מספר הנקודות שקלע:

א. סמנו: ב-x את מספר הסלים של 2 נקודות וב-y את מספר הסלים של 3 נקודות.
הביעו באמצעות x ו- y את הרמזים של ארז.

ב. שרטטו במערכת צירים בה  ו-  (מדוע?), את הישרים המתאימים לרמזים (2) ו-(3). סמנו את כל הנקודות ששיעוריהן מקיימים את הרמזים הללו.

ג. הוסיפו למערכת הצירים גם את הישר המתאים לרמז האחרון.
סמנו את כל הנקודות ששיעוריהן מקיימים את כל הרמזים של ארז.

ד. מהו המספר הגדול ביותר של הנקודות שיכול היה לקבל ארז?

 4. אימון כושר ושריפת קלוריות

באימון שחייה ניתן לשרוף 12 קלוריות בדקה ואילו ברכיבה על אופניים ניתן
לשרוף 8 קלוריות בדקה.
דנה החליטה לשלב באימון את שתי הפעילויות הספורטיביות.

א. סמנו את מספר דקות השחייה ב-x, ואת מספר דקות רכיבה באופניים ב-y.
    רשמו ביטוי למספר הקלוריות שנשרפות באימון המשלב שחייה ורכיבת אופניים.

ב. כמה קלוריות תשרוף דנה באימון של 30 דקות בשחייה בלבד ?
    ברכיבה באופניים בלבד? 
    אם תחלק את זמן האימון שווה בשווה בין שחייה ואופניים?

ג. דנה החליטה להתאמן לכל היותר 30 דקות כך שתשרוף לפחות 300 קלוריות.
   הציעו לדנה תוכנית אימונים מתאימה. 

ד. דנה חייבת לרכב על האופניים לפחות 10 דקות באימון ובשאר האימון לשחות. מהו המספר המרבי (מקסימלי) של קלוריות אותו תוכל לשרוף?

יישומים אינטראקטיביים לשרטוט גרף לאי שוויון לינארי:

פתרון אי שוויון או מערכת אי שוויונות לינארית - ישום בעזרת Geogebra.

פתרון מערכת אי שוויונות לינאריים באמצעות גרפים - יישום מבית 

פעילויות ומאמרים בנושא אי שוויונות לינאריים:

משוואות של אי-שוויונים ממעלה ראשונה במישור - מחר 98- התרת מערכות "או" ומערכות "וגם" של אי-שוויונים ממעלה ראשונה בשני משתנים, תוך התייחסות לצורת תחום הפתרון. זוהי הקדמה לחוברת "תכנון לינארי - מושגים, שיטות, יישומים - לימוד בשילוב מחשב.

לביצוע המטלות ניתן להעזר בכל תוכנת מחשב המאפשרת חקירת פונקציות ו/או במחשבון גרפי.

התרת אי-שוויון ומערכת אי-שוויונים ממעלה ראשונה- מחר 98-  דפי עבודה לתלמיד בנושא: הפונקציה הקווית,  המשלבים את המחשב בלימוד הנושא. דפים אלה הם חלק מחוברת הנקראת "שילוב המחשב בלימוד המתמטיקה - הפונקציה הקווית. הדפים בנויים בצורה של גילוי של תכונות הפונקציה, ע"י העלאת השערות ובדיקתן של דוגמאות רבות במחשב. בנוסף לכל דף עבודה לתלמיד, יש דף למורה המכיל המלצות למורה וכן הפניה לנספח.