תקציר|![]() גלו את ההוכחה|
גלו את ההוכחה|![]() חומר למורה
חומר למורה
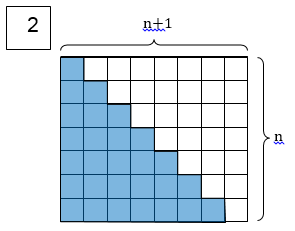
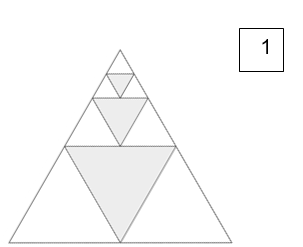
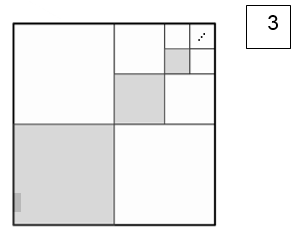
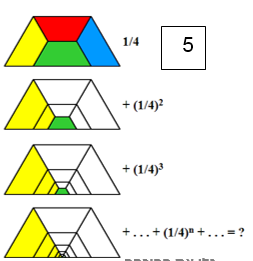
בכל אחד מן הסרטוטים מסתתרת הוכחה לנוסחה הקשורה לסכומי סדרות.
גלו את ההוכחה המסתתרת בכל סרטוט.
| |
|
 |
 |
 |
 |
 |
 |
בדיוק או בערך
בחרו את התשובה המדויקת ביותר בעיניכם
1.
א. . ב. קצת יותר מ-
. ג. . קצת פחות מ-
. ד. מתלבט/ת
א. 1. ב. קצת יותר מ- 1. ג. קצת פחות מ- 1 . ד. מתלבט/ת.
תקציר| ![]() היכן לקנות את הפיצה?|
היכן לקנות את הפיצה?|![]() חומר למורה
חומר למורה
1. בפסטיבל מדברי גדול התמקמו שתי פיצריות במרחק 6 ק"מ זו מזו, והן מספקות על גמלים פיצות לכל דורש. הפיצריות זהות בתפריט, באיכות ובמחיר הפיצה, וכל אחת מהפיצריות גובה שקל אחד לק"מ דמי משלוח.
א. היכן תקנו את הפיצה (התייחסו למקומות שונים בהם אתם יכולים להימצא?
ב. היכן נמצא קו פרשת הפיצה – קו התפר בין האזור שבו עדיף לקנות מפיצרייה א לבין האזור בו עדיף לקנות מפיצרייה ב?
ג. תוכלו לחקור את הבעיה באמצעות היישומון היכן לקנות את הפיצה. קבעו את יחס המחירים בין הפיצריות ל- m=1. תוכלו להגדיל ולהקטין את המרחק מהפיצרייה השנייה (). כדי לראות היכן נמצאות כל נקודות החיתוך בין העגלים, השתמשו באופציה "הפעל עקבות".
2. כיצד ישתנה קו התפר בין אזורי השיווק של הפיצריות, אם פיצרייה א תמשיך לגבות 1 ₪ לק"מ דמי משלוח ואילו פיצרייה ב תעלה את דמי המשלוח ותגבה 2 ₪ לק"מ דמי משלוח?
כדי לחקור אפשרות זו שנו את היחס בין מחירי המשלוח ל- m=2. בהתאם ישתנה גם היחס בין הרדיוסים של המעגלים (מדוע?)
3. אתם מוכנים להמשיך ולחקור את הבעיה לכל בין דמי המשלוח, וכן למצוא את הפתרונות גם בדרך אלגברית. לנוחיותכם, וכדי שהפתרון שלכם יתאים ליישומון, מקמו את הפיצרייה המשנה מחירים בראשית הצירים, ואת הפיצריה הגובה שקל אחד לק"מ מקמו בנקודה (6,0).
תקציר|![]() צביעת שני משולשים|
צביעת שני משולשים|![]() חומר למורה
חומר למורה

א. נצבע את המשולש החל מקודקוד A, עם משולש ישר זווית דומה לו (ADE) כאשר הנקודה D נעה על הצלע AB.
נסמן את אורך AD=x
הזיזו ביישומון את הנקודה D, ותארו כיצד משתנה השטח הצבוע כאשר x משתנה.
נגדיר פונקציה S(x) המתאימה ל- x את השטח הצבוע. האם פונקציית השטח הצבוע עולה? תארו את קצב ההשתנות שלה.

נצבע את המשולש החל מקודקוד B', עם טרפז (B'C'LK) כאשר הנקודה K נעה על הצלע A''B.
נסמן את אורך B'K'=x
הזיזו ביישומון את הנקודה D, ותארו כיצד הפעם משתנה השטח הצבוע כאשר x משתנה.
האם פונקציית השטח הצבוע עולה? תארו את קצב ההשתנות שלה.
ג. תארו מתי השטחים הצבועים בשני המשולשים יהיו שווים.
ד. חשבו את השטחים הצבועים בשני המשולשים, כאשר D אמצע הקטע AB ,
ו- K אמצע הקטע A'B' .
ה. חשבו את השטחים הצבועים בשני המשולשים, כאשר X=2.
ו. היעזרו ביישומון לשם חישוב השטחים ומלאו את הטבלה:
| X=6 | X=5 | X=4 | X=3 | X=2 | X=1 | X=0 | |
| שטח צבוע במשולש 1 | |||||||
| שטח צבוע במשולש 2 |
ז. עקבו ביישומון אחר בניית הגרף המתאר את השתנות השטח הצבוע כפונקציה של x, בכל אחד מהמשולשים.
במה דומים ובמה שונים שני הגרפים?
ח. שערו כיצד נראה גרף הנגזרת של פונקצית השטח בכל אחד מהמקרים?
ט. רשמו פונקציה המתארת את השתנות השטח הצבוע כאשר x משתנה עבור כל אחד מהמשולשים. הקלידו בחלון הקלט ובדקו תשובתכם.
גזרו את הפונקציה ובדקו השערתכם.





