לפניכם גרף המתאר התפרקות אופיינית של האינסולין בדם מהרגע שנלקחה התרופה.
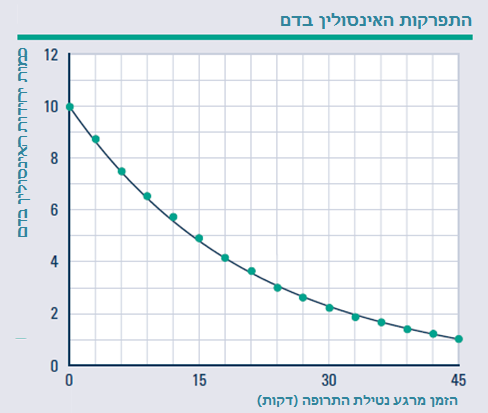
1. השלימו את הטבלה:
2. תארו במילים את התפרקות האינסולין בדם כתלות בזמן. תארו את קצב השינוי.
3. בהתבסס על הגרף והטבלה איזו פונקציה מתארת התפרקות האינסולין בדם כתלות בזמן?
4. חשבו על פי הפונקציה ובדקו בגרף.
א. כמה אינסולין נותר בדם לאחר שעה?
ב. כמה יחידות אינסולין בדם לאחר שעה וחצי?
ג. לאחר כמה זמן נותר בדם חצי מהכמות ההתחלתית של האינסולין?
ד. לאחר כמה זמן נותר בדם חצי יחידה של אינסולין?
בפתרון השאלות הבאות תוכלו להיעזר ביישומון:
1. ד"ר פאר רשם לחולה מסויים כדורי טריאזולם. לאחר שהחולה נטל מספר גלולות,
היתה בדם של החולה כמות התחלתית של 4 מיליגרם.
א. מה תהיה כמות הסם בדם לאחר שעה? לאחר 6 שעות? לאחר יממה?
ב. במשך כמה שעות תעלם השפעת הסם ?
ג. בדיקת דם מסוגלת לאבחן נוכחות של התרופה אם תמצא בדם כמות של לפחות 0.1 מיליגרם מהתרופה.
לאחר כמה זמן תתקבל בדיקה שלילית?
2. א. שרטטו גרף לכל תרופה.
ב. השוו את השפעת ארבעת הסמים וסכמו את מסקנותיכם בכל ייצוג שתבחרו. מה ניתן לומר על קצב ההתפוגגות של כל תרופה.
ג. רק שלש מן הגלולות הן אמיתיות, הצביעו על גלולת השינה הלא אמיתית ונמקו תשובתכם.
3. רופאים מתעניינים בזמן שלוקח לתרופה בדם להגיע לחצי מהכמות ההתחלתית שניטלה. זמן זה נקרא מחצית החיים.
חשבו מהו זמן מחצית החיים של כל תרופה.
הפעילות מעובדת מתוך – פעילויות חקירה תמוכות מחשב – פונקציה מעריכית ולוגריתמית – אוניברסיטת חיפה.
מקורות נוספים:
הסכנות באקמול – שיעור אינטראקטיבי לחקר השאלה מה קורה שלוקחים תרופת האקמול לכאב ראש בכמויות שונות ובזה אחר זה.
יישומונים ופיצוחים בנושא גידול ודעיכה:
אני ואתה נשנה את העולם – פיצוח העוסק בפונקציה המעריכית דרך סרט הקולנוע "העבר את זה הלאה".
דעיכה רדיואקטיבית - סימולציה לדעיכה רדיואקטיבית. ישומון דינאמי ודף עבודה בו ניתן לחקור כיצד משפיעים הפרמטרים השונים של פונקצית הדעיכה על הגרף הן בייצוג הגרפי, הטבלאי והויזואלי. כמו כן ניתן לעקוב אחר ערכים של הפונקציה.וכן להתרשם מקצב הדעיכה באנימציה של המיכל המתרוקן.
מרוב עצים לא רואים את היער...סימולציה לגידול מעריכי של יער ישומון דינאמי ודף עבודה בו ניתן לחקור כיצד משפיעים הפרמטרים השונים של פונקצית הגידול על הגרף הן בייצוג הגרפי, הטבלאי והויזואלי. כמו כן ניתן לעקוב אחר ערכים של הפונקציה .וכן להתרשם מקצב הגידול באנימציה של היער הגדל.
עלייה במחירי הדירות – הפעילות כוללת דף עבודה ויישומון דינאמי, ועוסקת בהשוואה בין עליה של המחירים של שתי דירות בגידול מעריכי.
תקציר|![]() פירמידה משולשת|
פירמידה משולשת|![]() מדריך למורה
מדריך למורה
במבט נוסף על בחינת הבגרות – 807 – חרף תשע"ז – שאלה 2
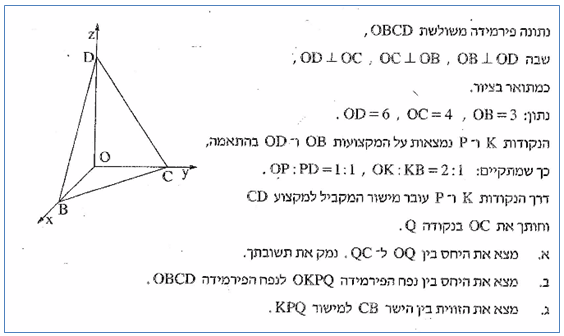
נתונה פירמידה משולשת OBCD, קדדקוד O בראשית הצירים , והקדקודים B,C,D נמצאים על הצירים x,y,z בהתאמה.
א. רשמו על פי הנתונים את שיעורי הקדדקדים של הפירמידה.
ב. חשבו על פי חלוקת היחסים הנתונים את שיעורי הנקודות P, K.
בדקו את חישובכם ביישומון. הפעילו את הכלי "סיבוב הצגה תלת מימדית" בכדי להתרשם מהפירמידה במבטים שונים.
ג. דרך הנקודות K ו-P העבירו מישור המקביל למקצוע CD, וחותך את OC בנקודה Q. הציגו ביישומון את המישור המקביל והתבוננו בו במבטים שונים.
הסבירו מדוע PQ מקביל למקצוע CD. (תוכלו להיעזר בחלון הימיני התחתון)
ד. התבוננו במשולש OCD, מה ניתן לומר על הקטע PQ ?
ה. חשבו את היחס בין OQ ל-QC. נמקו תשובתכם.
מהם שיעורי הנקודה Q ?
ו. חשבו את יחס הנפחים.
ומה יקרה אם....
א. אם נזיז את הנקודה K ,
- האם וכיצד ישתנו שיעורי הנקודה Q ?
- האם המישור PQK עדיין מקביל ל-CD ?
- כיצד ישתנה יחס הנפחים?
ב. אם נזיז את הנקודהP ,
- האם וכיצד ישתנו שיעורי הנקודה Q ?
- האם המישור PQK עדיין מקביל ל-CD ?
- כיצד ישתנה יחס הנפחים?
ג. האם תוכלו להצביע על הבדל בין ההשפעה של השינוי במיקום הנקודה K ל נפח הפירמידה, לבין ההשפעה של השינוי במיקום הנקודה P על נפח הפירמידה?
ד. האם תוכלו לקבוע את הנקודות K ו-P כך שיחס הנפחים יהיה ? ? ?
אם לא, הסבירו מדוע. אם כן, כיצד? נמקו.
תקציר|![]() אל הפונקציה צעד אחר צעד|
אל הפונקציה צעד אחר צעד|![]() מדריך למורה
מדריך למורה
אל משפחת הפונקציות
א. נבחן צעד אחר צעד את שלבי הבנייה של משפחת הפונקציות , בעזרת פעולות והרכבה של פונקציות שונות.
לגבי כל אחת מהפונקציות הבאות, בכל שלב ענו, אם ניתן ללא שימוש בנגזרת. שימו לב, במעבר משלב לשלב אילו תכונות השתנו? אילו נשמרו?
| איזו פעולה הופעלה במעבר מהפונקציה הקודמת ? | מהו תחום ההגדרה? | אסימפטוטות מאונכות לצירים | האם הפונקציה זוגית? אי זוגית? |
תחומי חיוביות ושליליות | תחומי עליה וירידה | סקיצה לגרף הפונקציה | סקיצה לגרף כאשר a=0 | ||
| 1 | XXXXX | ||||||||
| 2 | |||||||||
| 3 | |||||||||
| 4 |
ב. חקרו, את משפחת הפונקציות , צעד אחר צעד, באופן דומה לחקירה בסעיף א
ג. חשבו את הנגזרת של הפונקציה .
חקרו את משפחת הפונקציות , באופן דומה לחקירה שביצעתם בסעיף א.
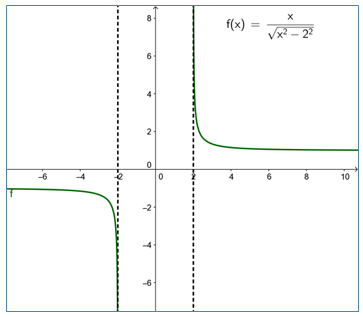
כאשר a=2.
1. סמנו על הגרף את השטח המתואר ע"י הביטוי
2. סמנו על הגרף את השטח המתואר ע"י הביטוי
3. מצאו עבור את ערך הביוטי:
ה. מצאו, עבור , את ערך הביטוי
אם הפונקציה היא:
1.
2.
תוכלו לבדוק את תשובתכם ביישומון סכום אינטגרלים.
ו. ללא חישובים מספריים הביאו דוגמה לפונקציה נוספת כך שעבור ערך הביטוי
יהיה אפס.
תוכלו לבדוק את הדוגמה שלכם ביישומון סכום אינטגרלים









