תקציר|![]() חסומים במעגל|
חסומים במעגל|![]() מדריך למורה
מדריך למורה
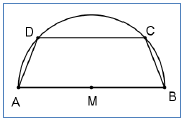
 נתון משולש PDC.
נתון משולש PDC.
הנקודות B ו- L מונחות על הצלע PC.
הנקודות A ו- K מונחות על הצלע PD.
נתון כי המרובע ABLK בר חסימה וגם המרובע KLCD בר חסימה.
חלק א
חקרו את המרובע ABCD על פי הסעיפים הבאים, והסבירו את תשובותיכם:
אפשר להיעזר ביישומון
1. האם ABCD מקבילית? תמיד/ לפעמים/ אף פעם לא?
2. האם ABCD דלתון? תמיד/ לפעמים/ אף פעם לא?
3. האם ABCD טרפז? תמיד/ לפעמים/ אף פעם לא?
4. האם ABCD טרפז שווה שוקיים? תמיד/ לפעמים/ אף פעם לא?
5. האם ניתן לחסום את המרובע ABCD במעגל? תמיד/ לפעמים/ אף פעם לא?
חלק ב
נהפוך את נקודת המבט:
ABCD טרפז. L נקודה על הצלע BC ו- K נקודה על הצלע AD. היעזרו ביישומון.
1. האם KABL מקבילית? תמיד/ לפעמים/ אף פעם לא?
2. האם KABL דלתון? תמיד/ לפעמים/ אף פעם לא?
3. האם המרובעים ABLK ו- KLCD ברי חסימה? תמיד/ לפעמים/ אף פעם לא? הסבירו.
4. האם יתכן שרק אחד מהמרובעים ABLK ו- KLCD בר חסימה? הסבירו.
תקציר|![]() עבודת שורשים|
עבודת שורשים|![]() מדריך למורה
מדריך למורה
בעקבות בחינת הבגרות לתלמידי 4 יחידות – 35481 – קיץ תשע"ו – מועד ב - שאלה 6
 חלק א
חלק א
לפניכם גרף הפונקציה
1. מהו תחום ההגדרה של הפונקציה ?
2. מצאו את נקודות הקיצון המוחלט של הפונקציה f וקבעו את סוגן.
3. מה הקשר בין תחום העלייה של הפונקציה h לבין תחום העלייה של הפונקציה f? נסו להסביר את תשובתכם ביותר מאשר דרך אחת.
4. סרטטו באותה מערכת צירים את גרף הפונקציה .
היעזרו בנקודות המסומנות באדום. האם לכל אחת מהן יש נקודה מתאימה על גרף הפונקציה f?
5. על גרף הפונקציה h מסומנות בירוק שתי נקודות ששיעור ה- y שלהן הוא 1. הסבירו מדוע נקודות אלה נמצאו גם על גרף הפונקציה f?
(רמז: מה הקשר בין מספרים קטנים מ- 1 לבין השורשים הריבועיים שלהם?)
חלק ב
נתונה הפונקציה
1.מהו תחום ההגדרה של הפונקציה g?
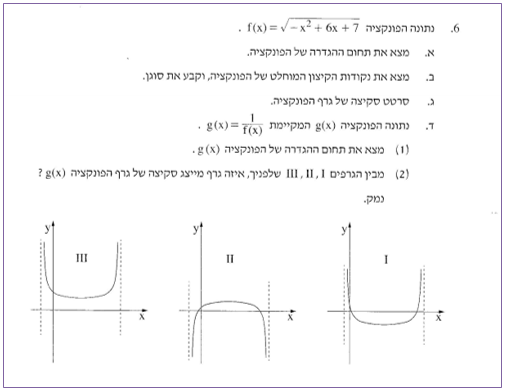
2. איזה מן הגרפים הבאים יכול לייצג סקיצה של גרף הפונקציה g? הסבירו.
חלק ג – סרטוט גרף של פונקציית שורש מורכבת בעזרת גרף הפונקציה הפנימית בלבד.
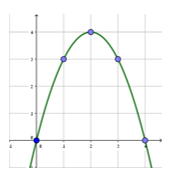
לפניכם גרף של פונקציה h.
נסרטט בעזרתו את גרף הפונקציה :
1. מהו תחום ההגדרה של הפונקציה f?
2. מצאו את נקודות הקיצון המוחלט של הפונקציה f וקבעו את סוגן.
3. מה הקשר בין תחום העלייה של הפונקציה h לבין תחום העלייה של הפונקציה f? נסו להסביר את תשובתכם ביותר מאשר דרך אחת.
4. סרטטו באותה מערכת צירים את גרף הפונקציה . היעזרו בנקודות המסומנות.
חלק ד – הרחבת החקירה לפונקציות נוספות מהמשפחה , כאשר h פונקציה ממעלה שנייה
היישומון שורשים מאפשר לסרטט גרפים של פונקציות שורש מורכבות, יחד עם פונקציה פנימית שהיא פונקציה ממעלה שנייה. משנים את הפרמטרים של הפונקציה הפנימית, והפונקציה המורכבת משתנה אף היא.
לנוחיות, נרשום את הפונקציה ממעלה שנייה בצורתה הקדקודית:
1. באיורים שלפניכם גרף הפונקציה הפנימית מופיע בקו רציף, וגרף הפונקציה המורכבת מופיע בקו מרוסק. מצאו באמצעות היישומון פונקציות שיכולות להתאים לאיורים:

(הגרף המקווקו הוא של הפונקציה המורכבת והגרף הרציף הוא של הפונקציה הפנימית)
היעזרו בסעיף 5 של חלק א'.
אוסף פעילויות זה מציג מספר בעיות קיצון מתפתחות. האוסף בנוי כמספר רצפי פעילויות, מלוות ישומונים לחקר והמחשה.
הפעילויות מיועדות לתלמידים ומבוססות על פעילויות מהספר "ללמוד וללמד אנליזה", שיצא לאור בשיתוף פעולה של המחלקה לחינוך למדע וטכנולוגיה בטכניון, מנהלת מל"מ ומשרד החינוך.
| רצף הפעילויות | מקום בתוכנית הלימודים | הפעילות | נושאים |
|
|
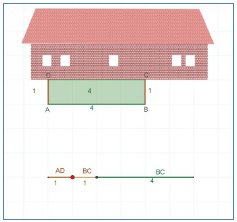
כיתה י' | חצר מלבנית |
חקירת פונקצית פולינום. מתאימה כפעילות פתיחה. |
| חצר פינתית | חקירת פונקצית פולינום | ||
| חצר מחולקת |
חקירת פונקצית פולינום, חקירת פונקציה עם פרמטר. (מתאים להצמחת הצורך בשימוש בפרמטרים) |
||
| עניין של מחיר |
חקירת פונקצית פולינום, חקירת פונקציה עם פרמטר.
|
||
|
|
כיתות י - י"א |
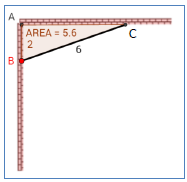
חצר משולשת | פונקצית שורש מורכבת. |
| משולש ישר זווית החסום במעגל |
חקירת פונקציות טריגונומטריות. אפשר לעקוף בדרך גאומטרית את השימוש בחקירת פונקציות טריגונומטריות. |
||
|
|
כיתות י - י"א |
חקירת פונקצית פולינום, חקירת פונקציה עם פרמטר. מגבלות התחום. |
|
|
|
כיתות י - י"א |
חקירת פונקציות שונות, חקירת פונקציה עם פרמטר. בחירת המשתנה החופשי חושפת תכונות מסויימות של התופעה. מערכים שונים לעבודה בקבוצות |