תקציר|כדאי להזיז את הפונקציה|מדריך למורה

נתונה הפונקציה .   a הוא פרמטר.

1. יעל הציעה לחקור פונקציה פשוטה יותר 

ובעזרת הזזות בלבד להסיק מסקנות לגבי הפונקציה הנתונה.

א. השלימו את הטבלה, תוכלו להיעזר ביישומון הדינאמי.

		a=0
תחום הגדרה:
אסימפטוטה אנכית:
אסימפטוטה אופקית:
נקודות הקיצון:
הגרף:

ב. ציינו מה דומה ומה שונה בין שתי הפונקציות? אילו תכונות  נשמרו ואילו תכונות השתנו וכיצד?

ג. כיצד תשתנה הפונקציה   כאשר נשנה את a ?
אילו תכונות  נשמרו ואילו תכונות השתנו וכיצד?

ד. עבור איזה ערך של a,  משיקה לציר ה-x ? נמקו.

2. נתונה הפונקציה    עבור a=1, k פרמטר.

לפניכם ארבעה גרפים שונים ממשפחת הפונקציות g(x). 

(בקו המקווקו מוצג גרף הפונקציה f(x)+k )

תוכלו להיעזרביישומון הדינאמי- הערך המוחלט של פונקציה מוזזת.

א. קבעו עבור אילו ערכי k ניתן לקבל כל אחד מהגרפים. נמקו.

ב. הוסיפו לגרפים את הישר שהוא האסימפטוטה של f(x). 
באילו מקרים גרף הפונקציה g(x) ישיק לישר זה? הסבירו.

תקציר|המקבילית|מדריך למורה

המרובע ABCD הוא מקבילית
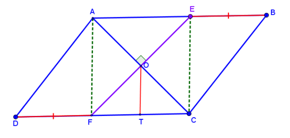
הנקודות E, F  מונחות על הצלעות AB, DC בהתאמה.
EB = FD 

ניתן להיעזר ביישומון המקבילית.

1. מה ניתן לומר על המרובע AECF ? הוכיחו טענתכם בדרכים שונות.

2. נתון גם כי

א. האם המרובע AECF מקבילית? תמיד/ לפעמים / אף פעם לא.

ב. האם המרובע AECF טרפז? תמיד/ לפעמים / אף פעם לא.

ג. האם המרובע AECF מעוין? תמיד/ לפעמים / אף פעם לא.

ד. האם המרובע AECF מלבן שאינו ריבוע? תמיד/ לפעמים / אף פעם לא.

ה. האם המרובע AECF מלבן ? תמיד/ לפעמים / אף פעם לא.

ו. האם המרובע AECF ריבוע ? תמיד/ לפעמים / אף פעם לא.

3. הראו כי שלש הנקודות B, O, D נמצאות על ישר אחד.

(רמז – הראו כי BD עובר דרך הנקודה O).

4. נתון גם: OT תיכון לצלע FC ב-

א. הוכיחו:

ב. שנו ביישומון את הזווית , כך שלא בהכרח תהיה ישרה.
האם עדיין נשמר הקשר    ?
נמקו.

5. מצאו כמה שיותר מצולעים בעלי שטחים שווים. 

תקציר|עץ פיתגורס|