תקציר|בעיות תנועה בדרך אחרת |פתרונות

1. אופניים וקטנוע יצאו מתל אביב באותה שעה. רוכב האופניים נסע במהירות של 20 קמ"ש ורוכב הקטנוע במהירות של 32 קמ"ש. כעבור שעה וחצי יצאה מאותו מקום באותו הכיוון מונית שעקפה את האופניים ולאחר חצי שעה השיגה גם את הקטנוע. באיזו מהירות נסעה המונית?

א. מה מתארים הישרים OB, OC ו- AC?
    מה מתארות הנקודות A, B, C ?

ב. מהי משוואת הישר המתארת את תנועת רוכב האופניים? מה מציין שיפוע הישר?

ג. מהי משוואת הישר המתארת את תנועת רוכב הקטנוע? מה מציין שיפוע הישר?

ד. נסמן את זמן המפגש של רוכב האופניים והמונית ב- t.
    מהם שיעורי הנקודות A, B, C, D, E ,F.

ה. הביעו את מהירות המונית כפונקציה של t .

ו. הביעו את מרחק הנסיעה של המונית עד לנקודת המפגש עם הקטנוע בשני אופנים:

    1. לפי נוסחת המרחק (מכפלת הזמן במהירות).

    2. כסכום של שני מרחקים CE=CF+FE. (הסבירו)
        השוו בין שני הביטויים ומצאו את t.

דרך פתרון נוספת באמצעות השוואת ביטויים למהירות המונית בקטעי זמן שונים.

או באמצעות דמיון המשולשים   (ראו הדרכה לבעיה 3)

---

2.  דני ודינה יצאו להליכה באותו זמן, זה לקראת זו .

דני יצא מביתו במעלה אביב ודינה יצאה מביתה שבמעלה הסתוונית. הם חלפו זה על פני זו  והמשיכו בדרכם עד ליעדם, (דני למעלה סתוונית ודינה למעלה אביב) ומיד החלו לחזור אל הישוב ממנו באו. עד פגישתם השנייה (כשהלכו בחזרה) דינה עברה  שישה

קילומטרים יותר מדני.  דינה הגיעה בחזרה לביתה שעה אחרי פגישתם השנייה ואילו דני הגיע לביתו שעתיים וחצי אחרי פגישה זו.

מצאו את המהירויות של דני ודינה ואת המרחק בין הישובים.

 

במערכת הצירים הבאה מתוארים שני המסלולים של דני ודינה:

א. התאימו את הגרפים המתאימים לדרכם של דינה ודני ? מי הולך מהר יותר ?

ב. תארו במילים מה מתארות כל הנקודות המסומנות בגרף. (פרט ל-H ו-F).

ג. תארו במילים מה מתארים אורכי הקטעים AB, CF ו- HC .

ד. נסמן את אורך הקטע CF ב-d . הביעו באמצעות d את אורכי הקטעים HC ו- AB .

ה. תארו במילים מה מתארים הקטעים FD ו- HG . מהם אורכם ? 

ו. הביעו את המהירויות של דינה ושל דני באמצעות d.

ז. הביעו את הדרך שעבר כל אחד מהם עד לפגישה השנייה.

ח. השוו בין זמני ההליכה של דני ודינה עד לפגישה השנייה. ומצאו את הפתרון לשאלה.

 

 

---

3. מכונית יצאה משדה התעופה למרכז העיר. באותו זמן יצא אוטובוס ממרכז העיר לשדה התעופה. כאשר המכונית עברה חצי מהדרך לאוטובוס נשארו 19.2 ק"מ עד שדה תעופה, וכאשר אוטובוס עבר חצי מהדרך, למכונית נשארו 12 ק"מ עד מרכז העיר.

מה המרחק בין שדה התעופה למרכז העיר? 

כמה קילומטרים נותרו לאוטובוס עד סוף המסלול כאשר המכונית הגיעה למרכז העיר?

 

א. התאימו את הגרפים המתאימים לאוטובוס ולמכונית? מי מהם נוסע מהר יותר?

ב. אילו נקודות מציינות את אמצע הדרך של האוטובוס והמונית?

ג. איזה קטע המדובר בבעיה אורכו 19.2 ? איזה קטע אורכו 12?

ד. הראו כי הביעו את שוויון היחסים במשולשים אלה.
    מה מתאר יחס הדמיון?

ה. מצאו זוג נוסף של משולשים דומים. הביעו את שוויון היחסים במשולשים אלה.

ו. השוו בין היחסים (של הסעיפים ד' ו-ה') ומצאו את המרחק בין מרכז העיר לשדה התעופה.

ז. השלימו את הגרפים עד להגעת המכונית למרכז העיר. 

    מצאו בדרך דומה כמה קילומטרים נותרו אז לאוטובוס עד ליעדו.

 

 

 

 

דרך פתרון נוספת: נסמן את הזמן של אמצע הדרך של המכונית ב-t, ונביע בעזרתו את המהירויות של המכונית והאוטובוס. נשווה בין הזמן של המכונית והאוטובוס כאשר זה הגיע למחצית הדרך.

---

במבט על - פעילות אינטרקטיבית מקסימה כמבוא לגרף המתאר תנועה.

---

פעילות הרחבה- "מרוץ מכוניות דינאמי" בו הפנייה לסימולציה של בעיית תנועה, למאמר העוסק בסגנונות למידה שונים,
ובעיות תנועה רבות בספר האלקטרוני "לראות מתמטיקה- פונקציות" של מטח.

---

 

תקציר

שתי מכוניות יצאו למסלול נסיעה באותו כיוון. נקודת ההתחלה של המכונית האדומה היא 30 ק"מ אחרי נקודת ההתחלה של המכונית הכחולה.
שתי המכוניות יוצאות למסלול באותו זמן. 
מהירות המכונית הכחולה 50 קמ"ש ומהירות האדומה 35 קמ"ש.

הכניסו את הנתונים המתאימים לסימולציה וצפו בתנועת המכוניות ע"י לחיצה על Start.
תוכלו לעצור את המכוניות בכל רגע ע"י לחיצה על Stop.
תוכלו להסיע ידנית את המכוניות בעזרת Manual Animation.

א. מהי משוואת הישר המתארת את הדרך של המכונית האדומה? של המכונית הכחולה?

ב. מתי והיכן תשיג המכונית הכחולה את האדומה?

ג. מה יהיה המרחק בין המכוניות לאחר 4 שעות?

ד. מצאו בעזרת הסימולציה:

    1. מתי יפגשו המכוניות אם המרחק ההתחלתי בין המכוניות יהיה 60 ק"מ?

    2. באיזו מהירות צריכה לנסוע המכונית האדומה בכדי שיפגשו לאחר 3 שעות? לאחר 5 שעות?

    3. באיזו מהירות צריכה לנסוע המכונית האדומה בכדי שהיא לא תיפגש כלל עם המכונית הכחולה?

בעיות תנועה דינאמיות מהספר האלקטרוני "לראות מתמטיקה- פונקציות":

• נסיעות- באמצעות הכלי נסיעות על כביש חיפה - תל-אביב אפשר לתאר נסיעות של כלי-רכב בין כמה ערים הנמצאות לאורך כביש זה.
• טיולים שונים- בפעילות יש להתאים את הגרף לסיפור הטיול המתאים.
• גרפים לתיאור תנועה - בפעילות יש להתאים לסימולציה של תנועת המכוניות את הגרף המתאים.
• משאיות - קריאת גרף וחיבור גרפים לסיפור.
• תופסת - עקבו אחר הסימולציה למשחק תופסת ובעזרת הזזות תוכלו לשנות את הפונקציות המתארות את הריצה במשחקי תופסת אחרים.
• טיול אופניים -  תיאור בעיות תנועה באמצעות גרפים והזזותיהם.
• קטנוע ואוטובוסים - בניית פונקציות וגרפים לסיפורים באמצעות כלי ההזזות.
• תוכניות לטיול - בניית פונקציות וגרפים לסיפורים באמצעות כלי ההזזות.
• נסיעות ברכב - במשימה יש להתאים ביטויים של נסיעת הרכב לחלקים שונים של הזמן.
• טיולים ושיקופים - שלושה סיפורים אחרים שאפשר לתארם בגרף על ידי הפעלת שיקופים על חלקים של הגרף הנתון, בציר אופקי ובציר אנכי.
• תיאורים שונים של טיול -  משימה עוסקת בהרכבת ביטויים המתארים את הסיפורים של מטיילים שונים. ובמציאת ביטויים שקולים לאותו סיפור.
• מהירות מופרזת - מציאת ביטויים שקולים לפונקציות המתארות תנועה.

תקציר|מערכת משוואות בשני נעלמים |פתרונות|معادلتان بمجهولين |

1. משוואות הקסם

1. בשיעורי הבית דנה התבקשה לפתור שלש מערכות של משוואות בשני נעלמים:

    דנה פתרה שתי מערכות משוואות ומצאה שפתרונן זהה והוא (x,y)=(−1,2).

    היא טענה שגם למערכת המשוואות השלישית אותו פתרון.

    האומנם? בדקו את פתרונה של דנה.

2. דנה טענה שיש למערכות המשוואות הללו מבנה מיוחד. התוכלו גם אתם לזהותו?

    תנו דוגמה למערכת משוואות דומה. מהו פתרונה?

3. דן ורונה בנו גם הם מערכת משוואות:

   פתרו את המשוואות. מה קיבלתם?

   מה מיוחד הפעם במבנה המשוואות?

4. עדי "הציצה" במחברות של דן ורונה ורשמה מערכת חדשה:

    האם 'הקסם' יעבוד גם במערכת של עדי ?

5. השלימו את המערכות הבאות כך יתקבל פתרון (x,y)=(−1,2):

6. שרטטו, במערכת צירים אחת, את ארבעת הישרים שמופיעים במערכות (1) ו-(2). בחרו מערכת משוואות 

    נוספת מבין המערכות (4) - (9) והוסיפו לשרטוט את שני הישרים הנוספים. מהי המשמעות הגיאומטרית 

    של כל הישרים הללו? 

7. מצאו תבנית כללית לרשום מערכות הקסם.     

    אתגר אלגברי -הוכיחו כי פתרון מערכת משוואות הקסם הוא (x,y)=(−1,2).

מעובד לפי "מתמטיקה בהנאה" של פרופ' אביטל.

סולמות טמפרטורה

במרבית ארצות העולם משתמשים באופן יומיומי בסולם הטמפרטורה של צלסיוס. במדינות ספורות, ביניהן ארצות הברית,משתמשים בסולם הטמפרטורה של פרנהייט. צלסיוס הגדיר את אפס מעלות כנקודת הקיפאון של המים וכ- 100 את  נקודת

הרתיחה של המים. ואילו פרנהייט הגדיר את נקודת האפס כטמפרטורה שאליה יורד קרח כתוש כאשר מערבביםאותו במלח וכ- 100 בטמפרטורה הממוצעת של חום האדם.

תיירים המבקרים בארצות בהן סולם טמפרטורה שונה מאשר בארצם , צריכים להמיר את הטמפרטורות של מזג האוויר למשל, לסולם המוכר להם. בתמונה מוצג מדחום המכויל לפי שתי השיטות ,של צלזיוס ושלפרנהייט .המדחום מאפשר המרת טמפרטורות שבין 25° ל 50° צלזיוס בלבד. הוא איננו מאפשר המרת טמפרטורות גבוהות יותר.דרך שיטתית יותר להמרת הטמפרטורה מסולם פרנהייט לסולם צלזיוס ניתנת באמצעות הנוסחה: 

(מסמנים טמפרטורה הנמדדת בסולם צלזיוס ב-C ובפרנהייט ב-Fׂ)

שאלה 1

א. איזו טמפרטורה במעלות צלזיוס מתאימה ל - 86° פרנהייט?

   בדקו האם התוצאה מתאימה לתמונה.

ב. איזו טמפרטורה במעלות פרנהייט מתאימה ל - 40° צלזיוס?

   בדקו האם התוצאה מתאימה לתמונה.

שאלה 2

לפי סולם צלזיוס , מים קופאים ב - 0° ורותחים ב- 100° בתנאי שהלחץ החיצוני הפועל עליהם הוא אטמוספרה אחת. לפי סולם פרנהייט מים קופאים ב - 32° ורותחים ב - 212°. 

א. מהו הפרש הטמפרטורה מנקודת הקיפאון לנקודת הרתיחה בסולם פרנהייט?

ב. מהו הפרש הטמפרטורה מנקודת הקיפאון לנקודה הרתיחה בסולם צלזיוס?

ג. חשבו את היחס בין שני ההפרשים שקיבלתם

   רשמו אותו כשבר פשוט, מצומצם ככל האפשר.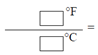

ד. מהו השינוי בטמפרטורה בסולם פרנהייט המתאים לשינוי של מעלה אחת בסולם צלזיוס?

שאלה 3

מצאו נוסחה המאפשרת המרת טמפרטורה מסולם צלזיוס לסולם פרנהייט.

שאלה 4

האם קיימת מידת חום בה הטמפרטורה שווה לפי שני סולמות המדידה?

אם כן – מהי ?אם לא – נמקו.

הפעילות לקוחה מתוך "אוריינות מתמטית" של האגף לתכנון ולפיתוח תכניות לימודים.