תקציר|אנשי החידות מהודו | פתרונות

בהודו העתיקה, בשנים 1200-200 לספירה, הייתה פריחה של יצירה עשירה במתמטיקה ובמדעים. 

הם פיתחו את נושא הגיאומטריה והטריגונומטריה לצרכי חישובים אסטרונומיים, הם פיתחו שיטות לפתרון משוואות דיופנטיות אך עיקר תרומתם הייתה יצירת המספר העשרוני, שיטת הספירה שאנו משתמשים בה עד היום. הם סימנו לראשונה את המספר "אפס" והיו גם הראשונים

לקבל את המספרים השליליים.

המתמטיקאים ההודיים הידועים ביותר הם: אריבסהטה הראשון מהמאה ה-6 שחישב בדיוק רב את המספר פאי.ברהמהגופטה מהמאה ה-7, אשר עסק במשוואות דיופנטיות והידוע בזכות משפט המשמש לחישוב שטחו של מרובע החסום במעגל לפי צלעותיו. בהסקרא השני מהמאה

ה-12 אשר עסק בפתרון משוואה ריבועית.

תרומתם של המדענים ההודים בחשבון ובאלגברה השפיעה רבות על התפתחות המתמטיקה בארצות הערב ולאחר מכן בארצות אירופה.

לפניכם כמה חידות עתיקות שהציגו המתמטיקאים ההודים העוסקות דווקא במשפט פיתגורס היווני:

1. עץ הצפצפה הבודד

על גדות נהר הגנגס צמח עץ צפצפה בודד.

לפתע הגיע משב רוח חזק וכפף את גזעו של העץ. 

נשבר העץ  המסכן וצמרתו נפלה על הגדה הנגדית של הנהר שרוחבו 4 מטרים.  גזע העץ הגאה, באורך 3 מטרים, נותר לעמוד מאונך לזרם הנהר.

התוכלו לדעת מה היה גובהו של העץ לפני שהרוח שברה אותו?

2. פרח הלוטוס הקדוש

פרח הלוטוס מקודש על הבודהיסטים, שלפי אמונתם פרץ הצמח ופרח בכל מקום עליו דרכו רגליו של הנסיך התינוק סאדהראתה (בעתיד בודהה). תחת שורשיו הנטועים עמוק בביצה שוכנים אוצרות. 

באגם שקט צמח פרח מרהיב של הלוטוס הקדוש. שורשיו של הצמח עמוק בקרקעית האגם והפרח התנשא כחצי מטר מעל פני המים. הוא היה פרח יחיד וכשרוח נשבה נישא הפרח על פני המים ונעלם רק באביב המוקדם מצא אותו דייג במרחק של שני מטרים מהמקום שבו הפרח

גדל.

התוכלו לדעת מה עומקו של האגם בו צמח הלוטוס?

3. ירושת האיכר

איכר הודי  עשיר וחובב מתמטיקה הוריש לשלושת בניו את חלקתו הריבועית.

האיכר סימן על אחת מצלעות המגרש את אמצעו (E) ומתח קו עד לנקודה כלשהי על הצלע שממול (F). 

הבן הצעיר קיבל חלקה בתוך המגרש בצורת משולש אשר שטחו 9 דונם.

את שתי החלקות הנותרות הוריש לשני בניו הבכורים התאומים.

מהי הנקודה (F) שבחר האיכר כך ששטחי חלקות הבנים התאומים היו שווים?

4. המנזר הבודהיסטי

כל יום יצא האיכר ההודי מביתו (A) לתפילת הבקר במנזר ((B.

הוא הלך בקצב מתון ומדוד בעודו ממלמל את אותה שירה בכל יום ויום.

לעיתים היה עושה את דרכו דרך המעיין הקדוש (C) ולעיתים עבר דרך הנהר (D). 

התוכלו להביע את הדרך מבית האיכר לנהר (AD=d) לפי הדרך מבית האיכר למעיין (AC=a)

ומן המעיין עד המנזר (CB=b)?

מהי התשובה הנכונה?

הפיצוח נכתב ע"י נטליה קונצ'יקוב במסגרת קורס כתיבה יצירתית במתמטיקה

תקציר|יצירת מגן דוד|

בעזרת סרגל ומחוגה תוכלו ליצור עיצובים מרהיבים של מגן דוד, באופן הבא:

1) שרטטו מעגל בעזרת מחוגה. 

    שימרו על מרחק בין שתי רגלי המחוגה עד לשלב הבא.

2) סמנו נקודה. על המעגל , העמידו את חוד המחוגה על הנקודה שסימנתם וסמנו נקודה נוספת על המעגל.

   חזרו על פעולה זו  מספר פעמים עד שתקבלו שש נקודות על הקף המעגל.

   מדוע יש בדיוק שש נקודות? 

3) חברו כל נקודה עם שתי נקודות שנמצאות ממולה (החיבור נעשה לסירוגין בין הנקודות שסימנתם על הקף המעגל). 

    קיבלתם מגן דוד, שמו המתמטי הקסגרם.

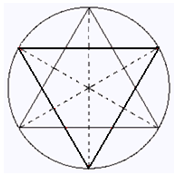
4) שרטטו בעזרת סרגל שלושה קטרים מקווקווים. (בהמשך תמחקו אותם)

5) ציירו שני משולשים שקודקודם בנקודות המפגש הקטרים עם צלעות המשולשים הגדולים.

    קיבלתם מגן דוד פנימי קטן.

6) כעת תוכלו להדגיש את הקווים שברצונכם בכדי ליצור את המגן דוד המעוצב.

    לפניכם שלש צורות שיוכלו להיות בסיס ליצירתכם.

    צבעו את חלקי המגן דוד כרצונכם.

    התוכלו למצוא עיצובים נוספים למגן הדוד?

על בסיס אותו רעיון תוכלו לצייר מגו דוד בתוך מגן דוד בתוך מגן דוד...עוד ועוד.

מקור:  http://www.mathcats.com/crafts/hexagrams.html

קישורים נוספים לחקר צורת מגן הדוד והצעות לפעילות:

"מגן דוד", במונחים מתמטיים ידוע כהקסגרמה, הוא המוטיב המרכזי בדגל ישראל ולו תכונות מתמטיות מרתקות. 

בקישורים הבאים תוכלו להעמיק וללמוד על תכונותיו המעניינות, על מקורותיו וההסטוריה המגוונת שלו בתרבויות השונות, והמשמעויות השונות שהעניקו לו. תוכלו גם להתרשם מאוסף עשיר של יצירות מגני דוד בציורי קיר, איורים, תחריטים, פסיפסים ופסלים.

מגן דוד - מידע תמציתי בויקיפדיה.

גיאומטריה של מגן-דוד - בעיית החודש מס' 5 - קשר חם.

חומשי - עיתון לעידוד המתמטיקה פרי עטו של ג'רי רוזן ז"ל המוקדש כולו למגן דוד. שם תמצאו מידע ופעילויות, חידות , הצעות ליצירה, קיפולי נייר ועוד.

אלבום מגן דוד - בלוג עשיר מאין כמוהו של זאב ברקן ובו מידע על מקורו, עברו, המשמעויות השונות שמיוחסות לצורתו של המגן דוד בתרבויות השונות. באתר אוסף עצום של תמונות ויצירות של מגני דוד.

מצגת מגן דוד והדגל - בעריכת אסף פלר.

יצירות ואיורים של מגני דוד בהשראת מתמטיקה מתחרות שנת השישים מטעם מרכז המורים במתמטיקה.

רימון, מגן דוד ומתמטיקה - מצגת שנוצרה בביה"ס "אורט במעלה" טבריה, במסגרת תחרות "תמונה ישראלית בעין מתמטית"

תקציר| פחות או יותר| פתרונות

 1.  האוצר

חבורת "כח המח" מצאה בשיטוטיה, שק ובו אוצר של מטבעות זהב וכסף. הם העריכו שמשקלו לא יותר מ-1 ק"ג. כל מטבע זהב שוקל כ-10 גרם וכל מטבע כסף שוקל כ-5 גרם.
כמה מטבעות מכל סוג ייתכנו בשק?

א. סמנו את מספר מטבעות הכסף ב- x ואת מספר מטבעות הזהב ב- y.
    הביעו באמצעות x ו- y את משקל המטבעות בשק.

ב. אילו מהביטויים הבאים מתארים את הערכת המשקל של שק המטבעות.

ג. לפניכם גרף המתאר את משקל שק המטבעות.

1.  כמה מטבעות בשק אם היו רק מטבעות זהב? רק מטבעות כסף?
     סמנו נקודות אילו בגרף.

2. מה מספר מטבעות הזהב ומטבעות הכסף האפשריים כך שמשקל השק הוא בדיוק 1 ק"ג.
    סמנו נקודות אילו בגרף. מה מאפיין אותן?

3. תנו כמה דוגמאות לתכולת שק שמשקלו יותר מ-1 ק"ג.
    סמנו נקודות אילו בגרף. היכן נמצאות הנקודות ביחס לישר?

4. תנו כמה דוגמאות לתכולת שק שמשקלו פחות מ-1 ק"ג.
    סמנו נקודות אילו בגרף. היכן נמצאות הנקודות ביחס לישר?

שרטוט גרף לאי שוויון לינארי

1. שרטטו ישר המתאים לשוויון. השתמשו בקו רציף כאשר אי השוויון הוא של קטן/גדול ושווה,
    ובקו מרוסק כאשר אי השוויון הוא קטן/גדול ממש.

2. הישר ששרטטתם מחלק את המישור לשני חצאים. 
    בחרו נקודת מבחן כלשהי באחד החצאים ובדקו האם היא מקיימת את אי השוויון.

3. אם נקודת המבחן מקיימת את אי השוויון הצלילו את כל חצי המישור בו היא נמצאת. 
    אם לא הצלילו את חצי המישור השני.

2.  במגרש הכדורסל 

נותרו עוד שתי דקות לשריקת הסיום במשחק הכדורסל.
קבוצתכם בפיגור של 12 נקודות. 
באפשרותכם לקלוע זריקות של 3 נקודות ושל 2 נקודות בלבד. 

מהן האפשרויות שלכם לזריקות לסל כדי לזכות בלפחות 12 נקודות ?

א. סמנו את מספר הקליעות של 2 נקודות ב- x ואת מספר הקליעות של 3 נקודות ב- y. הביעו באמצעות x ו- y את מספר הנקודות האפשרי ורשמו את אי השוויון המתאים.

ב. שרטטו במערכת הצירים גרף לאי השוויון. סמנו בגרף נקודות העונות על תנאי השאלה. זכרו מספר הקליעות הוא מספר שאינו שלילי ושלם.

3.  ארוחת בוקר בריאה 

עליכם לתכנן תפריט לארוחת בקר בריאה שתכיל לכל היותר 500 קלוריות, ע"פ הטבלה הבאה:

א. בחרתם כוס מיץ עגבניות, דגנים וחלב. איזו כמות של דגנים וחלב תוכלו לכל היותר לקחת?

ב. בקר אחר בחרתם לאכול לחמנייה. איזו כמות של גבינה לבנה וכוסות מיץ תפוחים תוכלו לאכול?

ג. אם תרצו לאכול לחמנייה וביצה, כמה כוסות מיץ (תפוחים ועגבניות) תוכלו להוסיף?

ד. תכננו לכם ארוחת בקר נוספת.

יישומים אינטראקטיביים לשרטוט גרף לאי שוויון לינארי:

פתרון אי שוויון או מערכת אי שוויונות לינארית - ישום בעזרת Geogebra. (נדרש תוסף ג'אווה בדפדפן שאינו כרום)

פתרון מערכת אי שוויונות לינאריים באמצעות גרפים - יישום מבית 

פעילויות ומאמרים בנושא אי שוויונות לינאריים:

משוואות של אי-שוויונים ממעלה ראשונה במישור - מחר 98- התרת מערכות "או" ומערכות "וגם" של אי-שוויונים ממעלה ראשונה בשני משתנים, תוך התייחסות לצורת תחום הפתרון. זוהי הקדמה לחוברת "תכנון לינארי - מושגים, שיטות, יישומים - לימוד בשילוב מחשב".

לביצוע המטלות ניתן להעזר בכל תוכנת מחשב המאפשרת חקירת פונקציות ו/או במחשבון גרפי.

התרת אי-שוויון ומערכת אי-שוויונים ממעלה ראשונה- מחר 98- דפי עבודה לתלמיד בנושא: הפונקציה הקווית, המשלבים את המחשב בלימוד הנושא. דפים אלה הם חלק מחוברת הנקראת "שילוב המחשב בלימוד המתמטיקה - הפונקציה הקווית. הדפים בנויים בצורה של גילוי של תכונות הפונקציה, ע"י העלאת השערות ובדיקתן של דוגמאות רבות במחשב. בנוסף לכל דף עבודה לתלמיד, יש דף למורה המכיל המלצות למורה וכן הפניה לנספח.