תקציר|אני ואתה נשנה את העולם |פתרונות|أنا وأنت نغيّر العالم

זוכרים את הסרט "תעביר את זה הלאה" ("Pay It Forward")?  זוהי דרמה המבוססת על הספר המצליח של קתרין ריאן הייד. הסרט יצא בשנת 2000 וגרם לאנשים רבים שצפו בו לפעול ברוח הרעיון, לתרום לחברה ולהאמין כי "אני ואתה נשנה את העולם".

טרוור הוא ילד ממשפחה קשת יום שחי בלאס וגאס. כאשר הוא מגיע לכיתה ז' בבית הספר הוא מקבל מהמורה שלו משימה לימודית - לנסות ולמצוא דרך שתשנה את העולם.

צפו בסרט אחר הרעיון הקטן של טרוור שיכול לעשות שנוי גדול:

"אני אעשה משהו טוב עבור שלושה אנשים. וכשהם ישאלו כיצד הם יגמלו לי בעבור זה, אני אומר להם תעבירו את זה הלאה... כל אחד מכם יעביר לעוד שלושה אנשים. כך יוצא שתשעה אנשים נוספים יצטרכו לעשות מעשה טוב לעוד עשרים ושבעה! ואז תנסו לחשב... אתם רואים כמה גדול זה יוצא?"

נניח כי בכל יום "מעבירים את זה הלאה".

1. מה תוכלו לומר על הגידול של מספר האנשים שמעבירים את זה הלאה ככל שהימים חולפים?  
    התוכלו לנחש כמה אנשים יעבירו מעשה טוב ביום ה-6 ? 

    התוכלו לנחש באיזה יום יותר מ-1000 אנשים נוספים יעבירו מעשה טוב הלאה? 

    כעת נחשב "כמה גדול זה יוצא?" - השלימו את הטבלה את הדינאמית (אקסל), וסמנו נקודות מתאימות במערכת הצירים.

 הערה- תוכלו להיעזר במילוי הטבלה בגיליון האלקטרוני בנוסחה והעתקתה. (בכל שלב גדול מספר האנשים שקיבלו להעביר הלאה פי שלוש מהשלב הקודם) 

2. המבצע שיזם טרוור "להעביר את זה הלאה" עבד שישה ימים.

    כמה אנשים נוספים עשו מעשה טוב ביום השישי? 

    מה מספר המעשים הטובים שנעשו במבצע "העבירו הלאה" במהלך ששת הימים?

3. המבצע "להעביר את זה הלאה" עבד n ימים.

    כמה אנשים נוספים עשו מעשה טוב ביום ה-n?

    מה מספר המעשים הטובים שנעשו במבצע "העבירו הלאה" במהלך n הימים?

4. באיזה יום מתחילת המבצע כל תלמידי הכיתה שלכם "יעבירו את זה הלאה" לאחרים?

     כמה ימים דרושים כדי שכל תלמידי בית הספר שלכם "יעבירו את זה הלאה" לאחרים?

     האם ניתן להעריך זאת מתוך הנקודות שסימנתם במערכת הצירים?

5. התבוננו במערכת הצירים בגרף שיצרתם. האם כדאי לחבר את הנקודות שעל הגרף?

    האם תוכלו למצוא נקודה בה x=6.5 ? מה המשמעות של נקודה זו?

    כיצד לדעתכם נראה הגרף של מבצע "העבר את זה הלאה"?

6. חשבו כמה זמן ייקח עד ש-1000 אנשים בדיוק יעבירו הלאה מעשה טוב לאחרים.

7. כיום יש במדינת ישראל כ- 7,500,000‏‏‏ תושבים. 

    כמה ימים דרושים כדי שכל תושבי מדינת ישראל ייטלו חלק במבצע?

8. כיצד היה משתנה אופן גידול האנשים אם טרוור היה מציע "להעביר הלאה" בכל יום לאיש נוסף אחד בלבד? 

    כיצד הייתה משתנים הגרף והחוקיות?

9. כיצד תשתנה החוקיות אם מעבירים הלאה בכל יום לשני אנשים נוספים? 

    לשלושה, לארבעה אנשים נוספים?

    התאימו גרף לכל מקרה.

10. לקראת פורים, בית הספר "חופים", בו 1000 תלמידים, פתח במבצע של משלוחי מנות. 

        על כל תלמיד לשלוח לשלושה אנשים משלוח מנות. וכל אחד מהם עליו לשלוח משלוח מנות לשלושה אנשים נוספים.

        תוך כמה צעדים במבצע יקבלו יותר ממיליון אנשים משלוח מנות?

        כיצד תשתנה החוקיות? כיצד ישתנה הגרף?

פרוייקט "תעביר את זה הלאה" בשפת הסימנים

זהו פרוייקט חברתי-התנדבותי ליצירת מודעות, גישור ואיחוד בין הקהילה ה'שומעת' והקהילה ה'חירשת' בישראל. למד את שפת הסימנים והעבר את הידע שלך הלאה, כך נרחיב את קהילת דוברי שפת הסימנים.

"תעביר את זה הלאה" - פרוייקטים קהילתיים

המקום בו נפגשים אנשים טובים כדי לעשות מעשים טובים.

פינג-פונג מתמטי - על"ה 38, תשס"ז 2007, רון אהרוני, גילוי נוסחא לסכום של סדרה גיאומטרית.

תקציר|אני דומה לעצמי?|أنا اشبه نفسي

הכירו את הפקרטל המפורסם, משולש סרפינסקי.

משולש סרפינסקי נוצר בסדרה אינסופית של משולשים

הדומים לעצמם בכל רמת פירוט שנסתכל בה.

לתכונה זו קוראים,  "דמיון עצמי" ,כלומר כל חלק של הפרקטל נראה כמו השלם, החלק של החלק נראה כמו החלק וכך הלאה....

1. עקבו אחר התפתחות הפרקטל של משולש סרפינסקי, ביישומון הפרקטל  או בתמונה למטה:

א. תארו כיצד בכל שלב תמונת המשולש משתנה. 

    מה משתנה במעבר משלב לשלב, ומה נשאר קבוע?

ב. מצאו חוקיות בסדרה ותארו אותה.

ג. התבוננו בשלב השני ומצאו זוגות של משולשים דומים (שאינם זהים)? מהו יחס הדמיון בכל זוג?

    אילו משולשים דומים ניתן למצוא בשלב השלישי? מהו יחס הדמיון בכל זוג?

    תארו את בניית משולש סרפינסקי בעזרת משולשים דומים.

ד. כמה משולשים ירוקים בשלב השלישי? כמה יהיו בשלב הרביעי? כמה יהיו בשלב ה- n?

ה. כמה משולשים לבנים בשלב השלישי? כמה יהיו בשלב הרביעי? כמה יהיו בשלב ה- n?

ו. נניח בשלב התחילי שטח המשולש הירוק הוא 1 יחידה רבועה.

   מהו שטח המשולשים הירוקים בשלב הראשון? השני? השלישי? 

   התוכלו להעריך את שטח המשולשים הירוקים בשלב ה-100? בשלב ה- n?

2. ניתן לעצב פרקטלים מרהיבים בצורות שונות שלהם תכונת הדמיון העצמי. 

האם תוכלו לבנות סדרה בחוקיות דומה בריבועים? נסו לציירה ולמצוא את יחס הדמיון בה.

אם תתבוננו מסביבכם תמצאו פרקטלים רבים בטבע:

עצים וענפים, הכרובית והברוקולי, פתית השלג, צדפים, הברקים וסופות הוריקן ועוד.

מנדלברוט (1924-2010), מתמטיקאי יהודי, היה  הוגה רעיון הפרקטלים. הראה, שתכונת הדמיון העצמי איננה גחמה מתמטית של גיאומטריה. היכולת להמשיך סדרות כאלו עד אין סוף התגלתה הודות ליכולתם של מחשבים מודרניים לבצע מיליארדי פעולות בשנייה, אבל היא קיימת בטבע, באוויר, בים וביבשה.

Where do we find fractals? - פוסטר מאת Fractal Foundation

3. לפניכם פרקטל ריבועי נוסף מתוך יישומון הפרקטל :

א. תארו כיצד בכל שלב תמונת הריבוע משתנה.

    מה משתנה במעבר משלב לשלב, ומה נשאר קבוע?

ב. מצאו חוקיות בסדרה ותארו אותה.

ג. התבוננו בשלב השני ומצאו זוגות של רבועים דומים (שאינם זהים)? מהו יחס הדמיון בכל זוג?

    אילו מרובעים דומים ניתן למצוא בשלב השלישי? מהו יחס הדמיון בכל זוג?

ד. כמה ריבועים מכל צבע בשלב השני? השלישי? כמה יהיו בשלב הרביעי? כמה יהיו בשלב ה- n?

ה. נניח בשלב התחילי (שלב אפס) הוא 1 יחידה רבועה.

    מהו שטח הריבוע הכתום בשלב הראשון? בשלב השני? השלישי? בשלב ה- n?

ו. נניח בשלב התחילי שטח הריבוע הכתום הוא 1 יחידה רבועה.

   מהו שטח הריבועים הכחולים בשלב הראשון? השני? השלישי? בשלב ה- n?

קראו עוד על פרקטלים:

לחיות עם אי הודאות - צבי ינאי, מדור מדע ב-YNET.

פרקטלים ומשולש סרפינסקי וחקר השברים (עמ' 4-6) - מרכז ארצי למורים למתמטיקה בחינוך היסודי

משחקים כסביבה להצגת מושגים ומשפטים מתמטיים ולפתרון בעיות, חלק ב' - נצה מובשוביץ הדר, על"ה 41.

תוכלו לקרוא על המימדים של פרקטל- מאמר מאת NRICH

Ron Eglash on African fractals | Video on TED.com - הרצאת וידאו (אנגלית עם תרגום לעברית) - מומלץ

תקציר| זהו את הזהות הטריגונומטרית| פתרונות| ميّزوا المتطابقات المثلثية| حلول

1. זהויות טריגונומטריות לסכום זוויות

באיור הבא נתון DB=1.

א. איזה קטע באיור שווה ל- (sin(α+β ?   

    איזה קטע באיור שווה ל- (cos(α+β ? 

ב. שנו באיור הדינאמי את הזווית α באמצעות הקודקוד A,     

    כך שסכום הזוויות α+β  נשאר קבוע.   

    אילו גדלים משתנים באיור ואילו נשמרים? 

    האם מתקיים sin(α+β)=sinα+sinβ ?

    האם מתקיים cos(α+β)=cosα+cosβ ?

ג. שנו באיור הדינאמי את הזווית β באמצעות הקודקוד B,   

    כך שסכום הזוויות α+β למעשה משתנה.

    אילו גדלים משתנים באיור ואילו נשמרים? 

    האם מתקיים sin(α+β)=sinα+sinβ ?

    האם מתקיים cos(α+β)=cosα+cosβ ?

*  אילו זוויות α, β מקיימות sin(α+β)=sinα+sinβ ?

   ברצוננו להביע את (sin(α+β באמצעות sinα ו- sinβ בלבד. 

ד. הביעו את אורכי הקטעים:

GH, BF, HF, DG, DH, BH באמצעות β,α בלבד.      

ה. רשמו נוסחאות מתאימות:

_________________ = (sin(α+β

_________________ = (cos(α+β

ו. רשמו נוסחאות מתאימות לזווית כפולה:

_________________ = (sin(2α

_________________ = (cos(2β

מקור: הוכחות ויזואליות: השקפותיהם ואמונותיהם של התלמידים, רז הראל טומי דרייפוס, על"ה 41

2. זהויות טריגונומטריות לזווית כפולה

א. הסבירו מדוע זווית AOB> כפולה מזווית BAM>  

ב. עקבו באיור הדינאמי אחר השתנות הזוויות וערכי הסינוס שלהן. 

ג. הביעו את AM בשתי דרכים:

    1) בעזרת משולש ΔAOM  

    2) בעזרת משולש ΔABM 

    מה ניתן להסיק?  

ג. כיצד תוכיחו את הנוסחה כאשר הזווית AOB> קהה?

ד. הביעו את OM בשתי דרכים. מה תוכלו להסיק הפעם? 

מקור: NRICH

3. עוד זהויות טריגונומטריות לזווית כפולה 

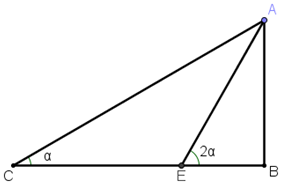
באיור הבא נתון CB=2.

נסמן t=tanα.

הביעו את אורכי צלעות המשולשים באיור באמצעות t.

הוכיחו באמצעות האיור את הזהויות הטריגונומטריות הבאות לזווית כפולה:

4. זהויות טריגונומטריות מפתיעות 

ידועה הנוסחה: 

נסמן tanα=t. הוכיחו את הזהויות ושימו לב לתופעה המפתיעה:

מה נקבל אם נרשום ממול כל אחד מהזהויות את המקדמים של t מהמונה ומהמכנה בסדר עולה?

מהי הנוסחה ל- (tan(5α?  ל- (tan(nα?

זהויות טריגונומטריות בשילוב גישת "מה אם לא?" - גילה רון, אורית זסלבסקי, קשר חם.

משחקים ודפי עבודה לתרגול בטריגונומטריה - NCTM