ג. האם גם אויילר שיחק בכדורגל?

תקציר |  האם הכדורגל הוא עגול?  |  בערבית

אוילר, מתמטיקאי ידוע מהמאה ה-18, חקר את הפאונים ותכונותיהם, בבעיות שעסקו בהן כבר היוונים הקדמונים, וגילה תובנה שחמקה מעיני המתמטיקה במשך אלפיים שנים לערך, נוסחת אוילר. הוא גילה קשר מספרי בין מספר מספר הפאות (F), מספר הקודקודים (V) ומספר המקצועות (E).

אולי כבר גיליתם בעצמכם?       

קראו עוד על הגופים האפלטוניים, נוסחת אוילר לפאונים, וכדורגל בבלוג "לא מדויק".

נשאלת השאלה האם הכדורגל וגופים אחרים גם הם מקיימים את נוסחת אוילר? בדקו בעצמכם את הנוסחה עבור הכדורגל, העשרימון הקטום, וצפו בסרטון.

קראו עוד על נוסחת אויילר (באנגלית).

מקורות נוספים:
אוילר וגאוס ביצירתם ובחייהם - אלה שמוקלר, קשר ח"ם
הגופים האפלטוניים, נוסחת אוילר לפאונים, וכדורגל - רשומה מאת גדי אלכסנדרוביץ' בבלוג "לא מדויק"

 המשך לחלק ד' - כדורגל בחלל

ב. מהם גופים חצי משוכללים? ואיזה גוף הוא הכדורגל?

תקציר |  האם הכדורגל הוא עגול? |  בערבית

תרגיל בדמיון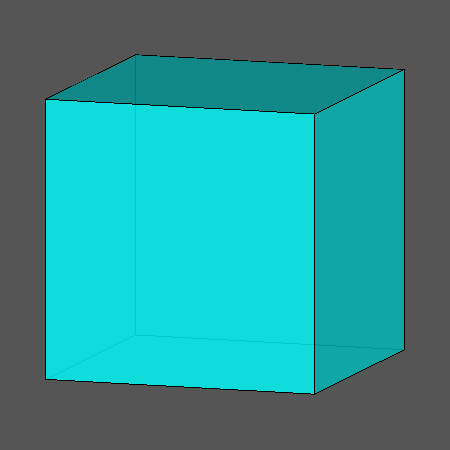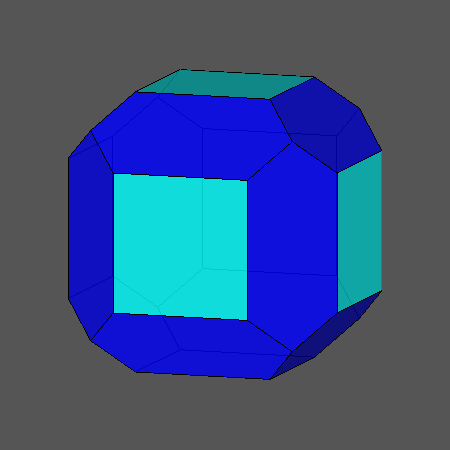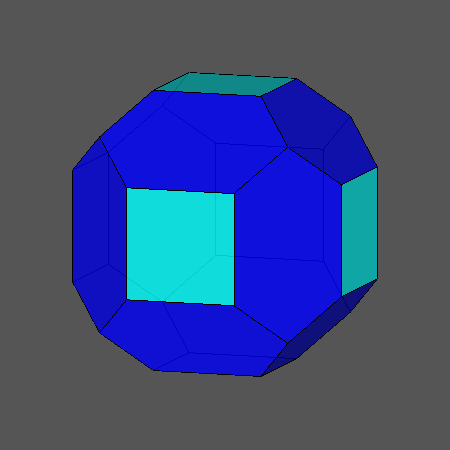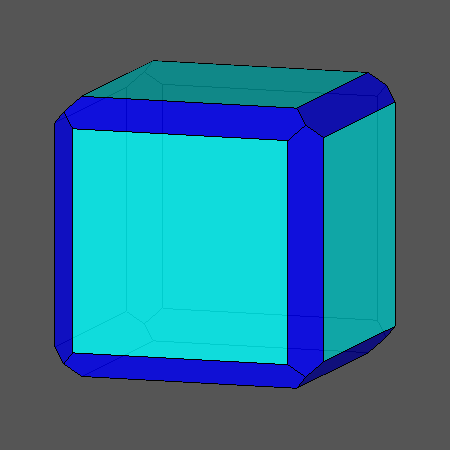 

בפניכם קובייה. כעת נסו לדמיין שקוטמים כל פינה בקובייה, איזה גוף נקבל? אילו מצולעים תקבלו בכל פינה?
כמה מצולעים כאלה יהיו בגוף החדש? האם בגוף הקטום יהיו גם מצולעים אחרים כמה? ראו אנימציה.

ראו גם פיצוח "לחתוך את הקוביה" בו תוכלו להתנסות בעזרת יישומון בחיתוך הקובייה.
גוף חצי משוכלל הוא גוף שכל פאותיו מצולעים משוכללים (מסוגים שונים), ומכל אחד מקדקודיו יוצא אותו מספר מקצועות (צלעות).

ארכימדס חקר את הגופים הקטומים של הגופים המשוכללים, וקיבל אוסף חדש של 12 גופים חצי משוכללים, הידועים בשם פאונים ארכימדים. המפורסם שבהם הוא העשרימון הקטום, הוא הכדורגל. קראו מאמר באלף אפס בנושא, אל תקלקל לי את המעגל, מאת זיוה דויטש ועקיבא קדרי.

ראו סרטון מאת NuberPhile על העשרימון הקטום, הוא הוא הכדורגל! שימו לב כמה פיאות לכדורגל ומהן תכונותיהן?

בנו לעצמכם כדורגל מנייר.

מקורות נוספים:

הסברים ואנימציות על גופים חצי משוכללים (באנגלית)

 המשך לחלק ג' - האם גם אויילר שיחק בכדורגל?

בדרך לפיתגורס- ריבועים רוקדים

תקציר| בדרך לפיתגורס| פתרונות| الطريق الى فيتاغوروس| حلول

א. המשחק "השלימו לריבוע"

בואו נשחק משחק. ברשותכם רשת נקודות. 
כל שחקן בתורו בוחר נקודה על הרשת ומסמנה בצבע משלו. 
השחקן המנצח יהיה הראשון אשר יהיו לו ארבע נקודות שניתן לחברן לריבוע. 
ריבוע יכול להיות מסובב ומכל גודל.

ניתן לשחק במשחק האינטראקטיבי מול המחשב או מול חבר, או בעפרון ונייר על דף הרשת הבא.

ב. לפניכם כמה ריבועים מתוך המשחק. 
המרחק בין כל שתי נקודות יחידה.

התוכלו לחשב את אורך הצלע של כל ריבוע ?שטחו של כל ריבוע?

ודאי שמתם לב שיש ריבועים שמיד ניתן לראות את אורך הצלע שלהם ומכאן בקלות לחשב את שטחם.  כיצד תאפיינו ריבועים אלו ואת הקשר בין אורך צלע הריבוע ושטחו?

אך, לא קל למצוא באופן מיידי את אורך הצלע של הריבועים "המסובבים". האם מצאתם? הכיצד?
הנחיה- מצאו את השטח של  הריבוע המסובב בעזרת ריבוע נוסף החוסם אותו וארבעת המשולשים המקיפים אותו.

ג. בחקירה הבאה תוכלו להיעזר ביישום דינאמי בו ניתן לסובב ריבוע בעזרת החיצים.

(1). נתבונן בסדרת ריבועים מסובבים שהוטו יחידה אחת מעלה.

חשבו את שטחי הריבועים בסדרה. האם מצאתם חוקיות בין שטחי הריבועים הללו?
התוכלו לדעת מה יהיה שטח הריבוע הבא בסדרה?

(2). בדקו האם קיימת חוקיות לשטח של סדרת ריבועים שהוטו 2 יחידות מעלה. 
      3 יחידות ? 4 יחידות? n יחידות?

                                                  ריבוע הנטוי 4 יחידות          ריבוע הנטוי 3 יחידות             ריבוע הנטוי 2 יחידות

הפעילות פותחה לפי nrich (ניתן לצפות גם בסרטונים להדגמת השיעור)

מקורות נוספים להעמקה והרחבה:

• מאדריכלות נוף למשפט פיתגורס- הצעות לפעילות של מטח
• Pythagorean Theorem- IES - אוסף יישומים דינאמיים של הוכחות למשפט פיתגורס ושימושים בבעיות שונות. 
• כתבה וערכה - נאווה מזרחי חט"ב "מיכה רייסר"- ראשון לציון
•  הרפתקה פיתגוראית- מאמר מבית "אלף אפס" המספר את סיפור מסע היתדות בן ה-3700 שנים על שלשת המספרים הידועה כשלשת פיתגורס. כתבו: זיוה דויטש, עקיבא קדרי
•  משפט פיתגורס- מבחר הוכחות ללא מילים, מאמר של "אלף אפס" ועוד חידות בנושא ויישומו.
•  "כל דבר הוא מספר"- מאמר מאת "בארץ הדעת", על תפיסותיו של פיתגורס את מושג המספר ואת המספרים הרציונאליים. כתב: רועי יהושע.
• מצגת על הוכחות של משפט פיתגורס, שלשות פיתגוריות ועוד - פסגה הרצליה, מרים עוזר, רונית רביע, ריטה שכטר
• נגריה מתמטית - בעיית החדש, קשר חם - מוצגת בעיה העוסקת בבניית ריבוע ששטחו שווה לשטח מלבן נתון. הבניהמתבססת על משפט פיתגורס, ומובילה להוכחתו בדרך גיאומטרית. מצורף פתרון לבעיה.

עוד פיצוחים:

• אוצרות פיתגורס - בפעילות חידות לחישוב שטחים הדורשות יישום של משפט פיתגורס וידע על המעגל.
• משימה פרחונית - במשימה מוצגות צורות גאומטריות בעיצוב של פרחים ויש לחשב את שטחן.
• ללכת על פני הקוביה והתיבה - יישום משפט פיתגורס במרחב
• אנשי החידות מהודו - בפעילות כמה בעיות עתיקות מהודו העוסקות במשפט פיתגורס.

playing math with your food By George Hart  for the museam of mathematics