א. הגופים המשוכללים

תקציר | האם הכדורגל הוא עגול?|  בערבית

ראשית נכיר את חמשת הגופים המשוכללים, הידועים כגופים האפלטונים:

מתוך ויקיפדיה

מה מייחד את הגופים המשוכללים?

1. כל הפאות בגוף חופפות.
2. בכל קודקוד נפגשים אותו מספר של פאות.

צפו בסרטון חמשת הגופים המשוכללים מאת numberphile.
הכירו את הגופים ושאלו את עצמכם מדוע קיימים אך ורק חמישה גופים משוכללים?

בפעילות האינטראקטיבית הבאה תוכלו לצפות באנימציה תלת מרחבית של חמשת הגופים ולסובב אותם בעצמכם. ניתן גם לסמן את הפאות ולספור אותן (F-faces), את הקודקודים (V-vertices) ואת המקצועות (E-Edges).
באפשרותכם גם להדפיס את הפריסות ולבנות את הגופים.

השלימו את הטבלה האינטראקטיבית ובדקו תשובותכם.

מצאו קשרים אפשריים בין מספר הפאות (F) , מספר הקודקודים (V) ומספר המקצועות (E).

מקורות נוספים:
בנה בעצמך גופים משוכללים (בעזרת קיפול וללא דבק), שמואל אביטל, קשר חם.
למה קיימים רק 5 פאונים משוכללים? כיתהפיתה
אוילר וגאוס ביצירתם ובחייהם - אלה שמוקלר, קשר ח"ם

 המשך לחלק ב' - מהם גופים חצי משוכללים? ואיזה גוף הוא הכדורגל?

עד קצה הגבול

תקציר| עד קצה הגבול| إلى أقصى الحدود

ארבעה חברים חובבי מתמטיקה כינו זה את זה בשמות מתמטיקאים מפורסמים. 
הארבעה התערבו מי יצליח לחשוב על פונקציה, בה מעורב המספר 100 ואשר תתן ערך גדול יותר עבור מספרים גדולים.
הראשון, המכונה נפייר, בחר פונקציה לוגריתמית:
 
השני, המכונה ברנולי, בפונקציה מעריכית:  

השלישי, ארכימדס, החליט לבחור בחזקות של  100:

הרביעי, המכונה דה-מואבר, אוהב להיות מיוחד , בחר בפונקציה שהיא מכפלה:    

א. מי מהחברים לדעתכם בחר בפונקציה המקבלת ערכים גדולים יותר עבור ערכי x גדולים?
ב. התוכלו למצוא מאיזה ערך של x הפונקציה הזו אכן גדולה יותר?
ג. כיצד ישתנו הפונקציות אם נחליף את המספר 100 במיליון? ביליון?

אשר- מתוך האתר הרשמי

 לפניכם זוג של פונקציות:

   
((g(x) פונקציה מורכבת. 

א. התאימו לכל פונקציה את הגרף.
ב. במה דומות ובמה שונות הפונקציות הללו?
    היעזרו ביישום הדינאמי (גיאוגברה) ועקבו אחר נקודות שונות.
    התייחסו בתשובתכם לנקודות בעלות מאפיינים ייחודיים כמו נקודת קיצון, ונקודות פיתול. 
    תחומי עליה וירידה ולאסימפטוטות. נמקו.

ג. נתונה הפעם הפונקציה:

   שערו כיצד נראה גרף הפונקציה-

   תוכלו להיעזר ביישום הדינאמי (גאוגברה) ורשמו בשורת הקלט למטה:

   האם הקשרים ששיערתם בסעיפים הקודמים מתקיימים גם לגבי הזוג החדש? נמקו.
   בדקו את השערתכם עבור פונקציות שונות.

ד. מצאו פונקציות נוספות שהרכבתן שומרת על התכונות שמצאתם.
ה. מצאו את הגבול של הביטויכאשר וכאשר .
    הנחיה - מצאו זוג פונקציות בדומה לסעיפים הקודמים , חקרו ושרטטו סקיצה לגרפים.

א. התבוננו בגרפים של הפונקציה המעריכית והלוגריתמית. עקבו אחר הערכים והשלימו:
    ניתן לעקוב אחר הערכים ביישום הדינאמי.

ב. השלימו על פי הגבולות שמצאתם לעיל:  

חקרו את הפונקציות הבאות לפי:
1. תחום הגדרה והתנהגות הפונקציה סביב נקודות אי ההגדרה.
2. נקודות חיתוך עם הצירים
3. התנהגות הפונקציה כאשר  וכאשר 

והתאימו להן את הגרפים:

הפעילות נערכה על פי הרעיון במאמר : יישום גבולות לשרטוט גרפים - אלה שמוקלר, מחר 98

מקורות נוספים להעמקה והרחבה:

הפוך על הפוך - פיצוח בנושא פונקציות הפוכות

גישה אינטואיטיבית לבניית מושג הגבול - תמר זמיר ונצה מובשוביץ- הדר, קשר ח"ם.

יישום גבולות לשרטוט גרפים - אלה שמוקלר, מחר 98

זוגות של פונקציות - מחר 98

אסימפטוטות המקבילות לציר ה-x  -  יפים כץ, על"ה 31

חדו"את היצירה - עופר ליבה- על"ה 23, על"ה 24

מספרים גדולים בעולם- פעילות של מרכז המורים למתמטיקה בחינוך היסודי

האינסוף המיסתורי - פרוייקט לתלמידים - מחר 98

אינסוף- הסיפור שאינו נגמר, סקירה על ספרו של פרופ' חיים שפירא, על"ה  15

האפס- ביוגרפיה של רעיון מסוכן - צ'רלס זייף - המלצה על הספר

הצעה להוכחת המשפט: גבול של שורש n י של n כאשר n שואף לאינסוף הוא 1 - עלי עותמאן, על"ה 36

ביליארד מתמטי

תקציר | ביליארד מתמטי | פתרונות | בערבית

תמר והדר המציאו משחק חדש בהשראת שולחן הביליארד.
כללי המשחק: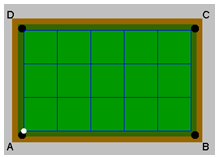 

• המשחק נערך על שולחן מלבני מנייר משובץ.
  ארבע הפינות מסומנות ב- A, B, C, D.
• הכדור הדמיוני יוצא מקודקוד A, ונזרק בזווית של 45^o.
  אם הכדור פוגע בדפנות השולחן הוא ממשיך במסלולו שוב בזווית של 45^o לדופן השולחן.
• הכדור נעצר כאשר הוא מגיע לאחת מפינות השולחן.
• ניתן לשנות את מימדי השולחן.
  
  

1. צפו במשחקון בשולחן 3X5. 
א. באיזו פינה עצר הכדור?
ב. בכמה פגיעות בשולחן הגיע למטרתו?
    (כולל הפגיעות של ההתחלה ושל הסיום).

תוכלו להתנסות במשחק האינטראקטיבי (נדרש תוסף ג'אווה בדפדפן שאינו כרום),  או בעזרת עפרון ונייר, בשולחנות הבאים:

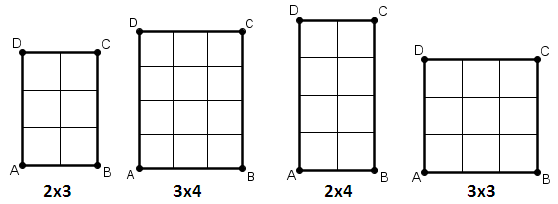
*שימו לה המשחק האינטראקטיבי נתמך java ולכן אינו עובד בדפדפן Chrom.

תמר והדר שיחקו בכל השולחנות הללו ושאלו שאלות מעניינות.

2. האם ישנם שולחנות דומים?
א. תמר שמה לב כי הכדורים בשולחנות 1x2 , 2x4 מתנהגים באופן דומה. הסבירו.
    התוכלו למצוא שולחן נוסף מסוג זה? תוכלו להיעזר במשחק האינטראקטיבי.
ב. הדר טענה שיש בקבוצה זוג אחר של שולחנות דומים. התוכלו לומר מיהם?
    האם יש קשר בין מימדי השולחנות שמצאתם? אם כן מהו?
ג. תנו דוגמה לשולחנות נוספים בעלי התנהגות דומה. בדקו במשחק האינטראקטיבי.

3. האם ניתן לדעת מראש את מספר הפגיעות (כולל ההתחלה והסיום) עד שיגיע הכדור לעצירה?
א. מהו השולחן בעל מספר הפגיעות הקטן ביותר?
    התוכלו לדעת מהו השולחן בעל מספר הפגיעות הגדול ביותר?
ב. הדר מצאה שני שולחנות שונים שבהם מספר הפגיעות (כולל ההתחלה והסיום) הוא 5. מיהם?
ג. תמר סברה כי גם בשולחן 1x4 מספר הפגיעות הוא 5. האמנם?
    האם יש קשר בין מימדי השולחנות שמצאתם ומספר הפגיעות? אם כן מהו?
ד. הדר ביקשה לבדוק האם החוקיות שמצאה אכן עובדת גם במקרים נוספים.
    היא חיפשה שולחנות בהם מספר הפגיעות הוא 7.
    מצאו, בעזרת המשחק האינטרקטיבי, שולחנות נוספים שבהם מספר הפגיעות הוא 7. (hits=7)
    בדקו האם הקשר שמצאתם בין מימדי השולחנות ומספר הפגיעות אכן עובד.

ה. תמר מצאה כי גם בשולחן במימדים של 6x8 מספר הפגיעות הוא 7. הכיצד?
    האם יש צורך לנסח מחדש את החוקיות?
ו. אם ברשותכם שולחן דמיוני של 150x300, התוכלו לדעת מראש מה יהיה מספר הפגיעות?

שחקני הביליארד המקצוענים יודעים כי מהלך מוצלח דורש תכנון מפורט של מסלול הכדורים מבחינה גיאומטרית ופיסיקלית, כמו גם ביצוע מדויק להפליא. 
בולצמן, מענקי הפיסיקה של המאה ה- 19, טען שהתנהגות מולקולות גז בקופסה דומה להתנהגות כדורי הביליארד ולפיה בנה את הבסיס לתורת המכניקה הסטטיסטית, שמהווה אחת מאבני היסוד של הפיזיקה המודרנית. בעקבותיו, במאה ה- 20, התפתחה תיאוריה מתמטית החוקרת את מסלולי הכדורים בביליארד כמערכת דינמית הנשלטת על ידי חוקי התנועה של ניוטון, ואיך האקראיות לכאורה קשורה לתורת הכאוס. קראו עוד על החוקרת בתחום במכון וייצמן, פרופ' ורד רום-קידר.

המתמטיקאים חוקרים מסלולי הכדור גם בשולחנות שאינם מלבניים כמו משולש, אליפסה או תיבה.
קראו עוד ב- Math World

4. האם ניתן לדעת מראש באיזו פינה הכדור יעצור?
הדר ותמר הביאו את המשחק לכיתה.
בכדי לשכלל את המשחק, הן הוסיפו ניקוד לכל משחקון לפי הניקוד הבא:

• כדור שיעצר בפינה A - 100 נקודות
• כדור שיעצר בפינה B - 50 נקודות
• כדור שיעצר בפינה C - 25 נקודות
• כדור שיעצר בפינה D - 10 נקודות

א. באפשרותכם לבחור את גודל השולחן למשחקון. באיזה שולחן תבחרו בכדי לקבל ניקוד הכי גבוה?
ב. אם ברשותכם שולחן דמיוני של 150x300, התוכלו לדעת מראש בכמה ניקוד תזכו?

לשם חקירת החוקיות, תוכלו לרכז את תוצאות המשחקונים בטבלה הבאה:

שאלות חקירה נוספות:

• האם קיים קשר בין אורך המסלול הכדור עד לעצירתו לבין מימדי השולחן?
• אילו סוגי סימטריה ניתן למצוא במסלול הכדור בשולחנות השונים?
  לאילו שולחנות ניתן למצוא סימטריה שיקופית לקו אנכי?
  לאילו שולחנות ניתן למצוא סימטריה שיקופית לקו אופקי?
  לאילו שולחנות ניתן למצוא סימטריה סיבובית?
• העלו גם אתם שאלות נוספות לחקירה של שולחנות הביליארד.

מקור הפעילות - Paper Pool: Analyzing Numeric and Geometric Patterns - NCTM, illuminations