המרכז הארצי למורים למתמטיקה בחינוך העל יסודי

2. מן הפנים אל החוץ

א. נתונות שלוש נקודות A, B, C שהן אמצעי הצלעות של משולש כלשהו, אך המשולש המקורי עצמו
(DEFD) נעלם. בדקו ביישום הדינאמי האם וכיצד ניתן ליצור את משולש DEFD:

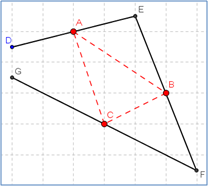- האם תמיד ניתן לבנות את המשולש על פי אמצעי צלעותיו?
- כיצד ניתן לבנות את המשולש המקורי? תארו את הבנייה ונמקו.
- האם קיים רק משולש אחד כזה?
- בהינתן שיעורי נקודות האמצע, התוכלו למצוא את שיעורי קודקודי המשולש המקורי.

ב. נתונות ארבע נקודות A, B, C, D שהן אמצעי הצלעות של מרובע כלשהו, אך המרובע המקורי עצמו
(EFGH) נעלם. בדקו ביישום הדינאמי האם וכיצד ניתן ליצור את המרובע EFGH:

- האם תמיד ניתן לבנות את המרובע על פי אמצעי צלעותיו? אם כן, באיזה תנאי?
- כיצד ניתן לבנות את המרובע המקורי? תארו את הבנייה ונמקו.
- האם קיים רק מרובע אחד כזה?

ג. האם וכיצד ניתן לבנות מחומש מחמש הנקודות של אמצעי הצלעות?

האם וכיצד ניתן לבנות משושה משש הנקודות של אמצעי הצלעות?

על כנפי הדמיון

תקציר| הנקודה שבפנים| نقطة في الداخل

1. חלוקת שטחים

במגרש כדורגל הציב השופט את הכדור בנקודה P בתוך הריבוע וחילק את שטח המגרש לשתי הקבוצות באופן הבא:

קבוצה א תקבל את השטח הכתום S1+S3.

קבוצה ב תקבל את השטח הסגול S2+S3.

תוכלו להיעזר ביישום הדינאמי לשם החישובים עבור נקודות P שונות.

א. היכן לדעתכם יש למקם את הנקודה P כך שהחלוקה תהיה הוגנת? מדוע?

ב. כיצד תשתנה החלוקה (אם בכלל) אם המגרש יהיה מלבני? נמקו.

שוב תוכלו להיעזר ביישום הדינאמי לשם שינוי מימדי המלבן.

ג. כיצד תשתנה החלוקה (אם בכלל) אם הנקודה תהיה מחוץ למגרש? נמקו.

2. חלוקת נפחים

נתונה תיבה מלבנית ובתוכה נלכד עכביש בנקודה P שהיא מרכז התיבה. העכביש מתח חוטים לפינות התיבה כך שיצר פירמידות אשר קודקוד הראש שלהן הנקודה P ובסיסן פאות

התיבה.

א. כמה פירמידות נוצרו באופן זה?

ב. מה תוכלו לומר על סכום הנפחים של שתי פירמידות נגדיות (שבסיסן מונח על פיאות נגדיות).

ג. כיצד ישתנו הנפחים אם הנקודה P תנוע למקום אחר במרחב התיבה? נמקו.הנחיה – ניתן להיעזר בפתרון השאלה הקודמת.

3. המרחק הנעלם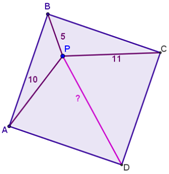

במגרש כדורגל ריבועי נמצא השחקן בנקודה P.

ידוע לו כי מרחקו מפינת המגרש בקודקוד A הוא 10מטרים, מהקודקוד B הוא 5 מטרים ומהקודקוד C הוא 11 מטרים. בשאלות הבאות תוכלו להיעזר ביישום הדינאמי .

א. התוכלו לעזור לו ולקבוע מהו מרחקו מפינת המגרש בקודקוד D?

ב. כיצד ישתנה המרחק PD כאשר המגרש יהיה מלבני?

ג. מה יהיה המרחק PD אם השחקן יהיה מחוץ למגרש?

ד. מה יהיה המרחק PD אם נתון כי: PB=a ,PA=c ,PC=b?

4. תיבה

נתונה תיבה ובתוכה נלכד עכביש בנקודה P. העכביש מתח חוטים לפינות התיבה כך ש:

PA=13 ,PB=5 ,PD=15 ,PE=23.

התוכלו למצוא את המרחק של העכביש מפינת התיבה PG) G) ?

הנחיה – ניתן להיעזר בפתרון השאלה הקודמת.

שטחים בריבוע

תקציר|שטחים בריבוע

1. ריבוע סוב סוב

הריבוע האדום מסתובב סביב מרכז הריבוע הכחול, כך שאחד מקודקודי הריבוע האדום מונח במרכזו של הריבוע הכחול. ראו את היישום הדינאמי .

א. אם שני הריבועים שווים בגודלם, הראו כי בכל כוון שהוא הריבוע האדום מכסה רבע משטחו של הריבוע הכחול.

ב. אם נגדיל את הריבוע האדום, האם עדיין השטח שהוא יכסה יהיה רבע משטח הריבוע הכחול? נמקו.

ג. אם נקטין הריבוע האדום, האם עדיין השטח שהוא יכסה יהיה רבע משטח הריבוע הכחול?
אם כן, באיזה מקרה? אם לא, מדוע?

2. טנגרם

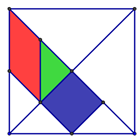במשחק טנגרם המפורסם מחולק הריבוע,
שאורך צלעו 12 ס"מ, לשבעה חלקים.חשבו את השטחים הצבועים של:
  א.      הריבוע
  ב.      המשולש הקטן
  ג.       המקבילית

שחקו במשחק הטנגרם האינטראקטיבי.

ועוד ברקנים מאלף אפס - איזה שטח גדול יותר, האדום או הכחול?

3. ריבוע בריבוע

א. על כל אחת מצלעות ריבוע שאורך צלעו יחידה, הקצו נקודת אמצע, ויצרו ריבוע פנימי. (ראו איור)
הסבירו מדוע המרובע הפנימי הוא ריבוע.
מצאו את שטחו.
(רמז- נסו לבנות פאזל)