תקציר| ממוצעי פיתגורס ועוד| פתרון| حلول

האגדה מספרת שפיתגורס, המתמטיקאי היווני הנודע מימי יוון הקדומה ( 500 לפנה"ס), עבר פעם ליד חרש ברזל והתאהב בצלילי דפיקות הפטיש שהיו נעימים לאוזנו. הוא בדק ומצא, כי משקלי הפטישים היו 6, 8, 9, ו-12 ק"ג. היחסים בין משקלי הפטישים הפיקו צלילים הרמוניים.

 מה מיוחד כל כך במספרים אלה? שאל.

הוא מצא כי הממוצע החשבוני בין 6 ל-12 הוא   

ואילו הממוצע ההרמוני בין 6 ל-12 הוא   

פיתגורס בדק גם כלי פריטה וגילה שקיים קשר מתמטי בין אורך המיתר, שעליו פורטים, ובין גובה הצליל: כשמתקיים יחס מסוים בין אורכי המיתרים, נוצרת הרמוניה בין הצלילים. כך הפך פיתגורס לראשון שהראה כי יש קשר הדוק בין מדע מדויק לבין מוסיקה.

1. מהירות ממוצעת

א. לטיול השנתי נסענו באוטובוס בכביש המהיר. בשל עומס כבד בתנועה נסע האוטובוס לאיטו במהירות של 40 קמ"ש חצי מהדרך. ובחצי השני של הדרך הצליח להגביר את מהירותו ל-80 קמ"ש. האם מהירותו הממוצעת בדרך כולה הייתה 60 קמ"ש? יותר, או פחות?

ב. באיזו מהירות היה צריך האוטובוס לנסוע בחצי הדרך השנייה בכדי שמהירותו הממוצעת תהיה 80 קמ"ש?

ג. מכונית עברה דרך של 40 ק"מ במהירות ממוצעת של 40 קמ"ש. מה צריכה להיות מהירותה הממוצעת ב-40 הק"מ הבאים כדי שמהירותה הממוצעת לאורך כל 80 הק"מ תהיה 80 קמ"ש?

2. ממוצעים בין מלבן וריבוע

נתון מלבן שמידותיו x ו-y. נשאל את עצמנו שאלות אחדות:

א. מה צריך להיות אורך צלע הריבוע שהיקפו ישווה להיקף המלבן?

ב. מה צריך להיות אורך צלע הריבוע ששטחו ישווה לשטח המלבן?

ג. מה צריך להיות אורך צלע הריבוע שאלכסונו ישווה לאלכסון המלבן?

ד. מה צריך להיות אורך צלע הריבוע שהיחס בין שטחו להיקפו ישווה ליחס בין שטח והיקף המלבן?

הידעתם?

כאשר חוקרים את תפקודם הביולוגי של גופים חיים יש חשיבות עיקרית לא לנפח הגוף בפני עצמו, או לשטח חיצוני של הגוף בפני עצמו, אלא ליחס שבין הנפח לשטח הגוף. באותה מידה בצורות שטוחות יש חשיבות ליחס שבין שטח הצורה להיקפה. למשל, מדינה שקו הגבול שלה ארוך מאוד ביחס לשטחה יש לה בעיות ביטחוניות מסובכות. באיזה ממוצע כדאי להשתמש?

3. מי גדול יותר?

נכיר ארבעה ממוצעים בין שני מספרים a ו- b הנפוצים ביותר. 
שלושת הראשונים נקראים ממוצעי פיתגורס.

א. חשבו את ארבעת הממוצעים השונים בין המספרים 4 ו-12 ובין 9 ו-16. 
סדרו את הממוצעים על פי גודלם. 
בדקו ביישום הדינאמי.

ב. הסבירו על פי האיור הבא מדוע הממוצע החשבוני גדול מן הממוצע הגיאומטרי.

ג. הסבירו על פי היישום הדינאמי מדוע האורכים A, G ו-H הם שלושת ממוצעי פיתגורס של האורכים a ו-b. 
מי גדול ממי?

ד. הוכיחו כי: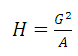 

ה. הוכיחו באיור כי: 

ו. סדרו את ארבעת הממוצעים על פי גודלם.

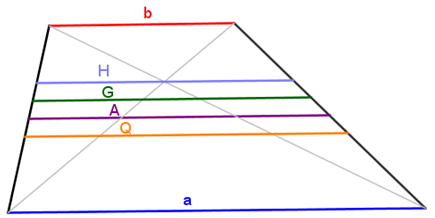4. ארבעה ממוצעים בטרפז

הוכיחו כי:

1. קטע אמצעים בטרפז שווה לממוצע החשבוני של בסיסי הטרפז.

2. קטע מקביל לבסיסי הטרפז המחלק לשני טרפזים דומים שווה לממוצע הגיאומטרי של בסיסי הטרפז.

3. קטע מקביל בטרפז העובר דרך מפגש אלכסוניו שווה לממוצע ההרמוני של בסיסי הטרפז.

4. קטע מקביל לבסיסי הטרפז המחלק לשני טרפזים שווי שטח, שווה לממוצע הריבועי של בסיסי הטרפז.

מקורות והרחבה: 

שלושת הממוצעים – פרופ' אביטל - גליונות לחשבון מס 7

על ממוצעים שונים – פרופ' אביטל – גליונות לחשבון מס 62

ממוצעים ומוסיקה – מייקל נ. פריד – על"ה 30, 2003

שבעה ממוצעים שונים בטרפז – נתן ויזדום - אוניברסיטת ג'ורג'יה

הוכחות ויזואליות ללא מילים (כמעט) - אורית זסלבסקי, גרייסי ויניצקי.  

• בעיות תנועה
• פתרון גרפי

 תקציר| בתנועה מתמדת| פתרונות| حركتنا مستم ّرة

1. שני חברים יצאו לדרך, בים בם בום.... 

תמי וניר שכנים בבית משותף ולומדים באותה כיתה. כל בוקר הם יוצאים יחדיו ברגל מביתם בשביל המוביל לבית הספר. יום אחד הם התחילו ללכת ביחד באותו קצב (v₁).

ניר המשיך ללכת באותה המהירות מחצית מהזמן ולאחר מכן הלך במהירות איטית יותר (v₂) עד הגיעו לבית הספר. לעומתו תמי המשיכה באותה מהירות חצי מהדרך (v₁), ובמחצית השנייה של הדרך, האטה והלכה במהירות האיטית של ניר (v₂).

א. התוכלו לקבוע מי הגיע ראשון לבית הספר?

ב. אם היו תמי וניר מתחילים במהירות איטית יותר, ולאחר מכן מגבירים את הקצב.
   מי אז היה מגיע ראשון לבית הספר ?

הנחיה – תארו את הבעיה במערכת צירים והיעזרו ביישום הדינאמי.

2. ארבעה כלי רכב יצאו לדרך 

אופניים, טרקטור, אופנוע ומכונית נסעו בכביש דו סטרי, כל אחד מהם במהירות קבועה משלו.

המכונית עקפה את הטרקטור בשעה 12:30 , חלפה על פני האופניים בשעה 13:00 ופגשה את האופנוע בשעה 13:30. האופנוע פגש את הטרקטור ב- 13:45 וחלף על פני האופניים בשעה 14:15.

באיזו שעה נפגשו האופניים והטרקטור?

הנחיה – תארו את הבעיה במערכת צירים והיעזרו ביישום הדינאמי.
הוכיחו את טענתכם גם באופן אלגברי.

3. חידת הנזיר  

נזיר הינדי יצא מכפרו עם שחר והחל לטפס לאיטו בשביל התלול, המוליך אל המנזר שעל פסגת ההר. הנזיר הספיק להגיע למנזר, לתפילה בשעת השקיעה.

למחרת עם שחר, בדיוק באותה שעה, שהחל לטפס ביום קודם, יצא הנזיר מהמנזר והחל יורד במהירות אל הכפר לאורך אותו שביל. הוא עצר למנוחת צהריים במעיין והמשיך והגיע אל ביתו בכפר בשעת השקיעה.

האם יתכן כי בשני הימים היה מקום שאליו הגיע הנזיר בדיוק באותה שעה גם בעלייה וגם בירידה? 

מקורות: 

• "שאלות מילוליות במשתנה אחד בגישה הגרפית" ,שוש גלעד, הוצאת מטח, 2000 
• nrich

פיצוחים נוספים בנושא בעיות תנועה:

מרוץ מכוניות דינאמי - בפיצוח הפנייה לסימולציה של בעיית תנועה, למאמר העוסק בסגנונות למידה שונים, ובעיות תנועה רבות בספר האלקטרוני "לראות מתמטיקה- פונקציות" של מטח.

בעיות בתנועה בדרך אחרת - הפיצוח עוסק בפתרון בדרכים לא שגרתיות של בעיות תנועה ברמה של 4-5 יח"ל. התנועה מתוארת בגרפים של פונקציות, וסיפור הבעיה ופתרונו נקרא מתוך הגרף.

בעיית תנועה - כוונים מנוגדים - עיבוד של שאלת בגרות ברמת 3 יח"ל, מתוך מאגר היישומים הדינאמיים.

מהר יותר, גבוה יותר וחזק יותר – בעיות תנועה מתוך מציאות האולימפיאדה. שימו לב כי הבעיות מנוסחות קצת אחרת מספרי הלימוד, ובחלקן יש להניח הנחות שאינן נתונות בשאלה, או לחפש נתונים שלא מופיעים בה.

תקציר| מהר יותר, גבוה יותר וחזק יותר

שימו לב כי בחלק מהבעיות עליכם להניח הנחות שאינן נתונות בשאלה, או לחפש נתונים שלא מופיעים בה.

	במשחקים האולימפיים ב-2008, דרישות הסף לריצת 200 מטר לנשים הייתה 11.32 שניות. כיצד תוכלו להשוות מהירות זו למהירות של מכונית ?
	באולימפיאדת בייג'ינג ב-2008, זכתה האצנית שלי-אן פרייזר מג'מייקה, בריצת 100 מטר לנשים, בזמן של 10.78 שניות.  אם היא הייתה ממשיכה לרוץ עוד 100 מטרים, בכמה היא הייתה משיגה אצנית שעמדה בתנאי הסף (11.32 שניות) ?
	דמיינו כי אתם מתחרים בריצת 200 מטר עם יוסיין בולט. בכמה מטרים הוא ישיג אתכם? (אם בכלל...)
	באליפות העולם לאתלטיקה 2009, שבר האלוף האולימפי יוסיין בולט, את שיא העולם בריצת 100 מטר וקבע זמן של 9.58 שניות. בולט שיפר את השיא שקבע הוא בעצמו באולימפיאדת ביג'ין 9.69 שניות. בכמה מטרים השיג בולט את עצמו?
	באימון שחיה לקראת אולימפיאדת לונדון ב-2012, שני שחיינים שוחים משני קצוות מנוגדים של הבריכה, במהירות קבועה אך שונה זה מזה. בפעם הראשונה נפגשו 30 מטר מקצה האחד של הבריכה. בפעם הבאה נפגשו 20 מטר מהקצה השני של הבריכה. מה אורכה של הבריכה ומתי יפגשו שוב?
	במרוץ אופניים בזירה סגורה במסלול הוולדרום (מלבן ושני חצאי עיגול), רוכב A מסיים סיבוב שלם כשהוא על הקו הכחול.  באותו זמן סיימו סיבוב גם רוכב B אשר רכב 1 מטר פנימה מהקו הכחול ורוכב C שרכב 2 מטר מחוץ לקו הכחול. איזה מרחקים שונים רכבו רוכבי האופניים? מיהו הרוכב המהיר ביניהם  ומהי מהירותו?

מקור הפעילות: "מתמטיקה וספורט – הספירה לאחור לאולימפיאדה 2012":
Maths and Sport: Countdown to  the Games, 
מאמרים ופעילויות בנשוא ספורט ומתמטיקה מאת אוניברסיטת קיימבריג', אנגליה.

   מקורות נוספים לפעילויות של ספורט ומתמטיקה: 

מתוך הפיצוח יום פאי שמח: "מרוץ הפאי", פעילות על תכנון מסלול המירוצים באולימפיאדה.

"מתמטיקה וספורט – הספירה לאחור לאולימפיאדה 2012":
Maths and Sport: Countdown to the Games, מאמרים ופעילויות בנושא ספורט ומתמטיקה מאת אוניברסיטת קיימבריג', אנגליה. 

מתמטיקה וספורט – Math and sport, פרק מתוך הספר The Mathematical Collage, אשר בא להמחיש את הקשר של מתמטיקה לחיי היום יום.

מתמטיקה וספורט – אוסף פעילויות, פוסטרים ומאמרים מתוך חודש המודעות המתמטית 2010 Mathematics Awareness Month, . 

על הדגל האולימפי – פעילות בהסתברות וקומבינטוריקה ועוד, מאת מחוז תל אביב 

על הלפיד האולימפי – אוסף פעילויות על מסלול הלפיד וענפי הספורט השונים באולימפיאדה, מאת מחוז תל אביב 

?Can Mathematics Help Usain Bolt Run Faster – כתבה ב- Science Daily, הצעות מתמטיות לאצן האולימפי כיצד לשפר את שיאי העולם שקבע. 

Math in Basketball – פעילות אינטראקטיבית מלווה בסרט וידאו המסביר כיצד ניתן לתכנן את הקליעה המושלמת לסל בעזרת המתמטיקה.