תקציר| הפסיכולוגיה של המבצעים |الحملة المربحة 

מן העיתונות : הפסיכולוגיה של מבצעי הנחות

בכדי לעודד מכירות, ולפתות לקוחות לקנות מוצר מסוים, סוחרים יוצאים במבצע ומציעים אותו במחיר מוזל. אך למעשה הם מפסידים מכך. כך עולה ממחקר חדש שפורסם בכתב עת של שיווק (Journal of Marketing).

חוקרים , מאוניברסיטת מינסוטה בדקו את עמדות הצרכנים כלפי מדיניות הנחות. הם מצאו, שקונים מעדיפים לקבל תוספת חינם מאשר לקבל משהו זול יותר. הסיבה העיקרית לכך שרוב האנשים מתקשים בהבנת שברים ואחוזים. צרכנים מתקשים לעתים קרובות להבין , למשל, כי הגדלת הכמות ב- 50% שווה בערכה להנחה של 33% במחיר. הנחקרים העדיפו באופן גורף הגדלת הכמות על הוזלה במחיר. בניסוי, החוקרים מכרו 73% יותר קרם ידיים כשזה הוצע בחבילת בונוס מאשר כאשר הוצע במבצע הוזלה שווה ערך (גם לאחר שניטרלו השפעות אחרות, כגון הרצון לאגור) . תפיסה שגויה זו נשארה בעינה גם כשהמוצר היה בהנחה משמעותית. בניסוי אחר, הציעו שתי עסקות על מכירת פולי קפה : 33% כמות נוספת חינם או 33% הנחה על המחיר. הצעת ההנחה כדאית הרבה יותר, אך הקונים ראו את שתי ההצעות כשוות ערך.

מחקרים אף הראו דרכים אחרות שבהן סוחרים עלולים לנצל את חרדת המספרים של הצרכנים. אחת הוא לבלבל עם מבצעי הנחה כפולים. אנשים נוטים להעדיף מוצר שהופחת ב -20% , ולאחר מכן על ידי הנחה נוספת של 25% , יותר מאחד שהיה נתונה לשווה ערך, חד פעמי , הנחה של 40%.

1. קופסת דגנים של 500 גרם עולה 25 ש"ח.

המבצע הענק: קופסת הדגנים הוגדלה ב- 50% והמחיר נשאר 25 ש"ח.

המבצע החם: מחיר קופסת הדגנים הוזל ב- 50%.

 איזה מבצע כדאי יותר לדעתך?

       א. חשבו מה מחיר הדגנים ל-100 גרם.

       ב. מה מחיר הדגנים ל-100 גרם במבצע הענק. (לאחר הגדלת הכמות) ?

       ג. מהו אחוז ההנחה במבצע הענק של הגדלת הכמות ב- 50% ?

       ד. מה מחיר קופסת הדגנים לאחר ההוזלה במבצע החם ?
       מה מחיר הדגנים ל-100 גרם במבצע החם לאחר ההנחה?

       ה. לאחר חישוביך – קבעו מהו המבצע המשתלם ונמקו.

        ו. הציעו דרכים נוספות לפתרון.

2. קופסת מיץ תפוזים של  250 מ"ל עולה 5 ₪.

המבצע הענק: קופסת המיץ הוגדלה ב- 40% והמחיר נשאר 5 ש"ח.

המבצע החם: מחיר מיץ התפוזים הוזל ב- 25%.

איזה מבצע כדאי יותר לדעתך?

      א. חשבו מה מחיר מיץ התפוזים לכל יחידת מ"ל בכל אחד מהמבצעים.

      ב. מהו אחוז ההנחה במבצע הענק של הגדלת הכמות ב- 40% ?

      ג. לאחר חישוביך – קבעו מהו המבצע המשתלם ונמקו.

3. חפיסת שוקולד של 100 גרם עולה 10 ש"ח.

המבצע הענק: חפיסת השוקולד הוגדלה ב- 50% והמחיר נשאר 10 ש"ח.

התבקשת ממנהל החנות לתכנן את המבצע כך שמחיר ההנחה במבצע הענק של הגדלת הכמות ב- 50% יהיה שווה ערך למחיר השוקולד במבצע החם. 
באיזה אחוז יש להוזיל את חפיסת השוקולד?

4. חבילת עודיות של 200 גרם עולה 10 ש"ח.

מבצע פיצוץ: חבילת העוגיות הוזלה ב- 10%, ויום לאחר מכן הוזלה שוב ב- 30%.

מבצע חגיגה: חבילת העוגיות הוזלה ב- 40%.

איזה מבצע כדאי יותר לדעתך?

 חשבו את מחיר חבילת העוגיות בכל אחד מהמבצעים.
לאחר חישוביך – קבעו מהו המבצע המשתלם ונמקו.

עובד ע"פ MatheMatics teacher | Vol. 107, No. 4 • November 2013

מקורות נוספים:

משימות אוריינות בנושא אחוזים

מבצעים חמים – אחוזים- יחידת לימוד בעריכת יעקב לדור, סמינר אורנים

תקציר| דמיון ברחבי העולם| פתרונות| בערבית 

1. הפירמידה במצריים

תאלס היה פילוסוף ומתמטיקאי יווני, מהמאה ה-7 לפנה"ס. תאלס היה הראשון שראה את הצורך בחשיבה דדוקטיבית וחקר את רעיון ההוכחות הגיאומטריות. הוא מפורסם בשני משפטים גיאומטריים שנקראו על שמו, משפטי תאלס, האחד קשור לדמיון והשני למעגל.

הפירמידה הגדולה בגיזה שבמצריים, הידועה גם בשם הפירמידה של ח'ופו, הפרעה שבנה אותה, היא אחת משבעת פלאי תבל. רבים ניסו בעת העתיקה לאמוד את גובהה ללא הצלחה, אך תאלס (600 לפנה"ס) חישב את גובהה של הפירמידה באמצעים פשוטים ובעזרת הידע המתמטי שלו.

נשכב על החול ביום שמש ליד הפירמידה ובקש שיסמנו בחול את גובהו. לאחר שסמנו את גובהו בחול הוא נעמד בתחילת הסימון כך שגופו יצר צל לאורך הסימון על החול ומעבר לסימון. באותו זמן יצרה הפירמידה אותה ביקש למדוד צל משלה.

תאלס אמר לנלווים אליו:
"כאשר צילי יגיע לגובהי המסומן, מדדו את צל הפירמידה."

הם מדדו ומצאו שאורך צל הפירמידה 145 מ'. מה גובה הפירמידה? 

הסבירו את שיטת מדידתו של תאלס. 

2. בעית המיתרים של בסקרה – הודו

בסקרה (Bhaskra) אסטרונום ומתמטיקאי הודי מהמאה ה-12. מפורסם בפיתוח שיטות לפתרון משוואות ריבועיות ועוד, חיבר כללים לפעולות במספרים חיוביים ושליליים ואף הציג שתי הוכחות יפות ופשוטות למשפט פיתגורס בעזרת דמיון משולשים. 

בין שני עמודים בגובה 15 מטר ו-10 מטר,נמתחו מיתרים באלכסון. בנקודת המפגש בין המיתרים הוצב עמוד תומך. 
לא ידוע המרחק בין העמודים.

ג. אם ידוע שגובה שני העמודים a ו-b. הביעו באמצעות a ו-b את גובה העמוד התומך.  

3. התעלה בסאמוס (יוון)

באי סאמוס היפהפה שביוון העתיקה (הידועה כיום בשם פיתגוריה..), בעיר הנמל החשובה לא היו מספיק מים לתושבים ולצבא, אך היה שפע של מים בהרים. בשנת 530 לפנה"ס, נחפרה תעלה באורך של קילומטר דרך ליבו של הר אבן קשה (ההר קסטרו). שני צוותי חפירה התקדמו זה מול זה משני קצות התעלה והצליחו להיפגש באמצע כמעט ללא טעות. החופרים השתמשו בפטישים ואיזמלים בלבד, ולא היה ברשותם מצפן, מפה טופוגרפית או כל מכשיר ניווט אחר. זוהי משימה מאתגרת גם כיום עם יכולות הטכנולוגיה המודרנית. מהנדס חפירת התעלה, יאופלינוס (Eupalinos) השתמש בתכנון אך ורק בגיאומטריה ובפתרון פשוט ומפתיע הצליח לתת לשני צוותי החפירה את הזווית המדויקת בה יחפרו. כיצד עשה זאת?

הבעיה שהתמודד איתה אופלינוס היה לקבוע את הכוון של כל צוות חפירה. לשם כך ערך סיור רגלי מסביב לאי בין המעין שבהר עד לעיר הנמל בקצה השני, כשהוא הולך בקווים ישרים ואנכים זה לזה. הוא מדד את אורכי קטעי המסלול שלו, וכך הצליח לדמיין משולש ישר זווית עם הזווית המבוקשת.

א.   מה מתאר סכום הניצבים האנכיים?

ב.   כיצד ניתן למדוד את הניצב האופקי של המשולש?

ג.   כיצד קבעו היוונים זווית ישרה?

      יש הסוברים שהשתמשו בשני מקלות באורכים שווים וסימון האמצע של כל אחד מהם.
      הסבירו כיצד עובדת השיטה?

הרחבה:
השיטה המצרית למשולש ישר זווית: משולש מצרי (בעיה 4 בפיצוח קיפולי נייר גיאומטריים)

4. דמיון בסין

ראשית נכיר את עקרון "משני הצדדים". 

א. הנקודה E היא נקודה כלשהי על אלכסון המלבן ABCD. מעבירים מהנקודה E קטעים המקבילים לצלעות המלבן.
מה הקשר בין שטחי שני המלבנים שנוצרו (DHEG  ו- FEIB )? 
הזיזו את הנקודה E ביישומון, בדקו והוכיחו השערתכם.

ב. הראו כי המשולשים  ΔAFE~ΔEIC

ג. השתמשו בעקרון "משני הצדדים" (שוויון השטחים) בכדי לחשב את היחס a/b באמצעות h₁ ו-h₂.

ד. פתחו את עקרון "משני הצדדים" גם עבור מקבילית. 
    הראו כי המשולשים ΔAFE~ΔEIC דומים, וחשבו את היחס a/b באמצעות h₁ ו-h₂.
    נסחו משפט לגבי יחס הגבהים במשולשים דומים.

תוכלו להיעזר ביישומון. 

5. להשקיף על אי בים – סין

המתמטיקה הסינית שימשה את מהנדסי האימפריה הסינית במדידות של שטחי שדות, בהכנת לוח השנה, לצרכים צבאיים, נווט וכדומה. המתמטיקאי הסיני ליו הואי, בן המאה ה-3, כתב את הספר "תשעת הפרקים של אמנות המתמטיקה", ובאחד הפרקים כתב מדריך מתמטי לאי בים, הכולל בעיות שונות בנווט ופתרונן המתמטי.

כיצד נמדוד את גובהו של צוק הררי בלב ים ?
ליו הואי פיתח שיטה הנקראת "הפרש כפול" למדידת עצם רחוק מבלי להגיע אליו, בעזרת עקרון "הפנים חוץ".

"העמדתי שני מוטות באורך 3 מטרים במרחק של 1000 צעדים זה מזה, כך שיהיו בקו ישר עם האי. הלכתי אחורה 123 צעדים מהמוט הראשון עד שראיתי את קצה המוט וקצה הסלע בקו אחד. כך גם צעדתי 127 צעדים מהמוט השני. כך הצלחתי למדוד את הגובה של הסלע באי ומרחקו מהמוט. "

התוכלו גם אתם למדוד את גובה הסלע?

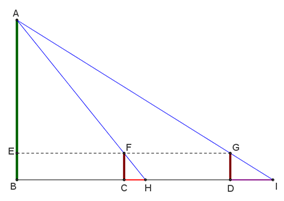א.  השלימו את משולש AHI למקבילית. העבירו מהנקודה G שעל אלכסון המקבילית, מקבילים לצלעות. סמנו את המשולשים הדומים שהתקבלו.

ב.  חשבו את אורכי צלעות המשולשים בעזרת הפרשי האורכים הנתונים. היעזרו ביישומון

ג.  חשבו בעזרת עקרון "משני הצדדים" את גובה הסלע AB.

ד.  הכלילו את השיטה.

מקורות נוספים:

• ההנדסה של האימפריה, סרט של ערוץ ההיסטוריה על בניית תעלת סאמוס. (בערך 7 דקות)

פיצוחים בנושא דמיון: 

• פרויקט עולמי למדידת היקף כדור הארץ
• ממוצעי פיתגורס ועוד
• על כנפי הדמיון
• אני דומה לעצמי

 תקציר| מה לעז ולגיאומטריה?| ما للعنزة والهندسة؟

1. במרכז שדה ריבועי 5x5 מ"ר, קשורה בחבל עז רעבתנית, האוכלת כל עשב הנקרה בדרכה.

א. מה צריך להיות אורך החבל כך שתאכל רק חצי מהשדה? מהי צורת השטח שתאכל העז? 
התנסו ביישומון 

ב. מהו אורך החבל הגדול ביותר שניתן לקשור בשדה זה? איזה חלק של השדה תאכל אז העז?

2. בתוך שדה רחב נמצא שטח מרוצף ריבועי שאורך צלעו 2 מטר. אל קצות השטח קשורה עז בלולאה בחבל באורך 1 מטר. 
העז מסתובבת סביב השטח המגודר ואוכלת את כל העשב אליו היא מגיעה.

התנסו ביישומון,

הזיזו את הלולאה של החבל סביב, וענו:

א. מהי צורת השטח שתאכל העז? חשבו את השטח של העשב הנאכל. הסבירו.
ב. בשדה אחר העז הרעבתנית נקשרה לשטח בצורת מחומש משוכלל שאורך צלעו 2 מטרים. מהי צורת השטח שתאכל העז הפעם? חשבו את השטח של העשב הנאכל. הסבירו. 
ג. כיצד ישתנה השטח שתאכל העז אם השטח יהיה בצורת משושה משוכלל שאורך צלעו 2 מטרים? משולש שווה צלעות? 
ד. הכלילו מהי צורת השטח שתאכל העז סביב שטח בצורת מצולע משוכלל בעל n צלעות? הביעו את שטחו בעזרת n.

3. במרכז שדה נמצא שטח מגודר מלבני ומרוצף בגודל 4x6 מ"ר. עז רעבתנית קשורה האחת הנקודות על הצלע CD. 
נסו לשער בכל אחד מהמקרים הבאים את צורת השטח שתאכל העז ואת שטחה. 
בדקו ביישומון.

א. העז קשורה אל הקודקוד C בחבל שאורכו 3 מטרים, 4 מטרים, 5 מטרים, 10 מטרים. 
ב. העז קשורה אל אמצע הצלע CD בחבל שאורכו 3 מטרים, 4 מטרים, 5 מטרים, 10 מטרים. 
ג. היכן לדעתכם נקשרה העז, אם צורת השדה שהתקבלה כבאיור הבא. 
ד. אורך החבל 10 מטרים, היכן יש לקשור את העז על הצלע CD, כך שיתקבל שטח מקסימלי?