תקציר|  דלתוני ריצוף| לדפי גזירה| פתרונות והנחיות

1. פירוק והרכבה של משולש שווה-צלעות

לפניכם משולש שווה צלעות. כידוע גובה במשולש שווה-צלעות מחלק אותו לשני משולשים חופפים. (מדוע?)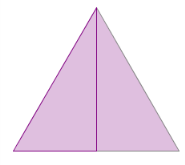  

גזרו משולש שווה צלעות והרכיבו מחדש את שני המשולשים על ידי הצמדת שני קדקודים של משולש אחד לשני קדקודים של המשולש השני.

כמה מצולעים שונים תוכלו להרכיב בדרך זו?

2. דלתון הריצוף

אחת הצורות שניתן ליצור באמצעות הצמדת המשולשים היא דלתון. 

דלתונים מיוחדים אלה נקראים דלתוני-ריצוף בגלל האפשרות ליצור

בעזרתם ריצופים של צורות גאומטריות רבות ואף של המישור כולו.

א. מהן התכונות המיוחדות של דלתונים אלה?

1. מהן מידות הזויות של דתלוני-ריצוף?
2. מצאו קשרים בין אורכי האלכסונים של הדלתון לבין אורכי הצלעות.

ב. גזרו מדפי הגזירה מספר דלתונים ונסו להרכיב באמצעותם מצולעים שונים, כך שדלתוני הריצוף נצמדים לאורך צלע שלמה.

1. אילו מהצורות הבאות ניתן להרכיב משולש, מרובע, מחומש, משושה?
2. אילו מצולעים משוכללים הצלחתם לבנות? הסבירו כיצד.

נסו להרכיב את המצולעים ביותר מאשר דרך אחת.

ג. הציעו דרכים שונות לרצף משטח בעזרת דלתוני הריצוף.

3. משושים

בבית הספר “חופים” יש חצרות פנימיות בצורת משושה. במסגרת פרוייקט לשיפור פני בית הספר עלתה הצעה
ליצור משטחים משושים באמצעות אריחי קרמיקה בצורת דלתוני ריצוף .

בקטלוג הגלריה לאריחים מצאו את הדגם שבתמונה וניסו לברר:

א. פי כמה גדול היקף המשושה החיצוני מהיקף המשושה הפנימי?
פי כמה גדול השטח?

ב. האם ניתן לבנות את ריצוף הקרמיקה באמצעות אריחים בשני צבעים בלבד, מבלי שלאריחים באותו צבע תהיה צלע משותפת?

ג. האם ניתן לבנות את ריצוף הקרמיקה באמצעות אריחים בשלושה צבעים בלבד מבלי שלאריחים באותו צבע תהיה צלע משותפת?

ד. האם ניתן להמשיך את הריצוף ולקבל משושה עוד יותר גדול הבנוי מאותם האריחים?
לכמה אריחים נוספים תזדקקו?

 4. ריצוף באריחים בשני גדלים

לפניכם שני אריחים לריצוף. שני דלתוני ריצוף כך שהצלע הקצרה בדלתון הגדול שווה באורכה לצלע הארוכה בדלתון הקטן.

א. מה יחס ההיקפים בין שני הדלתונים? מהו יחס השטחים?

ב. הצמידו את שני אריחי הדלתונים זה לזה. איזה מרובע התקבל? תארו תכונותיו.

ג. נסו להרכיב מצולעים שונים מדלתוני ריצוף אלו.

ד. האם ניתן לבנות דלתון ריצוף דומה גדול יותר המורכב משני אריחים אלו?

5. ריצוף באריחים בגדלים משתנים

תלמידי מגמת האמנות רוצים ליצור עיטור מיוחד לקיר מבנה המגמה בעזרת דלתוני ריצוף.
בהצעה ניתן להשתמש בגדלים שונים של דלתוני ריצוף.

התקבלו שתי הצעות:
הקבוצה של חן הציעה לבנות עיטור של פרח, והקבוצה של נוי הציעה לבנות עיטור משושה.

א. תארו את בניית הריצוף בכל אחת מההצעות.

ב. תכננו (בשרטוט או במילים) כיצד ניתן להוסיף שכבה נוספת לכל אחד מהעיטורים. לכמה דלתונים תזדקקו להוספת שכבה?

בעת שקילת ההצעה יש לבדוק בכל אחד מהעיטורים:

א. האם קיים יחס קבוע בין היקפי השכבות ?

ב. פי כמה גדול שטח האריחים הסגולים משטח האריחים בתכלת ?

ג. האם נוכל להגדיל את העיטור על ידי הוספת שכבות של דלתוני ריצוף?

ד. האם נוכל להוסיף שכבות נוספות של דלתוני ריצוף גם כלפי פנים?

ה. האם נוכל באופן זה למלא את כל השטח הלא מרוצף?

ו.  האם ניתן למלא את כל השטח הפנימי בדלתוני ריצוף בדרך אחרת?

קישורים 

דלתוני ריצוף בויקיפדיה

עוד ריצופי דלתונים בבלוג math humbre

היצירה Fractal Tessellation of Spirals שלהאמן Robert Fathauer מבוססת על דלתוני ריצוף

תקציר| לרבע את הירח

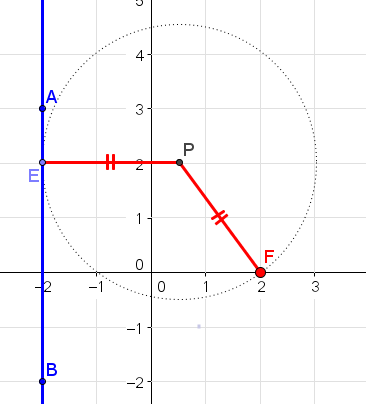
אחת הבעיות שהעסיקו את המתמטיקאים מאות בשנים, היתה כיצד ניתן "לרבע" את המעגל, כלומר כיצד ניתן לבנות בעזרת סרגל ומחוגה ריבוע ששטחו כשטח מעגל נתון. בניסיונתיהם הרבים, ניסו גם לרבע צורות מעגליות כגון סהרונים.

"סהרון" היא צורה החסומה על ידי שתי קשתות מעגליות, בדומה לירח.    

1. לרבע את הסהרון של היפוקרטס

א. עקבו ביישומון אחר שלבי הבנייה ותארו במילים כיצד בנה היפוקרטס את הסהרון. רשמו את הנתונים באופן מתמטי.

ב. הראו כי שטח המעגל הקטן שווה לחצי משטח המעגל הגדול.              

ג. מה היחס בין שטח של הסהרון ושטח המשולש ?
חשבו את שטח הסהרון בעזרת חיבור וחיסור שטחים.

ד. בנו ריבוע ששטחו כשטח הסהרון.

2. לרבע את המעגל- האמנם?

היפוקרטוס טען כי "הוכיח" שניתן לרבע את המעגל, (לבנות ריבוע ששטחו שווה לשטח המעגל)

למרות שכיום ידוע שלא ניתן לעשות זאת. במה טעה היפוקרטס?


 

א. הראו כי :  שטח ששת הסהרונים - שטח המשושה = שטח המעגל הקטן היעזרו בחיבור וחיסור שטחים.

ב. משושה, בהיותו מצולע, ניתן לרבע, כלומר לבנות ריבוע בעל שטח שווה. היפורקטס הראה שניתן לרבע סהרונים.
מכאן ניתן להסיק שניתן לרבע את המעגל... האמנם? במה טעה היפורקטס?

3. לרבע את הסהרונים של אלחאסן

אלחאסן סרטט את שני סהרונים באיור הבא בעזרת שלושה חצאי מעגלים.

א. עקבו ביישומון אחר שלבי הבנייה ותארו במילים כיצד בנה את הסהרונים. רשמו את הנתונים באופן מתמטי.

ב. מה היחס בין שטח של שני הסהרונים ושטח המשולש ?

ג. בנו ריבוע ששטחו כשטח שני הסהרונים.

מקורות נוספים:

מי הפך את הירח לריבוע? – עטרה שריקי, קשר ח"ם

מצגת "לרבע את המעגל", רקע היסטורי ומתמטי. (באנגלית)

תקציר| לקפל פרבולה 

הגדרה גיאומטרית:
פרבולה היא המקום הגיאומטרי של כל הנקודות שמרחקן מנקודה קבועה (המוקד) וישר קבוע (המדריך) שווה.

1. בעזרת קיפולים של דף נייר ונקודה אחת עליו נוכל ליצור באורח פלא פרבולה.
ללא סרגל, מחוגה או כל כלי מדידה...

על דף נייר: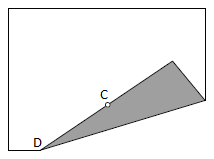 

-  סמנו נקודה C בקרבת אחת משפות הדף.
-  סמנו נקודה D על שפת הדף אליה התייחסתם קודם.
-  קפלו את הדף כך שהנקודה C תתלכד עם הנקודה D.
-  פתחו את הקפל וסמנו נקודה D אחרת על שפת הדף.
-  שוב קפלו את הדף כך שהנקודה C תתלכד עם הנקודה שסימנתם על שפת הדף.
-  חיזרו על התהליך עוד מספר פעמים.כדי לראות את התמונה שיוצרים הקפלים באופן ברור מומלץ לעבור עליהם בעזרת עפרון וסרגל.

מה קיבלתם?

- השוו את הנייר המקופל שלכם עם זה של חברכם. תארו את הדומה ואת השונה.

- קחו נייר נוסף, סמנו נקודה בתוכו במקום שונה וחזרו על התהליך. מה קיבלתם הפעם?

שאלות למחשבה:

א. ראינו כי הקיפולים יוצרים את המתאר של הפרבולה. מהם לדעתכם המוקד והמדריך?
ב. מה ניתן לומר על היחס הגיאומטרי בין הנקודות C,D וישר הקיפול ?
ג. מה ניתן לומר על ישר הקיפול ביחס לפרבולה ?
ד. אם נזיז את הנקודה C קרוב יותר לשפת הדף כיצד תשתנה הפרבולה? כיצד תשתנה הפרבולה אם נרחיק את הנקודה משפת הדף? 

 Thinking out loud 

2. לשחק בקיפולים:
בכדי להבין את הפלא ובכדי שנוכל לחקור מצבים שונים היעזרו ביישומון (קובץ גאוגברה להורדה).
א. גררו את הנקודה D והפעילו עקבות אחר הקיפולים. מה קיבלתם? מה ניתן לומר על כל קיפול ביחס לפרבולה? 
ב. בודאי שמתם לב כי הקיפול משיק לפרבולה, התוכלו לשער היכן נקודת ההשקה? כיצד נקודת ההשקה קשורה לנקודה D?
ג. צרו ביישומון פרבולות שונות על ידי שינוי מיקום הנקודה C.

1. כיצד תשתנה הפרבולה אם נמקם את C קרוב יותר לשפת הדף?
2. כיצד תשתנה הפרבולה אם נמקם את C רחוק יותר משפת הדף?
3. כיצד תשתנה הפרבולה אם נמקם את C על שפת הדף?
4. כיצד תשתנה הפרבולה אם נמקם את  C מתחת לשפת הדף?

3. כיצד נוכיח כי קיפולי הנייר יוצרים פרבולה?

נתבונן באיור הבא המייצג את קיפולי הנייר של הפרבולה: 

א. הסבירו מדוע CM=MD.
ב. הקו המקווקו מייצג את קו הקיפול. מה תוכלו לומר עליו ביחס ל- CD?
ג. נבנה אנך לישר המייצג את שפת הדף דרך הנקודה D. הסבירו מדוע CP=DP .
ד. הראו על פי ההגדרה הגיאומטרית של הפרבולה כי הנקודה P על הפרבולה.
ה. ציינו מיהו המדריך ומיהי נקודת המוקד.

4. עוד משחקי פרבולה

לפניכם יישומון לבניית הפרבולה כמקום הגיאומטרי.

א. הסבירו איזו תכונה מקיימת הנקודה P ביחס לישר המדריך ולנקודת המוקד.
ב. קרבו והרחיקו את נקודת המוקד מהמדריך. כיצד תשתנה הפרבולה?
ג. שנו את מיקום המדריך באופנים שונים. כיצד תשתנה הפרבולה?
ד. צרו, אם ניתן, בעזרת היישומון את הפרבולות הבאות: y²=-x, y=x² , y²=x+1
מצאו את המוקד והמדריך של כל פרבולה

נקודה למחשבה:
כיצד יראה המקום הגיאומטרי אם המדריך לא יהיה ישר אלא מעגל?

מקורות נוספים:

• הפרבולה כצורה גיאומטרית – חמוטל דוד, על"ה 29.
• Famous Curves Index– מדור באתר The MT History of Mathematics archive ובו רשימת עקומים מפורסמים במתמטיקה עם הסבר היסטורי ומתמטי וכן יישומים דינאמיים מדגימים.
• אוגדן למורה: גיאומטריה אנליטית - פעילויות ממוחשבות – מחשבמטיקה, מכון וייצמן