כתב עת על"ה

תקציר|מן הפנים אל החוץ 

2. מן הפנים אל החוץ

א. נתונות שלוש נקודות A, B, C שהן אמצעי הצלעות של משולש כלשהו, אך המשולש המקורי עצמו 
(DEFD) נעלם. בדקו ביישום הדינאמי  האם וכיצד ניתן ליצור את משולש DEFD:

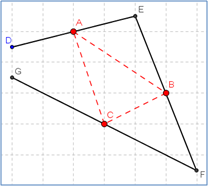- האם תמיד ניתן לבנות את המשולש על פי אמצעי צלעותיו?
- כיצד ניתן לבנות את המשולש המקורי? תארו את הבנייה ונמקו.
- האם קיים רק משולש אחד כזה?
- בהינתן שיעורי נקודות האמצע, התוכלו למצוא את שיעורי קודקודי המשולש המקורי.

ב. נתונות ארבע נקודות A, B, C, D שהן אמצעי הצלעות של מרובע כלשהו, אך המרובע המקורי עצמו 
(EFGH) נעלם. בדקו ביישום הדינאמי  האם וכיצד ניתן ליצור את המרובע EFGH:

- האם תמיד ניתן לבנות את המרובע על פי אמצעי צלעותיו? אם כן, באיזה תנאי?
- כיצד ניתן לבנות את המרובע המקורי? תארו את הבנייה ונמקו.
- האם קיים רק מרובע אחד כזה?

ג. האם וכיצד ניתן לבנות מחומש מחמש הנקודות של אמצעי הצלעות?

האם וכיצד ניתן לבנות משושה משש הנקודות של אמצעי הצלעות?

על כנפי הדמיון

משושה פרחוני

תקציר| משושה פרחוני

בפיצוח זה נשרטט ונתבונן בעין מתמטית בפרחים המרהיבים הללו, בעלי שישה עלי כותרת.

את המשושה הפרחוני תוכלו לצבוע ולעטר ברכות "שנה טובה" או לקשט את הסוכה.

נשרטט את הפרחים בעזרת עפרון ומחוגה או כלי עגול אחר (כגון מכסה או צלחת). ניתן גם לשרטט בתוכנה גיאומטרית (כגון הגאוגברה). מצורפות הוראות שלב אחר שלב.
תוכלו לצפות בבנייה בסרטון הבא.

 א. המשושה הנסתר

1.  הסבירו מדוע חסום בפרח משושה משוכלל (שכל צלעותיו שוות).  רמז - התבוננו במרובע החסום בין שני מעגלים. 

2. חשבו מהי הזווית הפנימית של המשושה.

3. מהו שטח המשושה אם ידוע שרדיוס המעגל הפנימי שווה ל- R ס"מ.

ב. שני משושים בפרח

1. הקיפו את הפרח במעגל. מהו רדיוס המעגל? הסבירו.

2. חיברו את נקודות ההשקה של המעגל המקיף והמעגלים הקטנים. הסבירו מדוע נוצר משושה.

3. מהו יחס שטחי המשושים הללו?

ג. עלי הכותרת

1. שערו מהו היחס בין שטחי עלי הכותרת הסגולים לבין שטח העיגול הפנימי והיחס בין שטחי עלי הכותרת הורודים לשטח העגול הפנימי.

2. חשבו את השטח של עלה כותרת סגול אחד, אם ידוע שרדיוסו של המעגל הפנימי שווה ל- R ובדקו את השערתכם בסעיף א. 

(ניתן להיעזר בנוסחת השטח של גזרת מעגל ברדיוס R וזווית מרכזית  ברדיאנים: R=1/2R²)

3. חשבו את השטח של עלה הכותרת הורוד  ושוב בדקו השערתכם מסעיף א.

קישורים  נוספים:

משימה פרחונית – פיצוח העוסק בחישובי שטחים

יצירת מגן דוד – פעילות יצירה סביב המגן דוד, בנייה בעזרת סרגל ומחוגה ושאלות מתמטיות.

סרטון המציג יצירת עטיפה לדיסק פרחונית ומדליקה – היכן כאן חבוי המשושה הפרחוני?

תקציר|על כנפי הדמיון

1. אדריכל גן המשחקים

א. בשכונת "על כנפי הדמיון" הוקם גן משחקים חדש ובו מתקני ספורט ואתגרים. הגן בנוי מרצף של שלשה מתחמים ריבועיים. המרחק בין שתי הפינות המנוגדות של הגן הוא 100 מטר (ראו בשרטוט AD). אדריכל הגן תכנן לשתול ארבעה עצים שיפרשו צל בגן בנקודות: A, B, C ו-D (ראו איור).
חשבו מה המרחק בין העצים.
רמז - השתמשו ביחס הדמיון של משולשים דומים.

ב. בשלב ב של הקמת הגן, הורחב המגרש לשישה מתחמים ריבועיים. אדריכל הגן תכנן להוסיף ולשתול ארבעה עצים שיפרשו צל בגן בנקודות: E, F, G ו-H (ראו איור).
חשבו מה המרחק בין העצים הפעם.

ג. עץ נוסף נשתל בנקודה K (ראו איור).
חשבו מה המרחק בין העצים.

ד. הגנן פרש חבלים במתחם הגן על פי הוראות האדריכל. הוא היה מעוניין לחשב את הזווית שנוצרה בקודקוד B. מצאו את הזווית.
רמז- היעזרו בקווי העזר שבאיור.

מן הפנים אל החוץ

תקציר|טיול רציונלי ללונה פארק - חלק ב'

האתגר של "הרפתקת הלייזר"  

אחד המתקנים המאתגרים בלונה פארק הוא "הרפתקת הלייזר", קליעה למטרה באמצעות אקדח לייזר ייחודי לעבר מטרה נסתרת. קבוצת חובבי המתמטיקה החליטו לפצח את האתגר

באמצעות כישוריהם המתמטיים ולנסות לזכות בפרס הגדול.

במשחק זה יש לפגוע במטרה המוצבת על קיר בגובה 1 מטר מעל הרצפה. אך המטרה מוסתרת ולא ניתן לפגוע בה באופן ישיר.

על השחקן לבחור באיזה מרחק מהקיר להעמיד את אקדח הלייזר ולכוונו אל מראה ניידת הניצבת 10 סנטימטרים מעל הרצפה ומוצבת במצב התחילי 30 סנטימטרים מהקיר.

קרן הלייזר הפוגעת במראה, מוחזרת ממנה (באותה זווית) ופוגעת בקיר. 

לכל שחקן ושחקנית ניתנת הזדמנות אחת לפגוע במטרה. אם הצליחו, תינתן הזדמנות נוספת לפגוע במטרה נוספת, הפעם בגובה 1.5 מטרים. מי שמצליח לפגוע בשתי המטרות יזכה בפרס

הגדול! לאחר שכמה מחברי הקבוצה ניסו לפגוע במטרה ללא הצלחה ונפסלו, טכסו עיצה החברים וחיפשו משוואה מתמטית שתאפשר להם למצוא את המיקום הנכון להעמיד את אקדח

הלייזר.

תוכלו להיעזר ביישום הדינאמי  של "הרפתקאות הלייזר":

א. באיזה גובה תפגע קרן הלייזר אם נעמיד את האקדח במרחק 100 ס"מ מהקיר? 150 ס"מ? כיצד מצאתם?

ב. באיזה גובה תפגע קרן הלייזר אם נעמיד את האקדח במרחק 30 ס"מ מהקיר? כיצד תסבירו את התוצאה?

ג. השלימו את הטבלה. 

ד. מהי הפונקציה המתארת את גובה הפגיעה כתלות במרחק האקדח מהקיר? תארו את התנהגותה. (תוכלו לעקוב אחר הנקודות ביישום הדינאמי )

ה. באיזה מרחק יש להעמיד את אקדח הלייזר כך שיפגע במטרה בגובה 1 מטר? ובאיזה מרחק יש להעמיד את אקדח הלייזר כך שיפגע במטרה בגובה 1.5 מטר? הסבירו כיצד מצאתם. בדקו ביישום הדינאמי האם הצלחתם לפגוע במטרה?

ו. היכן יפגע הלייזר , אם נעמיד את אקדח הלייזר במרחק 30 סנטימטר מהקיר? התוכלו להסביר את התופעה?

ז. סמנו את הנקודות המתאימות במערכת הצירים ושרטטו את הגרף המתאר את עלות הטיול לתלמיד כתלות במספר המשתתפים. הרחיבו את הגרף של הפונקציה גם לתחום המספרים השליליים.

ח. בשלב המתקדם של המשחק ניתן לגרור את המראה ולקבוע את מרחקה מהקיר. חברי הקבוצה החליטו להציב את המראה במרחק של 50 ס"מ מהקיר. תוכלו להזיז את המראה גם ביישום הדינאמי.

1. מהי כעת הפונקציה המתארת את גובה הפגיעה כתלות במרחק האקדח מהקיר? שרטטו את הגרף באותה מערכת הצירים (מהסעיף הקודם) תארו את התנהגותה ובמה היא שונה מהפונקציה הקודמת. 
   (תוכלו לעקוב אחר הנקודות ביישום הדינאמי)
2. באיזה מרחק יש להעמיד הפעם את אקדח הלייזר כך שיפגע במטרה בגובה 1 מטר? ובאיזה מרחק יש להעמיד את אקדח הלייזר כך שיפגע במטרה בגובה 1.5 מטר? הסבירו כיצד מצאתם. בדקו ביישום הדינאמי האם הצלחתם לפגוע במטרה?

   ---

מקורות נוספים

התנהגות פונקצית מנה סביב נקודת אי הגדרה – משולחנו של מורה, שושנה הלוי, רחל סילבצקי ואנה ספרד, על"ה 2

חקירת פונקציה רציונלית – קשר ח"ם , חקירה בעזרת מחשב – אוסף דפי עבודה לתלמיד , מאת דפנה אשרת ואלה שמוקלר, בהנחיית אורית זסלבסקי. func3.pdf , func4.pdf , func5.pdf , func6.pdf .

מנה של פונקציות לינאריות – יישום דינאמי המלווה בדף עבודה מאת מרכז המורים.

טיול רציונאלי ללונה פארק – חלק א'

תקציר| טיול רציונלי ללונה פארק - חלק א'

1. תכנון הטיול 

בבית ספרנו מתארגנת קבוצת "מועדון המתמטיקה" לצאת לטיול ללונה פארק. עלות הטיול, הכוללת הסעות ודמי כניסה קבוצתיים, היא 1200 שקלים. הוחלט כי עלות הטיול תתחלק באופן שווה בין כל התלמידים שיוצאים לטיול.

א. כמה ישלם כל תלמיד אם יצאו לטיול 10 תלמידים? 30 תלמידים?

ב. השלימו את הטבלה. 

ג. מהי הפונקציה המתארת את עלות הטיול לתלמיד?

ד. סמנו את הנקודות המתאימות במערכת הצירים ושרטטו את הגרף המתאר את עלות הטיול לתלמיד כתלות במספר המשתתפים. הרחיבו את הגרף של הפונקציה גם לתחום המספרים השליליים.

ה. כיצד תשתנה הפונקציה וישתנה הגרף בכל אחד מהמקרים:

תוכלו להיעזר ביישום הדינאמי .

      1. אם תתקבל תרומה של 900 שקלים לסיוע בהוצאות הטיול?

      2. אם כל תלמיד צריך לשלם בנוסף 10 שקלים עבור פיצה.

      3. אם הוחלט לממן 3 תלמידים בוגרים מהמועדון שילוו את הטיול.

ו. התקבלה תרומה מקרן חובבי המתמטיקה לעידוד פעילות מתמטיות מאתגרות והוחלט כי הקרן תשתתף בהוצאות הנסיעה לטיול. התרומה תתכן בשלוש אפשרויות שונות:

      1. מימון כל ההוצאות עבור 10 תלמידים.

      2. השתתפות בהוצאות בסה"כ של 500 שקלים.

      3. השתתפות בהוצאה של כל תלמיד ב-10 שקלים.

התאימו לכל גרף את הסיפור והפונקציה המתאימה לו. הסבירו באיזו תוכנית הייתם בוחרים ובאיזה מקרה. 

 מקורות נוספים

התנהגות פונקצית מנה סביב נקודת אי הגדרה – משולחנו של מורה, שושנה הלוי, רחל סילבצקי ואנה ספרד, על"ה 2

חקירת פונקציה רציונלית – קשר ח"ם , חקירה בעזרת מחשב – אוסף דפי עבודה לתלמיד , מאת דפנה אשרת ואלה שמוקלר, בהנחיית אורית זסלבסקי. func3.pdf , func4.pdf , func5.pdf , func6.pdf .

מנה של פונקציות לינאריות – יישום דינאמי המלווה בדף עבודה מאת מרכז המורים.

טיול רציונאלי ללונה פארק – חלק ב'

תקציר|אשליות מעגליות

באיזה פרח העיגול האדום גדול יותר?

 צפו ברמז לפתרון:

מהו מרכז המעגל ?

האם הנקודה הימנית או אולי הנקודה השמאלית היא מרכז המעגל?

 צפו ברמז לפתרון:

מישהו אכל לי מהעוגה...

אבל למעשה היא עדיין שם.

התוכלו למצוא את חתיכת העוגה הנעלמת?

צפו ברמז לפתרון:

אשליות אופטיות – אוסף אשליות מאת מתי"א חולון

מה שרואים מכאן לא רואים משם – מצגת על אשליות אופטיות מלווה בהסברים פשוטים.

מדוע כשמסתכלים על ספיראלה נראה שהיא זזה ולמעשה היא לא? - דוידסון אונליין - שאל את המומחה.

אל תאמין למראה עיניך שתי דוגמאות בהן קטעים שווים נראים שונים, וקו והמשכו נראים כבלתי רצופים. שמואל אביטל, גליונות לחשבון 51.

תעתועי ראיה אוסף אשליות אופטיות גיאומטריות, המרכז הארצי למורים יסודי.

תקציר|עיגולים ומעגלים|פתרונות

1. סידור המטבעות

חמישה מטבעות זהים נוגעים זה בזה, ומסודרים כך שמרכזיהם יוצרים שני משולשים שווה צלעות. (ראו איור)

הזיזו שני מטבעות בלבד, כך שבסידור החדש, עדיין המטבעות יהיו צמודים זה לזה ויצרו שני משולשים שווה צלעות שונים.

2. עיגולים על עיגולים

באיור עיגולים צבעוניים המסודרים בריבוע, באופן שהם מכסים חלקית זה את זה.

איזהו הצבע שתופס את השטח הגדול ביותר?

איזהו הצבע שתופס את השטח הקטן ביותר?

3. סבך הנחשים הצבעוניים

באיור ארבעה נחשים צבעוניים מתפתלים בין המעגלים: אדום, כחול, ירוק וסגול.

מבין הנחשים הצבעוניים מיהו הקצר ביותר?

מקור: http://www.puzzles.com