כתב עת על"ה

תקציר|בארץ יצורי הפרא המתמטיים |פתרונות|في بلاد الكائنات العجيبة الرياضية | حلول

בארץ יצורי הפרא המתמטיים חיים יחדיו שני סוגי יצורים  . 
אך כאשר שניהם פוגשים זה את זה הם בולעים זה את זה, לכן כשהם ביחד הם נקראים "זוג האפס".

היצורים הללו מתאספים יחד כדי להציג מספרים שלמים.

1. הנה שלושה מפגשים המייצגים את אותו מספר:

ציירו יצורים נוספים המייצגים את אותו מספר:

2. ושוב שלושה מפגשים המייצגים את אותו מספר. מהו?

ציירו יצורים נוספים המייצגים את אותו מספר.

3. איזה מפגש מייצג מספר גדול יותר?

4. יצורי הפרא המתמטיים יודעים גם להציג תרגילי חשבון, לדוגמה תרגיל חיבור:

 צפו בסרטון "חיבור בארץ יצורי הפרא המתמטיים" 

השלימו:

תוכלו לשחק ולפתור בעיות במשחק האינטראקטיבי של חיבור יצורי הפרא. (נדרש תוסף ג'אווה בדפדפן שאינו כרום)

5. יצורי הפרא המתמטיים יודעים גם להציג תרגילי  חיסור :

צפו בסרטון "חיסור בארץ יצורי הפרא המתמטיים".

השלימו:

6.  אך מה יעשו היצורים בתרגילי חיסור, כאשר לא ניתן "לקחת" מתוכם?  

     איך ניתן לקחת  ( -2) מתוך 5 ?

יצורי הפרא הנבונים הציעו להוסיף שני "זוגות האפס" כדי שאפשר יהיה לבצע את החיסור. 

השלימו:

קצת היסטוריה

הסינים היו הראשונים שהתייחסו למספרים השליליים כבר במאה השנייה לפני הספירה לשם חישובים מסחריים. הם ייצגו את המספרים החיוביים (זכות) עם מקלות שחורים והשליליים (חוב) עם מקלות אדומים.

במאה השמינית לספירה, ההודים שהכניסו את שיטת הספירה הערבית ואת האפס, התייחסו גם הם למספרים השליליים. המתמטיקאי ההודי ברַהמַגוּפְטַה כתב:"הסכום של שתי זכויות הוא זכות, של שני חובות הוא חוב, הסכום של זכות וחוב הוא ההפרש שלהם".

אך במשך מאות בשנים גרמו המספרים השליליים למתמטיקאיים מבוכה ואלו התקשו לקבלם וקראו להם "דמיוניים ושקריים ...".  רק במאה ה-19 התקבלו המספרים השליליים כחלק ממערכת המספרים כאשר המילטון, מתמטיקאי אירי ואחרים, ייסדו בסיס מתמטי מלא למערכת המספרים השליליים.

משחקים ועוד עם מספרים שליליים:

"שלושה ברצף" - משחק מדליק לתרגול חיבור וחיסור מספרים שליליים. ניתן לשחק עם חבר או נגד המחשב, וכן לקבוע את רמת המשחק. 

מעבדת הבטריות - משחק המלווה גם במערך שיעור. מודל נוסף להצגת המספרים השליליים המלווה במערך שיעור מאת ה- NCTM. 

"מאזניים לפתרון משוואות הכוללות מספרים שליליים" - משחק אינטראקטיבי לפתרון משוואות אלגבריות.

מקורות

• Nrich - Adding and Subtracting Positive and Negative Numbers
• Colored-Chip Model for Integers יחידת לימוד למורים מאת Annenberg Media להכרות עם המודל "אסימונים צבעוניים" לפעולות החשבון עם מספרים שליליים. ביחידה וידאו קצר ומומלץ של השתלמות מורים המציג את המודל ונשאלת שם השאלה האם המודל מתאים להצגת כל פעולה?
• הקניית המושג "מספרים מכוונים"- שילוב נימוקים חוץ ופנים מתמטיים - מיכאל קורן- על"ה 32.
• מתולדות המתמטיקה - על המספרים השליליים - שמואל אביטל, גליונות לחשבון 21.

תקציר|הפרש ריבועים | פתרונות| فرق مربعين | حلول

1. ללא מילים

לפניכם שלוש הוכחות דינאמיות ללא מילים להפרש שטח ריבועים.

הסבירו את האיורים הדינאמיים והראו בדרך אלגברית את נכונות הנוסחה:

(a²-b²)=(a-b)(a+b)

2. מטבעות הזהב

סוחר עשיר אסף מטבעות זהב. יום אחד נשאל "כמה מטבעות זהב יש לך?".

הסוחר הסס לרגע וענה ברמיזה: 

"אהההם...  אם אחלק את מטבעותיי לשני חלקים אז ההפרש ביניהם יהיה קטן פי 77 מהפרש הריבועים שלהם".

התוכלו לדעת כמה מטבעות זהב לסוחר?

3. מיהו המספר

העלו מספר דו ספרתי בריבוע, הפכו את סדר ספרותיו והעלו גם בריבוע. 

הפרש הריבועים יצא גם הוא ריבוע.

התדעו מהו המספר?

4. קסמי חשבון

א. בחרו שני מספרים עוקבים, חשבו את הפרש הריבועים שלהם.

    האם קיבלתם את סכום שני המספרים שבחרתם? הכיצד?

ב. בחרו שני מספרים הנבדלים זה מזה ב-2.

    חשבו את הפרש הריבועים שלהם ואת סכומם. התדעו מה הקשר? הסבירו.

ג. בחרו שני מספרים הנבדלים זה מזה ב-3.

    חשבו את הפרש הריבועים שלהם ואת סכומם. התדעו מה הקשר? הסבירו.

ד. התוכלו לדעת במה נבדלים שני מספרים זה מזה כאשר הפרש ריבועים שלהם גדול פי 77 מסכומם?

   (ע"פ המאמר - Revisiting a Difference of Squares, David Slavit, Mathematics Teacher, February 2001)

5. משחקים במחשבון

זיו שיחק במחשבון וקיבל כמה תוצאות מפתיעות:

65²-35²=3000

55²-45²=1000

85²-65²=3000

א. התוכלו למצוא עוד זוגות מספרים שהפרש הריבועים שלהם יתן כפולה של 1000?

ב. התוכלו למצוא שני מספרים שהפרש הריבועים שלהם 5000? 

ג. רון הצטרף לשעשועי החישובים ומצא גם הוא תופעה מפתיעה:

                       56²-45²=1111

                      89²-12²=7777

                      78²-23²=5555

ד. האם ניתן לקבל גם את המספרים הבאים 3333, 9999, 8888? הסבירו כיצד.

6. משפטון פרמה

פרמה, מתמטיקאי צרפתי נודע מהמאה ה-17,  עסק בתורת המספרים .

פרמה גילה כי כל מספר ראשוני הגדול מ-2 , ניתן להציג באופן אחד ויחיד כהפרש של שני ריבועים.התוכלו להוכיח?

רמז באיור המצורף ללא מילים:

 מקור: אתרו של דוד שי, המשפט האחרון של פרמה

למתעניינים, מקורות נוספים:

בעיה ופתרונה - גליונות לחשבון, שמואל אביטל

הוכחות ויזואליות: השקפותיהם ואמונותיהם של תלמידים- רז הראל וטומי דרייפוס, על"ה 41

תקציר|פונקציות פה ושם ובכל מקום- חלק ד'|دوال هنا وهناك في كل مكان

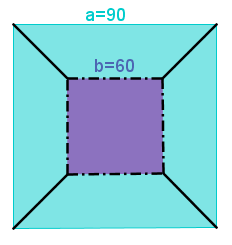
האקר הרשע וחבורת הרשת (סייבר) מתחרים זה בזה להגיע לראשו של מגדל גבוה בכדי להציל את פסל "הצליל הטוב". האקר בוחר לטפס במדרגות הגדולות בכדי להשמיד את הפסל. חבורת הרשת נאלצים לטפס

במדרגות קטנות יותר. הם חוששים שלעולם לא ישיגו את האקר. 

צפו  בסרט המצויר, מה דעתכם האם חבורת הרשת תצליח במשימה?

מרוץ המדרגות חלק א'          
תרגום הסרטון                

האקר וחבורת הרשת החלו בטיפוס המאתגר. עד מהרה הם שמו לב, שהמדרגות הקטנות שלהם גדלות בקצב אחר מהמדרגות של האקר הרשע. 

צפו  בסרט המצויר, מה דעתכם האם חבורת הרשת תצליח במשימה?

מרוץ המדרגות חלק ב'          

תרגום הסרטון               

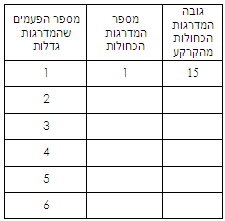
א. מלאו את הטבלה תוך כדי צפייה בסרט.

    המדרגות האדומות של האקר                                המדרגות הכחולות של חבורת הרשת
                        

ב.  סמנו על ציר ה-x את מספר הפעמים שהמדרגות גדלות (1-6).

     סמנו על ציר ה-y את מספר המדרגות.

     מתוך הטבלה שיצרתם, סמנו את הנקודות המתאימות את מספר הפעמים למספר המדרגות של האקר באדום. חברו נקודות אלו לגרף.

     מתוך הטבלה שערכתם, סמנו את הנקודות המתאימות את מספר הפעמים למספר המדרגות של חבורת הרשת בכחול. חברו נקודות אלו לגרף.

ג. 1) מה תוכלו ללמוד מהגרף על מרוץ המדרגות בין האקר לחבורת הרשת?

   2)  האם ניתן לראות בגרף שבתחילת המרוץ האקר השיג את חבורת הרשת?

   3) האם ניתן לראות בגרף מתי  חבורת הרשת השיגה את האקר?

   4) אם המדרגות של האקר וחבורת הרשת היו שוות בגודלן, מתי לדעתכם חבורת הרשת הייתה משיגה את האקר?

ד. ידוע כי גובה המדרגות של האקר היה 60 ס"מ ואילו גובה המדרגות של חבורת הרשת היה 15 ס"מ.

    בכדי למדוד מה היה הגובה שלהם מהקרקע נוסיף עמודה שלישית לכל טבלה. 

           המדרגות האדומות של האקר                           המדרגות הכחולות של חבורת הרשת
               

ה. העלו את ממצאכם על מערכת הצירים שלמטה וענו על השאלות הבאות:

   1). מה תוכלו ללמוד כעת מהגרף על מרוץ המדרגות בין האקר לחבורת הרשת?

   2).  האם ניתן לראות בגרף החדש מתי  חבורת הרשת השיגה את האקר?

   3).  מה מיוחד בנקודה בה שני הגרפים נפגשים?

   4).  מה היה גובהו של המגדל אשר בראשו היה פסל "הצליל הטוב" ?

   5). אם גובהו של המגדל היה 4 מטרים, מי היה משיג במרוץ?

ו. אם n  מייצג את מספר הפעמים שהמדרגות גדלו, מהו הביטוי המתאר את גובהן של המדרגות האדומות של האקר מעל הקרקע?  מהו הביטוי המתאר את גובהן של המדרגות הכחולות של חבורת הרשת מעל הקרקע?

מקור הסרטים והפעילות -

VITAL/Ready to Teach is a production of Thirteen/WNET. Major funding for this project was provided by the U.S. Department of Education.
© 2008 Thirteen/WNET

פיצוחים נוספים בנושא מבוא לפונקציות:

1. מכונות של פונקציה- תוך כדי משחק יכירו התלמידים את הפונקציה כמכונה ואף ירכיבו מספר פונקציות פשוטות.

2. בונים בקוביות - תוך כדי התנסות מוחשית בבנייה בקוביות התלמידים יבחנו תהליכי השתנות באמצעות בניית טבלה וגרף.

3. אגדה של פונקציה - התלמידים יכירו את האגדה המפורסמת "גרגר האורז" (אגדת השחמט) העוסקת בהפתעה של השתנות של גידול פי שניים. התלמידים יבחנו את קצב הגידול וישוו זאת לגידול לינארי ואחר.

תקציר|פונקציות פה ושם ובכל מקום- חלק ג' |פתרונות|دوال هنا وهناك وفي كل مكان

זהו סיפור עם מהודו הרחוקה על שליט עריץ ונערה חכמה שידעה קצת מסודות המתמטיקה.  

א. השלימו את הטבלה הדינאמית (גליון אקסל) וסמנו נקודות מתאימות במערכת הצירים באמצעות. 

ב. כמה גרגרי אורז יהיו לרני לאחר 5 ימים? כיצד ניתן לראות זאת בגרף? 

ג. כמה גרגרי אורז יהיו לרני לאחר שבוע? לאחר n ימים?

תקציר|פונקציות פה ושם ובכל מקום- חלק ב' |פתרונות|دوال هنا وهناك وفي كل مكان – الجزء الثاني

1. הפעם נשחק בקוביות ונבנה מבנים שונים של מדרגות. לפניכם "המדרגות התלויות":

א. השלימו את הטבלה הדינאמית (גליון אקסל) וסמנו נקודות מתאימות במערכת הצירים.

ב. האם תוכלו לדעת מתוך הגרף כמה קוביות נדרשות לבניית מדרגות בגובה 6?

ג. כמה קוביות לדעתכם צריך לבניית מדרגות בגובה 10? בגובה 100? בגובה n?

ד. מה אפשר לומר על השתנות מספר הקוביות עם עליית גובה המדרגות?

2. נבנה מדרגות בצורה שונה, "המדרגות הסימטריות".

א. השלימו את הטבלה הדינאמית (גליון אקסל) וסמנו נקודות מתאימות במערכת הצירים באמצעות.

ב. האם תוכלו לדעת מתוך הגרף כמה קוביות נדרשות לבניית מדרגות בגובה 6?

ג. מה אפשר לומר על השתנות מספר הקוביות עם עליית גובה המדרגות?

   במה שונה השתנות מספר הקוביות ב"מדרגות התלויות" מאשר ב"מדרגות הסימטריות" ? 

   כיצד ניתן לראות שוני זה בגרפים?    במה שונים ובמה דומים הגרפים?

ד. כמה קוביות לדעתכם צריך לבניית מדרגות בגובה 10? בגובה n ?

ה. הסבר נוסף לחוקיות הוא שניתן לבנות מהמדרגות מבנה ריבועי. הכיצד?  

    היעזרו באנימציה הבאה:

ו. עצבו בעצמכם מבנים נוספים של מדרגות ותארו את החוקיות, נסו להתאים לה גרף.

ז. אתגר-  במוזיאון הלאומי בוושינגטון מוצב פסל הפירמידה המרובעת של האמן היהודי אמריקאי סול לה-ויט.

 בנו גם אתם דגם של הפירמידה המרובעת. התוכלו לחשב כמה קוביות נדרשות לדגם?

  Sol LeWitt
Four-Sided Pyramid, 1999, first installation 1997
National Gallery of Art, Washington
לחצו על התמונה להגדלה

מעובד לפי מקור מתוך רשת המורים TES  -  Valley Maths 2004, D Cavill

פיצוחים נוספים בנושא מבוא לפונקציות:

1. מכונות של פונקציה- תוך כדי משחק יכירו התלמידים את הפונקציה כמכונה ואף ירכיבו מספר פונקציות פשוטות.

2. אגדה של פונקציה - התלמידים יכירו את האגדה המפורסמת "גרגר האורז" (אגדת השחמט) העוסקת בהפתעה של השתנות של גידול פי שניים. התלמידים יבחנו את קצב הגידול וישוו זאת לגידול לינארי ואחר.

3. הפונקציה בסרטים מצוירים- מרוץ המדרגות- התלמידים יעקבו אחר תהליך של השתנות בסיפור המוצג בסרט מצוייר, טבלה ובגרף.

תקציר|פונקציות פה ושם ובכל מקום- חלק א' | פתרונות|دوال هنا وهناك في كل مكان - الجزء الأول| حلول

א. בכוכב המתמטי מכונות משוכללות המייצרות מספרים סודיים. ניתן להכניס לתוכן מספרים ולקבל מספרים אחרים במקומם לפי חוקיות סודית. יצורי הכאוס פלשו לכוכב והחליטו לשבש את עבודת המכונות. 

הצילו את הכוכב! שחקו במשחק מכונת הפונקציות. עליכם לעצור את היצורים הנכנסים למכונה על ידי כך שתגלו את החוקיות של המכונה. התבוננו במספרים הנכנסים והיוצאים מהמכונה, הנרשמים בטבלה,  התוכלו למצוא את החוקיות?

התבוננו במכונה שבאיור:

1) מה יהיה פלט המכונה כאשר נכנס המספר 1?

2) מה יהיה פלט המכונה כאשר נכנס המספר 11?

3) איזה מספר נכנס למכונה אם יצא המספר 11?

4) כתבו ביטוי אלגברי המתאר מה יהיה פלט המכונה אם הקלט היה n.

היו זריזים, ומצאו את החוקיות של כל מכונה ועזרו להציל את הכוכב. (בחרו פעולה ולאחריה מספר)                                                                                                                                           

מקור המשחק - PBS                       

ב. בכוכב המתמטי יצאו בתוכנית הגנה והמציאו מכונות משוכללות אף יותר כך שבהן קשה יותר לגלות את החוקיות הסודית של המכונה. במכונות החדשות ניתןלהרכיב כמה רכיבים זה אחר זה. המכונה המורכבת עובדת כך שהמספר היוצא מהרכיב הראשון (הפלט מהשלב הראשון) עובר לרכיב הבא ונכנס אליו (הקלט של השלב הבא), וכך הלאה...

לפניך מכונה הבנויה משני רכיבים:

                                            
1) הכניסו למכונה את המספר 2 , איזה מספר לדעתכם תקבלו ביציאה? 

     חברו תרגיל חשבוני מתאים. 

2) הכניסו מספרים שונים למכונה ומלאו את הטבלה: 

3) התוכלו לדעת איזה מספר נכנס למכונה אם המספר הסודי שיצא ממנה הוא 100? 99?

4) יצורי הכאוס שיבשו את עבודת המכונה והפכו את סדר הרכיבים. 
    הכניסו כעת למכונה את המספר 2 , איזה מספר תקבלו ביציאה? חברו תרגיל חשבוני מתאים. 

בכוכב המתמטי החליטו להתחכם אף יותר ויצרו את מכונת "המספרים הסודית ביותר". 
המכונה החדשה מורכבת מחמשה רכיבים.

שחקו במכונה האינטראקטיבית ועקבו אחר פעולתה. 
בכל שלב בחרו מספרים בעזרת החיצים ופעולות מתוך ארבע פעולות החשבון.

השתמשו במכונה האינטראקטיבית כדי ליצור את המכונה המבצעת את התהליך הבא:

בחרו מספר (קלט)
      הכפילו אותו

      הוסיפו 2 לתשובה

      חלקו את התוצאה ב-2 

      חסרו ממה שקיבלתם 7 

      הכפילו את התוצאה ב-4

1) מהו המספר הסודי שתפלוט המכונה אם בחרתם כקלט את המספר 5? 
    חברו תרגיל חשבוני מתאים.

2) מהו המספר הסודי שתפלוט המכונה אם בחרתם כקלט את המספר 5- ? 
    חברו תרגיל חשבוני מתאים.

3) אם תבחרו כקלט את n מה יהיה הפלט ?

4) האם תוכלו להרכיב מכונת מספרים דומה אך פשוטה יותר? כלומר הרכיבו מכונה הפועלת לפי אותו תהליך המורכבת ממספר קטן יותר של רכיבים.

5) התוכלו לדעת איזה מספר נקלט במכונה אם המספר הסודי שנפלט ממנה הוא 120?
    ואם הוא 50?
    חברו תרגילים חשבוניים מתאימים המתארים כיצד מצאתם.

6) יצורי הכאוס הצליחו לפצח גם הפעם את הקוד הסודי... כיצד עשו זאת?
    אם ידוע כי המספר הסודי שנפלט מהמכונה הוא x, תנו ביטוי באמצעות x המתאר את הקלט.

אתגר לכיתה 

התוכלו להרכיב מכונה מחמישה רכיבים (עם ארבעת פעולות החשבון) שהקלטים שלה הם:

  2, -4, 0, 1, 5  כך שהמכונה תתן את הפלט הגדול ביותר?

בחרו אתם חמישה מספרים שונים ובנו מכונה אחרת בה הפלט יהיה המספר הגדול ביותר.

מקור הפעילות - Learning Math - פעילות מתוקשבת למורי חטיבת הביניים.

פיצוחים נוספים בנושא מבוא לפונקציה:

1. בונים בקוביות - תוך כדי התנסות מוחשית בבנייה בקוביות התלמידים יבחנו תהליכי השתנות באמצעות בניית טבלה וגרף.

2. אגדה של פונקציה - התלמידים יכירו את האגדה המפורסמת "גרגר האורז" (אגדת השחמט) העוסקת בהפתעה של השתנות של גידול פי שניים. התלמידים יבחנו את קצב הגידול וישוו זאת לגידול לינארי ואחר.

3. הפונקציה בסרטים מצוירים- מרוץ המדרגות- התלמידים יעקבו אחר תהליך של השתנות בסיפור המוצג בסרט מצוייר, טבלה ובגרף.

משחקים נוספים

מכונת פונקציות עם שלב אחד ועם שני שלבים.

משחקים מבית  Interactivate- Shodor

מכונה של פונקציות

מבחן הקו האנכי לפונקציה- האם אוסף הנקודות במערכת הצירים מתארת פונקציה?

חוק המלך- משחק ישן וחביב להורדה מבית מטח, עליכם לגלות את חוק המלך לעבור חדרים ולפתור חידות עד שתגיעו אל המלך.

Math Function Mania 2.6 - משחק להורדה, משחק להכרות עם פונקציות בו 20 רמות קושי. 
ניתן לשחק גם בזוגות.

צפו בסרט - Math Magic - קסם מתמטי- תן לי ואנחש את מספרך.

תקציר| זהו את הזהות הטריגונומטרית| פתרונות| ميّزوا المتطابقات المثلثية| حلول

1. זהויות טריגונומטריות לסכום זוויות

באיור הבא נתון DB=1.

א. איזה קטע באיור שווה ל- (sin(α+β ?   

    איזה קטע באיור שווה ל- (cos(α+β ? 

ב. שנו באיור הדינאמי את הזווית α באמצעות הקודקוד A,     

    כך שסכום הזוויות α+β  נשאר קבוע.   

    אילו גדלים משתנים באיור ואילו נשמרים? 

    האם מתקיים sin(α+β)=sinα+sinβ ?

    האם מתקיים cos(α+β)=cosα+cosβ ?

ג. שנו באיור הדינאמי את הזווית β באמצעות הקודקוד B,   

    כך שסכום הזוויות α+β למעשה משתנה.

    אילו גדלים משתנים באיור ואילו נשמרים? 

    האם מתקיים sin(α+β)=sinα+sinβ ?

    האם מתקיים cos(α+β)=cosα+cosβ ?

*  אילו זוויות α, β מקיימות sin(α+β)=sinα+sinβ ?

   ברצוננו להביע את (sin(α+β באמצעות sinα ו- sinβ בלבד. 

ד. הביעו את אורכי הקטעים:

GH, BF, HF, DG, DH, BH באמצעות β,α בלבד.      

ה. רשמו נוסחאות מתאימות:

_________________ = (sin(α+β

_________________ = (cos(α+β

ו. רשמו נוסחאות מתאימות לזווית כפולה:

_________________ = (sin(2α

_________________ = (cos(2β

מקור: הוכחות ויזואליות: השקפותיהם ואמונותיהם של התלמידים, רז הראל טומי דרייפוס, על"ה 41

2. זהויות טריגונומטריות לזווית כפולה

א. הסבירו מדוע זווית AOB> כפולה מזווית BAM>  

ב. עקבו באיור הדינאמי אחר השתנות הזוויות וערכי הסינוס שלהן. 

ג. הביעו את AM בשתי דרכים:

    1) בעזרת משולש ΔAOM  

    2) בעזרת משולש ΔABM 

    מה ניתן להסיק?  

ג. כיצד תוכיחו את הנוסחה כאשר הזווית AOB> קהה?

ד. הביעו את OM בשתי דרכים. מה תוכלו להסיק הפעם? 

מקור: NRICH

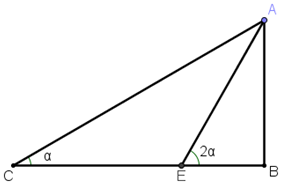3. עוד זהויות טריגונומטריות לזווית כפולה 

באיור הבא נתון CB=2.

נסמן t=tanα.

הביעו את אורכי צלעות המשולשים באיור באמצעות t.

הוכיחו באמצעות האיור את הזהויות הטריגונומטריות הבאות לזווית כפולה:

4. זהויות טריגונומטריות מפתיעות 

ידועה הנוסחה: 

נסמן tanα=t. הוכיחו את הזהויות ושימו לב לתופעה המפתיעה:

מה נקבל אם נרשום ממול כל אחד מהזהויות את המקדמים של t מהמונה ומהמכנה בסדר עולה?

מהי הנוסחה ל- (tan(5α?  ל- (tan(nα?

זהויות טריגונומטריות בשילוב גישת "מה אם לא?" - גילה רון, אורית זסלבסקי, קשר חם.

משחקים ודפי עבודה לתרגול בטריגונומטריה - NCTM