כתב עת על"ה

גלגלי המזל

תקציר| גלגלי המזל|  دواليب الحظ 

1. "גלגל אותה" פעילות אינטראקטיבית עם גלגל מזל, רולטה
2. בואו נתכנן גלגלי מזל
3. משחק התאמה בין גלגלי המזל וגרף העמודות- רמה קלה.
4. גלגלי המזל בעדלאידע - משחק התאמה בין גלגלי המזל וגרף העמודות - רמה בינונית
5. קישורים לפעילויות ומשחקים בנושא הסתברות

1."גלגל אותה"                                                                                                                     

במשחק "גלגל אותה" שני גלגלי מזל, הממוספרים מ- 1 עד 4. באפשרותכם לחבר או לחסר את שני המספרים. מספר המטרה שלכם הוא 3.

א. מהן כל האפשרויות לניצחון במשחק? כמה אפשרויות יש?

ב. מה לדעתכם הסיכוי לנצח במשחק? האם תבחרו בחיבור או בחיסור המספרים?

היישומון "גלגל המזל" – Nrich        

הדרכה 

ג. נסו את מזלכם בגלגל המזל.. סובבו ביישום האינטראקטיבי את שני גלגלי המזל וחברו את המספרים שהגרלתם.

     1. שחקו משחקון אחד, האם ניצחתם? שחקו 10 משחקונים, בכמה משחקונים ניצחתם? 
         הריצו את המשחק 100 משחקונים. בכמה משחקונים ניצחתם?

     2. איזה סכומים ניתן לקבל? איזה סכום הוא בעל הסיכוי הקטן ביותר להתקבל? 
         ואיזה סכום הוא בעל הסיכוי הגדול ביותר להתקבל?

     3. התבוננו בגרף העמודות, והסבירו מה מתארת כל עמודה.

     4. אם ניתנה לכם האפשרות לבחור במספר מטרה סכום לניצחון, איזה מספר הייתם בוחרים? 

ד. נסו שוב את מזלכם בגלגל המזל.. סובבו ביישום האינטראקטיבי את שני גלגלי המזל וחסרו את המספרים שהגרלתם.

     1. שחקו משחקון אחד, האם ניצחתם? שחקו 10 משחקונים, בכמה משחקונים ניצחתם? 
         הריצו את המשחק 100 משחקונים. בכמה משחקונים ניצחתם?

     2. איזה הפרשים ניתן לקבל? איזה הפרש הוא בעל הסיכוי הקטן ביותר להתקבל? 
         ואיזה הפרש הוא בעל הסיכוי הגדול ביותר להתקבל?

     3. התבוננו בגרף העמודות, והסבירו מה מתארת כל עמודה.

     4. אם ניתנה לכם האפשרות לבחור במספר מטרה הפרש לניצחון, איזה מספר הייתם בוחרים? 

מעובד על פי פעילות באתר Nrich

2. בואו נתכנן גלגלי מזל

א. בנו שני גלגלי מזל בהם הסיכוי לקבל סכום זוגי שווה לסיכוי לקבל סכום אי זוגי? הציעו זוגות שונים של גלגלי מזל.

ב. בנו שני גלגלי מזל בהם הסיכוי לקבל סכום זוגי גדול מהסיכוי לקבל סכום אי זוגי?

ג. בנו שני גלגלי מזל בהם הסיכוי לקבל הפרש זוגי שווה לסיכוי לקבל הפרש אי זוגי?

3. משחק התאמה

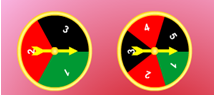
לפניכם שלושה זוגות של גלגלי מזל שיצרו את ארבעה גרפי עמודות. 
התאימו לכל זוג של גלגלי מזל את גרף העמודות המתאים לו. (שימו לב, האם מדובר בסכום או הפרש המספרים)

1. 

2. 

3.

4. גלגלי המזל בעדלאידע

ביריד העדלאידע יצרו זוגות שונים של גלגלי מזל מתוך הגלגלים מטה. באפשרותכם לבחור מתוכם זוג גלגלי מזל ולשחק את המשחק כאשר מספר המטרה הוא סכום המספרים שהגרלתם או הפרשם. אך גרפי העמודות השייכים לכל זוג התבלבלו... מי שייך למי?

5. קישורים

פעילויות נוספות

משחקי מזל בחנוכה – בפיצוח בעיות ברמות קושי שונות בהסתברות. בבעיה הראשונה משחק בו ניתן להתנסות עם יישום אינטראקטיבי.

פעילות בהסתברות וייצמן: זהירות 7 בדרך!: לתלמיד / למורה 

אי ודאות - משימות אוריינות, האגף לפיתוח תוכניות לימודים

מראשיתה של תורת ההסתברות – פרופ' אביטל , הסבר על מושג ההסתברות, ראשיתה של תורת ההסתברות בתקופת המתמטיקאים בליז פסקל ופייר פרמה ושימוש בה במשחקי מזל.

בעיה בהסתברות – והצעה לפתרונה באופן גרפי, גליונות לחשבון, פרופ' אביטל.

משחקים

סולמות ונחשים – שחקו בסולמות ונחשים, משחק אינטראקטיבי, עם גלגלי מזל (רמה 1) או שתי קוביות (רמה 2) וחקרו מה ההסתברות שלכם לטפס במעלה הלוח. הפעילות כוללת גם דפי עבודה , פתרונות ולוח משחק להדפסה. פעילות מאת Math Interactivities

משחקי מזל ביריד – משחק אינטרנטי (מותאם גם ל-IPAD) בו מספר שלבים. המטרה לזכות בכמה שיותר כרטיסים במשחקים בהם יש לחשב הסתברויות ברמות שונות. הכרטיסים יזכו אותך בכניסה ליריד בו עוד חמישה משחקי הסתברות שונים.

יישומונים להסתברות ניסויית

אוסף כלים אינטראקטיביים להגרלה – מטבע, קובייה, קלפים וגלגלי מזל. ניתן לבצע את ניסוי ההגרלה שוב ושוב ולראות את ההתאמה בין ההסתברות הניסויית להסתברות התיאורטית.

כלי אינטראקטיבי לבניית גלגל מזל צבעוני (הפעלת היישומון מומלץ להשתמש בדפדפן אקספלורר או להתקין בכרום את התוסף (החינמי)  (IE Tab

סרטונים בהסתברות

מהי ההסתברות למפולת שלגים? - סרטון ופעילות אינטראקטיבית לחקר ההבדל בין הסתברות ניסויית והסתברות תיאורטית והצגתן בגרף עמודות או טבלת שכיחות יחסית. מלווה בדף עבודה.

מהי ההסתברות למצוא דרכך במדבר? – סרטון אנימציה משעשע, תלת מימד, המסביר בפשטות והומור מושגי יסוד בהסתברות. 

 כפל בעזרת האצבעות- מטריקים בחשבון לאלגברה

תקציר|  כפל בעזרת האצבעות| פתרונות 

עוד משחר ההסיטוריה בני האדם משתמשים באצבעות הידיים לשם ספירה ופעולות חשבון.
בפעילות זו נכיר ונחקור כיצד אפשר לכפול בעזרת אצבעות הידיים.

כיצד כופלים ב-9 באמצעות האצבעות?

  כופפו את האצבע הרביעית                  אצבעותיכם מייצגות את המספרים 1 עד 10.                   פרשו את אצבעות שתי ידיכם.

בכדי לייצג את המכפלה 4X9.                                             

-  כל אצבע משמאל לאצבע המכופפת מייצגת כפולה של 10.(....10,20,30)
-  כל אצבע מימין לאצבע המכופפת מייצגת כפולה של 1.(....1,2,3)
-  בכדי למצוא את המכפלה 9X4 ספרו 31, 32, 33, 34, 35, 36.  

נערך לפי : http://www.multiplication.com/lesson10_nines_fingers.htm

א. נסו לכפול בשיטה זו כפולות שונות של המספר 9.
צפו גם בסרט " קל להכפיל ב-9 ", הסבירו והוכיחו באופן אלגברי מדוע השיטה עובדת.

Multiply By Nines Easy Math Trick

ב.  התוכלו להרחיב שיטה זו בכדי להכפיל מספרים דו ספרתיים (10-99) ב-9?

כיצד כופלים שני מספרים הגדולים מ-5 וקטנים מ-10 באמצעות האצבעות?

א. בימי הביניים הייתה נפוצה שיטה לכפל של מספרים בין 5-9 באמצעות האצבעות, 
    אשר הניחה ידיעת לוח הכפל עד מס' 5.
    צפו בסרט "כפל באצבעות" והתנסו בקסם שעומד מאחורי השיטה. 

ב. לפניכם דוגמא מתוך הסרט המסבירה כיצד כופלים 8X6 באמצעות האצבעות.
     הדגימו כפולות נוספות לפי שיטה זו.

           בכדי להכפיל 8X6:                                               פרסו את שתי ידכם, האגודל מייצגת את המספר 6, 
             כופפו ביד ימין                                                 האצבע 7 וכך הלאה עד הזרת שמייצגת את המספר 10.
אצבע אחת (6) וביד שמאל 3 אצבעות (8).                                                                                

ספרת האחדות של המכפלה היא: 2X4=8                               ספרת העשרות של המכפלה היא:   3+1=4 

              8X6=40+8=48  

ג. הסבירו והוכיחו באופן אלגברי מדוע השיטה עובדת

ד. הציעו שיטה לכפל בעזרת האצבעות למספרים בין 10 ל-15

ה. ליצור דמיוני שש אצבעות בכל אחת משתי ידיו. אילו כפולות הוא יוכל לבצע בשיטת כפל זו?

שיטות כפל וטריקים נוספים

  צפו בסרט הוידאו לשיטת הקווים, שיטה יעילה לכפל שני מספרים כלשהם.

הסבר על השיטה במאמר "כפל גוון וצבע" מתוך מספר חזק מס' 5.

שיטה נוספת לכפל שני מספרים כלשהם באמצעות הכפלה וחילוק ב-2 בלבד!

טריקים שונים ומדליקים לכפל בע"פ.  

תקציר| לקפל פרבולה 

הגדרה גיאומטרית:
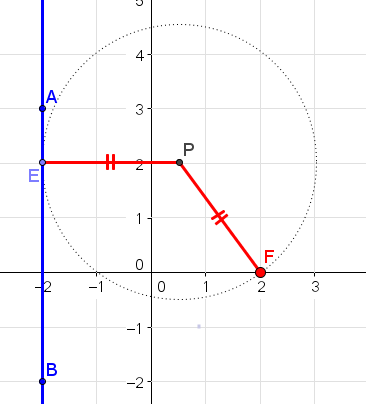
פרבולה היא המקום הגיאומטרי של כל הנקודות שמרחקן מנקודה קבועה (המוקד) וישר קבוע (המדריך) שווה.

1. בעזרת קיפולים של דף נייר ונקודה אחת עליו נוכל ליצור באורח פלא פרבולה.
ללא סרגל, מחוגה או כל כלי מדידה...

על דף נייר: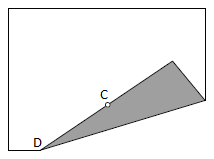 

-  סמנו נקודה C בקרבת אחת משפות הדף.
-  סמנו נקודה D על שפת הדף אליה התייחסתם קודם.
-  קפלו את הדף כך שהנקודה C תתלכד עם הנקודה D.
-  פתחו את הקפל וסמנו נקודה D אחרת על שפת הדף.
-  שוב קפלו את הדף כך שהנקודה C תתלכד עם הנקודה שסימנתם על שפת הדף.
-  חיזרו על התהליך עוד מספר פעמים.כדי לראות את התמונה שיוצרים הקפלים באופן ברור מומלץ לעבור עליהם בעזרת עפרון וסרגל.

מה קיבלתם?

- השוו את הנייר המקופל שלכם עם זה של חברכם. תארו את הדומה ואת השונה.

- קחו נייר נוסף, סמנו נקודה בתוכו במקום שונה וחזרו על התהליך. מה קיבלתם הפעם?

שאלות למחשבה:

א. ראינו כי הקיפולים יוצרים את המתאר של הפרבולה. מהם לדעתכם המוקד והמדריך?
ב. מה ניתן לומר על היחס הגיאומטרי בין הנקודות C,D וישר הקיפול ?
ג. מה ניתן לומר על ישר הקיפול ביחס לפרבולה ?
ד. אם נזיז את הנקודה C קרוב יותר לשפת הדף כיצד תשתנה הפרבולה? כיצד תשתנה הפרבולה אם נרחיק את הנקודה משפת הדף? 

 Thinking out loud 

2. לשחק בקיפולים:
בכדי להבין את הפלא ובכדי שנוכל לחקור מצבים שונים היעזרו ביישומון (קובץ גאוגברה להורדה).
א. גררו את הנקודה D והפעילו עקבות אחר הקיפולים. מה קיבלתם? מה ניתן לומר על כל קיפול ביחס לפרבולה? 
ב. בודאי שמתם לב כי הקיפול משיק לפרבולה, התוכלו לשער היכן נקודת ההשקה? כיצד נקודת ההשקה קשורה לנקודה D?
ג. צרו ביישומון פרבולות שונות על ידי שינוי מיקום הנקודה C.

1. כיצד תשתנה הפרבולה אם נמקם את C קרוב יותר לשפת הדף?
2. כיצד תשתנה הפרבולה אם נמקם את C רחוק יותר משפת הדף?
3. כיצד תשתנה הפרבולה אם נמקם את C על שפת הדף?
4. כיצד תשתנה הפרבולה אם נמקם את  C מתחת לשפת הדף?

3. כיצד נוכיח כי קיפולי הנייר יוצרים פרבולה?

נתבונן באיור הבא המייצג את קיפולי הנייר של הפרבולה: 

א. הסבירו מדוע CM=MD.
ב. הקו המקווקו מייצג את קו הקיפול. מה תוכלו לומר עליו ביחס ל- CD?
ג. נבנה אנך לישר המייצג את שפת הדף דרך הנקודה D. הסבירו מדוע CP=DP .
ד. הראו על פי ההגדרה הגיאומטרית של הפרבולה כי הנקודה P על הפרבולה.
ה. ציינו מיהו המדריך ומיהי נקודת המוקד.

4. עוד משחקי פרבולה

לפניכם יישומון לבניית הפרבולה כמקום הגיאומטרי.

א. הסבירו איזו תכונה מקיימת הנקודה P ביחס לישר המדריך ולנקודת המוקד.
ב. קרבו והרחיקו את נקודת המוקד מהמדריך. כיצד תשתנה הפרבולה?
ג. שנו את מיקום המדריך באופנים שונים. כיצד תשתנה הפרבולה?
ד. צרו, אם ניתן, בעזרת היישומון את הפרבולות הבאות: y²=-x, y=x² , y²=x+1
מצאו את המוקד והמדריך של כל פרבולה

נקודה למחשבה:
כיצד יראה המקום הגיאומטרי אם המדריך לא יהיה ישר אלא מעגל?

מקורות נוספים:

• הפרבולה כצורה גיאומטרית – חמוטל דוד, על"ה 29.
• Famous Curves Index– מדור באתר The MT History of Mathematics archive ובו רשימת עקומים מפורסמים במתמטיקה עם הסבר היסטורי ומתמטי וכן יישומים דינאמיים מדגימים.
• אוגדן למורה: גיאומטריה אנליטית - פעילויות ממוחשבות – מחשבמטיקה, מכון וייצמן

תקציר| מקומות גיאומטריים אנושיים| פתרונות

צאו החוצה אל החצר, רצוי ביום שמשי ונאה וגלו בהנאה מקומות גיאומטריים אנושיים. קחו עמכם גיר לשרטוט או כדור (לציון נקודה) וחבל (לציון ישר ואפשר גם למדידה) ורצוי גם מצלמה...

1. בחרו נציג מהכיתה שיעמוד במקום קבוע.

הסתדרו כך, שכל אחד מכם יעמוד במרחק 1 מטר ממנו.

באיזו צורה נעמדתם? הסבירו.

2. קבעו שתי נקודות במקום כלשהו. (שני כדורים או שתי אבנים).

הסתדרו כך, שכל אחד מכם יעמוד במרחק שווה משתי הנקודות.

באיזו צורה נעמדתם? מה מאפיין אותה ביחס לשתי הנקודות? הסבירו.

3. קבעו ישר על ידי מתיחת קו בגיר על הרצפה, או חבל.

הסתדרו כך, שכל אחד מכם יעמוד במרחק 1 מטר מהישר.

באיזו צורה נעמדתם? מה מאפיין אותה ביחס לישר? האם ישנן אפשרויות נוספות? הסבירו.

4. שרטטו בגיר זווית ישרה על הרצפה. (או בחרו פינה של מבנה).

הסתדרו כך, שכל אחד מכם יעמוד במרחק שווה משוקי הזווית.

באיזו צורה נעמדתם? מה מאפיין אותה ביחס לזווית? האם ישנן אפשרויות נוספות? הסבירו.

כיצד ישתנה המקום הגיאומטרי אם הזווית תהיה חדה? הסבירו.

5. קבעו ישר על ידי מתיחת קו בגיר על הרצפה, או חבל. קבעו נקודה.

הסתדרו כך, שכל אחד מכם יעמוד במרחק שווה מהישר וגם מהנקודה.

באיזו צורה נעמדתם? הסבירו. 

 Human Loci הפעילות מעובדת על רעיון מתוך inthinking.co.il

החתול והסולם המחליק

סולם נשען על עץ. החתלתולה טיפסה עד לגובה חצי מהסולם ואז הוא החל להחליק עד שהשתטח. החתלתולה נאחזה בסולם ולא הרפתה. התוכלו לדמיין מה המסלול שעשתה עם תנועת הסולם? 

היעזרו ביישומון.

nbsp;

א. מצאו את המקום הגיאומטרי המתאר את אוסף הנקודות בהן הייתה החתלתולה בשעה שהסולם החליק. הסבירו את התוצאה גם באופן גיאומטרי.

ב. אם החתולה היתה בגובה של שני שליש הסולם. מהו המקום הגיאומטרי שנוצר הפעם? 

החידה מעובדת לפי Numberplay: Catbird Seat - NYTimes.com 

מקורות נוספים:

 – פיצוח ובו שלושה כתבי חידה בהם רמזים למציאת שלושה מטמונים בעזרת מציאת המקום הגיאומטרי. כולל מעגל אפולוניוס. 
מחשבמתטיקה – פעילויות ממוחשבות (derive) בגיאומטריה אנליטית.

יישומונים דינאמיים

אריה, תנין והקוף - אנך אמצעי כאוסף הנקודות שמרחקן שווה משתי נקודות קבועות.
היכן המרכז? - מרכזי מעגלים המשיקים לשוקי זווית – חוצה זווית. יישומון מאת מתמטיקה משולבת, וייצמן. 
שאלה מבגרות - מתיחת מיתר במעגל, אליפסה ככווץ המעגל.  

תקציר| לרבע את הירח

אחת הבעיות שהעסיקו את המתמטיקאים מאות בשנים, היתה כיצד ניתן "לרבע" את המעגל, כלומר כיצד ניתן לבנות בעזרת סרגל ומחוגה ריבוע ששטחו כשטח מעגל נתון. בניסיונתיהם הרבים, ניסו גם לרבע צורות מעגליות כגון סהרונים.

"סהרון" היא צורה החסומה על ידי שתי קשתות מעגליות, בדומה לירח.    

1. לרבע את הסהרון של היפוקרטס

א. עקבו ביישומון אחר שלבי הבנייה ותארו במילים כיצד בנה היפוקרטס את הסהרון. רשמו את הנתונים באופן מתמטי.

ב. הראו כי שטח המעגל הקטן שווה לחצי משטח המעגל הגדול.              

ג. מה היחס בין שטח של הסהרון ושטח המשולש ?
חשבו את שטח הסהרון בעזרת חיבור וחיסור שטחים.

ד. בנו ריבוע ששטחו כשטח הסהרון.

2. לרבע את המעגל- האמנם?

היפוקרטוס טען כי "הוכיח" שניתן לרבע את המעגל, (לבנות ריבוע ששטחו שווה לשטח המעגל)

למרות שכיום ידוע שלא ניתן לעשות זאת. במה טעה היפוקרטס?


 

א. הראו כי :  שטח ששת הסהרונים - שטח המשושה = שטח המעגל הקטן היעזרו בחיבור וחיסור שטחים.

ב. משושה, בהיותו מצולע, ניתן לרבע, כלומר לבנות ריבוע בעל שטח שווה. היפורקטס הראה שניתן לרבע סהרונים.
מכאן ניתן להסיק שניתן לרבע את המעגל... האמנם? במה טעה היפורקטס?

3. לרבע את הסהרונים של אלחאסן

אלחאסן סרטט את שני סהרונים באיור הבא בעזרת שלושה חצאי מעגלים.

א. עקבו ביישומון אחר שלבי הבנייה ותארו במילים כיצד בנה את הסהרונים. רשמו את הנתונים באופן מתמטי.

ב. מה היחס בין שטח של שני הסהרונים ושטח המשולש ?

ג. בנו ריבוע ששטחו כשטח שני הסהרונים.

מקורות נוספים:

מי הפך את הירח לריבוע? – עטרה שריקי, קשר ח"ם

מצגת "לרבע את המעגל", רקע היסטורי ומתמטי. (באנגלית)

תקציר|  דלתוני ריצוף| לדפי גזירה| פתרונות והנחיות

1. פירוק והרכבה של משולש שווה-צלעות

לפניכם משולש שווה צלעות. כידוע גובה במשולש שווה-צלעות מחלק אותו לשני משולשים חופפים. (מדוע?)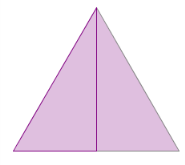  

גזרו משולש שווה צלעות והרכיבו מחדש את שני המשולשים על ידי הצמדת שני קדקודים של משולש אחד לשני קדקודים של המשולש השני.

כמה מצולעים שונים תוכלו להרכיב בדרך זו?

2. דלתון הריצוף

אחת הצורות שניתן ליצור באמצעות הצמדת המשולשים היא דלתון. 

דלתונים מיוחדים אלה נקראים דלתוני-ריצוף בגלל האפשרות ליצור

בעזרתם ריצופים של צורות גאומטריות רבות ואף של המישור כולו.

א. מהן התכונות המיוחדות של דלתונים אלה?

1. מהן מידות הזויות של דתלוני-ריצוף?
2. מצאו קשרים בין אורכי האלכסונים של הדלתון לבין אורכי הצלעות.

ב. גזרו מדפי הגזירה מספר דלתונים ונסו להרכיב באמצעותם מצולעים שונים, כך שדלתוני הריצוף נצמדים לאורך צלע שלמה.

1. אילו מהצורות הבאות ניתן להרכיב משולש, מרובע, מחומש, משושה?
2. אילו מצולעים משוכללים הצלחתם לבנות? הסבירו כיצד.

נסו להרכיב את המצולעים ביותר מאשר דרך אחת.

ג. הציעו דרכים שונות לרצף משטח בעזרת דלתוני הריצוף.

3. משושים

בבית הספר “חופים” יש חצרות פנימיות בצורת משושה. במסגרת פרוייקט לשיפור פני בית הספר עלתה הצעה
ליצור משטחים משושים באמצעות אריחי קרמיקה בצורת דלתוני ריצוף .

בקטלוג הגלריה לאריחים מצאו את הדגם שבתמונה וניסו לברר:

א. פי כמה גדול היקף המשושה החיצוני מהיקף המשושה הפנימי?
פי כמה גדול השטח?

ב. האם ניתן לבנות את ריצוף הקרמיקה באמצעות אריחים בשני צבעים בלבד, מבלי שלאריחים באותו צבע תהיה צלע משותפת?

ג. האם ניתן לבנות את ריצוף הקרמיקה באמצעות אריחים בשלושה צבעים בלבד מבלי שלאריחים באותו צבע תהיה צלע משותפת?

ד. האם ניתן להמשיך את הריצוף ולקבל משושה עוד יותר גדול הבנוי מאותם האריחים?
לכמה אריחים נוספים תזדקקו?

 4. ריצוף באריחים בשני גדלים

לפניכם שני אריחים לריצוף. שני דלתוני ריצוף כך שהצלע הקצרה בדלתון הגדול שווה באורכה לצלע הארוכה בדלתון הקטן.

א. מה יחס ההיקפים בין שני הדלתונים? מהו יחס השטחים?

ב. הצמידו את שני אריחי הדלתונים זה לזה. איזה מרובע התקבל? תארו תכונותיו.

ג. נסו להרכיב מצולעים שונים מדלתוני ריצוף אלו.

ד. האם ניתן לבנות דלתון ריצוף דומה גדול יותר המורכב משני אריחים אלו?

5. ריצוף באריחים בגדלים משתנים

תלמידי מגמת האמנות רוצים ליצור עיטור מיוחד לקיר מבנה המגמה בעזרת דלתוני ריצוף.
בהצעה ניתן להשתמש בגדלים שונים של דלתוני ריצוף.

התקבלו שתי הצעות:
הקבוצה של חן הציעה לבנות עיטור של פרח, והקבוצה של נוי הציעה לבנות עיטור משושה.

א. תארו את בניית הריצוף בכל אחת מההצעות.

ב. תכננו (בשרטוט או במילים) כיצד ניתן להוסיף שכבה נוספת לכל אחד מהעיטורים. לכמה דלתונים תזדקקו להוספת שכבה?

בעת שקילת ההצעה יש לבדוק בכל אחד מהעיטורים:

א. האם קיים יחס קבוע בין היקפי השכבות ?

ב. פי כמה גדול שטח האריחים הסגולים משטח האריחים בתכלת ?

ג. האם נוכל להגדיל את העיטור על ידי הוספת שכבות של דלתוני ריצוף?

ד. האם נוכל להוסיף שכבות נוספות של דלתוני ריצוף גם כלפי פנים?

ה. האם נוכל באופן זה למלא את כל השטח הלא מרוצף?

ו.  האם ניתן למלא את כל השטח הפנימי בדלתוני ריצוף בדרך אחרת?

קישורים 

דלתוני ריצוף בויקיפדיה

עוד ריצופי דלתונים בבלוג math humbre

היצירה Fractal Tessellation of Spirals שלהאמן Robert Fathauer מבוססת על דלתוני ריצוף

• טרנסיטיביות
• תורת המשחקים

תקציר | על מתמטיקה ודמוקרטיה| פתרונות

1. החלטה גורלית

בית ספר "עלומים" נקלע לקשיים כלכליים, וההנהלה נאלצה להודיע על קיצוצים בתקציב.

מועצת התלמידים המודאגת התגייסה כדי לסייע להחלץ מהמשבר, וכינסה את כל תלמידי השכבה הבוגרת לישיבת חירום

והציעה שלוש הצעות:

    א. לוותר על תקציב מסיבת סוף השנה ולגייס כספים באירוע התרמה לשכבה הצעירה.

    ב. קיצור הטיול השנתי  ביום ובמקומו לצאת ליום עבודה בחקלאות כתרומה לבית הספר.

    ג.  צמצום שירותי הנקיון בבית הספר ויצירת תורנות ניקיון של התלמידים.

לקראת ההצבעה, לאחר דיון סוער, יודעים כל המשתתפים בדיון את סדרי העדיפות של חבריהם.

יושב ראש מועצת התלמידים מתאר את התמונה הבאה:

- מרבית החברים מעדיפים את הצעה א על הצעה ב

- מרבית החברים מעדיפים את הצעה ב על הצעה ג

- מרבית החברים מעדיפים את הצעה ג על הצעה א.

האם מצב זה ייתכן? הסבירו.

2. בחירות למועצת תלמידים

בבית הספר "עלומים" מקיימים כל שנה בחירות למועצת התלמידים.

על פי חוקי בית הספר כל תלמיד יכול להציע את מועמדותו למועצת התלמידים. כל תלמיד שם בקלפי פתק עם שם אחד.

אם יש תלמיד שזכה ב- 40% מהקולות הכשרים או יותר , אז התלמיד שזכה במספר הקולות הגדול ביותר נבחר לראשות מועצת התלמידים.

אם אף אחד מהתלמידים לא זכה ב- 40% מהקולות הכשרים או יותר נערך סיבוב שני בו מתמודדים שני המועמדים שזכו במירב הקולות.

אלה מתן וגל מציגים את מועמדותם לראשות מועצת התלמידים.

    א. כמה אפשרויות לסדר עדיפות בין המועמדים קיימות?
 

    ב. לאחר חודש של תעמולת בחירות יודע כל אחד מתלמידי בית הספר את סדרי העדיפויות של כל אחד מחבריו:

96 תלמידים מחזיקים בסדר העדיפויות:  אלה  >  מתן  >  גל

110 תלמידים מחזיקים בסדר העדיפויות: מתן   >  גל    >  אלה

95 תלמידים מחזיקים בסדר העדיפויות: גל   >  אלה >  מתן

20 תלמידים מחזיקים בסדר העדיפויות: אלה  >  גל    >  מתן

20 תלמידים מחזיקים בסדר העדיפויות: מתן  >  אלה  >  גל

20 תלמידים מחזיקים בסדר העדיפויות: גל    > מתן    >  אלה

אם כל אחד יצביע על פי העדפותיו:  

  1. האם יהיה סיבוב בחירות שני?

  2. מי יהיה ראש מועצת התלמידים?


  3. המועמד מתן צופה את תוצאות הבחירות מראש. הוא וחברתו נועה מחליטים להצביע בעד גל (במקום בעד מתן).
 

האם החלטתם יכולה להשפיע על תוצאות הבחירות? הסבירו.

קישורים נוספים:

• דמוקרטיה מנקודת המבט של מתמטיקה– חומר לעבודות מחקר – ד"ר פיטר סמובול על שיטות בחירה שונות ופרדוקסים של בחירות.
• דמוקרטיה במספרים – שיעור באזרחות מאת מטח. עיבוד ניתוח של סקר המוצג בתמונות, אינפוגרפיקה. שימוש בתוכנת  Thinglink המאפשרת הוספת "נקודות חמות" על גבי תמונות.
• מקימים קואליציה (סימולציה) - הצעה לפעילות בכיתה בנושא הקמת הקואליציה בישראל בעקבות תוצאות הבחירות לכנסת ה-19. הפעילות מתבססת על סימולציה המבוססת על קובץ אקסל.
• בחירות רבותיי, בחירות – מכון דוידסון - בסדרת הכתבות נדבר על סקרי הבחירות, על ההסכמים שיוצר אחוז החסימה, על הקשר של הבחירות לתורת המשחקים ועוד.
• המתמטיקה של הדמוקרטיה – מאמר דיעה מתוך הבלוג – למה ללמוד מתמטיקה