כתב עת על"ה
מדורי המרכז
תקציר| 
הפסיכולוגיה של המבצעים |الحملة المربحة
מן העיתונות : הפסיכולוגיה של מבצעי הנחות
בכדי לעודד מכירות, ולפתות לקוחות לקנות מוצר מסוים, סוחרים יוצאים במבצע ומציעים אותו במחיר מוזל. אך למעשה הם מפסידים מכך. כך עולה ממחקר חדש שפורסם בכתב עת של שיווק (Journal of Marketing).
חוקרים , מאוניברסיטת מינסוטה בדקו את עמדות הצרכנים כלפי מדיניות הנחות. הם מצאו, שקונים מעדיפים לקבל תוספת חינם מאשר לקבל משהו זול יותר. הסיבה העיקרית לכך שרוב האנשים מתקשים בהבנת שברים ואחוזים. צרכנים מתקשים לעתים קרובות להבין , למשל, כי הגדלת הכמות ב- 50% שווה בערכה להנחה של 33% במחיר. הנחקרים העדיפו באופן גורף הגדלת הכמות על הוזלה במחיר. בניסוי, החוקרים מכרו 73% יותר קרם ידיים כשזה הוצע בחבילת בונוס מאשר כאשר הוצע במבצע הוזלה שווה ערך (גם לאחר שניטרלו השפעות אחרות, כגון הרצון לאגור) . תפיסה שגויה זו נשארה בעינה גם כשהמוצר היה בהנחה משמעותית. בניסוי אחר, הציעו שתי עסקות על מכירת פולי קפה : 33% כמות נוספת חינם או 33% הנחה על המחיר. הצעת ההנחה כדאית הרבה יותר, אך הקונים ראו את שתי ההצעות כשוות ערך.
מחקרים אף הראו דרכים אחרות שבהן סוחרים עלולים לנצל את חרדת המספרים של הצרכנים. אחת הוא לבלבל עם מבצעי הנחה כפולים. אנשים נוטים להעדיף מוצר שהופחת ב -20% , ולאחר מכן על ידי הנחה נוספת של 25% , יותר מאחד שהיה נתונה לשווה ערך, חד פעמי , הנחה של 40%.
1. קופסת דגנים של 500 גרם עולה 25 ש"ח.
המבצע הענק: קופסת הדגנים הוגדלה ב- 50% והמחיר נשאר 25 ש"ח.
המבצע החם: מחיר קופסת הדגנים הוזל ב- 50%.
איזה מבצע כדאי יותר לדעתך?
א. חשבו מה מחיר הדגנים ל-100 גרם.
ב. מה מחיר הדגנים ל-100 גרם במבצע הענק. (לאחר הגדלת הכמות) ?
ג. מהו אחוז ההנחה במבצע הענק של הגדלת הכמות ב- 50% ?
ד. מה מחיר קופסת הדגנים לאחר ההוזלה במבצע החם ?
מה מחיר הדגנים ל-100 גרם במבצע החם לאחר ההנחה?
ה. לאחר חישוביך – קבעו מהו המבצע המשתלם ונמקו.
ו. הציעו דרכים נוספות לפתרון.
2. קופסת מיץ תפוזים של 250 מ"ל עולה 5 ₪.
המבצע הענק: קופסת המיץ הוגדלה ב- 40% והמחיר נשאר 5 ש"ח.
המבצע החם: מחיר מיץ התפוזים הוזל ב- 25%.
איזה מבצע כדאי יותר לדעתך?
א. חשבו מה מחיר מיץ התפוזים לכל יחידת מ"ל בכל אחד מהמבצעים.
ב. מהו אחוז ההנחה במבצע הענק של הגדלת הכמות ב- 40% ?
ג. לאחר חישוביך – קבעו מהו המבצע המשתלם ונמקו.
3. חפיסת שוקולד של 100 גרם עולה 10 ש"ח.
המבצע הענק: חפיסת השוקולד הוגדלה ב- 50% והמחיר נשאר 10 ש"ח.
התבקשת ממנהל החנות לתכנן את המבצע כך שמחיר ההנחה במבצע הענק של הגדלת הכמות ב- 50% יהיה שווה ערך למחיר השוקולד במבצע החם.
באיזה אחוז יש להוזיל את חפיסת השוקולד?
4. חבילת עודיות של 200 גרם עולה 10 ש"ח.
מבצע פיצוץ: חבילת העוגיות הוזלה ב- 10%, ויום לאחר מכן הוזלה שוב ב- 30%.
מבצע חגיגה: חבילת העוגיות הוזלה ב- 40%.
איזה מבצע כדאי יותר לדעתך?
חשבו את מחיר חבילת העוגיות בכל אחד מהמבצעים.
לאחר חישוביך – קבעו מהו המבצע המשתלם ונמקו.
עובד ע"פ MatheMatics teacher | Vol. 107, No. 4 • November 2013
מקורות נוספים:
מבצעים חמים – אחוזים- יחידת לימוד בעריכת יעקב לדור, סמינר אורנים
תקציר| 
בדרך לפיתגורס| פתרונות| الطريق الى فيتاغوروس| حلول
1. עניין של דמיון
רשותך משולש ישר זווית אשר אורכי ניצביו 3 ס"מ ו-4 ס"מ.
יצרו שני משולשים חדשים באופן הבא:
הגדילו פעם אחת את המשולש פי 3.
הגדילו פעם נוספת את המשולש פי 4.
היעזרו ביישום הדינאמי ,
תוכלו להזיז ולסובב את המשולשים ולשנות את גודלם.
ב. ע"פ הדמיון שמצאתם חשבו את אורך היתר של המשולש המקורי ואת אורך היתר של המשולש החדש. התוכלו לנסח קשר ביניהם?
ג. באופן דומה חשבו את היתר של משולש ישר זווית אשר אורכי ניצביו 3 ס"מ ו- 7 ס"מ.
ד. בהינתן משולש ישר זווית בעל אורכי ניצבים: a ו-b . מה תוכלו לומר על אורך היתר ?
2. העפיפון
.יואב וחבורת הפיתגוראים בנו עפיפון המורכב משני משולשים ישרי זווית חופפים
א. הסבירו מדוע המקלות התומכים של העפיפון מאונכים זה לזה.
ב. יואב מצא שהמקל התומך הקצר מחלק את המקל התומך הארוך לשני חלקים באורך: 36 ס"מ ו- 64 ס"מ.
אך הוא וחבורתו התקשו לחשב את מידות העפיפון.
התוכלו לדעת מהן מידות העפיפון, כלומר לחשב את אורכי הניצבים של המשולשים?
תקציר| ערך מוחלט | ﻗﻴﻤﺔ ﻤطﻠﻘﺔ ﻓﻲ ﻤﻤر اﻟﺼﻔوف اﻟﺘﺎﺴﻌﺔ
בפעילות זו מומלץ להיעזר ביישומון "המסדרון", המדמה את ההליכה במסדרון והכיתות.
א. תארו במילים את השתנות המרחק של נעה מכיתה ט2 מהרגע שנכנסה למסדרון עד להגעתה.
ב. איך יראה לדעתכם גרף המתאר את השתנות המרחק של נעה מכיתה ט2 ביחס לזמן ההליכה שלה במסדרון? סרטטו איור המציג את הגרף הזה.
ג. צפו ביישומון אחר הליכתה של נעה במסדרון , ועצרו את הזמן עם הגעתה לט'2. הפעילו עקבות.
האם הגרף המתקבל תואם את השערכתם? הסבירו מה רואים בגרף?
ד. נעה הולכת מתחילת המסדרון עד ט'2. בנו פונקציה המתארת את המרחק של נעה ביחס לזמן הליכתה. מלאו את טבלת הערכים ובנו גרף מתאים. רשמו את התבנית האלגברית לפונקציה.
ה. בפעם אחרת נעה הולכת מתחילת המסדרון עד ט'2 , אבל אינה נעצרת וממשיכה מיד בדרכה עד ליציאה. תארו במילים את המרחק של נעה מהכיתה ט'2 מהרגע שנכנסה למסדרון עד ליציאתה מהמסדרון.
ו. איך יראה לדעתכם הפעם הגרף, המתאר את המרחק של נעה מכיתה ט'2 ביחס לזמן ההליכה שלה במסדרון? שרטטו גרף זה.
ז. צפו ביישומון ועקבו אחר הליכתה של נעה במסדרון , מכניסתה למסדרון עד ליציאתה. הפעילו עקבות. האם הגרף המתקבל תואם את השערכתם? הסבירו מה רואים בגרף?
ח. נעה הולכת מתחילת המסדרון עדסופו. בנו פונקציה המתארת את המרחק של נעה מכיתה ט2 ביחס לזמן. מלאו את טבלת הערכים ובנו גרף מתאים. רשמו את התבנית האלגברית לפונקציה.
(היעזרו בערך מוחלט)
ט. תלמידה אחרת, נטע מכיתה ט'4, גם צעדה מתחילת המסדרון עד לסופו. כיצד לדעתכם תשתנה הפונקציה והגרף, אם הפונקציה תתאר את המרחק שלה מ-ט'4.
י. שנו ביישומון את מספר הכיתה ל-4, וצפו אחר הליכתה של נטע במסדרון , מכניסתה למסדרון עד ליציאתה. הפעילו עקבות. האם הגרף המתקבל תואם את השערכתם? הסבירו מה רואים בגרף?
מה דומה ומה שונה בין שני הגרפים?
יא. ביום אחר נעה וגיל נכנסו למסדרון באותו זמן והלכו מתחילתו ועד סופו. גיל מיהרה מאד והלכה במהירות הכפולה מזו של נעה.במה יהיה שונה הגרף המתאר את מרחקה של גיל מט'2 לעומת הגרף המתאר את מרחקה של נעה מט'2?
יב. שוב במסדרון כיתה ט. נעה היתה בתחילת המסדרון וגיל היתה בקצהו השני. בדיוק באותו זמן, נעה וגיל הלכו זו לקראת זו באותה מהירות.
כיצד יראו הגרפים המתארים את מרחקה של נעה ושל גיל מט'2 ביחס לזמן?
מעובד על פי: MATHEMATICS TEACHER, 2012| Vol. 106, No. 3
הפעילות מתוך החוברת פונקציית ערך מוחלט לעתודה מדעית טכנולוגית.
פְרַקטָל הוא צורה גאומטרית שמורכבת מעותקים מוקטנים של עצמה בכל רמת פירוט שנסתכל בה.
לא חשוב כמה נתבונן אל תוך חלקיו של הפרקטל, תמיד נמצא בו חלקים הדומים לצורתו המקורית, כך שפרט קטן בצורה, דומה לצורת המקור כולה. (ויקיפדיה)
אחד הפרקטלים המפורסמים והמעניינים נקרא על שם מתמטיקאי פולני וולך סירפינסקי (1917), "שטיח סירפינסקי". הנה הוא לפניכם: התוכלו להסביר את מבנהו?
שישה שלבים בשטיח סירפנסקי מתוך: ויקיפדיה
לפניכם תיאור כיצד בונים את השטיח. מתחילים משטיח ריבועי שאורך צלעו 1 מטר. בסדרה של צעדים חותכים ממנו ריבועים קטנים יותר ויותר.
1. התבוננו באיורים, וביישומון. תארו במילים כיצד עוברים משלב לשלב.
2. השלימו את התמונה של השטיח בשלב השלישי. צבעו את הריבועים שחותכים מהשטיח.
3. כמה שטח ישאר מהשטיח בשלב ה-4? בשלב ה-5 ?
4. השלימו את טבלת הנתונים:
5. רשמו ביטוי אלגברי המתאר את הקשר בין מספר השלב בחיתוך השטיח לבין השטח שנותר.
6. כמה שטח ישאר בשלב החיתוך ה-10?
7. באיזה שלב של החיתוך יהיו יותר "חורים" מאשר שטח השטיח?
8. באיזה שלב של חיתוך ישאר מהשטיח רק 1% מהשטח המקורי?
9. מה תוכלו לומר על שטחו של שטיח סירפינסקי כאשר מספר החיתוכים שואף להיות אינסופי. 10. כיצד תשתנה הנוסחה של שטח השטיח החתוך אם נתחיל משטיח שאורך צלעו 4 מטרים.
למחשבה נוספת:
1. מהו ההיקף של השטיח לאחר חיתוך אחד? שימו לב להיקף גם סביב הריבוע הקטן שנחתך.
2. מהו ההיקף של השטיח בשלב השני, השלישי, הרביעי?
3. מה תוכלו לומר על ההיקף של שטיח סירפינסקי כאשר מספר החיתוכים שואף להיות אינסופי. 4. קראו על המימד של פרקטלים.
סרטונים מהרשת על פרקטלים:
מהו פרקטל – סרטון קצר המסביר את מבנה הפרקטל והופעותיו בטבע.
פרקטלים בעיצובים אפריקאים - הרצאה מרתקת מ-TED של רון אגלס.
מקורות נוספים:
מוזאון הכאוס הוירטואלי – מהו פרקטל? מהו המימד של הפרקטל?, סנונית.
משולש סירפינסקי –הוראות הכנה וחקירה – טומי דרייפוס, אוניברסיטת תל אביב.
משולש סירפינסקי – הוראות הכנה, כיתה בפיתה.
מה זה פרקטל? – אאוריקה.
משחקים כסביבה להצגת מושגים ומשפטים מתמטיים ולפתרון בעיות – נצה מובשוביץ הדר, על"ה 40
הפיצוח – אני דומה לעצמי
יום מעשים טובים - צל מרובעים
ביום המעשים הטובים שחל כל שנה ב-17.3.
מועצת התלמידים עורכת יריד קהילתי, בו התלמידים מציעים למכירה מוצרים שונים,
ונציגי הקהילה מציגים לתלמידים מגוון אפשרויות התנדבות בקהילה.
מועצת התלמידים חלקה תפקידים בארגון היריד.
1. צל מרובע ביריד
קרן ואורי התנדבו לתכנן ציליות ליריד. הם נדרשו להקצות לכל דוכן אותו שטח של צל.
הם הציעו לבנות את הצילייה באמצעים פשוטים של יריעת בד נמתחת וארבעה מוטות כמוצג באיור הבא.
קרן ואורי בנו דגם של צלייה, והצל שנוצר היה בצורת מרובע. מרובע הצל היה כללי, לא בעל כל תכונה מיוחדת.
כיצד יחשבו את הצל? קרן טענה שתוכל לחשב את שטחו, אם רק תוכל למקמו על רשת.
אורי, אשר היה ידוע בתחביבו של שרטוט מפות, נעזר במרצפות, ושרטט את המרובע על רשת.
משבצת אחת בשרטוט שווה ליחידת שטח.
א. הציעו דרכים שונות לחישוב את שטח המרובע.
ב. קרן ואורי החליטו לתכנן מרובעים שונים של צל באותו שטח. עזרו להם לתכנן במידה וניתן - ריבוע, מלבן, דלתון וכדומה באותו שטח נתון כאשר קודקודיהם על הרשת.
2. צללים מרובעים
שחר וטל הקימו דוכן כדי למכור לימונדה מפירות הגינה שלהם. הם הזמינו את הצילייה המוכנה הבאה בשטח של 25 יחידות שטח. אך ביום היריד נאלצו לשנות את אחד המוטות (אחד מקודקודי המרובע).
הזיזו רק את הנקודה P, כך ששטח המרובע PARK ישאר אותו דבר.
א. הציעו מרובעים שונים בשטח זהה.
ב. סמנו את הנקודות P המתאימות למרובעים שמצאתם. תארו כיצד מצאתם?
ג. מה משותף לכל הנקודות האלו ? כיצד תסבירו את התופעה ?
ד. תארו שיטה בה ניתן למצוא מרובע שווה שטח למרובע נתון.
ה. האם ניתן להזיז נקודה נוספת במרובע כך שהשטח ישמר ? מהי?
3. ללא כל צל של ספק או רשת
לפניכם מרובע PARK.
א. בנו מרובע ששניים מקדקודיו מתלכדים עם קדקודים של המרובע PARK ושטחו שווה לשטח המרובע PARK.
ב. בנו משולש ששניים מקדקודיו מתלכדים עם קדקודים של המרובע PARK ושטחו שווה לשטח המרובע PARK. (רמז – בנו מרובע שווה שטח ושנו אותו למשולש)
ג. בנו מחומש ששניים מקדקודיו מתלכדים עם קדקודים של המרובע PARK ושטחו שווה לשטח המרובע PARK.
ד. בנו מקבילית ששניים מקדקודיו מתלכדים עם קדקודים של המרובע PARK ושטחו שווה לשטח המרובע PARK.
האם הכדורגל הוא עגול? 
התבוננו בכדורגל.
מאילו מצולעים הוא מורכב? מה תוכלו לומר על תכונותיהם?
הכדורגל בנוי ממחומשים ומשושים משוכללים. גוף כזה נקרא פאון משוכלל למחצה. אך מהם הגופים המשוכללים? ומה מיוחד בהם? מהם גופים משוכללים למחצה?
ב. מהם גופים חצי משוכללים? ואיזה גוף הוא הכדורגל?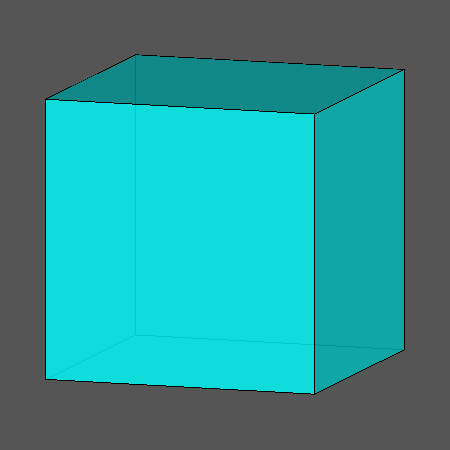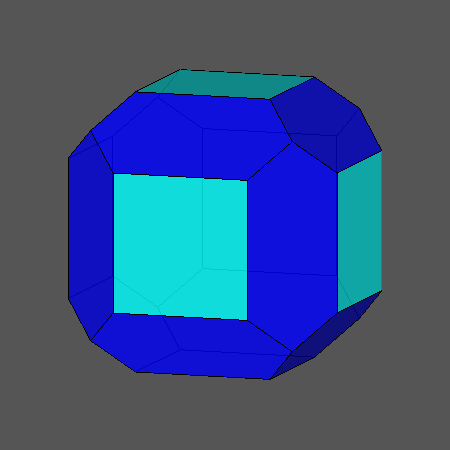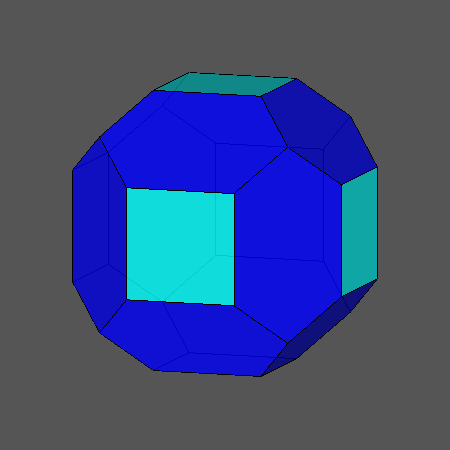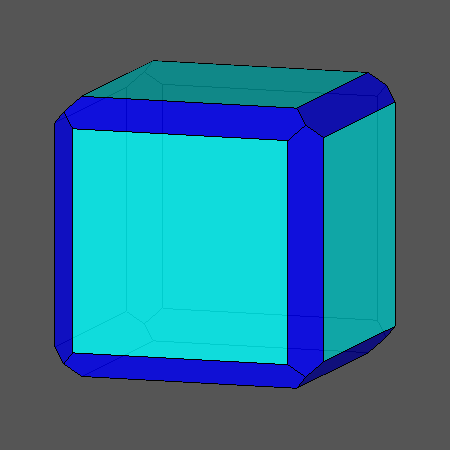
ג. האם גם אויילר שיחק בכדורגל?
ד. הכדורגל בחלל
