המרכז הארצי למורים למתמטיקה בחינוך העל יסודי

מדורי המרכז

pizza capture

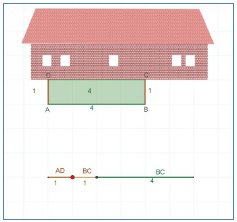
1. בפסטיבל מדברי גדול התמקמו שתי פיצריות במרחק 6 ק"מ זו מזו, והן מספקות על גמלים פיצות לכל דורש. הפיצריות זהות בתפריט, באיכות ובמחיר הפיצה, וכל אחת מהפיצריות גובה שקל אחד לק"מ דמי משלוח.

א. היכן תקנו את הפיצה (התייחסו למקומות שונים בהם אתם יכולים להימצא?

ב. היכן נמצא קו פרשת הפיצה – קו התפר בין האזור שבו עדיף לקנות מפיצרייה א לבין האזור בו עדיף לקנות מפיצרייה ב?

ג. תוכלו לחקור את הבעיה באמצעות היישומון היכן לקנות את הפיצה. קבעו את יחס המחירים בין הפיצריות ל- m=1. תוכלו להגדיל ולהקטין את המרחק מהפיצרייה השנייה ( $P_2$ ). כדי לראות היכן נמצאות כל נקודות החיתוך בין העגלים, השתמשו באופציה "הפעל עקבות".

2. כיצד ישתנה קו התפר בין אזורי השיווק של הפיצריות, אם פיצרייה א תמשיך לגבות 1 ₪ לק"מ דמי משלוח ואילו פיצרייה ב תעלה את דמי המשלוח ותגבה 2 ₪ לק"מ דמי משלוח?

כדי לחקור אפשרות זו שנו את היחס בין מחירי המשלוח ל- m=2. בהתאם ישתנה גם היחס בין הרדיוסים של המעגלים (מדוע?)

3. אתם מוכנים להמשיך ולחקור את הבעיה לכל בין דמי המשלוח, וכן למצוא את הפתרונות גם בדרך אלגברית. לנוחיותכם, וכדי שהפתרון שלכם יתאים ליישומון, מקמו את הפיצרייה המשנה מחירים בראשית הצירים, ואת הפיצריה הגובה שקל אחד לק"מ מקמו בנקודה (6,0).

תקציר|גלו את ההוכחה|חומר למורה

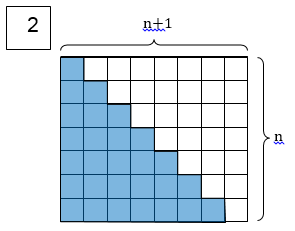
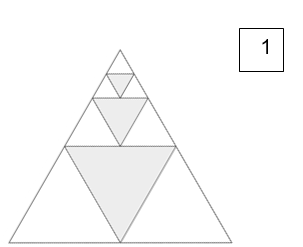
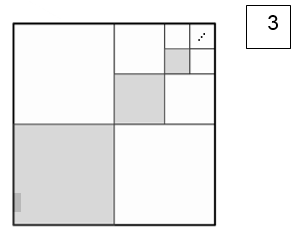
בכל אחד מן הסרטוטים מסתתרת הוכחה לנוסחה הקשורה לסכומי סדרות.

גלו את ההוכחה המסתתרת בכל סרטוט.

$\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\cdot \cdot \cdot =...$

$1+2+3+\cdot \cdot \cdot+n=$

$\frac{1}{4}+\frac{1}{16}+\frac{1}{64}+\cdot \cdot \cdot=...$

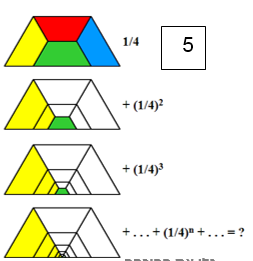בדיוק או בערך

בחרו את התשובה המדויקת ביותר בעיניכם

1. $\frac{1}{4}+\frac{1}{16}+\frac{1}{64}+\cdot \cdot \cdot=...$

א. $\frac{1}{3}$ . ב. קצת יותר מ- $\frac{1}{3}$ . ג. . קצת פחות מ- $\frac{1}{3}$ . ד. מתלבט/ת

2. $0.9+0.09+0.009+...=0.999...=$

א. 1. ב. קצת יותר מ- 1. ג. קצת פחות מ- 1 . ד. מתלבט/ת.

תקציר| pdf אופניים ואופנוע| pdf מדריך למורה

בעקבות מבחן מפמ"ר תשע"ז

bike and bicycle capture Q

א. באיזו מהירות רכב רוכב האופנוע?

ב. איזה מרחק עברו רוכב האופניים ורוכב האופנוע עד שנפגשו?

מה היחס בין המרחקים שעברו? האם אפשר היה לדעת זאת מראש?

ג. אופיר טוען שאפשר לחשב את המרחק שעבר רוכב האופניים בלי לדעת את המהירות, בלי להתייחס לכך שהרוכבים נפגשו כעבור 3 שעות, ובלי לפתור שום משוואה. כיצד לדעתכם עשה זאת?

ד. יובל אמר: הבנתי.

אם המרחק ביניהם היה 5 ק"מ. רוכב האופנוע היה רוכב 4 ק"מ ורוכב האופניים בדיוק קילומטר אחד עד לפגישה. האם יובל צודק? הסבירו.

ה. היישומון אופניים ואופנוע מציג את התנועה של רוכב האופניים ורוכב האופנוע כתלות בזמן. היישומון מאפשר לקבוע את מהירות הרכיבה של רוכב האופניים (מהירות הרכיבה של רוכב האופנוע נקבעת בהתאם), ומאפשר לקבוע את הזמן שחלף מתחילת הרכיבה.

הסבירו את דבריהם של אופיר ויובל באמצעות היישומון.

Q5 bike and bycicle

ו. הציעו שאלה נוספת הקשורה לנתונים שאפשר לענות עליה בלי לפתור משוואה.

תקציר| pdf מלבן ופרבולה| pdf מדריך למורה

בעקבות מבחן מפמ"ר תשע"ז

rectangle and parabula Q

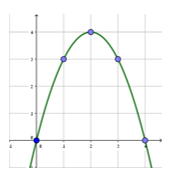
במערכת הצירים מסורטטים שני גרפים של פונקציות ריבועיות.
גרף אחד הוא של הפונקציה f(x) = x2 (מסומן ב-i ).

1. מי מבין הפונקציות הבאות לא יכולה להיות הפונקציה שהגרף שלה מסומן ב- ii? הסבירו. (יש יותר מאשר תשובה נכונה אחת)

rectangle and parabula capture (1) $g(x)=2x^2$

(2) $g(x)=x^2+4$

(3) $g(x)=3x^2$

(4) $g(x)=x^2-2$

(5) $g(x)=x^2+6$

(6) $g(x)=(x+2)^2$

2. נתון גם שהגרף המסומן ב- (ii) מתקבל מהגרף המסומן ב- (i) על ידי הזזה 4 יחידות למעלה.

א. מהם שיעורי נקודת הקדקוד של הפרבולה המסומנת ב- ii?

ב. כתבו את הביטוי האלגברי של הפרבולה המסומנת ((ii.

3. סרטטו מלבן שאחד מקדקודיו הוא ראשית הצירים וקדקוד נגדי לו הוא M(2,4). צלע אחת של המלבן על ציר ה- y (ראו סרטוט).

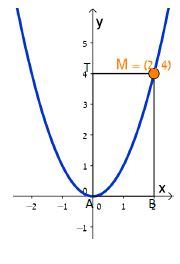
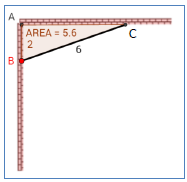
א. הסבירו מדוע נובע מהנתונים שלמלבן יש גם צלע המונחת על ציר ה- x.

ב. חשבו את שטח המלבן. הציגו דרך פתרון.

ג. איזו מבין המשוואות מתאימה לייצג את הישר
עליו מונח אחד מאלכסוני המלבן.

(1)y = 2x + 4 (2) y = –2x + 4
(3) y = x + 4 (4) y = –x + 4.

4. עדן בנתה (אפשר בעזרת היישומון) מלבנים נוספים ABMP, שאחד מקדקודיהם, M, נמצא על הפרבולה $y=x^2$ , ושני קדקודים שלהם על הצירים (ראו סרטוט).

bike and bicycle Q4

השלימו בטבלה מה שטח המלבן של כל אחד מהמלבנים שיצרה עדן.

		(3,__)	(2,4)	(1,1)	הנקודה M
			8 סמ"ר	1 סמ"ר	שטח המלבן

5. עדן שמה לב ששטח כל אחד מהם הוא $AB^3$ , כאשר $AB$ אורך הצלע המונחת על ציר ה- x. למשל: אם הקדקוד M הוא בנקודה (3,9), אורך הצלע $AB$ הוא 3 יחידות ושטח המלבן 27 יחידות. האם זה מקרי? הסבירו תוכלו להיעזר ביישומון.

6. עופר ואלון בנו מלבן שקדקוד אחד שלו על הפרבולה $y=x^2+4$ ,שתי צלעות שלו על הצירים ושתי צלעות מקבילות לצירים. הם סימנו ב- $x$ את הצלע המונחת על ציר ה- $x$ , וחיפשו ביטוי אלגברי לשטח המלבן כפונקציה של $x$ . עופר קיבל את הביטוי $x(x^2+4)$ , אלון קיבל את הביטוי $x^3+4x$ .

א. מי צודק? האם ייתכן ששניהם צודקים?

ב. כיצד חישב כל אחד מהם את שטח המלבן?

7. גם יעל בנתה מלבן עבור הפרבולה המוזזת $y=x^2+4$ , כאשר קדקוד אחד שלו על הפרבולה $y=x^2+4$ , שתי צלעות שלו על הצירים ושתי צלעות נוספות מקבילות לצירים. יעל חילקה אותו לשני מלבנים באופן שונה מאשר אלון.

סמנו ב- $x$ את הצלע המונחת על ציר ה- $x$ .

ניתן להיעזר ביישומון מלבן ופרבולה מוזזת.

א. הביעו בעזרת $x$ , את אורכי הצלעות של המלבן ABCD ואת שטחו.

ב. הביעו בעזרת $x$ , את אורכי הצלעות של המלבן PMCD ואת שטחו.

ג. הסבירו כיצד ניתן להביע את שטח המלבן של הפונקציה המוזזת ((ABCD כסכום שני מלבנים.

ד. האם קיים שוויון בין הביטויים שקיבלתם בסעיף א' לסעיף ג'? הסבירו שיקולכם.

תקציר|משולשים חסומים בפרבולה|מדריך למורה

triangle in parabola pic

פתחו את היישומון - משולשים החסומים בפרבולה, וענו על השאלות:

א. נתון גרף פונקציה ריבועית: $f(x)=-x^2+2x+8$

- מהן נקודות האפס של הפונקציה?

- מהו התחום בו הפונקציה אי שלילית?

- מהו ציר הסימטריה של הפרבולה?

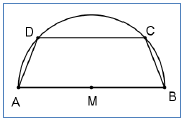
ב. חוסמים משולש בפרבולה בתחום בו היא אי שלילית.

עקבו ביישומון אחר בניית המשולש החסום בפרבולה באמצעות סרגל הנווט, (צעדים 1-7).

הסבירו במילים שלכם את הבניה.

ג. הזיזו את הנקודה K ועקבו אחר משולשים שונים החסומים בפרבולה.

האם לדעתכם קיים משולש בעל שטח מינימלי? בעל שטח מקסימלי?

ד. נסמן את שיעור ה-x של הנקודה K ב-x.

בטאו באמצעות x את שיעורי הנקודות M, L ,K ובדקו ביישומון בסרגל הנווט, (צעדים 7-11).

ה. דן הציג את שטחי המשולשים באמצעות פונקציית המטרה $s(x)=\frac{1}{2}(x-1)(-x^2+2x+8)$

גרף הפונקציה של דן מוצג ביישומון בחלון השמאלי (צעד 12).

הסבירו את הביטויים האלגבריים בפונקציה של דן.

ו. הזיזו שוב את הנקודה K שעל הפרבולה.

בחלון הימני מופיעה נקודה כתומה P, המתאימה ל-x את שטח המשולש החסום בפרבולה. כאשר תזיזו את הנקודה K, תוכלו לעקוב אחר השתנות שטח המשולש. במה דומה הגרף שיצרו העקבות לגרף הפונקציה שבנה דן ובמה הוא שונה ממנה?

ז. יצד תגדירו את פונקצית המטרה למציאת השטח המקסימלי של המשולש MLK? חקרו את הפונקציה ומצאו לה שתי נקודות מקסימום. מהם המשולשים המתאימים?

ח. הסבירו באופן גאומטרי מדוע קיימים שני משולשים בעלי שטח מקסימלי.

תקציר| מדריך למורה

אוסף פעילויות זה מציג מספר בעיות קיצון מתפתחות. האוסף בנוי כמספר רצפי פעילויות, מלוות ישומונים לחקר והמחשה.

הפעילויות מיועדות לתלמידים ומבוססות על פעילויות מהספר "ללמוד וללמד אנליזה", שיצא לאור בשיתוף פעולה של המחלקה לחינוך למדע וטכנולוגיה בטכניון, מנהלת מל"מ ומשרד החינוך.

רצף הפעילויות	מקום בתוכנית הלימודים	הפעילות	נושאים
פינת חי מלבנית	כיתה י'	חצר מלבנית	חקירת פונקצית פולינום. מתאימה כפעילות פתיחה.
		חצר פינתית	חקירת פונקצית פולינום
		חצר מחולקת	חקירת פונקצית פולינום, חקירת פונקציה עם פרמטר. (מתאים להצמחת הצורך בשימוש בפרמטרים)
		עניין של מחיר	חקירת פונקצית פולינום, חקירת פונקציה עם פרמטר.
פינת חי משולשת	כיתות י - י"א	חצר משולשת	פונקצית שורש מורכבת.
פינת חי משולשת	כיתות י - י"א	משולש ישר זווית החסום במעגל	חקירת פונקציות טריגונומטריות. אפשר לעקוף בדרך גאומטרית את השימוש בחקירת פונקציות טריגונומטריות.
עם הפנים לנוף	כיתות י - י"א		חקירת פונקצית פולינום, חקירת פונקציה עם פרמטר. מגבלות התחום.
החופש בחירת המשתנה החופשי	כיתות י - י"א		חקירת פונקציות שונות, חקירת פונקציה עם פרמטר. בחירת המשתנה החופשי חושפת תכונות מסויימות של התופעה. מערכים שונים לעבודה בקבוצות

תקציר| pdf עבודת שורשים| pdf מדריך למורה

בעקבות בחינת הבגרות לתלמידי 4 יחידות – 35481 – קיץ תשע"ו – מועד ב - שאלה 6

roots work original Question

חלק א

לפניכם גרף הפונקציה $h(x)=-x^{2}+4x+5$

1. מהו תחום ההגדרה של הפונקציה $f(x)=\sqrt{-x^{2}+4x+5}$ ?

2. מצאו את נקודות הקיצון המוחלט של הפונקציה f וקבעו את סוגן.

3. מה הקשר בין תחום העלייה של הפונקציה h לבין תחום העלייה של הפונקציה f? נסו להסביר את תשובתכם ביותר מאשר דרך אחת.

4. סרטטו באותה מערכת צירים את גרף הפונקציה $f(x)=\sqrt{-x^{2}+4x+5}$ .

היעזרו בנקודות המסומנות באדום. האם לכל אחת מהן יש נקודה מתאימה על גרף הפונקציה f?

5. על גרף הפונקציה h מסומנות בירוק שתי נקודות ששיעור ה- y שלהן הוא 1. הסבירו מדוע נקודות אלה נמצאו גם על גרף הפונקציה f?

(רמז: מה הקשר בין מספרים קטנים מ- 1 לבין השורשים הריבועיים שלהם?)

חלק ב

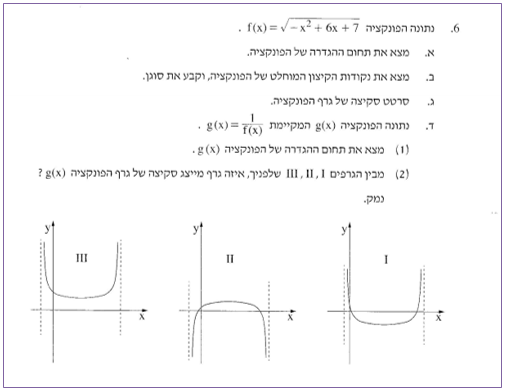
נתונה הפונקציה $g(x)=\frac{1}{\sqrt{-x^{2}+4x+5}}$

1.מהו תחום ההגדרה של הפונקציה g?

2. איזה מן הגרפים הבאים יכול לייצג סקיצה של גרף הפונקציה g? הסבירו.

roots work part B

חלק ג – סרטוט גרף של פונקציית שורש מורכבת בעזרת גרף הפונקציה הפנימית בלבד.

לפניכם גרף של פונקציה h.

נסרטט בעזרתו את גרף הפונקציה $f(x)=\sqrt{h(x)}$ : roots work part C

1. מהו תחום ההגדרה של הפונקציה f?

2. מצאו את נקודות הקיצון המוחלט של הפונקציה f וקבעו את סוגן.

4. סרטטו באותה מערכת צירים את גרף הפונקציה $f(x)=\sqrt{h(x)}$ . היעזרו בנקודות המסומנות.

חלק ד – הרחבת החקירה לפונקציות נוספות מהמשפחה $f(x)=\sqrt{h(x)}$ , כאשר h פונקציה ממעלה שנייה

היישומון שורשים מאפשר לסרטט גרפים של פונקציות שורש מורכבות, יחד עם פונקציה פנימית שהיא פונקציה ממעלה שנייה. משנים את הפרמטרים של הפונקציה הפנימית, והפונקציה המורכבת משתנה אף היא.

לנוחיות, נרשום את הפונקציה ממעלה שנייה בצורתה הקדקודית: $h(x)=a(x-m)^{2}+k$