תקציר| הפסיכולוגיה של המבצעים |الحملة المربحة 

מן העיתונות : הפסיכולוגיה של מבצעי הנחות

בכדי לעודד מכירות, ולפתות לקוחות לקנות מוצר מסוים, סוחרים יוצאים במבצע ומציעים אותו במחיר מוזל. אך למעשה הם מפסידים מכך. כך עולה ממחקר חדש שפורסם בכתב עת של שיווק (Journal of Marketing).

חוקרים , מאוניברסיטת מינסוטה בדקו את עמדות הצרכנים כלפי מדיניות הנחות. הם מצאו, שקונים מעדיפים לקבל תוספת חינם מאשר לקבל משהו זול יותר. הסיבה העיקרית לכך שרוב האנשים מתקשים בהבנת שברים ואחוזים. צרכנים מתקשים לעתים קרובות להבין , למשל, כי הגדלת הכמות ב- 50% שווה בערכה להנחה של 33% במחיר. הנחקרים העדיפו באופן גורף הגדלת הכמות על הוזלה במחיר. בניסוי, החוקרים מכרו 73% יותר קרם ידיים כשזה הוצע בחבילת בונוס מאשר כאשר הוצע במבצע הוזלה שווה ערך (גם לאחר שניטרלו השפעות אחרות, כגון הרצון לאגור) . תפיסה שגויה זו נשארה בעינה גם כשהמוצר היה בהנחה משמעותית. בניסוי אחר, הציעו שתי עסקות על מכירת פולי קפה : 33% כמות נוספת חינם או 33% הנחה על המחיר. הצעת ההנחה כדאית הרבה יותר, אך הקונים ראו את שתי ההצעות כשוות ערך.

מחקרים אף הראו דרכים אחרות שבהן סוחרים עלולים לנצל את חרדת המספרים של הצרכנים. אחת הוא לבלבל עם מבצעי הנחה כפולים. אנשים נוטים להעדיף מוצר שהופחת ב -20% , ולאחר מכן על ידי הנחה נוספת של 25% , יותר מאחד שהיה נתונה לשווה ערך, חד פעמי , הנחה של 40%.

1. קופסת דגנים של 500 גרם עולה 25 ש"ח.

המבצע הענק: קופסת הדגנים הוגדלה ב- 50% והמחיר נשאר 25 ש"ח.

המבצע החם: מחיר קופסת הדגנים הוזל ב- 50%.

 איזה מבצע כדאי יותר לדעתך?

       א. חשבו מה מחיר הדגנים ל-100 גרם.

       ב. מה מחיר הדגנים ל-100 גרם במבצע הענק. (לאחר הגדלת הכמות) ?

       ג. מהו אחוז ההנחה במבצע הענק של הגדלת הכמות ב- 50% ?

       ד. מה מחיר קופסת הדגנים לאחר ההוזלה במבצע החם ?
       מה מחיר הדגנים ל-100 גרם במבצע החם לאחר ההנחה?

       ה. לאחר חישוביך – קבעו מהו המבצע המשתלם ונמקו.

        ו. הציעו דרכים נוספות לפתרון.

2. קופסת מיץ תפוזים של  250 מ"ל עולה 5 ₪.

המבצע הענק: קופסת המיץ הוגדלה ב- 40% והמחיר נשאר 5 ש"ח.

המבצע החם: מחיר מיץ התפוזים הוזל ב- 25%.

איזה מבצע כדאי יותר לדעתך?

      א. חשבו מה מחיר מיץ התפוזים לכל יחידת מ"ל בכל אחד מהמבצעים.

      ב. מהו אחוז ההנחה במבצע הענק של הגדלת הכמות ב- 40% ?

      ג. לאחר חישוביך – קבעו מהו המבצע המשתלם ונמקו.

3. חפיסת שוקולד של 100 גרם עולה 10 ש"ח.

המבצע הענק: חפיסת השוקולד הוגדלה ב- 50% והמחיר נשאר 10 ש"ח.

התבקשת ממנהל החנות לתכנן את המבצע כך שמחיר ההנחה במבצע הענק של הגדלת הכמות ב- 50% יהיה שווה ערך למחיר השוקולד במבצע החם. 
באיזה אחוז יש להוזיל את חפיסת השוקולד?

4. חבילת עודיות של 200 גרם עולה 10 ש"ח.

מבצע פיצוץ: חבילת העוגיות הוזלה ב- 10%, ויום לאחר מכן הוזלה שוב ב- 30%.

מבצע חגיגה: חבילת העוגיות הוזלה ב- 40%.

איזה מבצע כדאי יותר לדעתך?

 חשבו את מחיר חבילת העוגיות בכל אחד מהמבצעים.
לאחר חישוביך – קבעו מהו המבצע המשתלם ונמקו.

עובד ע"פ MatheMatics teacher | Vol. 107, No. 4 • November 2013

מקורות נוספים:

משימות אוריינות בנושא אחוזים

מבצעים חמים – אחוזים- יחידת לימוד בעריכת יעקב לדור, סמינר אורנים

תקציר| בדרך לפיתגורס| פתרונות| الطريق الى فيتاغوروس| حلول

1. עניין של דמיון

רשותך משולש ישר זווית אשר אורכי ניצביו 3 ס"מ ו-4 ס"מ.

יצרו שני משולשים חדשים באופן הבא:

הגדילו פעם אחת את המשולש פי 3.

הגדילו פעם נוספת את המשולש פי 4. 

היעזרו ביישום הדינאמי , 
תוכלו להזיז ולסובב את המשולשים ולשנות את גודלם.

2. העפיפון

.יואב וחבורת הפיתגוראים בנו עפיפון המורכב משני משולשים ישרי זווית חופפים

א. הסבירו מדוע המקלות התומכים של העפיפון מאונכים זה לזה.

ב. יואב מצא שהמקל התומך הקצר מחלק את המקל התומך הארוך לשני חלקים באורך: 36 ס"מ ו- 64 ס"מ. 
אך הוא וחבורתו התקשו לחשב את מידות העפיפון.

התוכלו לדעת מהן מידות העפיפון, כלומר לחשב את אורכי הניצבים של המשולשים?

• אוריינות
• ערך מוחלט
• פונקציות

תקציר| ערך מוחלט | ﻗﻴﻤﺔ ﻤطﻠﻘﺔ ﻓﻲ ﻤﻤر اﻟﺼﻔوف اﻟﺘﺎﺴﻌﺔ 

בפעילות זו מומלץ להיעזר ביישומון "המסדרון", המדמה את ההליכה במסדרון והכיתות. 

א. תארו במילים את השתנות המרחק של נעה מכיתה ט2 מהרגע שנכנסה למסדרון עד להגעתה.

ב. איך יראה לדעתכם גרף המתאר את השתנות המרחק של נעה מכיתה ט2 ביחס לזמן ההליכה שלה במסדרון? סרטטו איור המציג את הגרף הזה.

ג. צפו ביישומון אחר הליכתה של נעה במסדרון , ועצרו את הזמן עם הגעתה לט'2. הפעילו עקבות. 
האם הגרף המתקבל תואם את השערכתם? הסבירו מה רואים בגרף?

ד. נעה הולכת מתחילת המסדרון עד ט'2. בנו פונקציה המתארת את המרחק של נעה ביחס לזמן הליכתה. מלאו את טבלת הערכים ובנו גרף מתאים. רשמו את התבנית האלגברית לפונקציה.

ה. בפעם אחרת נעה הולכת מתחילת המסדרון עד ט'2 , אבל אינה נעצרת וממשיכה מיד בדרכה עד ליציאה. תארו במילים את המרחק של נעה מהכיתה ט'2 מהרגע שנכנסה למסדרון עד ליציאתה מהמסדרון.

ו. איך יראה לדעתכם הפעם הגרף, המתאר את המרחק של נעה מכיתה ט'2 ביחס לזמן ההליכה שלה במסדרון? שרטטו גרף זה.

ז. צפו ביישומון ועקבו אחר הליכתה של נעה במסדרון , מכניסתה למסדרון עד ליציאתה. הפעילו עקבות. האם הגרף המתקבל תואם את השערכתם? הסבירו מה רואים בגרף?

ח. נעה הולכת מתחילת המסדרון עדסופו. בנו פונקציה המתארת את המרחק של נעה מכיתה ט2 ביחס לזמן. מלאו את טבלת הערכים ובנו גרף מתאים. רשמו את התבנית האלגברית לפונקציה.
(היעזרו בערך מוחלט)

ט. תלמידה אחרת, נטע מכיתה ט'4, גם צעדה מתחילת המסדרון עד לסופו. כיצד לדעתכם תשתנה הפונקציה והגרף, אם הפונקציה תתאר את המרחק שלה מ-ט'4.

י. שנו ביישומון את מספר הכיתה ל-4, וצפו אחר הליכתה של נטע במסדרון , מכניסתה למסדרון עד ליציאתה. הפעילו עקבות. האם הגרף המתקבל תואם את השערכתם? הסבירו מה רואים בגרף?
מה דומה ומה שונה בין שני הגרפים?

יא. ביום אחר נעה וגיל נכנסו למסדרון באותו זמן והלכו מתחילתו ועד סופו. גיל מיהרה מאד והלכה במהירות הכפולה מזו של נעה.במה יהיה שונה הגרף המתאר את מרחקה של גיל מט'2 לעומת הגרף המתאר את מרחקה של נעה מט'2?

יב. שוב במסדרון כיתה ט. נעה היתה בתחילת המסדרון וגיל היתה בקצהו השני. בדיוק באותו זמן, נעה וגיל הלכו זו לקראת זו באותה מהירות. 
כיצד יראו הגרפים המתארים את מרחקה של נעה ושל גיל מט'2 ביחס לזמן? 

מעובד על פי: MATHEMATICS TEACHER, 2012| Vol. 106, No. 3
הפעילות מתוך החוברת פונקציית ערך מוחלט לעתודה מדעית טכנולוגית.

תקציר|שטיח סירפינסקי| פתרונות 

פְרַקטָל הוא צורה גאומטרית שמורכבת מעותקים מוקטנים של עצמה בכל רמת פירוט שנסתכל בה.

לא חשוב כמה נתבונן אל תוך חלקיו של הפרקטל, תמיד נמצא בו חלקים הדומים לצורתו המקורית, כך שפרט קטן בצורה, דומה לצורת המקור כולה. (ויקיפדיה)

אחד הפרקטלים המפורסמים והמעניינים נקרא על שם מתמטיקאי פולני וולך סירפינסקי (1917), "שטיח סירפינסקי". הנה הוא לפניכם: התוכלו להסביר את מבנהו?

  שישה שלבים בשטיח סירפנסקי מתוך: ויקיפדיה

לפניכם תיאור כיצד בונים את השטיח. מתחילים משטיח ריבועי שאורך צלעו 1 מטר. בסדרה של צעדים חותכים ממנו ריבועים קטנים יותר ויותר.

1. התבוננו באיורים, וביישומון. תארו במילים כיצד עוברים משלב לשלב. 
2. השלימו את התמונה של השטיח בשלב השלישי. צבעו את הריבועים שחותכים מהשטיח.

3. כמה שטח ישאר מהשטיח בשלב ה-4? בשלב ה-5 ? 
4. השלימו את טבלת הנתונים:

5. רשמו ביטוי אלגברי המתאר את הקשר בין מספר השלב בחיתוך השטיח לבין השטח שנותר.
6. כמה שטח ישאר בשלב החיתוך ה-10?
7. באיזה שלב של החיתוך יהיו יותר "חורים" מאשר שטח השטיח? 
8. באיזה שלב של חיתוך ישאר מהשטיח רק 1% מהשטח המקורי?
9. מה תוכלו לומר על שטחו של שטיח סירפינסקי כאשר מספר החיתוכים שואף להיות אינסופי. 10. כיצד תשתנה הנוסחה של שטח השטיח החתוך אם נתחיל משטיח שאורך צלעו 4 מטרים.

למחשבה נוספת:
1. מהו ההיקף של השטיח לאחר חיתוך אחד? שימו לב להיקף גם סביב הריבוע הקטן שנחתך. 
2. מהו ההיקף של השטיח בשלב השני, השלישי, הרביעי? 
3. מה תוכלו לומר על ההיקף של שטיח סירפינסקי כאשר מספר החיתוכים שואף להיות אינסופי. 4. קראו על המימד של פרקטלים.

סרטונים מהרשת על פרקטלים:

מהו פרקטל – סרטון קצר המסביר את מבנה הפרקטל והופעותיו בטבע.

פרקטלים בעיצובים אפריקאים - הרצאה מרתקת מ-TED של רון אגלס. 

מקורות נוספים:

מוזאון הכאוס הוירטואלי – מהו פרקטל? מהו המימד של הפרקטל?, סנונית.

משולש סירפינסקי –הוראות הכנה וחקירה – טומי דרייפוס, אוניברסיטת תל אביב.

משולש סירפינסקי – הוראות הכנה, כיתה בפיתה.

מה זה פרקטל? – אאוריקה.

משחקים כסביבה להצגת מושגים ומשפטים מתמטיים ולפתרון בעיות – נצה מובשוביץ הדר, על"ה 40

הפיצוח – אני דומה לעצמי 

תקציר|יום מעשים טובים

יום מעשים טובים - צל מרובעים

ביום המעשים הטובים שחל כל שנה ב-17.3.

מועצת התלמידים עורכת יריד קהילתי, בו התלמידים מציעים למכירה מוצרים שונים,

ונציגי הקהילה מציגים לתלמידים מגוון אפשרויות התנדבות בקהילה.

מועצת התלמידים חלקה תפקידים בארגון היריד.

1. צל מרובע ביריד 

קרן ואורי התנדבו לתכנן ציליות ליריד. הם נדרשו להקצות לכל דוכן אותו שטח של צל.

הם הציעו לבנות את הצילייה באמצעים פשוטים של יריעת בד נמתחת וארבעה מוטות כמוצג באיור הבא.

קרן ואורי בנו דגם של צלייה, והצל שנוצר היה בצורת מרובע. מרובע הצל היה כללי, לא בעל כל תכונה מיוחדת.

כיצד יחשבו את הצל? קרן טענה שתוכל לחשב את שטחו, אם רק תוכל למקמו על רשת.

אורי, אשר היה ידוע בתחביבו של שרטוט מפות, נעזר במרצפות, ושרטט את המרובע על רשת.

משבצת אחת בשרטוט שווה ליחידת שטח.

א. הציעו דרכים שונות לחישוב את שטח המרובע. 
ב. קרן ואורי החליטו לתכנן מרובעים שונים של צל באותו שטח. עזרו להם לתכנן במידה וניתן - ריבוע, מלבן, דלתון וכדומה באותו שטח נתון כאשר קודקודיהם על הרשת.

 2. צללים מרובעים

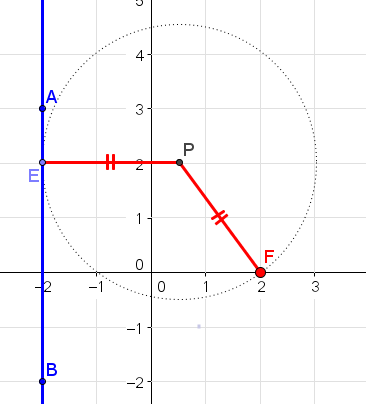
שחר וטל הקימו דוכן כדי למכור לימונדה מפירות הגינה שלהם. 
הם הזמינו את הצילייה המוכנה הבאה בשטח של 25 יחידות שטח. אך ביום היריד נאלצו לשנות את אחד המוטות (אחד מקודקודי המרובע).

א. הציעו מרובעים שונים בשטח זהה. 
ב. סמנו את הנקודות P המתאימות למרובעים שמצאתם. תארו כיצד מצאתם? 
ג. מה משותף לכל הנקודות האלו ? כיצד תסבירו את התופעה ? 
ד. תארו שיטה בה ניתן למצוא מרובע שווה שטח למרובע נתון. 
ה. האם ניתן להזיז נקודה נוספת במרובע כך שהשטח ישמר ? מהי?

3. ללא כל צל של ספק או רשת

לפניכם מרובע PARK.

א. בנו מרובע ששניים מקדקודיו מתלכדים עם קדקודים של המרובע PARK ושטחו שווה לשטח המרובע PARK.
ב. בנו משולש ששניים מקדקודיו מתלכדים עם קדקודים של המרובע PARK ושטחו שווה לשטח המרובע PARK. (רמז – בנו מרובע שווה שטח ושנו אותו למשולש) 
ג. בנו מחומש ששניים מקדקודיו מתלכדים עם קדקודים של המרובע PARK ושטחו שווה לשטח המרובע PARK. 
ד. בנו מקבילית ששניים מקדקודיו מתלכדים עם קדקודים של המרובע PARK ושטחו שווה לשטח המרובע PARK.

ה. הכדורגל במונדיאל

תקציר |  האם הכדורגל הוא עגול? |  בערבית

האם הכדורגל הוא עגול? 

תקציר

התבוננו בכדורגל. 
מאילו מצולעים הוא מורכב? מה תוכלו לומר על תכונותיהם?
הכדורגל בנוי ממחומשים ומשושים משוכללים. גוף כזה נקרא פאון משוכלל למחצה. אך מהם הגופים המשוכללים? ומה מיוחד בהם? מהם גופים משוכללים למחצה?

א. הגופים המשוכללים

ב. מהם גופים חצי משוכללים? ואיזה גוף הוא הכדורגל?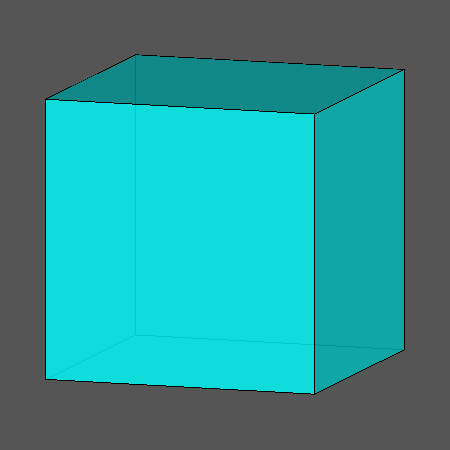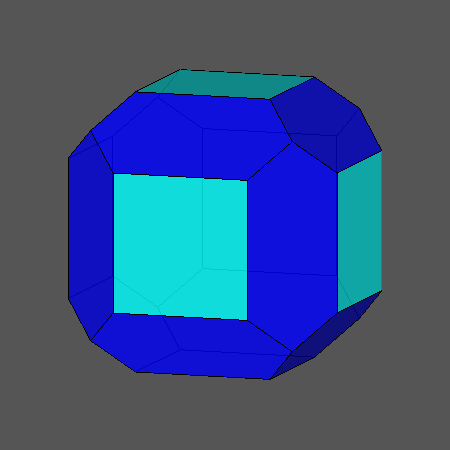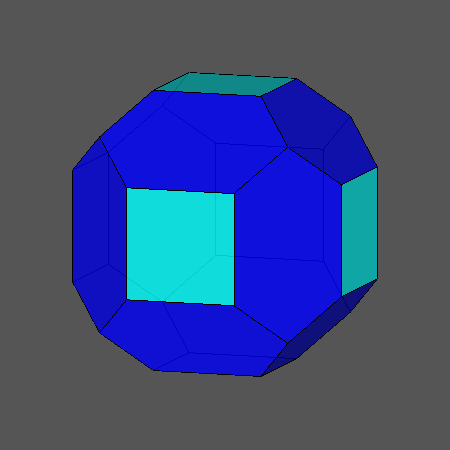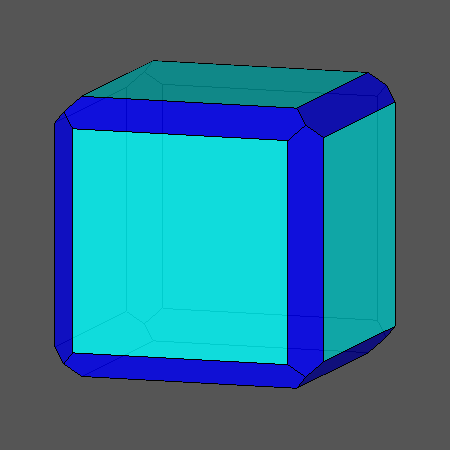

ג. האם גם אויילר שיחק בכדורגל?

ד. הכדורגל בחלל

ה. הכדורגל במונדיאל 

גלגלי המזל

תקציר| גלגלי המזל|  دواليب الحظ 

1. "גלגל אותה" פעילות אינטראקטיבית עם גלגל מזל, רולטה
2. בואו נתכנן גלגלי מזל
3. משחק התאמה בין גלגלי המזל וגרף העמודות- רמה קלה.
4. גלגלי המזל בעדלאידע - משחק התאמה בין גלגלי המזל וגרף העמודות - רמה בינונית
5. קישורים לפעילויות ומשחקים בנושא הסתברות

1."גלגל אותה"                                                                                                                     

במשחק "גלגל אותה" שני גלגלי מזל, הממוספרים מ- 1 עד 4. באפשרותכם לחבר או לחסר את שני המספרים. מספר המטרה שלכם הוא 3.

א. מהן כל האפשרויות לניצחון במשחק? כמה אפשרויות יש?

ב. מה לדעתכם הסיכוי לנצח במשחק? האם תבחרו בחיבור או בחיסור המספרים?

היישומון "גלגל המזל" – Nrich        

הדרכה 

ג. נסו את מזלכם בגלגל המזל.. סובבו ביישום האינטראקטיבי את שני גלגלי המזל וחברו את המספרים שהגרלתם.

     1. שחקו משחקון אחד, האם ניצחתם? שחקו 10 משחקונים, בכמה משחקונים ניצחתם? 
         הריצו את המשחק 100 משחקונים. בכמה משחקונים ניצחתם?

     2. איזה סכומים ניתן לקבל? איזה סכום הוא בעל הסיכוי הקטן ביותר להתקבל? 
         ואיזה סכום הוא בעל הסיכוי הגדול ביותר להתקבל?

     3. התבוננו בגרף העמודות, והסבירו מה מתארת כל עמודה.

     4. אם ניתנה לכם האפשרות לבחור במספר מטרה סכום לניצחון, איזה מספר הייתם בוחרים? 

ד. נסו שוב את מזלכם בגלגל המזל.. סובבו ביישום האינטראקטיבי את שני גלגלי המזל וחסרו את המספרים שהגרלתם.

     1. שחקו משחקון אחד, האם ניצחתם? שחקו 10 משחקונים, בכמה משחקונים ניצחתם? 
         הריצו את המשחק 100 משחקונים. בכמה משחקונים ניצחתם?

     2. איזה הפרשים ניתן לקבל? איזה הפרש הוא בעל הסיכוי הקטן ביותר להתקבל? 
         ואיזה הפרש הוא בעל הסיכוי הגדול ביותר להתקבל?

     3. התבוננו בגרף העמודות, והסבירו מה מתארת כל עמודה.

     4. אם ניתנה לכם האפשרות לבחור במספר מטרה הפרש לניצחון, איזה מספר הייתם בוחרים? 

מעובד על פי פעילות באתר Nrich

2. בואו נתכנן גלגלי מזל

א. בנו שני גלגלי מזל בהם הסיכוי לקבל סכום זוגי שווה לסיכוי לקבל סכום אי זוגי? הציעו זוגות שונים של גלגלי מזל.

ב. בנו שני גלגלי מזל בהם הסיכוי לקבל סכום זוגי גדול מהסיכוי לקבל סכום אי זוגי?

ג. בנו שני גלגלי מזל בהם הסיכוי לקבל הפרש זוגי שווה לסיכוי לקבל הפרש אי זוגי?

3. משחק התאמה

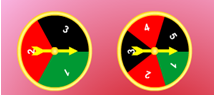
לפניכם שלושה זוגות של גלגלי מזל שיצרו את ארבעה גרפי עמודות. 
התאימו לכל זוג של גלגלי מזל את גרף העמודות המתאים לו. (שימו לב, האם מדובר בסכום או הפרש המספרים)

1. 

2. 

3.

4. גלגלי המזל בעדלאידע

ביריד העדלאידע יצרו זוגות שונים של גלגלי מזל מתוך הגלגלים מטה. באפשרותכם לבחור מתוכם זוג גלגלי מזל ולשחק את המשחק כאשר מספר המטרה הוא סכום המספרים שהגרלתם או הפרשם. אך גרפי העמודות השייכים לכל זוג התבלבלו... מי שייך למי?

5. קישורים

פעילויות נוספות

משחקי מזל בחנוכה – בפיצוח בעיות ברמות קושי שונות בהסתברות. בבעיה הראשונה משחק בו ניתן להתנסות עם יישום אינטראקטיבי.

פעילות בהסתברות וייצמן: זהירות 7 בדרך!: לתלמיד / למורה 

אי ודאות - משימות אוריינות, האגף לפיתוח תוכניות לימודים

מראשיתה של תורת ההסתברות – פרופ' אביטל , הסבר על מושג ההסתברות, ראשיתה של תורת ההסתברות בתקופת המתמטיקאים בליז פסקל ופייר פרמה ושימוש בה במשחקי מזל.

בעיה בהסתברות – והצעה לפתרונה באופן גרפי, גליונות לחשבון, פרופ' אביטל.

משחקים

סולמות ונחשים – שחקו בסולמות ונחשים, משחק אינטראקטיבי, עם גלגלי מזל (רמה 1) או שתי קוביות (רמה 2) וחקרו מה ההסתברות שלכם לטפס במעלה הלוח. הפעילות כוללת גם דפי עבודה , פתרונות ולוח משחק להדפסה. פעילות מאת Math Interactivities

משחקי מזל ביריד – משחק אינטרנטי (מותאם גם ל-IPAD) בו מספר שלבים. המטרה לזכות בכמה שיותר כרטיסים במשחקים בהם יש לחשב הסתברויות ברמות שונות. הכרטיסים יזכו אותך בכניסה ליריד בו עוד חמישה משחקי הסתברות שונים.

יישומונים להסתברות ניסויית

אוסף כלים אינטראקטיביים להגרלה – מטבע, קובייה, קלפים וגלגלי מזל. ניתן לבצע את ניסוי ההגרלה שוב ושוב ולראות את ההתאמה בין ההסתברות הניסויית להסתברות התיאורטית.

כלי אינטראקטיבי לבניית גלגל מזל צבעוני (הפעלת היישומון מומלץ להשתמש בדפדפן אקספלורר או להתקין בכרום את התוסף (החינמי)  (IE Tab

סרטונים בהסתברות

מהי ההסתברות למפולת שלגים? - סרטון ופעילות אינטראקטיבית לחקר ההבדל בין הסתברות ניסויית והסתברות תיאורטית והצגתן בגרף עמודות או טבלת שכיחות יחסית. מלווה בדף עבודה.

מהי ההסתברות למצוא דרכך במדבר? – סרטון אנימציה משעשע, תלת מימד, המסביר בפשטות והומור מושגי יסוד בהסתברות. 

 כפל בעזרת האצבעות- מטריקים בחשבון לאלגברה

תקציר|  כפל בעזרת האצבעות| פתרונות 

עוד משחר ההסיטוריה בני האדם משתמשים באצבעות הידיים לשם ספירה ופעולות חשבון.
בפעילות זו נכיר ונחקור כיצד אפשר לכפול בעזרת אצבעות הידיים.

כיצד כופלים ב-9 באמצעות האצבעות?

  כופפו את האצבע הרביעית                  אצבעותיכם מייצגות את המספרים 1 עד 10.                   פרשו את אצבעות שתי ידיכם.

בכדי לייצג את המכפלה 4X9.                                             

-  כל אצבע משמאל לאצבע המכופפת מייצגת כפולה של 10.(....10,20,30)
-  כל אצבע מימין לאצבע המכופפת מייצגת כפולה של 1.(....1,2,3)
-  בכדי למצוא את המכפלה 9X4 ספרו 31, 32, 33, 34, 35, 36.  

נערך לפי : http://www.multiplication.com/lesson10_nines_fingers.htm

א. נסו לכפול בשיטה זו כפולות שונות של המספר 9.
צפו גם בסרט " קל להכפיל ב-9 ", הסבירו והוכיחו באופן אלגברי מדוע השיטה עובדת.

Multiply By Nines Easy Math Trick

ב.  התוכלו להרחיב שיטה זו בכדי להכפיל מספרים דו ספרתיים (10-99) ב-9?

כיצד כופלים שני מספרים הגדולים מ-5 וקטנים מ-10 באמצעות האצבעות?

א. בימי הביניים הייתה נפוצה שיטה לכפל של מספרים בין 5-9 באמצעות האצבעות, 
    אשר הניחה ידיעת לוח הכפל עד מס' 5.
    צפו בסרט "כפל באצבעות" והתנסו בקסם שעומד מאחורי השיטה. 

ב. לפניכם דוגמא מתוך הסרט המסבירה כיצד כופלים 8X6 באמצעות האצבעות.
     הדגימו כפולות נוספות לפי שיטה זו.

           בכדי להכפיל 8X6:                                               פרסו את שתי ידכם, האגודל מייצגת את המספר 6, 
             כופפו ביד ימין                                                 האצבע 7 וכך הלאה עד הזרת שמייצגת את המספר 10.
אצבע אחת (6) וביד שמאל 3 אצבעות (8).                                                                                

ספרת האחדות של המכפלה היא: 2X4=8                               ספרת העשרות של המכפלה היא:   3+1=4 

              8X6=40+8=48  

ג. הסבירו והוכיחו באופן אלגברי מדוע השיטה עובדת

ד. הציעו שיטה לכפל בעזרת האצבעות למספרים בין 10 ל-15

ה. ליצור דמיוני שש אצבעות בכל אחת משתי ידיו. אילו כפולות הוא יוכל לבצע בשיטת כפל זו?

שיטות כפל וטריקים נוספים

  צפו בסרט הוידאו לשיטת הקווים, שיטה יעילה לכפל שני מספרים כלשהם.

הסבר על השיטה במאמר "כפל גוון וצבע" מתוך מספר חזק מס' 5.

שיטה נוספת לכפל שני מספרים כלשהם באמצעות הכפלה וחילוק ב-2 בלבד!

טריקים שונים ומדליקים לכפל בע"פ.  

תקציר| לקפל פרבולה 

הגדרה גיאומטרית:
פרבולה היא המקום הגיאומטרי של כל הנקודות שמרחקן מנקודה קבועה (המוקד) וישר קבוע (המדריך) שווה.

1. בעזרת קיפולים של דף נייר ונקודה אחת עליו נוכל ליצור באורח פלא פרבולה.
ללא סרגל, מחוגה או כל כלי מדידה...

על דף נייר: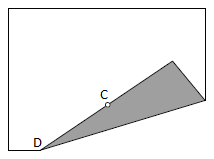 

-  סמנו נקודה C בקרבת אחת משפות הדף.
-  סמנו נקודה D על שפת הדף אליה התייחסתם קודם.
-  קפלו את הדף כך שהנקודה C תתלכד עם הנקודה D.
-  פתחו את הקפל וסמנו נקודה D אחרת על שפת הדף.
-  שוב קפלו את הדף כך שהנקודה C תתלכד עם הנקודה שסימנתם על שפת הדף.
-  חיזרו על התהליך עוד מספר פעמים.כדי לראות את התמונה שיוצרים הקפלים באופן ברור מומלץ לעבור עליהם בעזרת עפרון וסרגל.

מה קיבלתם?

- השוו את הנייר המקופל שלכם עם זה של חברכם. תארו את הדומה ואת השונה.

- קחו נייר נוסף, סמנו נקודה בתוכו במקום שונה וחזרו על התהליך. מה קיבלתם הפעם?

שאלות למחשבה:

א. ראינו כי הקיפולים יוצרים את המתאר של הפרבולה. מהם לדעתכם המוקד והמדריך?
ב. מה ניתן לומר על היחס הגיאומטרי בין הנקודות C,D וישר הקיפול ?
ג. מה ניתן לומר על ישר הקיפול ביחס לפרבולה ?
ד. אם נזיז את הנקודה C קרוב יותר לשפת הדף כיצד תשתנה הפרבולה? כיצד תשתנה הפרבולה אם נרחיק את הנקודה משפת הדף? 

 Thinking out loud 

2. לשחק בקיפולים:
בכדי להבין את הפלא ובכדי שנוכל לחקור מצבים שונים היעזרו ביישומון (קובץ גאוגברה להורדה).
א. גררו את הנקודה D והפעילו עקבות אחר הקיפולים. מה קיבלתם? מה ניתן לומר על כל קיפול ביחס לפרבולה? 
ב. בודאי שמתם לב כי הקיפול משיק לפרבולה, התוכלו לשער היכן נקודת ההשקה? כיצד נקודת ההשקה קשורה לנקודה D?
ג. צרו ביישומון פרבולות שונות על ידי שינוי מיקום הנקודה C.

1. כיצד תשתנה הפרבולה אם נמקם את C קרוב יותר לשפת הדף?
2. כיצד תשתנה הפרבולה אם נמקם את C רחוק יותר משפת הדף?
3. כיצד תשתנה הפרבולה אם נמקם את C על שפת הדף?
4. כיצד תשתנה הפרבולה אם נמקם את  C מתחת לשפת הדף?

3. כיצד נוכיח כי קיפולי הנייר יוצרים פרבולה?

נתבונן באיור הבא המייצג את קיפולי הנייר של הפרבולה: 

א. הסבירו מדוע CM=MD.
ב. הקו המקווקו מייצג את קו הקיפול. מה תוכלו לומר עליו ביחס ל- CD?
ג. נבנה אנך לישר המייצג את שפת הדף דרך הנקודה D. הסבירו מדוע CP=DP .
ד. הראו על פי ההגדרה הגיאומטרית של הפרבולה כי הנקודה P על הפרבולה.
ה. ציינו מיהו המדריך ומיהי נקודת המוקד.

4. עוד משחקי פרבולה

לפניכם יישומון לבניית הפרבולה כמקום הגיאומטרי.

א. הסבירו איזו תכונה מקיימת הנקודה P ביחס לישר המדריך ולנקודת המוקד.
ב. קרבו והרחיקו את נקודת המוקד מהמדריך. כיצד תשתנה הפרבולה?
ג. שנו את מיקום המדריך באופנים שונים. כיצד תשתנה הפרבולה?
ד. צרו, אם ניתן, בעזרת היישומון את הפרבולות הבאות: y²=-x, y=x² , y²=x+1
מצאו את המוקד והמדריך של כל פרבולה

נקודה למחשבה:
כיצד יראה המקום הגיאומטרי אם המדריך לא יהיה ישר אלא מעגל?

מקורות נוספים:

• הפרבולה כצורה גיאומטרית – חמוטל דוד, על"ה 29.
• Famous Curves Index– מדור באתר The MT History of Mathematics archive ובו רשימת עקומים מפורסמים במתמטיקה עם הסבר היסטורי ומתמטי וכן יישומים דינאמיים מדגימים.
• אוגדן למורה: גיאומטריה אנליטית - פעילויות ממוחשבות – מחשבמטיקה, מכון וייצמן