- עמוד הבית
- תקצירים כנס ארצי תשעז
- מושבים מקבילים- חלק ב'- כנס ארצי תשעח
- תוכנית הלימודים המוארת לחטיבת הביניים
תוכנית הלימודים המוארת לחטיבת הביניים
תיאור: הפעילות עוסקת בפתרון שאלות תנועה בדרך גרפית תוך שילוב בין הנושאים: פונקציה קווית, יחס, חפיפת משולשים ודמיון משולשים. הפעילות עוסקת בגרפים המתארים מרחק מנקודת יציאה כפונקציה של זמן. בגרפים אלה משמעות השיפוע היא מהירות. כשמדובר בשני גרפים במערכת צירים אחת מבחינים בין מקרים בהם מתוארת יציאה מאותו מקום בהפרש זמנים או יציאה ממקומות שונים באותו זמן או בהפרש זמנים. הפתרונות הנדרשים מבוססים על הבנה ולא על טכניקה אלגברית.
תיאור: הפעילות עוסקת בפונקציות קוויות וצורות גאומטריות שיוצרים הגרפים שלהן במערכת צירים. במסגרת ההוראה של הנושא 'פונקציה קווית' עוסקים בתכונות של הגרפים, כמו מקבילות או חיתוך בין ישרים. בהוראת התחום הגאומטרי עוסקים בחפיפת משולשים, דמיון משולשים, תכונות ומשפטים הקשורים במשולשים שווי שוקיים או משולשים ישרי זווית. השילוב בין התחומים מוצע בפעילות זו באמצעות קישור בין תכונות היסוד של מערכת צירים מאונכת, לבין תכונות גיאומטריות של מרובעים ומשולשים. התלמידים נדרשים להתייחס לתכונות של גרפים, לאפיין באמצעותם מרובעים ומשולשים, למצוא נקודות חיתוך של ישרים, ולחשב אורכים, יחס בין אורכים, שטחים והיקפים. בפעילות נדרש גם שימוש במשפט פיתגורס.
תיאור: המשימות בפעילות משלבות בין התחום האלגברי והתחום הגיאומטרי. בתחום האלגברי נדרשות מיומנויות הקשורות לתכונות הפונקציה הקווית ובתחום הגיאומטרי המשימות עוסקות בחפיפת משולשים, דמיון משולשים ותכונות של משולשים שווי שוקיים. השאלות מדורגות כך שבמעבר בין סעיפים יש עליה בדרגת החשיבה הנדרשת לצורך הפתרון. המשימות מתאימות לתלמידי כיתות ח' ברמות הגבוהות אך ניתן לעשות בהן שימוש גם בכיתה ט' כחזרה וריענון על הפרקים שנלמדו בכיתה ח'.
תיאור: מטרת הפעילות היא לפתח אצל התלמידים את ההתבוננות המבנית בביטויים אלגבריים ובמשוואות, במטרה לגלות בתוך התבניות מבנים חוזרים, המאפשרים לפשט ולקצר את העבודה, ולהכשיר את הקרקע ללימוד משוואות דו ריבועיות, משוואות טריגונומטריות, משוואות מעריכיות ועוד בחטיבה העליונה.
תיאור: פעילות זו נועדה לתרגל מיומנויות אלגבריות תוך כדי הפעלת תהליכי חשיבה לבחירת הפעולות הדרושות בכל משימה. הפעילות מתרגלת פירוק לגורמים ופתיחת סוגריים, ומחזקת את ההבנה שמדובר בפעולות הפוכות.
תיאור: מטרת הפעילות היא לחזק אצל התלמידים את המיומנות האלגברית בנושא פירוק לגורמים, ולהשתמש בפירוק לצמצום שברים אלגבריים ולפתרון משוואות בדרך קלה. התרגול כולל שימוש בכל ארבע השיטות של פירוק לגורמים: הוצאת גורם משותף, פירוק בעזרת נוסחאות הכפל המקוצר, פירוק לפי קבוצות, פירוק הטרינום.
תיאור: מטרת הפעילות היא לתרגל פירוק לגורמים לפי: זיהוי גורם משותף ונוסחאות כפל מקוצר. הפירוק ישמש לחישובים מהירים וקלים, הוכחת התחלקויות ופתרון בעיות.
תיאור: הפעילות שלפנינו מתרגלת ומחזקת את השימוש בנוסחאות הכפל המקוצר, תוך כדי התבוננות בתופעות מספריות יפות שהפענוח שלהן הוא בהישג ידם של תלמידים בכיתה ט'.
תיאור: אוסף משימות קצרות שמטרתן לחדד, להעמיק את ההבנה ולעורר שיח מתמטי בכיתה. המשימות מתאימות לתלמידי כיתה ט' ברמות הגבוהות. השאלות עוסקות בטכניקה אלגברית הקשורה לביטויים ריבועיים ולפונקציות ריבועיות ולייצוג הגרפי שלהן כפרבולות.
מקור: אתר הפייסבוק של עידן טל
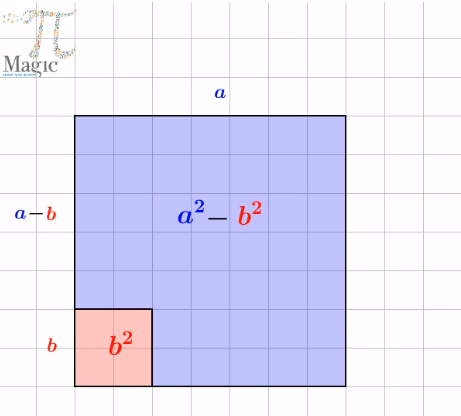
אופי הפעילות: תמונה דינאמית ממחישה ומעוררת דיון כיתתי
תיאור: התמונה הדינאמית מציגה משמעות גיאומטרית לנוסחה: (a^2-b^2=(a+b) (a-b
