- עמוד הבית
- תקצירים כנס ארצי תשעז
- מושבים מקבילים- חלק ב'- כנס ארצי תשעח
- תוכנית הלימודים המוארת לחטיבת הביניים
תוכנית הלימודים המוארת לחטיבת הביניים
מקור: nrich
אופי הפעילות: יישום דינאמי ובו סימולציה למכונת מספרים בה הקשר הוא לינארי.
תיאור: ניתן להכניס למכונה מספרים שונים, לצפות בתהליך החישוב ולנחש על פי התוצאות את הכלל לפיו עובדת המכונה. ביישום ניתן לחקור את הקשר לגרף הפונקציה ולטבלת המספרים. ניתן גם לבנות מכונות לפונקציות לינאריות שונות.
מקור: nrich
אופי הפעילות: יישומים דינאמיים לחקירת המצב ההדדי של ישרים: ישרים מקבילים , ישרים מאונכים , שיקוף של ישרים לציר ה-x ולציר ה-y.
תיאור: ביישום ישרים מקבילים עליכם להזיז את הנקודות כך שיתקיים התנאי שהישרים יקבילו ולחקור את הקשר של הישרים במשוואות האלגבריות שלהם.
מקור: nrich
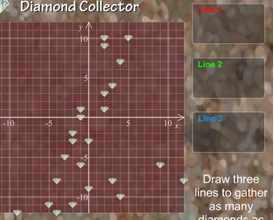
אופי הפעילות: משחק אינטראקטיבי מול המחשב או נגד חבר.
תיאור: האתגר הוא לחבר שלוש משוואות ישרים כך שיעברו דרך כמה שיותר נקודות בהן יהלומים.
מקור: Fun Based Learning
אופי הפעילות: משחק אינטראקטיבי לתרגול זיהוי ישרים ברמת מתחילים.
תיאור: יש להתאים משוואת ישר לנקודות נתונות במערכת הצירים. מטרתכם לאסוף כמה שיותר נקודות.
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
אופי הפעילות: יישום דינאמי לחקירת עליה וירידה של הישר.
תיאור: ביישום סימולציה של שני שטחים מלבניים, האחד מתמלא בצבע באופן קבוע והשני מתרוקן מצבע באופן קבוע. ניתן לעקוב אחר השתנות גובה הצבע בטבלאות המספריות, ובנקודות המתארות את גובה הצבע כפונקציה של הזמן. תוך האנימציה ניתן לראות בבירור את תהליך העליה והירידה ולחקור את הקשר לייצוג האלגברי.
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
אופי הפעילות: דף עבודה אינטראקטיבי בגאוגברה לחקירת השפעת הפרמטרים על משוואת הישר y=ax+b.
תיאור: כמו כן יש אפשרות לשרטט מדרגות שונות על פי שתי נקודות על הישר ולחקור את שיפוע הישר כיחס בין הפרש ה-y להפרש ה-x.
תיאור: אוסף תרגילים בנושא הפונקציה הקווית, המיועד לחזרה על כל המושגים הקשורים בה, כגון: משמעות השיפוע ומדרגות, מצבים הדדיים בין ישרים, נקודות חיתוך עם הצירים, מציאת משוואת של ישרים. המשימות מקשרות גם ליישומונים מבהירים.
תיאור: הפעילות נועדה לחזק את ההבנה של מושג השיפוע של פונקציה קווית דרך תיאור מקרה – סיפור. בסיפור: לקפיצים שונים מידת גמישות שונה. מידת הגמישות נלמדת באמצעות מדידות של אורכי הקפיצים בהתאם לכוח המופעל עליהם. כך ניתן לבנות גרפים על פי נקודות, בהן שיעור ה-X הוא מספר יחידות כוח שמופעלות על הקפיץ ושיעור ה-Y הוא אורך הקפיץ. מתוך המדידות השונות לומדים מהי מידת השינוי באורך הקפיץ בהפעלה של יחידת כוח אחת שהיא, למעשה, המספר המייצג את השיפוע.
תיאור: הפעילות עוסקת בהיבט האלגברי של מושג השיפוע של הפונקציה הקווית. מטרת הפעילות היא חיזוק המיומנות של השימוש במנת ההפרשים לחישוב השיפוע והבנת הקשר למושג: קצב שינוי. הפעילות מתחילה בבחינת השיפוע של פונקציה כלשהי ללא ביטוי מפורש. באופן זה מודגשת המשמעות של מנת ההפרשים.
תיאור: פעילות זו עוסקת בהבנת הקשר בין קצב השינוי של הפונקציה לבין השיפוע של גרף הפונקציה דרך סיפור מחיי היום-יום – תהליך הורדה של תוכנה מהאינטרנט (בהנחה שקצב ההורדה קבוע). הפונקציות המוצגות בפעילות הן פונקציות יורדות המתארות את גודל התוכנה שנותר להורדה (ב-MB) כפונקציה של הזמן שחלף מתחילת ההורדה. פעילות זו היא פעילות המשך לפעילות: "שיפוע של פונקציה קווית – מותחים קפיצים", העוסקת במשמעות השיפוע בהקשר של סיפור, עבור פונקציות עולות.
