- עמוד הבית
- מדורי המרכז
- פיצוחים
- גאומטריה
- דמיון
- תוכנית הלימודים המוארת לחטיבת הביניים
דמיון
מקור: מרכז מורים ארצי למתמטיקה בחינוך העל יסודי
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: דף עבודה ויישום דינאמי העוסק במשפט קטע אמצעים במשולש. דף העבודה מטפל בתכונות קטע אמצעים במשולש ובתנאים המספיקים וההכרחיים לקיומו.
מקור: Illuminations - NCTM
אופי הפעילות: חקירה אינטראקטיבית של מלבנים דומים , כיצד משתנה יחס הצלעות,יחס ההיקפים, ויחס השטחים . בפעילות נלווית ניתן גם לחקור את הגרפים של שינוי ההיקפים והשטחים במלבנים דומים. חקירה אינטראקטיבית של תיבות דומות , יחס המקצועות, שטחי פנים, הנפחים.
מקור: LearnZillion
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: סרטון ומצגת לשימוש בדמיון משולשים ישרי זווית לפתרון הבעיה – כיצד מוצאים את גובה הבניין. במצגת הסבר כללי על דמיון משולשים לפי זוויות, דוגמאות חישוביות והתייחסות לטעויות נפוצות. מצורף גם מדריך למורה.
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: דף עבודה אינטראקטיבי ובו בודקים מהו התנאי המספיק לדמיון משולשים והוכחתו.
תיאור: המשימות בפעילות עוסקות בגיאומטריה חישובית בהקשר של מצבים מחיי היום-יום. בפתרון המתמטי מודגש השימוש בדמיון משולשים, לצד שימוש במשפט פיתגורס, אחוזים ויחידות מידה. המשימות נכתבו בשתי גרסאות, כך שניתן להתאימן לתלמידים ברמה המצומצמת או לתלמידים ברמה הגבוהה יותר.
מקור: TED Ed
אופי הפעילות: סרטון מונפש ושיעור אינטראקטיבי
תאור: סרטון מונפש מביתTED Ed המספר את הרקע ההיסטורי והמתמטי של משפט פיתגורס, ומציג כמה מההוכחות היפות של משפט פיתגורס. הסרטון מלווה במדריך למורה, שאלון אינטראקטיבי, קישורים ועוד.
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: הפיצוח כולל שתי בעיות גיאומטריות במישור אשר ניתן להכלילן לגיאומטרית המרחב. הבעיה הראשונה מתאימה גם לתלמידי חט"ב ודורשת ידע בחישוב שטחים ונפחי פירמידה. הבעיה השניה דורשת שימוש במשפט פיתגורס ופתרון מערכת משוואות. הבעיות מזמנות חקירה ופיתוח ראיה מרחבית.
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
אופי הפעילות: יישום דינאמי בעריכת פרופ' יהודה שוורץ.
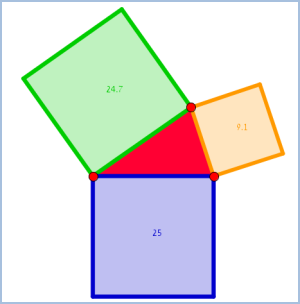
לפניכם משולש כלשהו, על צלעותיו בנויים ריבועים. מצאו קשרים שונים בין שטחי הריבועים הללו וקבעו באילו תנאים הם מתקיימים.
מקור: המרכז הארצי למורים למתמטיקה בחינוך העל יסודי
אופי הפעילות: בפעילות יישום דינאמי המציג הוכחה למשפט פיתגורס בעזרת פאזל שיצר פריגל. מומלץ שהתלמידים יגזרוע"פ ההנחיות ויבנו את הפאזל. היישום מדריך כיצד לבנות את הפאזל ומנחה כיצד להוכיח שבניית הפאזל אכן נכונה.
