- עמוד הבית
- מדורי המרכז
- פיצוחים
- במבט נוסף
- מדורי המרכז
- יישומים דינאמיים
אלגברה וחדו"א
נושא: פונקציה רציונאלית
כיתה: י-י"ב
תיאור: דף עבודה ויישום דינאמי לחקירה של אי רציפות של פונקציה רציונאלית.
- פרטים
- קטגוריה: פונקציה רציונאלית
נושא: משפחות של פונקציית חזקה. 
כיתה: י'
תיאור: דף עבודה ויישום דינאמי החוקרים את משפחת פונקציות החזקה בצורה המוזזת מהצורה f(x)=a(x-p)n+k .
ראשית יש חלוקה לפונקצית חזקה זוגית ואי זוגית.
לאחר מכן חוקרים הזזות ומתיחות של פונקציות החזקה.
פעילות זו היא הרחבה להכרות עם הפונקציה הריבועית בצורה הקודקודית.
- פרטים
- קטגוריה: פונקציות פולינום
נושא: פונקציה פולינומיאלית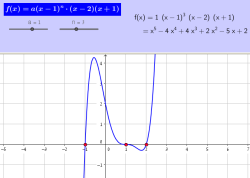 
כיתה: י-י"א
תיאור: דף עבודה אינטראקטיבי ויישום דינאמי בו ניתן לחקור כיצד משפיע
ריבוי השורש (חזקת הגורם) על התנהגות גרף הפולינום.
מבוסס על בחינת בגרות:
- פרטים
- קטגוריה: פונקציות פולינום
נושא: פונקציה פולינומיאלית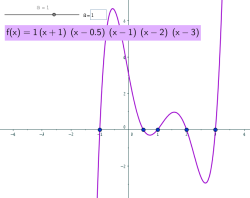
כיתה: י-י"א
תיאור: דף עבודה אינטראקטיבי ויישום דינאמי לחקירת הגרפים של פולינומים
המיוצגים כמכפלת גורמים לינאריים והשפעת ריבוי השורש על הגרף.
מבוסס על בחינת בגרות
- פרטים
- קטגוריה: פונקציות פולינום
נושא: קריאת גרפים
כיתה: ז - י
תיאור: דף עבודה אינטראקטיבי ויישום דינאמי לחקירת ההתאמה בין הפונקציה של שטחים בצורות שונות המתמלאים בצבע לפי הזמן, לבין הגרפים שלהם. ניתן לדון באופי השונה והדומה של קצב השתנות הפונקציות.
- פרטים
- קטגוריה: קריאת גרפים יישומים דינאמיים
נושא: קריאת גרפים.
כיתה: ז'- ח'
תיאור: יישום דינאמי ובו מוצגים שני כלים מלבניים, האחד ריק ומתמלא בצבע עם הזמן, והשני מלא ומתרוקן עם הזמן. ניתן לעקוב בטבלת הערכים, בנקודות מתאימות על הגרף ולהתאים לכל אחד מהם את הפונקציה ואת הגרף המתאים. ביישום מומחשת מאד התופעה של עליה וירידה של פונקציה בייצוגיה השונים.
- פרטים
- קטגוריה: קריאת גרפים יישומים דינאמיים
נושא: קריאת גרפים.
כיתה:
מבוסס על בחינת בגרות: המאגר החדש, שאלון 801, שאלה 21.
תיאור: דף עבודה ויישום דינאמי המבוססים על שאלה 21 בשאלון 801. ביישום מושם דגש על השיפועים השווים בגרף. יש אפשרות לשנות את השיפועים ולבדוק כיצד משתנה קצב גדילת השיער.
- פרטים
- קטגוריה: קריאת גרפים יישומים דינאמיים
נושא: שאלות קיצון.
כיתה: י- יא'
תיאור: יישום הדינאמי לחקירת שאלת קיצון מתוך שאלון בגרות ראשון, חרף 2016.
- פרטים
- קטגוריה: בעיות קיצון
נושא: שאלות קיצון.
כיתה: י- יא'
תיאור: יישום הדינאמי לחקירת שאלת קיצון מתוך שאלון בגרות ראשון, חרף 2017. היישום גם ממחיש את הקשר בין שטח המשולש ושטח האפור המשלים את הגזרה.
- פרטים
- קטגוריה: בעיות קיצון
נושא: בעיות קיצון
כיתה: י' -יב'
שאלון: בחינת הבגרות במתמטיקה שאלון שני ב-3 יח"ל, 35803 , קיץ תשע"ו.:שאלה 6
תיאור: המטרה העיקרית של הפעילות היא להדגיש שבבעיית ערך קיצון אנחנו מחפשים את הפתרון הטוב ביותר מבין כל הפתרונות האפשריים לבעיה.
הפעילות כוללת יישומון בגאוגברה, המאפשר לראות את מגוון האפשרויות לתכנן את הגינה, מציג את גרף הפונקציה המתאימה לארך צלע הריבוע את שטח הדשא, וממחיש את העובדה שהסרטוט הנתון בדף העבודה מתאר רק אפשרות אחת מתוך מגוון האפשרויות.
שני הסעיפים האחרונים הם הרחבה לשאלה. מתבוננים בפונקציה המתארת את סכום השטחים המיועדים לפרחים, ובודקים את הקשר בין שתי הפונקציות.
השאלה נבנתה עבור תלמידי 3 יח"ל אך בהחלט ניתן להתאימה לרמות גבוהות יותר בשלבים שונים של ההוראה.
- פרטים
- קטגוריה: בעיות קיצון
