יישומים דינאמיים
כיתה: י'- יב'
תיאור: דף עבודה אינטראקטיבי לחקירה של טרנספורמציות של היפרבולה. ניתן לחקור בעזרת היישום הדינאמי כיצד משפיעים הפרמטרים על גרף הפונקציה ועל מיקום האסימפטוטות האנכיות והאופקיות.
כמו כן ניתן לחקור את המעבר בין שני ייצוגים שקולים להיפרבולה.
הערה: ניתן להקדים את חקירת הנושא עוד לפני לימוד הנגזרות, כבר בכיתה י'.
נושא: משפחות של פונקציית חזקה. 
כיתה: י'
תיאור: דף עבודה ויישום דינאמי החוקרים את משפחת פונקציות החזקה בצורה המוזזת מהצורה f(x)=a(x-p)n+k .
ראשית יש חלוקה לפונקצית חזקה זוגית ואי זוגית.
לאחר מכן חוקרים הזזות ומתיחות של פונקציות החזקה.
פעילות זו היא הרחבה להכרות עם הפונקציה הריבועית בצורה הקודקודית.
נושא: פונקציה פולינומיאלית 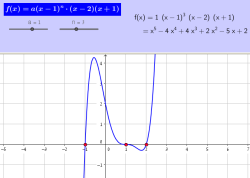
כיתה: י-י"א
תיאור: דף עבודה אינטראקטיבי ויישום דינאמי בו ניתן לחקור כיצד משפיע
ריבוי השורש (חזקת הגורם) על התנהגות גרף הפולינום.
מבוסס על בחינת בגרות:
נושא: פונקציה פולינומיאלית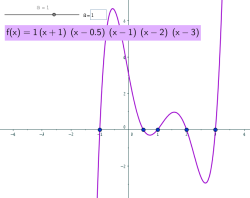
כיתה: י-י"א
תיאור: דף עבודה אינטראקטיבי ויישום דינאמי לחקירת הגרפים של פולינומים
המיוצגים כמכפלת גורמים לינאריים והשפעת ריבוי השורש על הגרף.
מבוסס על בחינת בגרות
כיתה: ז - י
תיאור: דף עבודה אינטראקטיבי ויישום דינאמי לחקירת ההתאמה בין הפונקציה של שטחים בצורות שונות המתמלאים בצבע לפי הזמן, לבין הגרפים שלהם. ניתן לדון באופי השונה והדומה של קצב השתנות הפונקציות.
כיתה: ז'- ח'
תיאור: יישום דינאמי ובו מוצגים שני כלים מלבניים, האחד ריק ומתמלא בצבע עם הזמן, והשני מלא ומתרוקן עם הזמן. ניתן לעקוב בטבלת הערכים, בנקודות מתאימות על הגרף ולהתאים לכל אחד מהם את הפונקציה ואת הגרף המתאים. ביישום מומחשת מאד התופעה של עליה וירידה של פונקציה בייצוגיה השונים.
כיתה:
מבוסס על בחינת בגרות: המאגר החדש, שאלון 801, שאלה 21.
תיאור: דף עבודה ויישום דינאמי המבוססים על שאלה 21 בשאלון 801. ביישום מושם דגש על השיפועים השווים בגרף. יש אפשרות לשנות את השיפועים ולבדוק כיצד משתנה קצב גדילת השיער.
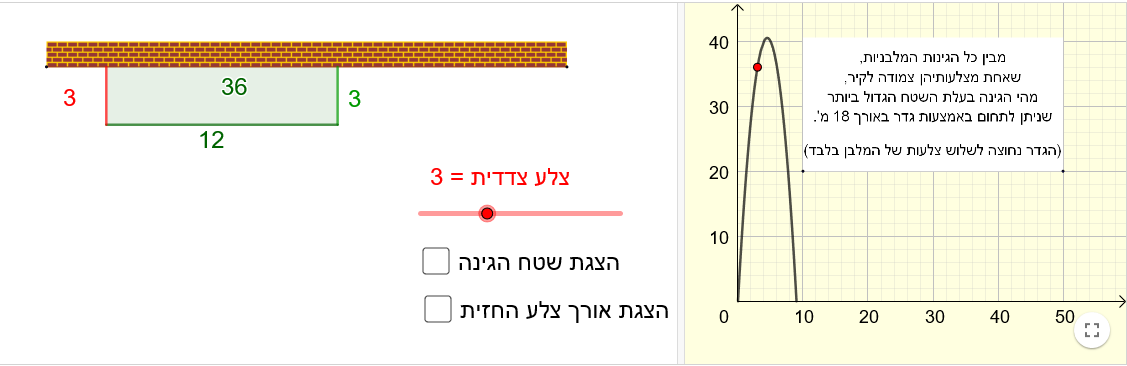
נושא: בעיות קיצון.
כיתה: ט
תיאור: היישומון מופיע בפעילות: למצוא את הפתרון הטוב ביתר – חלק ב. פעילות זו עוסקת במציאת מלבן בעל שטח גדול ביותר. היישומון מאפשר לעקוב אחר השתנות שטח הגינה כאשר משנים את צלעותיה.
כיתה: ט
תיאור: היישומון מופיע בפעילות: למצוא את הפתרון הטוב ביותר – חלק א העוסקת בבעיות ערך קיצון, אותן ניתן לפתור באמצעות מציאת קודקוד של פרבולה. הישומון מתאים לבעיה העוסקת בשטח של גינה. ניתן לעקוב אחר שינוי בשטח הגינה בצמוד לשינוי בגרף הפונקציה המתארת אותו.
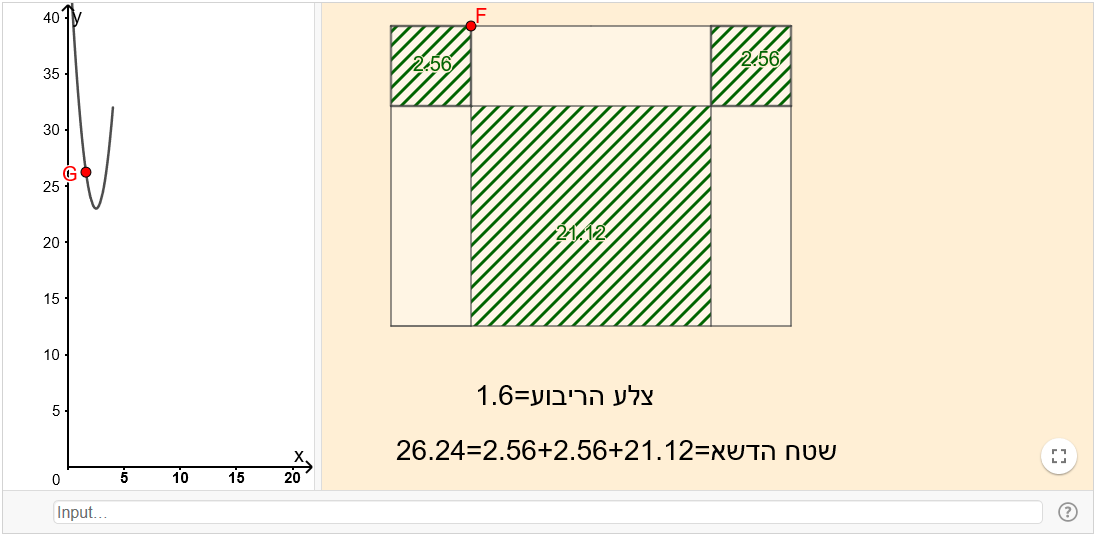
כיתה: ט
תיאור: הישומון מופיע בפעילות: למצוא את הפתרון הטוב ביותר – חלק א העוסקת בבעיות ערך קיצון, אותן ניתן לפתור באמצעות מציאת קודקוד של פרבולה. בישומון ניתן לעקוב אחר השינוי בשטח הרצפה בצמוד לשינוי בגרף הפונקציה המתארת אותו.