- עמוד הבית
- מדורי המרכז
- פיצוחים
- גאומטריה
גאומטריה
לקפל פרבולהכיתה: י"ב
תיאור: פעילות שבה ניצור פרבולה מקיפולי נייר, נחקור את השתנותה וננסה להבין מה המשמעויות הנלוות לכך.
פרויקט עולמי למדידת היקף כדור הארץ
כיתה: ז-י"ב
תיאור: בפיצוח הזמנה להשתתף בפרויקט בינלאומי למדידת היקף כדור הארץ באותן שיטות ועקרונות פשוטים ומדהימים
שהשתמש בהם ארטוסתנס לפני יותר מ-2000 שנה. ביום ה-22 בספטמבר,
תלמידים מרחבי העולם יבצעו את המדידה וישתפו זה את זה בתוצאותיהם.
בפיצוח הסבר על הפרויקט ואופן ביצועו וכן הסברים על שיטתו של ארטוסתנס הכוללים איורים וסרטים ממחישים.
הידע הבסיסי הנדרש לפעילות הוא מעט גיאומטריה.
כיתה: י-י"א
תיאור: הפיצוח עוסק בהוכחות ויזואליות של זהויות טריגונומטריות שונות כגון הנוסחאות לסכום זוויות ולזוויות כפולות.
בפיצוח משולבים יישומונים דינאמיים שניתן בעזרתם לחקור מצבים שונים ולהכליל.
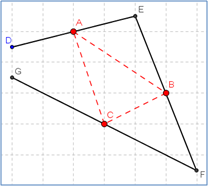מן הפנים אל החוץ
כיתה: ט-י
תאור: פיצוח, דף עבודה, יישום דינאמי - משולש לבעית חקר האם וכיצד ניתן לבנות משולש מנקודות אמצעי הצלעות. הבעיה גם מורחבת למרובעים וניתן לחקור בעזרתה יישום דינאמי - מרובע
כיתה: ז-ט'
תיאור: הפיצוח עוסק בגילוי תכונות גאומטריות של המשולש, הטרפז והמקבילית בעזרת קיפולי נייר.
הפעילות כוללת שימוש במושגים של קטע אמצעים במשולש ובטרפז, סכום זוויות במשולש ושטחים.
לסיום מובאת הצעה לחידה, פעילות חקר של משולש מצרי, בעל השלשה הפיתגורית המפורסמת 3:4:5.
נשמח לקבל פתרונות!
תודות ליפית אביטל שתרמה לנו מעבודתה.
בנוסף, לעיונכם: קיפולי נייר מתמטיים- אוסף קישורים למאמרים, פעילויות, אתרים ומצגות המוקדשים לאוריגמי ומתמטיקה.
כיתה: ז-י"ב
תיאור: הפיצוח עוסק בפיתוח הראיה המרחבית ומציאת חוקיות מעניינות תוך הסתכלות במשולשים שווי צלעות.
הבעיות בפיצוח דורשות להסתכל בצורה הגיאומטרית השלמה ובחלקיה,
למנות משולשים ולמצוא את החוקיות העומדת מאחורי המנייה ואף הכוונה להוכחת החוקיות באופן אלגברי.
הבעיות מדורגות בקושי ומתאימות לתלמידים החל מכיתה ז'. (לגילאי 9-99).
על כנפי הדמיון
כיתה: ט-י'
תיאור: אוסף בעיות בלתי שגרתיות, המתארות מבנה של גינה ציבורית, ופתרונן בעזרת דמיון משולשים. הבעיות מדורגות לפי רמת הקושי.
כיתה:
תיאור: פרופ' עמוס ארליך משתף אותנו בפעילות בנושא הוכחה. תלמידים מתלבטים כיצד להוכיח
שסכום הזויות במשולש הוא 1800 כאשר נתונה הנחת היסוד סכום הזוויות במרובע.
מן הפנים אל החוץ
כיתה: ט-י
תאור: פיצוח, דף עבודה, יישום דינאמי - משולש לבעית חקר האם וכיצד ניתן לבנות משולש מנקודות אמצעי הצלעות. הבעיה גם מורחבת למרובעים וניתן לחקור בעזרתה יישום דינאמי - מרובע
כיתה: ט'-י'
תיאור: בעיות ופעילויות שונות הנוגעות לטרפז. הפעילויות כוללות חקר יחסים שונים בתוך הטרפז,
הוכחה מקורית של משפט פיתגורס באמצעות טרפז, הוכחות שונות של נוסחת שטח הטרפז ולקינוח פרדוקס.
