תקציר|החיפוש אחר המספר המופלא e | פתרונות לשאלות העמקת הכרות עם המספר e |البحث عن العدد العجيب e|

אומרים על המספר e שהוא בן-דודו הצעיר של p  אשר לראשונה הופיע במאה ה-17.  

המתמטיקאי הצרפתי פורייה הראה בשנת 1815 כי המספר e, בדומה ל-p,הוא מספר אי רציונאלי (שלא ניתן להביעו כמנה של שני מספרים שלמים). 

ולא רק זאת,  בשנת 1874 הצליח הצרפתי הרמיט  להוכיח כי e, כמו בן דודו הקשיש p, הוא מספרטרנסצנדנטי, מספר לא אלגברי, כלומר, שאינו שורש של אף משוואה אלגברית בעלת מקדמים רציונאליים.    

הקירוב העשרוני ל-e  מתחיל כך : ...e = 2.71828182845904523536 

תוכלו לצפות בקירוב של e עד מליון ספרות אחרי הנקודה.                                                                                                                                                                                                                                                           

המספר e, הוצג לראשונה ע"י נפייר ( Napier) כאשר פיתח לוחות לוגריתמים.    

אך e נקרא בשמו, לזכרו של המתמטיקאי הדגול אוילר 

(Euler) מהמאה ה-18, שחקר רבות מתכונותיו הנפלאות.

מתמטיקאים רבים חיפשו קשר בין שני המספרים המופלאים p ו-e.
אחד הקירובים המדויקים להיום שייך לאיטלקי מישל פאנלי (Fanelli) והוא: אוילר אף הצליח לנסח קשר עם מספר מופלא נוסף i, בנוסחה היפהפייה .

e מופיע באופן מפתיע בהקשרים שונים ומגוונים במתמטיקה ויישומיה.

ניתן לפגוש אותו בכלכלה, פיסיקה, גיאומטריה, תורת המספרים, תורת ההסתברות ועוד.

מקורות: תבלינים מתמטיים- מחר 98, ספר המספרים- דייויד ויילס

הצעה לפעילות הכרות עם המספר e:

בפעילות נחקור כמה מההופעות של המספר e בשלושה היבטים שונים:

1. נוסחה של ריבית דה ריבית
2. סכום של סידרה אינסופית
3. בסיס של פונקציה מעריכית- חקירה בעזרת כלים ממוחשבים

הפעילות המוצעת היא לעבודה בכיתה בקבוצות (אפשר גם כשיעורי בית), בה כל קבוצה תגלה בעזרת דף העבודה את המספר המופלא e בדרך שונה. 

בסופה של החקירה תציג כל קבוצה בפני הכיתה כולה את המספר e שגילתה.

למתעניינים - עוד פיצוחים להעמקת ההכרות עם המספר e.

---

מקורות נוספים להרחבה והעמקה:

• סיפורו של המספר e - מאמר מאת אלי מאור בעל"ה 20
• e בראש הטור - עופר ליבה סוקר את ספרו של אלי מאור בעל"ה 17
• The Number e -  הצעה להכרות מקיפה עם המספר e בהופעותיו השונות.
• Imagining a Hit Thriller With Number e   אם היו עושים סרט על המספר e...

---

דף עבודה 1

ריבית דה-ריבית 

ברצוננו להשקיע שקל אחד בהשקעה הטובה ביותר.

כל הבנקים נותנים אותה ריבית שנתית של 6% אבל בתנאים שונים.

בנק א:  משלם את הריבית כעבור שנה, כך שבסוף השנה נקבל ___________ שקלים.

בנק ב:  משלם 3% כל חצי שנה, כך שבסוף השנה נקבל ________________ שקלים.

בנק ג:  משלם 1.5% כל רבע שנה, כך שבסוף השנה נקבל ______________ שקלים.

באיזה בנק תעדיפו להשקיע את השקל היקר שלכם?

בנק ד הציע לשלם את הריבית כל חודש בחודשו. מה הסכום שתקבלו בסוף השנה? ________.

באופן כללי, אם נשקיע שקל אחד בבנק המשלם ריבית שנתית של p%  המחושבת n פעמים בשנה, נקבל בסוף השנה:
________.

נניח שבנק מסוים היה מוכן לתת לנו עבור השקל, ריבית של 100%, והיה מסכים לחשב את הריבית מספר גדול מאד של פעמים בשנה, האם הבנק היה פושט את הרגל? 

האם ניתן לתאר את המספר e כשבר עשרוני סופי ? כשבר עשרוני מחזורי ?

מסקנה:   המספר e שווה בקירוב ל- __________ ושייך לקבוצת המספרים ה-__________

---

דף עבודה 2

סכום של סדרה אינסופית

הפרדוקס של זנון
אצן שרץ מנקודת ההתחלה A לנקודת היעד- B, לעולם לא יוכל להגיע למטרתו. 
לפני שיגיע לנקודה B הוא חייב להגיע לאמצע הדרך שבין A לבין, B ולפני שיגיע מאמצע הדרך 
לנקודה הסופית ,B הוא חייב להגיע לאמצע הדרך שבין נקודת האמצע לבין  Bוכך הלאה.

כלומר - הוא לעולם לא יוכל להגיע לנקודה B כי תמיד הוא יצטרך להגיע קודם לאמצע הדרך שבין 
נקודה B לבין הנקודה, שהוא נמצא בה 
זנון זרע את הרעיון של הגבול, הסכום האינסופי מתכנס לסכום סופי!

 

המספר e , על שם אויילר (Euler) שמצא שהוא הגבול של הסדרות הבאות: 

האם ניתן לתאר את המספר e כשבר עשרוני סופי ? כשבר עשרוני מחזורי ?

מסקנה:     המספר e שווה בקירוב ל- __________ ושייך לקבוצת המספרים ה-___________.

התוכלו לחשב?

 

---

דף עבודה 3

בסיס של פונקציה מעריכית- חקירה בעזרת כלים ממוחשבים

1. שרטטו בעזרת המחשב (ראו נספח) פונקציות שונות מהמשפחה y= ax . 

2. מצאו עבור כל פונקציה את שיפוע המשיק בנקודה בה x=0.

 

 

 

 

 

 מסקנה:

ככל שבסיס החזקה גדול יותר שיפוע המשיק בנקודה x=0 יותר__________.

 

 

נחפש פונקציה  y=ax, כזו ששיפוע המשיק שלה בנקודה בה x=0 הוא 1.

נסמן פונקציה זו :  ex

האם ניתן לתאר את המספר e כשבר עשרוני סופי ? כשבר עשרוני מחזורי?

 

 

 

 

מסקנה: המספר e שווה בקירוב ל- __________ ושייך לקבוצת המספרים ה-__________

---

נספח לשימוש בתוכנות מחשב לשרטוט גרפים

http://www.padowan.dk/graph- Graph 4.3:

תוכנה ידידותית לשרטוט וחקירה של גרפים. 

הוספת גרף חדש באמצעות הכפתור   מקבלים תיבת שיחה בה ניתן לרשום את נוסחת הפונקציה, קנה המידה ועיצוב צבע ועובי הגרף. התוכנה מאפשרת למצוא נקודות חיתוך עם הצירים ועם פונקציות אחרות, למצוא נקודות קיצון לחשב נגזרות ואינטגרלים ועוד. 

למשימתנו נשרטט משיקים לפונקציה בעזרת הכפתור  .

 http://www.geogebra.org/cms- GeoGebra

 

תוכנת מתמטיקה דינמית המאגדת גאומטריה, אלגברה ואנליזה. היא זכתה בפרסים בין-לאומיים כולל פרסי התוכנה החינוכית האירופי והגרמני. התוכנה ידידותית ונוחה ומלווה בתפריטים בעברית.

בשורת הקלט (למטה) רשמו את הפונקציה,  לדוגמה:   y = 2^x.

בכדי לשרטט את המשיק לפונקציה בחרו את הכפתור  סמנו את נקודת ההשקה ולאחריה את הפונקציה. 

הערה- ניתן להשתמש בפרמטרים באמצעות כפתור המחוון.  

 

תוכלו למצוא סקירה מקיפה יותר על שתי התוכנות בעל"ה 39 במאמר:

"שלוש תוכנות מתמטיות, כלי עבודה למורה ולתלמיד" מאת שרה גרז'וטיס.

---

עוד פיצוחים להעמקת ההכרות עם המספר e

1. במסיבת סוף השנה נערכה הגרלה גדולה בה 100 כרטיסים. 

ההסתברות של כל אחד מהכרטיסים לזכות בפרס זהה.

א. מה ההסתברות שהכרטיס שלך לא יזכה?

ב. מה ההסתברות ששני כרטיסים לא יזכו?

ג. מה ההסתברות שעשרה כרטיסים לא יזכו? 

ד. מה ההסתברות ש-100 כרטיסים לא יזכו? 

    חשבו מהו ההופכי להסתברות זו?

ה. אם במסיבה נמכרו n כרטיסי הגרלה.

    למה שואפת ההסתברות שאף אחד מבין n הכרטיסים יזכה, כאשר n שואף לאינסוף.

 

2. במשחק הקלפים הידוע "מלחמה" (במלעיל) כל שחקן קיבל חבילת קלפים. בכל תור חושף השחקן קלף מראש החבילה שלו. 

מצב של "מלחמה" קורה כאשר לשני השחקנים יש קלף זהה בדיוק (למשל, לשניהם אס יהלום אדום)

מהי ההסתברות שלא יהיה מצב של מלחמה במהלך משחק שלם (עד לחשיפת כל 52 הקלפים) ?

 

---

תקציר |  הפוך על הפוך | פתרונות | مقلوب على مقلوب

אם נתונה פונקציה חד-חד ערכית, (f(x, שבה לכל תמונה יש מקור אחד ויחיד, נוכל להפוך את ההתאמה ולהתאים לכל תמונה מקור. 
כך תתקבל פונקציה הפוכה (f ^-1(x. 
הקשר האלגברי בין התבניות המתאימות לשתי הפונקציות הוא שהמשתנים x ו- y התחלפו.

מבחינה גרפית, הגרפים של שתי פונקציות הפוכות זו לזו וסימטריים ביחס לישר y = x. כלומר, אם נקפל את מערכת הצירים לאורך הישר y = x, הגרפים של הפונקציות, יתלכדו. 

(ערוך לפי פונקציה הפוכה - יחידת לימוד משולבת מחשב של מכון וייצמן לכיתה ט'.) 

1. ניפגש או לא ניפגש?
   נקודות למחשבה...
   א. האם יתכן כי הגרפים של שתי פונקציות הפוכות לא יחתכו? תנו דוגמה.
   ב. ידוע כי לגרפים של שני פונקציות הפוכות ישנה נקודה משותפת אחת. כיצד תוכלו לאפיין אותה?
   ג. האם יתכן שלגרפים של שתי פונקציות הפוכות תהיינה שתי נקודות חיתוך ? אם כן, תנו דוגמה.
   ד. האם יתכן שלגרפים של שתי פונקציות הפוכות תהיינה יותר משתי נקודות חיתוך ? הסבירו.
   האם יתכן שהגרפים של שתי פונקציות הפוכות יתלכדו? נמקו.
   
   מתוך: אלה שמוקלר, זוגות של פונקציות, המחלקה להוראית הטכנלוגיה והמדעים, טכניון. 
   
2. הזוג הנצחי: הפונקציות המעריכית והלוגריתמית
   לפניכם גרפים של שתי פונקציות הפוכות, מעריכית ולוגריתמית בבסיס טבעי: y= lnx ,y=e^x
   אנו רואים כי הגרפים סימטריים ביחס לישר y=x ואין להם נקודה חיתוך. 
   
   
   
   
   
   
   
   
   
   
   נקודות למחשבה...
   א. האם יתכן ששתי פונקציות הפוכות, המעריכית (y=a^x ) והלוגריתמית, (y= log_a x) ישיקו זו לזו?
   אם כן, באיזו נקודה ועבור אילו ערכים של a?
   ב. האם יתכן שלשתי פונקציות הפוכות, המעריכית והלוגריתמית תהינה שתי נקודות חיתוך?
   שלוש נקודות חיתוך? אם כן, עבור אילו ערכים של a?
   ג. עבור אילו ערכים של לשתי הפונקציות אין כלל נקודות חיתוך?
   
   תוכלו להיעזר בסרטוט הגרפים של זוגות הפונקציות ההפוכות המעריכות-לוגריתמיות ובחנו את המצב ההדדי שלהם:
    
   לקריאה נוספת: עותמאן עלי, שתי הערות על נושאים מתוכנית הלימודים, על"ה 14, עמ' 42-53.
   
3. הקשר ההופכי
   האיור הבא מספר ללא מילים את הקשר בין נגזרת של פונקציה לנגזרת הפונקציה ההפוכה לה.
   התוכלו לנסח את הקשר ולהסבירו? 
   
   
   
   
   
   
   
   
   
   
   
   מתוך: "הוכחות ויזואליות ללא מילים" מאת א. זסלבסקי, ג. ויניצקי, קשר ח"ם.
   
   
4. נוסחה מהפכנית
   באחד מספרי הלימוד הישנים מצאנו נוסחה מעניינת ולצידה איור:
   
   התוכלו להסביר את הנוסחה ואת ייחודה?
   
   

   נקודות למחשבה...

   א. הביעו בעזרת אינטגרל מסוים את השטח הכחול.
   ב. הביעו את שטח המסגרת הצבעונית (הכחול והתכלת יחד).
   ג. הביעו את השטח הצבוע בתכלת בשתי דרכים שונות.
   ד. נגדיר: f(x)=x2. מצאו את ערכו של בשתי דרכים: בחישוב אינטגרל מסוים ובשימוש הנוסחה המהפכנית.
   ה. תוך שימוש בנוסחה המהפכנית, מצאו את ערכו של האינטגרל: 

מעובד לפי Nrich.maths.org

עוד על פונקציות הפוכות:

• זוגות של פונקציות - אלה שמוקלר - המחלקה להוראת הטכנולוגיה והמדעים, טכניון.
• פונקציה הפוכה - יחידת לימוד משולבת מחשב של מכון וייצמן לכיתה ט'.
• יחידה אינטראקטיבית על פונקציות הפוכות - באנגלית - של אוניברסיטת דיוק

פעילות מקוונת בנושא"משפט פיתגורס" 

מסע בעולם המרתק של רשת האינטרנט, תבקרו באתרים ממקומות שונים בעולם, העוסקים בפיתגורס האדם ופעלו לעולם המתמטיקה ותיישמו את משפט פיתגורס בבעיות שונות.

כתבה וערכה - נאווה מזרחי חט"ב "מיכה רייסר"- ראשון לציון

הרפתקאה פיתגורית

מאמר מבית "אלף אפס" המספר את סיפור מסע היתדות בן ה-3700 שנים על שלשת המספרים הידועה כשלשת פיתגורס.

כתבו: זיוה דויטש, עקיבא קדרי

משפט פיתגורס

מבחר הוכחות ללא מילים, מאמר של "אלף אפס".

ועוד חידות בנושא ויישומו.

 "כל דבר הוא מספר"

מאמר על תפיסותיו של פיתגורס את מושג המספר ואת המספרים הרציונאליים.

מאמר מאת "בארץ הדעת" כתב רועי יהושע.

תקציר|  משימה פרחונית | פתרונות |  مهمة مزهرة |  حلول

אורג שטיחים תכנן שטיחים בעיצוב של פרחים. בכדי להזמין צמר, היה עליו לחשב את כמות 
הצמר הלבן והצמר הצבעוני הדרושים לאריגת השטיח. התוכלו לעזור לו לחשב שטחים אלו?

1. בתוך ריבוע בעל צלע באורך 4 ס"מ, הוא צייר פרחים צבעוניים מארבעה חצאי מעגלים 
בשני אופנים שונים. חשבו עבור כל פרח, מהו השטח הצבעוני והשטח הלבן שנותר.

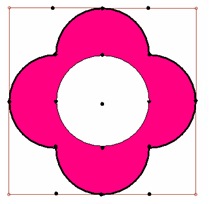
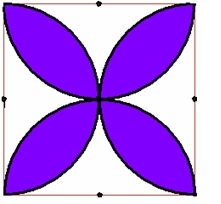
2. בתוך משושה משוכלל בעל צלע באורך 6 ס"מ, הוא צייר פרחים צבעוניים משישה חצאי 
מעגלים בשני אופנים שונים. חשבו עבור כל פרח, מהו השטח הצבעוני והשטח הלבן שנותר.

3. התבוננו בסרט הבא המציע עטיפה משושה ופרחונית לדיסק

8888888888888888888888888888

הציעו בניה של מעטפה דומה לכרטיס ברכה ריבועי.

בלינק הבא דוגמאות נוספות למעטפות ולקיפולי נייר אחרים:
http://www.instructables.com/id/Paper-Cd-Case-!!!-Flower-Design 

 4. הציעו דוגמאות נוספות לפרחים דומים וחישובי השטחים.

הידעתם?
פרח החיים הוא אחת הצורות בגיאומטריה המקודשת שחוצה תרבויות ויבשות, אולי הפרח טומן בחובו סוד, בנוסף להיותו צורה גיאומטרית יפה ומושלמת.
פרח החיים הוא תבנית גיאומטרית של עיגולים השזורים אלו באלו, מתוכם אפשר ליצור צורות גיאומטריות רבות נוספות. הוא התגלה בממצאים ארכיאולוגיים של תקופות עתיקות ביותר במקומות רבים ברחבי העולם.
קראו עוד על הפרח בעברית, באתר של Epoch Times Israel. 
קראו עוד בויקיפדיה.

הפעילות פותחה לפי רעיון מתוך: 
Mathamatics teacher, volume 98, no.9 May 2005 p617

תקציר|אוצרות פיתגורס|פתרונות|كنوز فيثاغورس|حلول

במצולות הים ליד האי סאמוס, מקום הולדתו של פיתגורס, נמצאו אוצרות בהם מטבעות עתיקים יקרי ערך. 

עזרו לחוקרים בחישוביהם למצוא את גודל המטבעות.

1. תיבת האוצר

בתיבה מלבנית שלושה מטבעות זהב הנוגעים זה בזה, בדומה לאיור (המטבע הגדול נוגע בשלוש צלעותיו של המלבן, הבינוני בשתי צלעותיו והקטן בצלע אחת).

רדיוס המטבע הקטן 4 ס"מ, רדיוס המטבע הבינוני 9 ס"מ. מה גודלו של המטבע הגדול?

2. מטבע הזהב

בגליל שקוטרו 2 ס"מ מונחים שלושה מטבעות בדומה לאיור. שני מטבעות ארד בקוטר 1 ס"מ המשיקים זה לזה ומטבע נוסף, מטבע זהב.

א. מהו גודל מטבע הזהב?

ב. מצאו מה המרחק בין מרכז מטבע הזהב למרכז הגליל.

ג. התוכלו למצוא באיור משולש 3:4:5?

3. ארד, כסף וזהב

שלושה מטבעות, הגדול מארד הבינוני מכסף והקטן מזהב, מונחים בקופסא מלבנית כך שהם משיקים לצלע המלבן ונוגעים זה בזה. רדיוס המטבע הגדול הוא 2 ס"מ ורדיוס המטבע הבינוני הוא 1 ס"מ.

א. מצאו מהו גודל מטבע הזהב.

ב. מצאו את מימדי הקופסא.

עובד על פי פעילויות מתוך: http://nrich.maths.org/

קישורים לבעיות נוספות ליישום משפט פיתגורס:

• מתוך "אלף אפס":
  - נתיב הזהב
  - אוסף בעיות על פיתגורס

• מתוך אתרו של דוד שי:  וריאציות פיתגוריות
• הפיצוח: משימה פרחונית
• Animated Pythagorean Theorem