- עמוד הבית
- פיצוחים
מעת לעת אנו שולחים פיצוח, פעילות מתמטית לכיתה, מכיתה ז' ועד יב.
כל הפיצוחים קשורים לתוכניות הלימודים בחט"ב ובחט"ע וניתן לשלבם במהלך ההוראה הן כחיזוק, העשרה והוראה בדרך אחרת.
אתם המורים והתלמידים, מוזמנים לשלוח פתרונות. ואת המיטב שבהם נדאג לפרסם.
זלילה גיאומטרית
תקציר| 
זלילה גיאומטרית| פתרונות| شراهة هندسية
1. פיצה "חצי חצי"
אורי ודנה הזמינו פיצה מלבנית וביקשו שחלקה תהיה עם זיתים וחלקה עם פטריות.
בפיצריה הציעו להם את החלוקות הבאות:
אורי ודנה התלבטו איזו חלוקה הוגנת יותר?
או בניסוח מתמטי, מהו יחס השטחים בכל אחד מהמלבנים, בין השטח הכחול והשטח הסגול?
2. עוגת יום ההולדת
אורי ודנה הכינו לאמם עוגת יום הולדת בתבנית ריבועית, וקישטו אותה בסוכריות צבעוניות (עם צבעי מאכל טבעיים בלבד) בצורה גיאומטרית מיוחדת.
הם חילקו את צלע העוגה הריבועית לשלשה חלקים שווים ויצרו ריבוע ושלושה טרפזים כמתואר באיור.
אמא, שהייתה בדיאטה, ביקשה את הריבוע הצהוב.
דנה ביקשה לעצמה את החלק הסגול עם הלבבות.
אורי ביקש את שני החלקים הכחולים עם הכוכבים.
איזה חלק מהעוגה קיבל כל אחד מהם?
כיצד ישתנה יחס השטחים כאשר אורך צלע הריבוע הצהוב הוא באורך כלשהו, לאו דווקא שליש צלע הריבוע החיצוני ?
3. לקינוח- שוקולד גיאומטרי
בשוקולד הגיאומטרי, בריבוע הפנימי מודפסת כבשה קטנה וחמודה.
חילקו את השוקולד הריבועי באופן הבא:
סימנו קטעים מאמצע של כל צלע הריבוע עד לאחד מהקודקודים של הריבוע שממול.
א. הוכיחו שהמרובע הפנימי הוא אכן ריבוע.
ב. מצאו מה היחס בין שטח הריבוע הפנימי לשטח הריבוע החיצוני.
ג. שאלה למחשבה-
כיצד ישתנה המרובע הפנימי כאשר נבחר נקודה כלשהי על צלע הריבוע (ולאו דווקא בחציה) וכיצד ישתנה אז יחס השטחים ?
חנוכה במספרים
1. סביבון מתמטי - סוב סוב סוב !
הסביבון המתמטי שלי מעושר, והוא נופל על אחד מהמספרים 1-10.
קיבלתי במתנה שלושה סביבונים מתמטיים שעל כל אחד מהם 10 מספרים, אך לא תוכלו לראותם.
סקרנים לדעת מהם המספרים?
סובבתי את כל אחד מהסביבונים המתמטיים 15 פעמים ורשמתי את כל המספרים שהתקבלו בעצירתם. הם כאן, לפניכם, בטבלאות מתאימות.
אחר-כך חזרתי על פעולה זאת פעמיים, אך הפעם שכחתי איזו טבלה מתאימה לאיזה סביבון.
לפניכם תוצאות הסיבובים ב- 6 טבלאות:
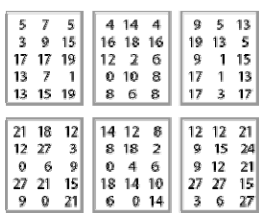
האם תוכלו לגלות מהי תכונת המספרים שעל כל אחד מהסביבונים הצבעוניים ולתת לכל אחד מהסביבונים המתמטיים שמות מתאימים?
2. סופגניות חמות ומתוקותאמא של אורי, בשם ועד ההורים, קנתה סופגניות חמות ומתוקות לכיבוד במסיבת חנוכה לכל בית הספר.
אורי והילה בקשו לקחת סופגניות לשכבה שלהם, אמא של אורי הסכימה, רק בתנאים שלה:
"קחו חצי מכל כמות הסופגניות ועוד חצי מסופגנייה אחת.
לאחר מכן, קחו רבע מכל הסופגניות שנותרו, ועוד רבע מסופגנייה אחת.
את מה שנותר תחזירו לי.
אך עליכם לשמור שכל סופגניות תשארנה שלמות."
אורי והילה לקחו את כל הסופגניות וכעבור שעה החזירו 50 סופגניות.
כמה סופגניות נקנו למסיבה וכיצד הצליחו אורי והילה לחלקן מבלי לפגום בשלמותן?
מעובד מתוך: על כנפי האגדה, הטכניון, פרויקט "מחר 98"
3. הנרות הללו
דורון הוציא מקופסת נרות החנוכה מספר נרות וחילק אותם לקבוצות.
הוא שם לב לכך:
כאשר סדר את הנרות בזוגות - נשאר נר אחד ללא בן זוג.
כאשר סדר את הנרות בחמישיות - נשארו 2 נרות בודדים.
כאשר סדר את הנרות ברביעיות - נשארו 3 נרות בודדים.
תוכלו לגלות מהו מספר נרות שהוציא דורון מהקופסה?
מעובד מתוך: על כנפי האגדה, הטכניון, פרויקט "מחר 98"
עוד על חנוכה:
פיצוח משחקי מזל בחנוכה - פעילויות ברמות שונות בהסתברות.
ראו גם אוסף עשיר לחידות לחנוכה - אלף אפס
משחקי מזל בחנוכה
תקציר| משחקי מזל בחנוכה| פתרונות
1. משחק הסופגניות
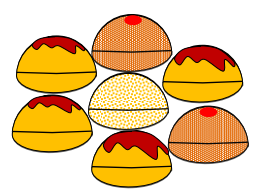
על מגש עגול מונחות 7 סופגניות בטעמים שונים:
4 ממולאות בשוקולד, 2 עם ריבה ואחת ריקה.
הסופגניות משיקות זו לזו ומסודרות במבנה של פרח.
במשחק הסופגניות בחנוכה, מחליפים את המקום של הסופגניות באופן אקראי בכל משחקון, בדומה לכיסאות מוסיקליים.
אם שתי הסופגניות עם הריבה משיקות זו לזו - ניצחתם במשחקון!
שחקו במשחק בעזרת הדפים הבאים ובדקו:
א. שחקו משחק אחד, האם ניצחתם?
ב. שחקו 10 משחקונים. בכמה משחקונים ניצחתם? נסו גם 20 ו-50 משחקים.
ג. מה הסיכוי לנצח ב-100 משחקונים? הסבירו.
מעובד לפי Nrich.math.org
2. משחק הסביבונים
במשחק הסביבונים מסובבים שני סביבונים: האחד סביבון חנוכה שעל ארבע פאותיו רשומות האותיות: נ, ג, ה, פ (נס גדול היה פה).
הסביבון השני הוא משושה שעל שש פאותיו המספרים מ-1 עד 6.
במשחק מוסכם כי נ=1, ג=2, ה=3, פ=4.
יש באפשרותך לבחור באחד מהמשחקים הבאים:
א. זכייה כאשר סכום המספרים בשני הסביבונים שווה ל-7.
ב. זכייה כאשר סכום המספרים בשני הסביבונים הוא לפחות 7.
ג. זכייה כאשר מכפלת המספרים בשני הסביבונים היא לפחות 16.
באיזה משחק כדאי לך לבחור?
מעובד לפי אלכס קופרמן, סטטיסטיקה והסתברות, הוצאת BAK
3. דמי חנוכה
אביטל קיבלה דמי חנוכה עשרה מטבעות שוקולד עליהן מודפסים הספרות 0 עד 9.
מהי ההסתברות שאביטל תוציא מהקופסה, בצורה אקראית, שלושה מטבעות שניתן להרכיב מהם מספר תלת-ספרתי המתחלק ב-9?
עוד על חנוכה:
פיצוח נוסף חנוכה במספרים - אוסף חידות וחידודים העוסקים בקשרים בין מספרים.
ראו גם אוסף עשיר לחידות לחנוכה - אלף אפס
סדרה הנדסית מתכנסת
תקציר| 
סדרה הנדסית מתכנסת| פתרונות| متوالية هندسية تنازلية متداخلة| حلول
1. ללא מילים
האומנם יתכן שסכום סדרה אינסופית הוא סופי ?
לפניכם שלש הוכחות ללא מילים לנוסחת הסכום של סדרה הנדסית אינסופית יורדת. אנא נמקו.
מתוך: "הוכחות ויזואליות ללא מילים" מאת א. זסלבסקי, ג. ויניצקי, קשר ח"ם
2. הזבוב הטורדן
שני רוכבי אופניים יצאו זה לקראת זה משני ישובים שהמרחק ביניהם 40 ק"מ במהירות של 20 קמ"ש כל אחד. לפני הזינוק ישב לו זבוב טורדן על אפו של אחד מהרוכבים. מיד עם צאתם יצא זבוב ועף במהירות של 50 קמ"ש לעבר הרוכב השני. ברגע שהוא מגיע אליו, הוא הופך את כיוון מעופו, ועף אל הרוכב שממנו יצא. כך ממשיך הזבוב הטורדן במעופו בין הרוכבים, עד לרגעהמפגש, אז הוא נמחץ...
מה אורכו של המסלול שעבר הזבוב?
3. האיור המתכנס
באיור שלפניכם המעגלים והריבועים חוסמים זה את זה ונעשים קטנים יותר ויותר. בכל שלב, צבעו את ארבעת הגזרות שנוצרו מחסימת העיגול בריבוע. נתון כי אורך צלע הריבוע החיצוני 10 ס"מ.
א. מהו השטח הצבוע בשלב השביעי?
ב. מהו שטח הכולל של כל התחומים הצבועים בכחול באיור שלפנינו?
ג. אם נמשיך את התהליך אינסוף פעמים, מה יהיה השטח הצבוע?
4. לוח מטרה גיאומטרי
הוזמנת לשחק בלוח קליעה למטרה גיאומטרי ולו צורת משולש ובו חסומים מעגלים לפי האיור הבא.
מעגל, בעל רדיוס של יחידת אורך אחת, חסום במשולש שווה צלעות. מעגל קטן יותר חסום בכל אחת מזוויות המשולש, כך שהוא משיק למעגל הגדול. מעגלים קטנים יותר ויותר חסומים באופן דומה, עד אינסוף.
מהי ההסתברות שהחץ יפגע בתחום האדום?
קישורים נוספים בנושא סדרה הנדסית יורדת:
פינג פונג מתמטי - רון אהרוני- על"ה 38. המחבר משתף אותנו בחוויית גילוי מתמטי שעבר כנער בחיפוש אחר נוסחא לסכום של סדרה גיאומטרית.
משולשים, מעגלים, חוצי זוויות, זהויות טריגונומטריות,סדרה הנדסית ושאיפה לגבול -מה הקשר? אבי סיגלר - על"ה 36. המאמר מציג תהליך גיאומטרי של יצירת סדרה אינסופית של משולשים חסומים במעגל, אשר שטחיהם, היקפיהם ואורכי המחוגים של המעגלים החסומים בהם שואפים באופן מונוטוני לגבול.
פרוייקט לתלמידים - שגעון נקודת האמצע - מחר 98. הפעילות עוסקת בגילוי של תכונות מצולעים, הנוצרים מחיבור נקודות האמצע של צלעות של מרובעים ושל משולשים. תוך כדי הפעילות עוסקים בתהליך אינסופי של יצירת משולשים המוביל למושג הגבול.
פרוייקט לתלמידים - עקומה פתולוגית - מחר 98. בנייה בעזרת המחשב עקומות פתולוגיות, שהן למעשה הפרקטלים של קוך. בכל העקומות קיים פרדוקס שהיקפן שואף לאינסוף ושטחן חסום.
פרוייקט לתלמידים - האינסוף המסתורי - מחר 98. אוסף של פעילויות שונות המתארות פרדוקסים הקשורים למושג האינסוף ודרכי יישומם
"נוסחת הסכום של סדרה הנדסית" - דורית פטקין, קשר חם. בחומר מובא ייצוג גרפי של סכום איברי סדרה הנדסית סופית שאיברה הראשון הוא 1ומנתה מספר טבעי, ושל סכום איברי סדרה הנדסית אינסופית שאיברה הראשון הוא 1 ומנתה מספר הופכי למספר טבעי.
http://en.wikipedia.org/wiki/Geometric_series
האם 1=0.9999999 ? - מאמר על סדרה הנדסית אינסופית יורדת, באנגלית.
מעגלי ארכימדס
תקציר| מעגלי ארכימדס| פתרונות| دوائر أرخميدس| حلول
ארכימדס (287- 212 לפנה"ס) היה מדען יווני שהגיע לתוצאות מרשימות במתמטיקה, הנדסה ופיסיקה.
ארכימדס חישב את ערך Π בדיוק רב (ראו יישומון ממוחשב), ופיתח נוסחאות לחישוב שטח פנים ונפח של גופים שונים.
אגדות רבות מסופרות על ארכימדס ותגליותיו. הוא חקר את פעולתם של מנופים ומספרים שאמר "תנו לי נקודת אחיזה ואוכל להזיז את כדור הארץ..." מיוחסת לו האמירה "אאוריקה", כאשר גילה באמבטיה את חוק הציפה, חוק ארכימדס.
האגדה גם מספרת שחייל שבא לגייסו לצבא לשם פיתוח נשק, הטיל צל על המעגלים שארכימדס צייר על החול. ארכימדס העיר לו "הסתלק, אל תקלקל לי את המעגל"... והחייל התרגז והרגו.
חלק מעבודותיו תורגמו לערבית, והם הגיעו לאירופה במאה ה-12, אבל רק במאה ה-16 הישגיו של ארכימדס זכו להכרה עולמית.
אל תקלקל לי את המעגל - מאמר באלף אפס.
1. שרשרת הזהב של המלך
סיפור נודע על ארכימדס הוא על כתר הזהב המזוייף. בעקבותיו, המלך היירון השני הכיר בארכימדס גם כבלש המפענח תעלומות באמצעות חכמתו והידע הרב שלו.
אגדה אחרת מספרת על מלך שהזמין מצורף הממלכה שרשרת זהב ונתן בידו חוט זהב בצורה של חצי עיגול. הצורף הציע למלך ארבעה עיצובים שונים לשרשרת. המלך שוב חשד שצורף הממלכה מנסה לרמותו וזימן את יועצווביקשו לבדוק האםאורכי השרשראות שווה לחוט הזהב שהפקיד בידו.
היועץ מיד זהה כי הצורף מנסה לרמות את המלך.
האם תוכלו לאמוד את אורכי השרשראות?
מהי השרשרת הקצרה ביותר?
2. סכין הסנדלרים
השטח המוצל שבאיור הדינאמי מתאר סכין סנדלרים הנקרא ביוונית ארבלוס. (Arbelus) יש המכנים אותו סכין תורכי. ארכימדס היה הראשון שחקר את תכונותיו המתמטיות .
א. הזיזו את הנקודה C שעל קוטר חצי העיגול הגדול בכדי לשנות את צורת הארבלוס. תארו את מבנה הארבלוס.
ב. מהו היחס בין אורך הקשת של חצי המעגל הגדול לבין סכום אורכי הקשתות של המעגלים הפנימיים?
ג. משיק לשני חצאי המעגלים חותך את חצי המעגל הגדול בנקודה D.
בונים מעגל שקוטרו הוא CD.
מצאו את יחס שטח עיגול זה ושטח הארבלוס כאשר :
(1). הנקודה C היא במרכז חצי המעגל הגדול.
(2). הנקודה C מחלקת את הקטע AB ביחס 1:2.
(3). ידוע כי רדיוס חצי המעגל הגדול הוא R, ורדיוס אחד מחצי המעגלים הקטנים הוא r.
למתעניינים - התנסו בפרויקט "הפריזבי של ארכימדס".
בתחרות למתמטיקה לתיכונים בפלורידה, הוענק לכל משתתף פריזבי ועליו היה לחקור את התכונות הגיאומטריות של העיצוב המיוחד, באמצעות תוכנות דינאמיות.
בפרוייקט הנחיות לחקירת הארבלוס, המעגלים התאומים של ארכימדס ושרשרת מעגלי פאפוס.
3. המלחייה של ארכימדס
ארכימדס חקר את צורתה של המלחייה האופיינית לימי יוון, הסלינון, שמתוארת באיור הדינאמי הבא:
הסלינון הופיע לראשונה בספרו של ארכימדס, שנכתב לפני 2200 שנה, בשם "ספר הלֶּמות"
(לֶמָּה- משפט עזר להוכחת משפט אחר).
א. הסבירו כיצד נבנה הסלינון.
ב. לפי הלמה ה-14 של ארכימדס שטחו של הסלינון שווה לשטח המעגל שקוטרו GF. נא הוכיחו.
ג. הסבירו את "ההוכחה ללא מילים" של הלֶמָּה של ארכימדס:
