תקציר| נעלה בחזקה זוגית או אי זוגית

בפעילות זו ניתן להיעזר ביישומון (להורדה)

נחקור את הפונקציה   ונשאל כיצד משפיע n על תכונות הפונקציה.

נתבונן בפונקציה כפונקציה מורכבת:     כאשר   .

 א. שרטטו את הגרף  .

ב. נתונה הפונקציה  .

1) מהו תחום ההגדרה של הפונקציה?

2) מהם תחומי החיוביות והשליליות של הפונקציה?

3) מהן האסימפטוטות המקבילות לצירים של הפונקציה?

4) שרטטו סקיצה לגרף הפונקציה. (השוו עם היישומון- להורדה)

5) על פי הגרף, שערו האם לפונקציה יש נקודות פיתול ? אם כן, כמה?

ג. נתונה הפונקציה  .

כיצד תשתנה הפונקציה    אם נעלה אותה בריבוע?

1) מהו תחום ההגדרה של הפונקציה?

2) מהם תחומי החיוביות והשליליות של הפונקציה?

3) מהן האסימפטוטות המקבילות לצירים של הפונקציה?

4) שרטטו סקיצה לגרף הפונקציה. (השוו עם היישומון- להורדה)

5) על פי הגרף, שערו האם לפונקציה יש נקודות פיתול ? אם כן, כמה?

ד. סכמו במה דומות ובמה שונות הפונקציות  , .

כיצד הדבר בא לידי ביטוי בנגזרות של הפונקציות?

ה. נתונה הפונקציה  .

כיצד תשתנה הפונקציה    אם נעלה אותה בחזקת שלוש?

1) מהו תחום ההגדרה של הפונקציה?

2) מהם תחומי החיוביות והשליליות של הפונקציה?

3) מהן האסימפטוטות המקבילות לצירים של הפונקציה?

4) שרטטו סקיצה לגרף הפונקציה. (השוו עם היישומון- להורדה)

5) על פי הגרף, שערו האם לפונקציה יש נקודות פיתול ? אם כן, כמה? נמקו.

ו. סכמו במה דומות ובמה שונות הפונקציות ,  .
.
כיצד הדבר בא לידי ביטוי בנגזרות של הפונקציות?

 ז. עבור n אי זוגי:

1) מצאו כמה נקודות קיצון (אם יש כאלה) יש לפונקציה?

2) מצאו כמה נקודות פיתול (אם יש כאלה) יש לפונקציה?

3) שרטטו סקיצה לגרף הפונקציה.

ח. עבור n זוגי:

1) מצאו כמה נקודות קיצון (אם יש כאלה) יש לפונקציה?

2) מצאו כמה נקודות פיתול (אם יש כאלה) יש לפונקציה?

3) שרטטו סקיצה לגרף הפונקציה.

ט. בצעו את פעילות החקר גם עבור הרכבת פונקציות נוספות. כגון:

תקציר| על משולשים וקטעים

הנקודה O היא אמצע הקטע TK,OM = OK.

פתחו את היישומון, גררו את הנקודה M.

מה תוכלו לומר על מסלול הנקודה?

א. הוסיפו לסרטוט קטעים (בעזרת הכלי קטע ) כך שיתקבל משולש ΔTMK וחקרו את תכונותיו (תוכלו להיעזר ברמז 1 ביישומון).

נסחו משפט המתאר את תגליתכם והוכיחו אותו.

ב. חקרו מהן תכונותיו של המשולש ΔTMK כאשר:

ג. הוסיפו, באמצעות תיבת הבחירה, קטע OP המקביל ל- MK. 

1. הוכיחו: OP=½MK.

2. פי כמה גדול שטח המשולש ΔTMK משטח המשולש ΔOMP

ד. הוסיפו באמצעות תיבת הבחירה את התיכון OQ למשולש ΔMOK.

1. רשמו שתי תכונות של המרובע MPOQ והוכיחו אותן.

2. איזה מרובע התקבל?

3. האם ניתן להזיז את הנקודה M כך שיתקבל ריבוע?

ה. דנה המשיכה ושיחקה ביישומון שלנו, וקיבלה את האיור הבא:

1. הסבירו כיצד נבנה האיור

2. הציעו שאלות לחקירת תכונות האיור.

הפאי הוא מספר מסתורי, המהלך קסם על מתמטיקאים, מדענים וחובבים רבים, ערכו המקורב - 3.14159. ברחבי העולם נוהגים לחגוג לכבודו את יום הפאי ב-14 למרץ (אותו מקובל לרשום כ- 3.14) החל מהשעה 1:59...

פיצוחים בנושא הפאי ויישומו  

• רשימת הפיצוחים בנושא המעגל
• יום פאי שמח
• מעגלי ארכימדס
• משימה פרחונית
• אוצרות פיתגורס 
• פרוייקט עולמי למדידת היקף כדור הארץ
• עיגולים ומעגלים
• קצרצרים... על היקף כדור הארץ 

חגיגות יום הפאי  

• יום הפאי בתיכון בליך - כתבה מצולמת על חגיגות הפאי בתיכון בליך בהנהגת המורה עמר ויסבלום. כל שנה נערכת תחרות לזכירת הספרות שאחרי הנקודה במספר פאי. ביום הפאי 2017, נקבע שיא בליך חדש ומדהים, ע"י ענבל הכט, ששלפה מהזיכרון שלה 1051 ספרות של המספר פאי! ראו סרטון.
• חגיגות יום הפאי בישיבת "שדה יעקב" - מחוויותיו של מורה, פורסם בעל"ה 35.
• מצגת על המספר פאי - הצעה לפעילות חקר ביום הפאי, הרפתקה מתוקשבת WebQuest. פותח ע”י נורית בנציוני.
• אוסף קישורים ליום הפאי מהמרכז הארצי למורים למתמטיקה בחינוך היסודי.
• יום הפאי בויקיפדיה
• יום הפאי במוזיאון המדע בסן פרנסיסקו, שם החלה המסורת לחגיגות לפני 20 שנה.

תמונות ופוסטרים לכבוד הפאי 

• פוסטר של פאי להורדה והדפסה.
• סדרת פוסטרים של פאי פוסטרים צבעוניים ואמננותיים להדפסה והורדה.
• אוסף תמונות וקריקטורות על פאי בדף הפייסבוק של מרכז המורים

לקרוא על פאי  

• מספר הפלא - רן לוי- אודיסאה (גיליון 1 עמ' 38) - מאמר פופולארי הסוקר את ההסטוריה של פאי.
• ערכים מדויקים של פאי במקורות היהדות - בועז צבאן ודוד גרבר- מספר חזק 3.
• המספר פאי עם מליון ספרות אחרי הנקודה!

סרטים ושירים על הפאי 

• Beuaty of Numbers: Pi - המלצה חמה על סרטון יפהפה, הלוקח אותנו למסע בעקבות המספר פאי והופעותיו בטבע. אפילו יצירת המוסיקה הנעימה מתבססת על המספר פאי בבסיס 12.
• the story of Pi - סרט המציג את נוסחת השטח של המעגל.
• שיר: "היום בו גילו את הפאי".
• עוד שיר המתנגן לפי הספרות של פאי
• ועוד סרטונים רבים בערוץ היוטיוב של מרכז המורים 

יישומונים ואנימציות

• יישומון אינטראקטיבי לאומדן הערך של פאי לפי שיטת ארכימדס של NOVA.
• יישומונים דינאמיים בגאוגברה לאומדן הערך של פאי ולהמחשת מציאת שטח עיגול, מאת מרכז המורים
• Find your Pi Day - מצאו את תאריך יום ההולדת שלכם בתוך המספר פאי, מאת WOLFRAM

תקציר|  המחנה "הכי הכי"| פתרונות| المخيم "الأكبر الأصغر"

1. מסגרות מחבלים
ברשותכם חבל באורך 20 מטרים.

א. עליכם ליצור מסגרת בצורה של מקבילית, בעלת השטח הגדול ביותר.

ב. עליכם ליצור שני ריבועים, כך שסכום שטחי שני הריבועים יהיה הקטן ביותר.

הסבירו את בנייתכם ונמקו.

מקור- דן עמיר, פתרונות אלמנטאריים לבעיות קיצון

2. השער הקטון

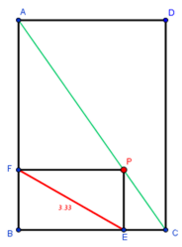
המשימה הבאה היא בניית שער למחנה ע"פ ההוראות הבאות:

המחנה מגודר בצורת מלבן  ABCD.

מקמו נקודה P כלשהי על אלכסון המלבן AC.

מנקודה זו העבירו מקבילים לצלעות המלבן, כך שייווצר מלבן חסום BEPF . המבואה למחנה היא המשולש BFE. 

את השער עליכם לבנות כאלכסון המלבן החסום, FE.

מצאו את מקומה של הנקודה P כך שאורך השער יהיה הקצר ביותר.

מקור- NRICH

תוכלו להעזר ביישומון האינטראקטיבי. 

3. שאבתם מים

הנכם חונים ליד האבן (הנקודה A). משימתכם להביא מים מהנהר אל העץ (הנקודה B).

מהו המסלול הקצר ביותר שבו תוכלו לעשות זאת?

רמז- מה היה הפתרון אם A ו-B נמצאים משני עברי הנהר?

מקור- "משימות לפיתוח חשיבה מתמטית- פרויקט טל"מ - חוג פלוטו"

תוכלו להעזר ביישומון האינטראקטיבי. 

4. השטח הכי גדול

במשימת הישרדות קיבלתם שלוש סנאדות (מוטות עץ) באורכים שונים:  
a<b<c (ראו איור).

עליכם לבנות בעזרת המוטות מרובע, כך ששלושת המוטות יהיו מאונכים זה לזה (טרפז פתוח). באיזה סדר עליכם להניח את המוטות, כך שיתקבל השטח הגדול ביותר?

קישורים למאמרים בנושא:

פתרונות אלמנטאריים לבעיות קיצון: הרצאה של דן עמיר בכנס מורי המתמטיקה בישראל 2005.
הכי טוב שיש: גילה רון ואורית זסלבקי
רשת כבישים מינימלית, אדם קיניסברגר
לא על החשבון הדיפרנציאלי לבדו, אריה רוקח, על"ה 29 
חבית היין של קפלר- פתרון בסביבה של גאומטריה דינאמית, זיוה שחם ובתשבע שכטר, עלה 31
מרובע בעל היקף מינימלי החסום במעגל,  אבי סיגלר, על"ה 24.
Calculus Without Calculus, פתרון בעיות גיאומטריות מחשבון דיפרנציאלי בעזרת גיאומטריה וקטורית פשוטה. 

בבית ספרנו חוגגים את יום הפאי במרוץ מסורתי. 
מגרש בית הספר בנוי ממלבן עליו בנויים שני חצאי מעגלים. המגרש מכיל ששה מסלולי ריצה כל מסלול ברוחב של מטר אחד.

א. אורך המסלול החיצוני הוא 400 מטר. 
רוחב המלבן הוא 100 מטר. (ראו איור).
חשבו את מימדי מגרש בית הספר.

ב. מהו היקף מסלול הריצה הפנימי?

ג. במרוץ הפאי רצים המתחרים 800 מ'.
רוני הגריל את מסלול הריצה החיצוני ואילו חברו הטוב ירדן, קיבל מקום במסלול הפנימי ביותר. 
כולם התכוננו למרוץ ונעמדו בנקודות הזינוק. 
בכמה מטרים קדימה נמצאת נקודת הזינוק של רוני לעומת נקודת הזינוק של ירדן?