המרכז הארצי למורים למתמטיקה בחינוך העל יסודי

מעת לעת אנו שולחים פיצוח, פעילות מתמטית לכיתה, מכיתה ז' ועד יב.
כל הפיצוחים קשורים לתוכניות הלימודים בחט"ב ובחט"ע וניתן לשלבם במהלך ההוראה הן כחיזוק, העשרה והוראה בדרך אחרת.

אתם המורים והתלמידים, מוזמנים לשלוח פתרונות. ואת המיטב שבהם נדאג לפרסם.

תקציר|שלוש פרבולות ולהן שלוש פונקציות קדומות|חומר למורה

לפניכם שלוש פרבולות "מחייכות"

3 parabolas capture

1. שלוש הפרבולות הללו הן נגזרות של פונקציות אחרות כך ש:

$g_{1}^{'}(x)=f_1(x)$ , $g_{2}^{'}(x)=f_2(x)$ , $g_{3}^{'}(x)=f_3(x)$ .

- מהם תחומי העלייה והירידה של הפונקציות?

- סרטטו דוגמאות אפשריות לגרפים של פונקציות $g_{1}$ , $g_{2}$ ו- $g_{3}$ .

- במה דומות ובמה הן שונות?

2. לכל אחת מן הפונקציות חקרו את תחומי הקעירות וציינו את מספר נקודות הפיתול של הפונקציה. הסבירו במה דומות ובמה שונות הפונקציות?

3. לכל אחת מן הפונקציות העריכו את מספר נקודות הפיתול של הפונקציה ואת שיפוע המשיק שם. הסבירו לפיכך במה דומות ובמה שונות הפונקציות?

4. סרטטו 3 פרבולות בעלות מקסימום ואת הפונקציות הקדומות שלהן:

(1) לפרבולה שתי נקודות חיתוך עם ציר ה- x.

(2) לפרבולה נקודת חיתוך אחת עם ציר ה- x.

(3) פרבולה ללא נקודות חיתוך עם ציר ה- x.

5. האם הגרפים של הפונקציות הבאות יכולים לייצג פונקציות ממעלה שלישית? הסבירו.

אם כן, ציינו על הגרף היכן נקודות הפיתול ושרטטו את המשיק שם.

3 parabolas Q5 capture

הפעילות עובדה על פי:
"פונקציה ממעלה שלישית בתמונה משפחתית", ללמוד וללמד אנליזה, פרק 9, ע"מ 209

תקציר|צביעת שני משולשים|חומר למורה

paint two triangels capture נתון משולש ישר זווית ABC שאורך ניצביו הם: 3, 6 ס"מ.

א. נצבע את המשולש החל מקודקוד A, עם משולש ישר זווית דומה לו (ADE) כאשר הנקודה D נעה על הצלע AB.
נסמן את אורך AD=x

הזיזו ביישומון את הנקודה D, ותארו כיצד משתנה השטח הצבוע כאשר x משתנה.

נגדיר פונקציה S(x) המתאימה ל- x את השטח הצבוע. האם פונקציית השטח הצבוע עולה? תארו את קצב ההשתנות שלה.

ב. באותה עת, נצבע משולש ישר זווית חופף 'A'B'C.

נצבע את המשולש החל מקודקוד B', עם טרפז (B'C'LK) כאשר הנקודה K נעה על הצלע A''B.

נסמן את אורך B'K'=x

הזיזו ביישומון את הנקודה D, ותארו כיצד הפעם משתנה השטח הצבוע כאשר x משתנה.
האם פונקציית השטח הצבוע עולה? תארו את קצב ההשתנות שלה.

ג. תארו מתי השטחים הצבועים בשני המשולשים יהיו שווים.

ד. חשבו את השטחים הצבועים בשני המשולשים, כאשר D אמצע הקטע AB ,
ו- K אמצע הקטע A'B' .

ה. חשבו את השטחים הצבועים בשני המשולשים, כאשר X=2.

ו. היעזרו ביישומון לשם חישוב השטחים ומלאו את הטבלה:

X=6	X=5	X=4	X=3	X=2	X=1	X=0
							שטח צבוע במשולש 1
							שטח צבוע במשולש 2

ז. עקבו ביישומון אחר בניית הגרף המתאר את השתנות השטח הצבוע כפונקציה של x, בכל אחד מהמשולשים.
במה דומים ובמה שונים שני הגרפים?

ח. שערו כיצד נראה גרף הנגזרת של פונקצית השטח בכל אחד מהמקרים?

ט. רשמו פונקציה המתארת את השתנות השטח הצבוע כאשר x משתנה עבור כל אחד מהמשולשים. הקלידו בחלון הקלט ובדקו תשובתכם.

גזרו את הפונקציה ובדקו השערתכם.

תקציר| היכן לקנות את הפיצה?|חומר למורה

pizza capture

1. בפסטיבל מדברי גדול התמקמו שתי פיצריות במרחק 6 ק"מ זו מזו, והן מספקות על גמלים פיצות לכל דורש. הפיצריות זהות בתפריט, באיכות ובמחיר הפיצה, וכל אחת מהפיצריות גובה שקל אחד לק"מ דמי משלוח.

א. היכן תקנו את הפיצה (התייחסו למקומות שונים בהם אתם יכולים להימצא?

ב. היכן נמצא קו פרשת הפיצה – קו התפר בין האזור שבו עדיף לקנות מפיצרייה א לבין האזור בו עדיף לקנות מפיצרייה ב?

ג. תוכלו לחקור את הבעיה באמצעות היישומון היכן לקנות את הפיצה. קבעו את יחס המחירים בין הפיצריות ל- m=1. תוכלו להגדיל ולהקטין את המרחק מהפיצרייה השנייה ( $P_2$ ). כדי לראות היכן נמצאות כל נקודות החיתוך בין העגלים, השתמשו באופציה "הפעל עקבות".

2. כיצד ישתנה קו התפר בין אזורי השיווק של הפיצריות, אם פיצרייה א תמשיך לגבות 1 ₪ לק"מ דמי משלוח ואילו פיצרייה ב תעלה את דמי המשלוח ותגבה 2 ₪ לק"מ דמי משלוח?

כדי לחקור אפשרות זו שנו את היחס בין מחירי המשלוח ל- m=2. בהתאם ישתנה גם היחס בין הרדיוסים של המעגלים (מדוע?)

3. אתם מוכנים להמשיך ולחקור את הבעיה לכל בין דמי המשלוח, וכן למצוא את הפתרונות גם בדרך אלגברית. לנוחיותכם, וכדי שהפתרון שלכם יתאים ליישומון, מקמו את הפיצרייה המשנה מחירים בראשית הצירים, ואת הפיצריה הגובה שקל אחד לק"מ מקמו בנקודה (6,0).

תקציר|גלו את ההוכחה|חומר למורה

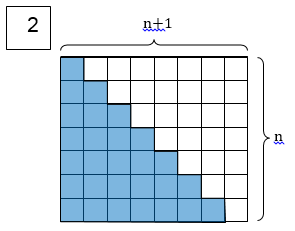
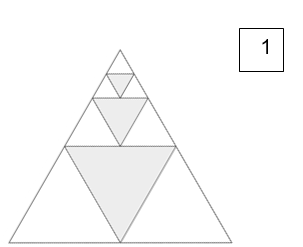
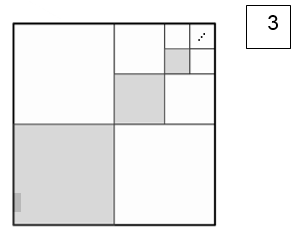
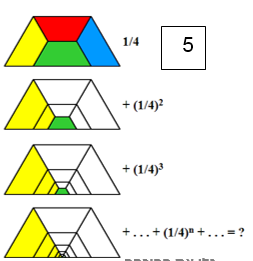
בכל אחד מן הסרטוטים מסתתרת הוכחה לנוסחה הקשורה לסכומי סדרות.

גלו את ההוכחה המסתתרת בכל סרטוט.

$\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\cdot \cdot \cdot =...$

$1+2+3+\cdot \cdot \cdot+n=$

$\frac{1}{4}+\frac{1}{16}+\frac{1}{64}+\cdot \cdot \cdot=...$

בדיוק או בערך

בחרו את התשובה המדויקת ביותר בעיניכם

1. $\frac{1}{4}+\frac{1}{16}+\frac{1}{64}+\cdot \cdot \cdot=...$

א. $\frac{1}{3}$ . ב. קצת יותר מ- $\frac{1}{3}$ . ג. . קצת פחות מ- $\frac{1}{3}$ . ד. מתלבט/ת

2. $0.9+0.09+0.009+...=0.999...=$

א. 1. ב. קצת יותר מ- 1. ג. קצת פחות מ- 1 . ד. מתלבט/ת.

תקציר| pdf מלבן ופרבולה| pdf מדריך למורה

בעקבות מבחן מפמ"ר תשע"ז

rectangle and parabula Q

במערכת הצירים מסורטטים שני גרפים של פונקציות ריבועיות.
גרף אחד הוא של הפונקציה f(x) = x2 (מסומן ב-i ).

1. מי מבין הפונקציות הבאות לא יכולה להיות הפונקציה שהגרף שלה מסומן ב- ii? הסבירו. (יש יותר מאשר תשובה נכונה אחת)

rectangle and parabula capture (1) $g(x)=2x^2$

(2) $g(x)=x^2+4$

(3) $g(x)=3x^2$

(4) $g(x)=x^2-2$

(5) $g(x)=x^2+6$

(6) $g(x)=(x+2)^2$

2. נתון גם שהגרף המסומן ב- (ii) מתקבל מהגרף המסומן ב- (i) על ידי הזזה 4 יחידות למעלה.

א. מהם שיעורי נקודת הקדקוד של הפרבולה המסומנת ב- ii?

ב. כתבו את הביטוי האלגברי של הפרבולה המסומנת ((ii.

3. סרטטו מלבן שאחד מקדקודיו הוא ראשית הצירים וקדקוד נגדי לו הוא M(2,4). צלע אחת של המלבן על ציר ה- y (ראו סרטוט).

א. הסבירו מדוע נובע מהנתונים שלמלבן יש גם צלע המונחת על ציר ה- x.

ב. חשבו את שטח המלבן. הציגו דרך פתרון.

ג. איזו מבין המשוואות מתאימה לייצג את הישר
עליו מונח אחד מאלכסוני המלבן.

(1)y = 2x + 4 (2) y = –2x + 4
(3) y = x + 4 (4) y = –x + 4.

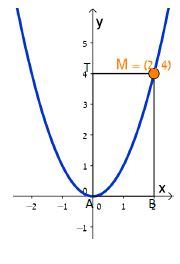
4. עדן בנתה (אפשר בעזרת היישומון) מלבנים נוספים ABMP, שאחד מקדקודיהם, M, נמצא על הפרבולה $y=x^2$ , ושני קדקודים שלהם על הצירים (ראו סרטוט).

bike and bicycle Q4

השלימו בטבלה מה שטח המלבן של כל אחד מהמלבנים שיצרה עדן.

		(3,__)	(2,4)	(1,1)	הנקודה M
			8 סמ"ר	1 סמ"ר	שטח המלבן

5. עדן שמה לב ששטח כל אחד מהם הוא $AB^3$ , כאשר $AB$ אורך הצלע המונחת על ציר ה- x. למשל: אם הקדקוד M הוא בנקודה (3,9), אורך הצלע $AB$ הוא 3 יחידות ושטח המלבן 27 יחידות. האם זה מקרי? הסבירו תוכלו להיעזר ביישומון.

6. עופר ואלון בנו מלבן שקדקוד אחד שלו על הפרבולה $y=x^2+4$ ,שתי צלעות שלו על הצירים ושתי צלעות מקבילות לצירים. הם סימנו ב- $x$ את הצלע המונחת על ציר ה- $x$ , וחיפשו ביטוי אלגברי לשטח המלבן כפונקציה של $x$ . עופר קיבל את הביטוי $x(x^2+4)$ , אלון קיבל את הביטוי $x^3+4x$ .

א. מי צודק? האם ייתכן ששניהם צודקים?

ב. כיצד חישב כל אחד מהם את שטח המלבן?

7. גם יעל בנתה מלבן עבור הפרבולה המוזזת $y=x^2+4$ , כאשר קדקוד אחד שלו על הפרבולה $y=x^2+4$ , שתי צלעות שלו על הצירים ושתי צלעות נוספות מקבילות לצירים. יעל חילקה אותו לשני מלבנים באופן שונה מאשר אלון.

סמנו ב- $x$ את הצלע המונחת על ציר ה- $x$ .

ניתן להיעזר ביישומון מלבן ופרבולה מוזזת.

א. הביעו בעזרת $x$ , את אורכי הצלעות של המלבן ABCD ואת שטחו.

ב. הביעו בעזרת $x$ , את אורכי הצלעות של המלבן PMCD ואת שטחו.

ג. הסבירו כיצד ניתן להביע את שטח המלבן של הפונקציה המוזזת ((ABCD כסכום שני מלבנים.

ד. האם קיים שוויון בין הביטויים שקיבלתם בסעיף א' לסעיף ג'? הסבירו שיקולכם.

עמוד 3 מתוך 28

thumbnail logos