תקציר| לרבע את הירח

אחת הבעיות שהעסיקו את המתמטיקאים מאות בשנים, היתה כיצד ניתן "לרבע" את המעגל, כלומר כיצד ניתן לבנות בעזרת סרגל ומחוגה ריבוע ששטחו כשטח מעגל נתון. בניסיונתיהם הרבים, ניסו גם לרבע צורות מעגליות כגון סהרונים.

"סהרון" היא צורה החסומה על ידי שתי קשתות מעגליות, בדומה לירח.    

1. לרבע את הסהרון של היפוקרטס

א. עקבו ביישומון אחר שלבי הבנייה ותארו במילים כיצד בנה היפוקרטס את הסהרון. רשמו את הנתונים באופן מתמטי.

ב. הראו כי שטח המעגל הקטן שווה לחצי משטח המעגל הגדול.              

ג. מה היחס בין שטח של הסהרון ושטח המשולש ?
חשבו את שטח הסהרון בעזרת חיבור וחיסור שטחים.

ד. בנו ריבוע ששטחו כשטח הסהרון.

2. לרבע את המעגל- האמנם?

היפוקרטוס טען כי "הוכיח" שניתן לרבע את המעגל, (לבנות ריבוע ששטחו שווה לשטח המעגל)

למרות שכיום ידוע שלא ניתן לעשות זאת. במה טעה היפוקרטס?


 

א. הראו כי :  שטח ששת הסהרונים - שטח המשושה = שטח המעגל הקטן היעזרו בחיבור וחיסור שטחים.

ב. משושה, בהיותו מצולע, ניתן לרבע, כלומר לבנות ריבוע בעל שטח שווה. היפורקטס הראה שניתן לרבע סהרונים.
מכאן ניתן להסיק שניתן לרבע את המעגל... האמנם? במה טעה היפורקטס?

3. לרבע את הסהרונים של אלחאסן

אלחאסן סרטט את שני סהרונים באיור הבא בעזרת שלושה חצאי מעגלים.

א. עקבו ביישומון אחר שלבי הבנייה ותארו במילים כיצד בנה את הסהרונים. רשמו את הנתונים באופן מתמטי.

ב. מה היחס בין שטח של שני הסהרונים ושטח המשולש ?

ג. בנו ריבוע ששטחו כשטח שני הסהרונים.

מקורות נוספים:

מי הפך את הירח לריבוע? – עטרה שריקי, קשר ח"ם

מצגת "לרבע את המעגל", רקע היסטורי ומתמטי. (באנגלית)

תקציר|  דלתוני ריצוף| לדפי גזירה| פתרונות והנחיות

1. פירוק והרכבה של משולש שווה-צלעות

לפניכם משולש שווה צלעות. כידוע גובה במשולש שווה-צלעות מחלק אותו לשני משולשים חופפים. (מדוע?)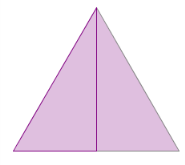  

גזרו משולש שווה צלעות והרכיבו מחדש את שני המשולשים על ידי הצמדת שני קדקודים של משולש אחד לשני קדקודים של המשולש השני.

כמה מצולעים שונים תוכלו להרכיב בדרך זו?

2. דלתון הריצוף

אחת הצורות שניתן ליצור באמצעות הצמדת המשולשים היא דלתון. 

דלתונים מיוחדים אלה נקראים דלתוני-ריצוף בגלל האפשרות ליצור

בעזרתם ריצופים של צורות גאומטריות רבות ואף של המישור כולו.

א. מהן התכונות המיוחדות של דלתונים אלה?

1. מהן מידות הזויות של דתלוני-ריצוף?
2. מצאו קשרים בין אורכי האלכסונים של הדלתון לבין אורכי הצלעות.

ב. גזרו מדפי הגזירה מספר דלתונים ונסו להרכיב באמצעותם מצולעים שונים, כך שדלתוני הריצוף נצמדים לאורך צלע שלמה.

1. אילו מהצורות הבאות ניתן להרכיב משולש, מרובע, מחומש, משושה?
2. אילו מצולעים משוכללים הצלחתם לבנות? הסבירו כיצד.

נסו להרכיב את המצולעים ביותר מאשר דרך אחת.

ג. הציעו דרכים שונות לרצף משטח בעזרת דלתוני הריצוף.

3. משושים

בבית הספר “חופים” יש חצרות פנימיות בצורת משושה. במסגרת פרוייקט לשיפור פני בית הספר עלתה הצעה
ליצור משטחים משושים באמצעות אריחי קרמיקה בצורת דלתוני ריצוף .

בקטלוג הגלריה לאריחים מצאו את הדגם שבתמונה וניסו לברר:

א. פי כמה גדול היקף המשושה החיצוני מהיקף המשושה הפנימי?
פי כמה גדול השטח?

ב. האם ניתן לבנות את ריצוף הקרמיקה באמצעות אריחים בשני צבעים בלבד, מבלי שלאריחים באותו צבע תהיה צלע משותפת?

ג. האם ניתן לבנות את ריצוף הקרמיקה באמצעות אריחים בשלושה צבעים בלבד מבלי שלאריחים באותו צבע תהיה צלע משותפת?

ד. האם ניתן להמשיך את הריצוף ולקבל משושה עוד יותר גדול הבנוי מאותם האריחים?
לכמה אריחים נוספים תזדקקו?

 4. ריצוף באריחים בשני גדלים

לפניכם שני אריחים לריצוף. שני דלתוני ריצוף כך שהצלע הקצרה בדלתון הגדול שווה באורכה לצלע הארוכה בדלתון הקטן.

א. מה יחס ההיקפים בין שני הדלתונים? מהו יחס השטחים?

ב. הצמידו את שני אריחי הדלתונים זה לזה. איזה מרובע התקבל? תארו תכונותיו.

ג. נסו להרכיב מצולעים שונים מדלתוני ריצוף אלו.

ד. האם ניתן לבנות דלתון ריצוף דומה גדול יותר המורכב משני אריחים אלו?

5. ריצוף באריחים בגדלים משתנים

תלמידי מגמת האמנות רוצים ליצור עיטור מיוחד לקיר מבנה המגמה בעזרת דלתוני ריצוף.
בהצעה ניתן להשתמש בגדלים שונים של דלתוני ריצוף.

התקבלו שתי הצעות:
הקבוצה של חן הציעה לבנות עיטור של פרח, והקבוצה של נוי הציעה לבנות עיטור משושה.

א. תארו את בניית הריצוף בכל אחת מההצעות.

ב. תכננו (בשרטוט או במילים) כיצד ניתן להוסיף שכבה נוספת לכל אחד מהעיטורים. לכמה דלתונים תזדקקו להוספת שכבה?

בעת שקילת ההצעה יש לבדוק בכל אחד מהעיטורים:

א. האם קיים יחס קבוע בין היקפי השכבות ?

ב. פי כמה גדול שטח האריחים הסגולים משטח האריחים בתכלת ?

ג. האם נוכל להגדיל את העיטור על ידי הוספת שכבות של דלתוני ריצוף?

ד. האם נוכל להוסיף שכבות נוספות של דלתוני ריצוף גם כלפי פנים?

ה. האם נוכל באופן זה למלא את כל השטח הלא מרוצף?

ו.  האם ניתן למלא את כל השטח הפנימי בדלתוני ריצוף בדרך אחרת?

קישורים 

דלתוני ריצוף בויקיפדיה

עוד ריצופי דלתונים בבלוג math humbre

היצירה Fractal Tessellation of Spirals שלהאמן Robert Fathauer מבוססת על דלתוני ריצוף

• טרנסיטיביות
• תורת המשחקים

תקציר | על מתמטיקה ודמוקרטיה| פתרונות

1. החלטה גורלית

בית ספר "עלומים" נקלע לקשיים כלכליים, וההנהלה נאלצה להודיע על קיצוצים בתקציב.

מועצת התלמידים המודאגת התגייסה כדי לסייע להחלץ מהמשבר, וכינסה את כל תלמידי השכבה הבוגרת לישיבת חירום

והציעה שלוש הצעות:

    א. לוותר על תקציב מסיבת סוף השנה ולגייס כספים באירוע התרמה לשכבה הצעירה.

    ב. קיצור הטיול השנתי  ביום ובמקומו לצאת ליום עבודה בחקלאות כתרומה לבית הספר.

    ג.  צמצום שירותי הנקיון בבית הספר ויצירת תורנות ניקיון של התלמידים.

לקראת ההצבעה, לאחר דיון סוער, יודעים כל המשתתפים בדיון את סדרי העדיפות של חבריהם.

יושב ראש מועצת התלמידים מתאר את התמונה הבאה:

- מרבית החברים מעדיפים את הצעה א על הצעה ב

- מרבית החברים מעדיפים את הצעה ב על הצעה ג

- מרבית החברים מעדיפים את הצעה ג על הצעה א.

האם מצב זה ייתכן? הסבירו.

2. בחירות למועצת תלמידים

בבית הספר "עלומים" מקיימים כל שנה בחירות למועצת התלמידים.

על פי חוקי בית הספר כל תלמיד יכול להציע את מועמדותו למועצת התלמידים. כל תלמיד שם בקלפי פתק עם שם אחד.

אם יש תלמיד שזכה ב- 40% מהקולות הכשרים או יותר , אז התלמיד שזכה במספר הקולות הגדול ביותר נבחר לראשות מועצת התלמידים.

אם אף אחד מהתלמידים לא זכה ב- 40% מהקולות הכשרים או יותר נערך סיבוב שני בו מתמודדים שני המועמדים שזכו במירב הקולות.

אלה מתן וגל מציגים את מועמדותם לראשות מועצת התלמידים.

    א. כמה אפשרויות לסדר עדיפות בין המועמדים קיימות?
 

    ב. לאחר חודש של תעמולת בחירות יודע כל אחד מתלמידי בית הספר את סדרי העדיפויות של כל אחד מחבריו:

96 תלמידים מחזיקים בסדר העדיפויות:  אלה  >  מתן  >  גל

110 תלמידים מחזיקים בסדר העדיפויות: מתן   >  גל    >  אלה

95 תלמידים מחזיקים בסדר העדיפויות: גל   >  אלה >  מתן

20 תלמידים מחזיקים בסדר העדיפויות: אלה  >  גל    >  מתן

20 תלמידים מחזיקים בסדר העדיפויות: מתן  >  אלה  >  גל

20 תלמידים מחזיקים בסדר העדיפויות: גל    > מתן    >  אלה

אם כל אחד יצביע על פי העדפותיו:  

  1. האם יהיה סיבוב בחירות שני?

  2. מי יהיה ראש מועצת התלמידים?


  3. המועמד מתן צופה את תוצאות הבחירות מראש. הוא וחברתו נועה מחליטים להצביע בעד גל (במקום בעד מתן).
 

האם החלטתם יכולה להשפיע על תוצאות הבחירות? הסבירו.

קישורים נוספים:

• דמוקרטיה מנקודת המבט של מתמטיקה– חומר לעבודות מחקר – ד"ר פיטר סמובול על שיטות בחירה שונות ופרדוקסים של בחירות.
• דמוקרטיה במספרים – שיעור באזרחות מאת מטח. עיבוד ניתוח של סקר המוצג בתמונות, אינפוגרפיקה. שימוש בתוכנת  Thinglink המאפשרת הוספת "נקודות חמות" על גבי תמונות.
• מקימים קואליציה (סימולציה) - הצעה לפעילות בכיתה בנושא הקמת הקואליציה בישראל בעקבות תוצאות הבחירות לכנסת ה-19. הפעילות מתבססת על סימולציה המבוססת על קובץ אקסל.
• בחירות רבותיי, בחירות – מכון דוידסון - בסדרת הכתבות נדבר על סקרי הבחירות, על ההסכמים שיוצר אחוז החסימה, על הקשר של הבחירות לתורת המשחקים ועוד.
• המתמטיקה של הדמוקרטיה – מאמר דיעה מתוך הבלוג – למה ללמוד מתמטיקה