- עמוד הבית
- מדורי המרכז
- פיצוחים
- במבט נוסף
אלגברה וחדו"א
השוואת משולשים דומים
מקור: brilliant.
נושא: גאומטריה, דמיון משולשים.
משולש ABC דומה למשולש DCE
DC || AB
אם השטח של משולש ABC הוא 36 יח"ר והשטח של משולש CDE הוא 9 יח"ר
מה יהיה השטח של משולש ACD?
כיתות: ח'-י'.
- פרטים
- קטגוריה: מתנות קטנות
הסתברות בקופסה
מקור: brilliant
נושא: הסתברות
בקופסה A יש 2 כדורים אדומים וכדור אחד לבן
בקופסה B יש 3 כדורים אדומים ו-2 כדרים לבנים.
אם באופן אקראי בוחרים קופסה ובאופן אקראי מוציאים כדור והוא כדור לבן
מה ההסתברות שהקופסה שנבחרה היא קופסה A?
- פרטים
- קטגוריה: מתנות קטנות
תרגיל בשורשים
מקור: Brilliant
נושא: אלגברה, נוסחאות הכפל המקוצר
כיתות: ט- יא
- פרטים
- קטגוריה: מתנות קטנות
רופאים באחוזים
מקור: Brilliant
נושא: אחוזים
כיתות: ח'-ט'
בחדר יש 100 אנשים , 99% מהם רופאים.
כמה רופאים צריכים לעזוב את החדר כדי שבחדר יהיו בדיוק 98% רופאים?
- פרטים
- קטגוריה: מתנות קטנות
עוגת היומולדת
מקור: Alex Bellos's Monday puzzle
כיתה: ז-יב.
חידה "עוגת היומולדת" פורסמה בפייסבוק וזכתה להדים רבים, ואף ליישומון מרהיב מאת עידן טל. נשמח לקבל פתרונות שונים של תלמידים ונפרסמם.
- פרטים
- קטגוריה: מתנות קטנות
דמיין את התופעה
מקור: Underground Mathematics
כיתה: ט' – יב'
תרגום של פעילות ובה מספר היגדים המתארים תופעות ותהליכים שונים מחיי היום יום. יש להתאים גרף וביטוי אלגברי כמודל מתמטי לכל אחד מההיגדים.
תרגום הפעילות לחידון אינטראקטיבי מאת מט"ח
- פרטים
- קטגוריה: מתנות קטנות
זווית בין תיכונים
מקור: Brilliant
נושא: גיאומטריה – מפגש תיכונים
כיתות: ט'-יא'
הנקודה G היא מפגש התיכונים במשולש ABC
AG = BC
חשבו את זווית ,BGCהציעו יותר מדרך פתרון אחת.
מינוף השאלה לשאלון 807: (בהצעת סוהיל שריף)
במשולש ABC הנקודה Gהיא נקודת חיתוך התיכונים ומתקיים כי : . AG=BCמצא את המקום הגיאומטרי של אוסף הנקודות G המתקבלות באופן זה.
- פרטים
- קטגוריה: מתנות קטנות
כפול זה בזה
מקור: Brilliant
נושא: אלגברה– פתרון מערכת משוואות
כיתות: ט'-י'
יש דרך מהירה לפתור בעיות כאלה:
נתון ש- m, a, t, h, הם מספרים ממשיים שפותרים את המשוואות שלעיל.
מצאו את הערך של m x a x t x h
המלצה מחודשת לחוברת "מה ערך המערך" שנכתבה במרכז המורים עבור תלמידי עמ"ט
- פרטים
- קטגוריה: מתנות קטנות
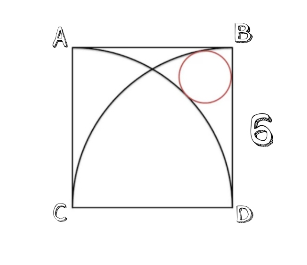
העיגול הקטן
מקור: Brilliant
נושא: גיאומטריה – המעגל, משיקים, פיתגורס
כיתות: י'-יא'
מומלץ לעיין גם במאמר מתוך על"ה : על מעגלים משיקים ומספרי פיבונצ'י/ אסתר גרונהט ולוי ינובסקי
המרובע ABCD הוא ריבוע שאורך צלעו 6 יחי'.
חשבו את הרדיוס של העיגול הקטן.
- פרטים
- קטגוריה: מתנות קטנות
משוואה מעריכית שכזו
מקור: Brilliant
נושא: אלגברה – משוואות מעריכיות
כיתות: ט'-י'
מה הסכום של כל הערכים השלמים של x עבור
פרטים והנחות:
x יכול להיות שלילי. משום שהמעריך הוא שלם, הערך יכול להיות מוגדר.
- פרטים
- קטגוריה: מתנות קטנות
