האורים והתומים של הלוגריתמים

האורים והתומים של הלוגריתמים

תקציר |  לוגריתמים |  בערבית

נאפייר (1552-1632) היה מתמטיקאי חובב מסקוטלנד אשר חיפש דרכים לבצע חישובים מורכבים ועם מספרים גדולים בצורה פשוטה. 

אחד התחומים שעניינו במיוחד את נאפייר היתה האסטרונומיה, אך המחשבה על החישובים האינסופיים הנדרשים מאסטרונומים גרמה לו לאנחות. לאחר 20 שנות לימוד וניסויים, הציג נאפייר את השימוש בלוגריתמים - פריצת דרך שלא תאמן בפישוט החישוב. תגלית זו התקבלה בכל רחבי העולם בתרועה ובהסכמה, לא רק על ידי אסטרונומים, אלא גם על ידי אנשים שחישובים מגושמים הכבידו עליהם. לוגריתמים, העיקרון שעליו מבוסס סרגל החישוב, ביטלו למעשה את הצורך בכפל וחילוק ואפשרו להסתפק בחיבור וחיסור.

מקור- גלים

נאפייר גילה כי קיים קשר בין שתי סדרות מוכרות היטב: הסדרה ההנדסית והסדרה החשבונית.
הוא גילה שניתן לכתוב סדרה אחת באמצעות השנייה דבר שסייע לו לבצע במהירות חישוב של תרגילי כפל של מספרים גדולים.

 1. נתבונן בשתי הסדרות הבאות:

א. בחרו שני מספרים מהסדרה ההנדסית והכפילו אותם. לדוגמה: 8x32 = 256
    סכמו את המספרים המתאימים בסדרה החשבונית. 3+5 = 8
    מה תוכלו לומר על הקשר בין התוצאות?
ב. נסו שוב להכפיל זוג מספרים אחר מהסדרה ההנדסית. האם גם הפעם זה עבד?
ג. המשיכו את שתי הסדרות וכפלו בדרך המהירה של נאפייר. חשבו 256*1024.
ד. חשבו באמצעות הטבלה, מהו הממוצע הגיאומטרי של 8 ו- 32?
ה. חשבו במהירות, מהו הממוצע הגיאומטרי של 8, 32, 128, 512?
ו. כיצד נוכל לחשב תרגילי חילוק במהירות? 1024:128=?

ז. רשמו את הקשרים שמצאתם בטבלה בעזרת לוגריתמים.
    למשל:

ח. נסחו כלל לסכום של שני לוגריתמים בבסיס 2. באופן דומה נסחו כלל לחיסור.

2. נתבונן בטבלה הבאה של לוגריתמים בבסיס עשר. שימו לב כי הסדרה החשבונית הורחבה.

א. בדקו האם התכונות שמצאתם בסעיף הקודם מתקיימות גם עבור הסדרות הללו.
ב. מקובל להשמיט את הבסיס 10 בכתיבת לוגריתמים בבסיס 10.
חשבו לפי הטבלה:

ג. בטבלה הבאה שונתה הסדרה החשבונית. השלימו את הטבלה עבור הסדרה ההנדסית.

 ד. חשבו לפי הטבלה ולפי החוקים שמצאתם:

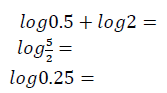
ה. נאפייר ועמיתיו מצאו דרך לקשר ביו סדרות חשבוניות וגאומטריות, ובנו טבלאות לוגריתמיים לשם הקלה בחישובים.
נסחו את הקשר בין הסדרה ההנדסית לסדרה החשבונית.
האם מתקיים קשר זה בכל שתי סדרות חשבוניות והנדסיות?

מקורות נוספים:
סרגל לוגריתמי - פעילות של NCTM
The Oughtred Society - אגודה של אספני סרגלי חישוב, הסבר על פעולתם ועל ההיסטוריה שלהם.
Slide Rules and Logarithm Tables - Mathematical intention 

פי כמה רעידת האדמה בהאיטי הייתה חזקה מרעידת האדמה באילת?

סולם ריכטר - פותח ב 1935 ע"י מדען אמריקאי ששמו צ'ארלס ריכטר. ריכטר פיתח מודל מתמטי להשוואה בין עוצמות של רעידות אדמה. סולם זה מציג ערך כמותי ומודד את העוצמה של רעידת האדמה לפי כמות האנרגיה שהשתחררה לפי גודל התנודות שנרשמו ושנקלטו ע"י הסיסמוגרף. מדובר על סולם מדידה לוגריתמי וכל דרגה בו מעידה על עוצמה חזקה פי 10 מקודמתה. 
דרגות 4 - 1 - רעשים קלים כמעט לא מורגשים;
דרגות 8 - 5 - רעשים מסוכנים עד הרסניים;
דרגות 12 - 9 - הרסניים ביותר.

לסולם ריכטר אין ערך עליון. בצ'ילה בשנת 1960 היתה רעידת אדמה החזקה ביותר שידועה עד כה בעוצמה 9.5 בסולם ריכטר. סדר הגודל של רעידת האדמה (R) הוא פונקציה של עוצמתה (I) והעוצמה המינימלית

1. נחשב את העוצמה של רעידת האדמה באילת אשר נמדדה 4.5 בסולם ריכטר.
    
   חשבו באופן דומה את עוצמת רעידת האדמה בהאיטי אשר נמדדה 7 בסולם ריכטר.
   פי כמה רעידת האדמה בהאיטי הייתה חזקה מרעידת האדמה באילת?
2. בשנת 1837 אירעה בארץ רעידת אדמה, שנמדדה 6 בסולם ריכטר, אשר הרסה את צפת וטבריה וגרמה להרוגים רבים והרס רב.
   חשבו פי כמה רעידת האדמה בהאיטי הייתה חזקה מרעידת האדמה בצפת ובטבריה?
3. ידוע שרעידת אדמה מלווה ברעידות אדמה עוקבות. לאחר הרעש בהאיטי התרחשה רעידה נוספת שהייתה קטנה בעוצמתה פי 100 מהרעידה המקורית. באיזו רמה של סולם ריכטר נמדדה רעידה זו? ולאחריה רעידה נוספת שהייתה קטנה פי 3160 לערך? באיזו רמה של סולם ריכטר נמדדה רעידה זו?
   
   

1. האם יתכן ש- 2>3?
   
   
   
2. טעות בספר?
   פתרתי את המשוואה באופן הבא:

הסתכלתי בפתרונות הספר, אך להפתעתי מצאתי שם ארבעה פתרונות:

תוכלו לעזור לי לדעת מי צודק?

מקור - תבלינים מתמטיים, לעשות מתמטיקה - הטכניון.

פעילויות נוספות בנושא הלוגריתמים:

• החיפוש אחר המספר המופלא e
• הפוך על הפוך
• logaⁿ=n loga לא נכון (לא תמיד נכון) - אריה רוקח, על"ה 14.