תקציר| ממוצעי פיתגורס ועוד| פתרון| حلول

האגדה מספרת שפיתגורס, המתמטיקאי היווני הנודע מימי יוון הקדומה ( 500 לפנה"ס), עבר פעם ליד חרש ברזל והתאהב בצלילי דפיקות הפטיש שהיו נעימים לאוזנו. הוא בדק ומצא, כי משקלי הפטישים היו 6, 8, 9, ו-12 ק"ג. היחסים בין משקלי הפטישים הפיקו צלילים הרמוניים.

 מה מיוחד כל כך במספרים אלה? שאל.

הוא מצא כי הממוצע החשבוני בין 6 ל-12 הוא   

ואילו הממוצע ההרמוני בין 6 ל-12 הוא   

פיתגורס בדק גם כלי פריטה וגילה שקיים קשר מתמטי בין אורך המיתר, שעליו פורטים, ובין גובה הצליל: כשמתקיים יחס מסוים בין אורכי המיתרים, נוצרת הרמוניה בין הצלילים. כך הפך פיתגורס לראשון שהראה כי יש קשר הדוק בין מדע מדויק לבין מוסיקה.

1. מהירות ממוצעת

א. לטיול השנתי נסענו באוטובוס בכביש המהיר. בשל עומס כבד בתנועה נסע האוטובוס לאיטו במהירות של 40 קמ"ש חצי מהדרך. ובחצי השני של הדרך הצליח להגביר את מהירותו ל-80 קמ"ש. האם מהירותו הממוצעת בדרך כולה הייתה 60 קמ"ש? יותר, או פחות?

ב. באיזו מהירות היה צריך האוטובוס לנסוע בחצי הדרך השנייה בכדי שמהירותו הממוצעת תהיה 80 קמ"ש?

ג. מכונית עברה דרך של 40 ק"מ במהירות ממוצעת של 40 קמ"ש. מה צריכה להיות מהירותה הממוצעת ב-40 הק"מ הבאים כדי שמהירותה הממוצעת לאורך כל 80 הק"מ תהיה 80 קמ"ש?

2. ממוצעים בין מלבן וריבוע

נתון מלבן שמידותיו x ו-y. נשאל את עצמנו שאלות אחדות:

א. מה צריך להיות אורך צלע הריבוע שהיקפו ישווה להיקף המלבן?

ב. מה צריך להיות אורך צלע הריבוע ששטחו ישווה לשטח המלבן?

ג. מה צריך להיות אורך צלע הריבוע שאלכסונו ישווה לאלכסון המלבן?

ד. מה צריך להיות אורך צלע הריבוע שהיחס בין שטחו להיקפו ישווה ליחס בין שטח והיקף המלבן?

הידעתם?

כאשר חוקרים את תפקודם הביולוגי של גופים חיים יש חשיבות עיקרית לא לנפח הגוף בפני עצמו, או לשטח חיצוני של הגוף בפני עצמו, אלא ליחס שבין הנפח לשטח הגוף. באותה מידה בצורות שטוחות יש חשיבות ליחס שבין שטח הצורה להיקפה. למשל, מדינה שקו הגבול שלה ארוך מאוד ביחס לשטחה יש לה בעיות ביטחוניות מסובכות. באיזה ממוצע כדאי להשתמש?

3. מי גדול יותר?

נכיר ארבעה ממוצעים בין שני מספרים a ו- b הנפוצים ביותר. 
שלושת הראשונים נקראים ממוצעי פיתגורס.

א. חשבו את ארבעת הממוצעים השונים בין המספרים 4 ו-12 ובין 9 ו-16. 
סדרו את הממוצעים על פי גודלם. 
בדקו ביישום הדינאמי.

ב. הסבירו על פי האיור הבא מדוע הממוצע החשבוני גדול מן הממוצע הגיאומטרי.

ג. הסבירו על פי היישום הדינאמי מדוע האורכים A, G ו-H הם שלושת ממוצעי פיתגורס של האורכים a ו-b. 
מי גדול ממי?

ד. הוכיחו 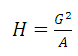כי: 

ה. הוכיחו באיור כי: 

ו. סדרו את ארבעת הממוצעים על פי גודלם.

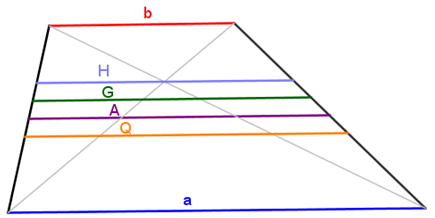4. ארבעה ממוצעים בטרפז

הוכיחו כי:

1. קטע אמצעים בטרפז שווה לממוצע החשבוני של בסיסי הטרפז.

2. קטע מקביל לבסיסי הטרפז המחלק לשני טרפזים דומים שווה לממוצע הגיאומטרי של בסיסי הטרפז.

3. קטע מקביל בטרפז העובר דרך מפגש אלכסוניו שווה לממוצע ההרמוני של בסיסי הטרפז.

4. קטע מקביל לבסיסי הטרפז המחלק לשני טרפזים שווי שטח, שווה לממוצע הריבועי של בסיסי הטרפז.

מקורות והרחבה: 

שלושת הממוצעים – פרופ' אביטל - גליונות לחשבון מס 7

על ממוצעים שונים – פרופ' אביטל – גליונות לחשבון מס 62

ממוצעים ומוסיקה – מייקל נ. פריד – על"ה 30, 2003

שבעה ממוצעים שונים בטרפז – נתן ויזדום - אוניברסיטת ג'ורג'יה

הוכחות ויזואליות ללא מילים (כמעט) - אורית זסלבסקי, גרייסי ויניצקי.