2. מן הפנים אל החוץ
א. נתונות שלוש נקודות A, B, C שהן אמצעי הצלעות של משולש כלשהו, אך המשולש המקורי עצמו
(DEFD) נעלם. בדקו ביישום הדינאמי 
האם וכיצד ניתן ליצור את משולש DEFD:
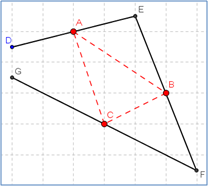- האם תמיד ניתן לבנות את המשולש על פי אמצעי צלעותיו?
- כיצד ניתן לבנות את המשולש המקורי? תארו את הבנייה ונמקו.
- האם קיים רק משולש אחד כזה?
- בהינתן שיעורי נקודות האמצע, התוכלו למצוא את שיעורי קודקודי המשולש המקורי.
ב. נתונות ארבע נקודות A, B, C, D שהן אמצעי הצלעות של מרובע כלשהו, אך המרובע המקורי עצמו
(EFGH) נעלם. בדקו ביישום הדינאמי האם וכיצד ניתן ליצור את המרובע EFGH:
- האם תמיד ניתן לבנות את המרובע על פי אמצעי צלעותיו? אם כן, באיזה תנאי?
- כיצד ניתן לבנות את המרובע המקורי? תארו את הבנייה ונמקו.
- האם קיים רק מרובע אחד כזה?
ג. האם וכיצד ניתן לבנות מחומש מחמש הנקודות של אמצעי הצלעות?
האם וכיצד ניתן לבנות משושה משש הנקודות של אמצעי הצלעות?
